基于 CFD-DEM 耦合的水力旋流器性能预测分析

胡自强，周贤武，吴强波

江西耐普矿机股份有限公司 江西上饶 334200

水 力旋流器作为一种高效分离设备，被应用于石 油化工、选矿和工业除尘等领域，具有占地面积小、分级效率高、操作简便等特点，在选矿行业主要用于矿物颗粒的分级作业。在新型水力旋流器的研发过程中，将新型水力旋流器应用于实际工况，并实时监测旋流器的工作参数，虽然有数据准确、能够综合考虑现场复杂因素等优点，但难以观测水力旋流器内部流体运动情况，难以获得水力旋流器压力场、速度场，并且耗费资源。流体动力学模拟软件能够预先模拟所设计的水力旋流器在某工况下的运行参数，并且能够直观地显示参数异常点的位置。

通过 CFD 仿真模拟，有学者针对优化水力旋流器的结构以及提高分级效率，进行了优化研究工作，并取得了一定的进展。魏可峰等人[1]通过 Fluent 软件探究了φ50 mm 旋流器锥角变化对旋流器内部流场及分级效率的影响，采用雷诺模型计算湍流，以 VOF 模型模拟气-液两相流场，最后采用 Mixture 模型考察了锥角对分级效果的影响。陈志强等人[2]通过 Fluent 软件探究了旋流器结构的改变对水力旋流器内部流场的影响，分析了旋流场内部循环流和盖下流的分布特征，为水力旋流器的结构优化提供了一定依据。王学涛等人[3]通过 Fluent 软件探究了不同给矿压力下，20 µm 以下颗粒在φ50 mm 旋流器中的分级效果，模拟数值接近试验数值。M.P.Schearz 等人[4]通过 CFD 模拟数值预测水力旋流器的性能，当流体中固体体积分数较高时，预测值可能有不确定性，但对于水力旋流器性能预测仍然有一定的参考价值。H.Razmi 等人[5]通过 CFD 模拟了操作参数 (颗粒密度、固体颗粒入口质量流量、入口进料速度等) 以及设计参数 (旋流器直径、高度、筒体长度、锥形段长度、入口类型等) 对水力旋流器性能的影响，通过优化结构提高了水力旋流器的分级效率。

本研究的主要目的是通过 CFD 模拟获得某型号旋流器不同流量下的压力分布，从而获得流量随压力的变化曲线，为旋流器选型提供参考依据，并将数值模拟结果与试验数值对比，以验证数值模拟结果的可靠性。

1 几何模型的构建

采用 UG NX11.0 构建了适用微细颗粒分级的水力旋流器模型。旋流器结构如图 1 所示，图中 Z1、Z2、Z3、Z4为旋流器的 4 个截面；其主要参数如表 1 所列。

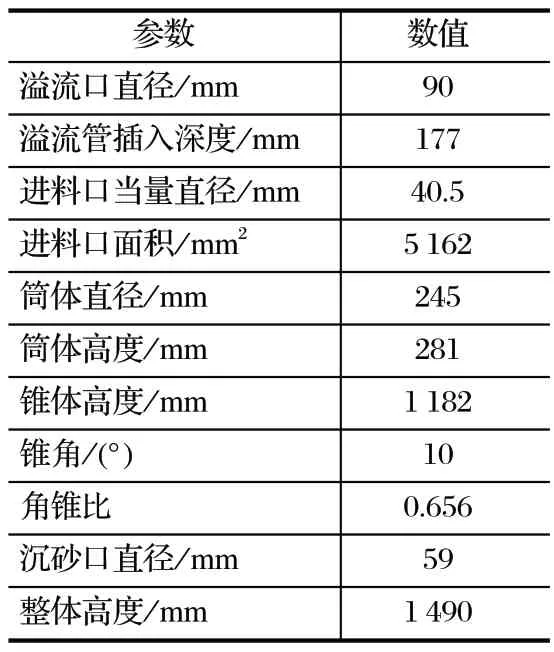
表1 旋流器的主要参数Tab.1 Main parameters of hydrocyclone

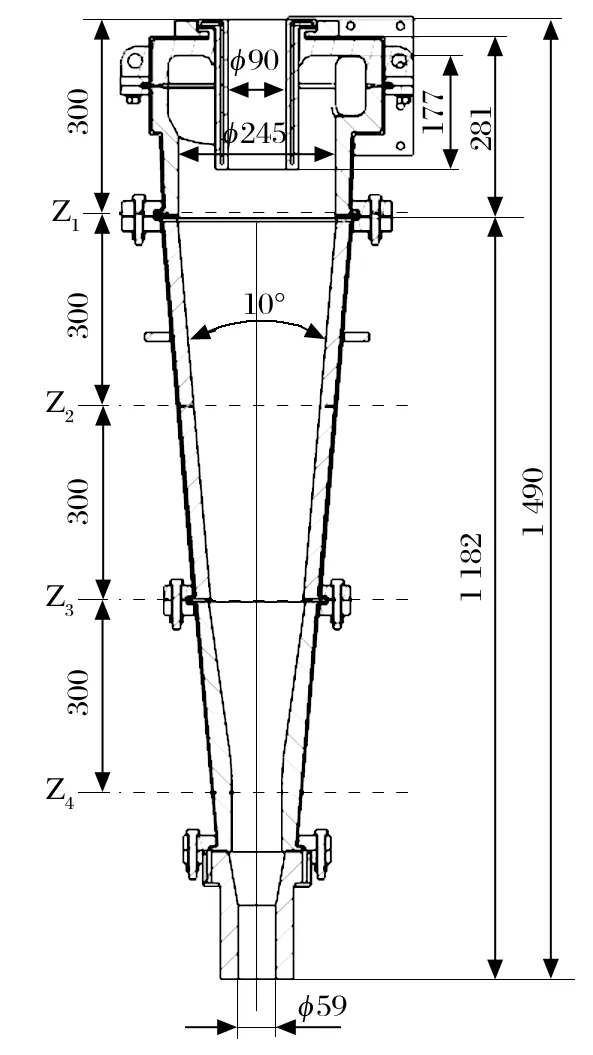
图1 旋流器结构Fig.1 Structure of hydrocyclone

2 数学物理模型及经验公式

2.1 雷诺应力模型控制方程

水力旋流器内部流体运动形式是一种由半自由涡流和强制涡流耦合而成的复杂螺旋涡流，通常采用雷诺应力模型 (RSM) 解决这种带有强烈旋转流动的问题。雷诺应力模型控制方程为

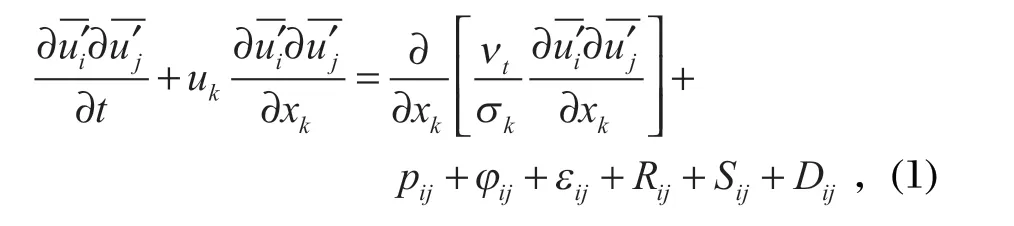
式中：ui为速度在i方向上的分量，m/s；uj为速度在j方向上的分量，m/s；t为时间，s；xk为笛卡尔坐标分量；νt为湍流黏度，m2/s；σk为k方程的普兰特数；pij为应力项；φij为源汇项；εij为黏性耗散项；Rij为旋转项；Sij、Dij为方程柱坐标表达式的曲线项。

2.2 分级效率计算公式

分级效率计算公式包括分级量效率公式和分级质效率公式，当原料中细粒级含量不高时，用量效率公式计算；当原料中细粒级含量很高时，则用质效率公式计算。在实际生产中，大多数情况下都采用质效率公式计算。

式中：α为给矿中的某一粒级含量，%；β为溢流中的某一粒级含量，%；θ为沉砂中的某一粒级含量，%。

2.3 处理量经验公式

根据生产实践和科学试验测定资料，有学者运用数学统计分析，得到了水力旋流器处理量qm的经验计算公式[5]，有达尔斯特罗姆 (D.A.Dahlstrom) 算式、庞学诗算式和波瓦罗夫经验算式。

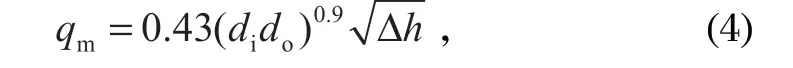
达尔斯特罗姆算式为式中：di、do分别为给矿口、溢流口直径，cm；Δh为给矿水头，mH2O。

庞学诗通过最大切线速度轨迹法计算，得到了水力旋流器最大处理量的一般公式：

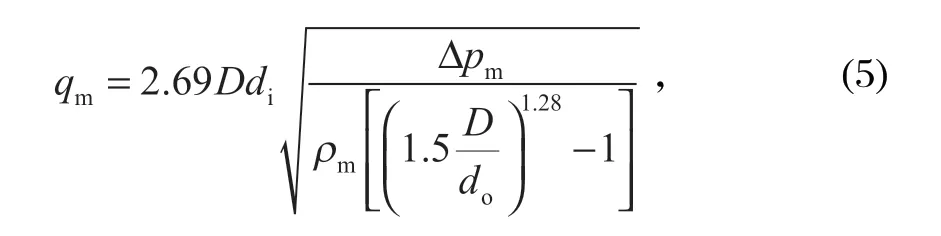
式中：D为旋流器的生产能力，m3/h；Δpm为给矿压力 (最大实际压降)，MPa；ρm为给矿矿浆密度，kg/m3。

波瓦罗夫根据空气柱界面法，导出了旋流器生产能力的经验公式。在我国以往的选矿设计中，旋流器的选型计算基本采用该方法，其公式为

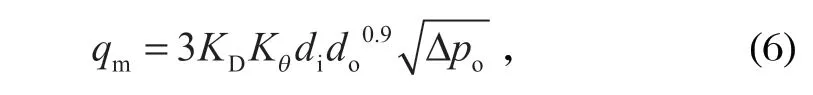
式中：KD为旋流器直径修正系数 (250 mm 旋流器该值为 1.14)；Kθ为旋流器锥角修正系数；Δpo为旋流器工作压力，MPa。

当旋流器直径大于 500 mm 时，需要考虑旋流器本身高度的压力：

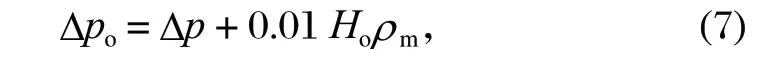
式中：Δp为旋流器入口压力，MPa；Ho为旋流器高度，m。

3 数值模拟

3.1 网格划分及网格无关性检测

采用四面体划分法 (Tetrahedrons) 划分网络，且采用 Patch Conforming，充分考虑几何体的微小特征，采用 Inflation 设置边界层，Inflation Option 采用 Smooth Transition 选项，边界层层数设置为 5 层，Growth Rate 设置为 1.2。

考虑到仿真结果的准确性，需要对网格进行无关性检测[6]，网格数量选取 255 503、413 594、560 417、632 301、695 235、756 513 个，变量选取 80 m3/h 下的进口压力，检测结果如图 2 所示。由图 2 可知：当网格数量增加时，进口压力不断增大；当网格数量为 695 235 个时，旋流器进料口压力趋于稳定，绝对值误差小于 3%，满足网格无关性要求。最终确定旋流器流体区域划分网格数量为 695 235 个，可同时满足计算精度和计算速度的要求。

图2 网格无关性检测Fig.2 Network irrelevance detection

3.2 数值条件与边界条件

流体设置：流体为固液混合的矿浆，密度为 1 340 kg/m3，黏度为 0.001 452 Pa·s。环境条件设置：重力加速度为 9.8 m/s2，壁面按照标准无滑移界面处理。连续相边界条件设置速度进口 velocity-inlet，40、60、80、100 m3/h 流量下的进口速度分别为 2.15、3.23、4.30、5.38 m/s；溢流口和沉砂口设置为压力出口 pressure-outlet，出口压力均设为 0，以进口和出口的流量差小于 0.1% 为收敛依据。

在流场基础上，进行 DEM 离散相数值模拟，在进口面加入粒径小于 0.045 mm、密度为 2 600 kg/m3的固体颗粒；DEM 体积分数为 11.76%，质量分数为 34.21%；颗粒射流形式采用面射流源，入射初始速度与进口连续相速度相同；颗粒假定为球形，不考虑颗粒间相互作用，由于颗粒质量分数低，且颗粒密度低，与连续相密度相差大，颗粒所受到的虚拟质量力和压力梯度力等作用力可忽略。离散相溢流口设置为逃逸 (escape)，底流口设置为捕捉 (trap)，壁面设置为反弹 (reflect)[7]。

3.3 数值求解方法

由于旋流器内部流体以复杂强旋流的形式运动，故采用适应强旋流的 Reynolds Stress (7 eqn) 模型和 SIMPLE 求解方法。通过经验公式和 Fluent 数值模拟分别得到旋流器的处理量，并将两数据与试验数值对比，以验证 Fluent 数值模拟的可靠性。再结合 DEM 离散相模型，分析旋流器的分级效率，与试验数据对比，以验证其准确性。

4 结果与分析

4.1 旋流器压力云图分析

在流量为 80 m3/h 的条件下，旋流器的压力分布如图3 所示。在 4 个旋流器截面 Z1、Z2、Z3、Z4处分析旋流器在不同流量下，其压力随径向坐标的变化，结果如图 4 所示。

图3 旋流器压力分布云图 (Q=80 m3/h)Fig.3 Pressure distribution contours of hydrocyclone (Q =80 m3/h)

图4 4 个横截面处的压力分布曲线Fig.4 Pressure distribution curve at four cross-sections

由图 3、4 可知，不同流量下，旋流器运行稳定，随着流量的增加，空气柱几乎没有波动，尤其是靠近沉砂口处扰动较小，有利于提高分选效率[8-9]。旋流器的压强由壁面向空气柱不断递减，靠近壁面处压强最大，与实际情况相符合，压强分布连续性较好，流体由进口进入旋流器速度梯度小，无较大扰动。分别在 Z1、Z2、Z3、Z4截面处作压力随径向坐标变化曲线，由旋流器内壁向内，随着半径的减小，压力不断减小，在径向坐标±0.045 m 范围内，压力为负值，对应旋流器流体中的内旋流与实际情况相符合。

4.2 速度场数值模拟分析

旋流器内的速度场包括切向速度、径向速度和轴向速度，速度场能够体现结构变化所导致的流场变化，对循环流、盖下流和短路流的分布提供了依据[10]。旋流器切向速度等值线如图 5 所示。

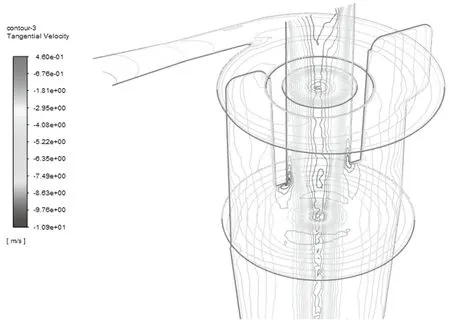
图5 旋流器切向速度等值线Fig.5 Isopleth of tangential speed of hydrocyclone

由图 5 可以看出：由于单入口的原因，进口处等值线呈不均匀偏心状；旋流器进口横截面变化幅度较小，采用渐开线壁面，进口速度梯度较平缓；旋流器室内流体较稳定，切向速度等值线连续均匀，并且扰动较小。

以距离溢流口 300 mm 位置的横截面 (Z1) 为例，旋流器在不同流量下的速度分布如图 6 所示。从图 6 可以看出，不同流量下的切向速度分布呈经典的兰金涡结构，切向速度分布曲线对称性较好。溢流管中心处切向速度最低，溢流管下方流体切向速度最大，这是由于较大的负压使得液体速度增加所导致[3]，随着半径增大，切向速度不断减小。随着流量的增大，靠近外壁处的流体切向速度不断增加，但增加幅度逐渐变缓。随着流量的继续增大，溢流管外侧切向速度变化幅度较大，溢流管内侧切向速度变化幅度较小，靠近中轴线处的切向速度在各流量下几乎保持一致。

图6 不同流量下 Z1 横截面处的切向速度分布曲线Fig.6 Distribution curve of tangential speed at cross-sections Z1 at various flow

旋流器轴向速度等值线如图 7 所示。由图 7 可知，旋流器锥体和沉砂口速度的等值线连续性较好，靠近沉砂口处扰动较小。

图7 旋流器轴向速度等值线Fig.7 Isopleth of axial speed of hydrocyclone

以 Z1横截面为例，旋流器在不同流量下的轴向速度分布如图 8 所示。从图 8 可以看出：不同流量下的轴向速度分布对称性较好，靠近壁面处为下旋流，靠近空气柱部分流体为上旋流。不同流量下，±0.05 m 位置处轴向速度值几乎保持一致；随着流量增大，中心轴线位置处的轴向速度变化幅度较小，旋流器内壁及溢流管两侧区域轴向速度不断增加；随着流量继续增大，零速包络线向中心轴线靠拢。

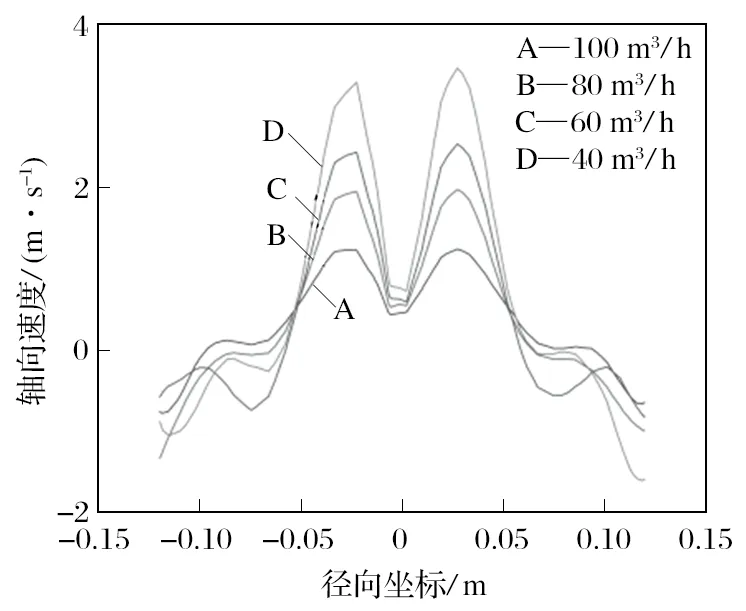
图8 不同流量下 Z1 横截面处轴向速度分布曲线Fig.8 Distribution curve of axial speed at cross-section Z1 at various flow

旋流器数值模拟径向速度分布规律不明显，这可能与单相流场的特性及运动规律有关。

5 试验验证

5.1 试验参数与经验公式对比分析

试验测试了在 96.7～ 149.7 kPa 范围内旋流器处理量的变化，试验结果表明：实际测试结果与数值模拟所得到的结果差异较小；相同入口压力下，模拟数值略偏高，模拟数值与实际数值差值在 2%～ 5%，最大处理量偏差在 4.25 m3/h 以内；随着进口压力的增大，两者偏差呈减小趋势。

对比分析了由几种经验公式计算所得的旋流器处理量数值，结果如图 9 所示。

图9 预测处理量随进口压力变化曲线Fig.9 Variation curve of inlet pressure with predicted throughput

由图 9 可知，庞学诗公式和达尔斯罗姆的计算结果相似，而波瓦罗夫公式计算误差较大。其中，庞学诗公式偏差最小，偏差在 3%～ 6%，最大处理量偏差为 4.95 m3/h，随着进口压力的增大，偏差呈增加趋势；达尔斯罗姆公式偏差略大于庞学诗公式，偏差在 5%～ 8%，最大处理量偏差为 6.64 m3/h；波瓦罗夫公式的计算数值与实际试验数值相差较大，无法为旋流器选型提供参考。综上所述，不同经验公式之间的计算结果存在一定偏差，且各经验公式有一定的适用范围，Fluent 数值模拟所得结果精度最高。

5.2 分级效率结果验证

通过离散相模型 (DEM) 进行数值模拟，获得旋流器模型对 0.045 mm 颗粒的分级效率，通过与试验数值对比，以验证 DEM 模拟的准确性。由于模拟分析中只涉及 0.045 mm 颗粒的分级，所以采用以下公式计算分级效率，该数值与分级量效率公式计算数值相同。

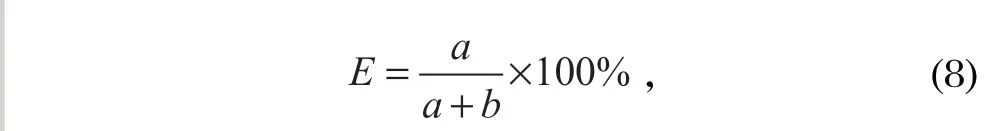
式中：a为模拟分级中由溢流口排出的某粒径颗粒含量，%；b为模拟分级中由沉砂口排出的某粒径颗粒含量，%。

现场实测的旋流器分级数据如表 2 所列。旋流器在不同处理量下的实测分级效率和 DEM 仿真数值的对比如图 10 所示。

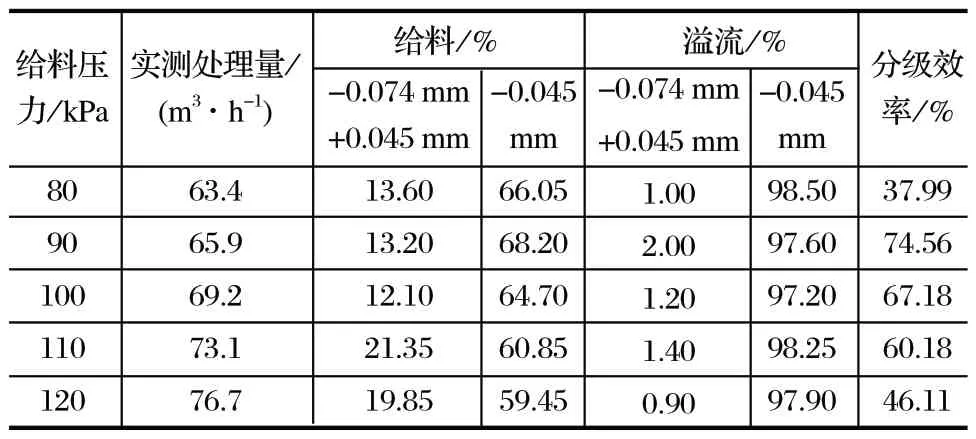
表2 旋流器实测工作数据Tab.2 Measured working parameters of hydrocyclone

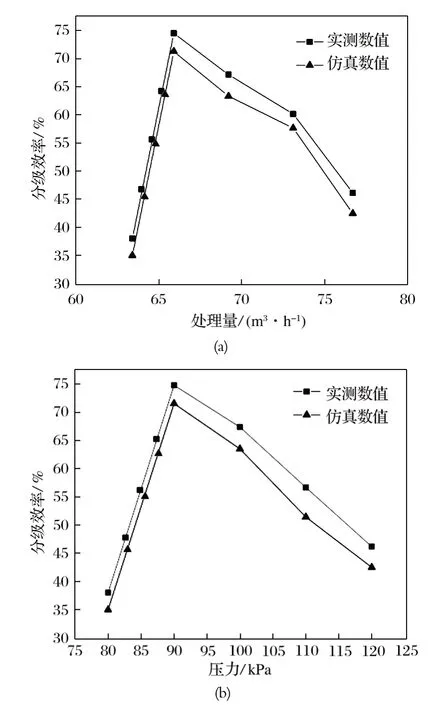
图10 分级效率随压力及处理量变化曲线Fig.10 Variation curve of classification efficiency with pressure and throughput

由图 10 可知：仿真数值接近实测数值；在处理量为 65.9 m3/h 时，实测分级效率和仿真分级效率均达到最大，最大值为 74.56%。但是实际应用中，旋流器分级效率达到 60% 左右即达到分选要求，考虑到现场成本和处理量等问题，现场采用 70～ 75 m3/h 处理量较为合适 (进口压力为 100～ 110 kPa)。

6 结论

通过 Fluent 数值模拟方法，探究了某旋流器内部流体速度分布、压强分布以及空气柱的状态，结果表明：旋流器空气柱在各流量下有较好的稳定性，压强分布均匀，进口向旋流室过渡处压强梯度较小，速度分布符合实际情况，速度等值线分布均匀。

(1) 通过试验测试了旋流器在不同进口压力下的处理量，并利用经验公式 Fluent 数值模拟了旋流器在各进口压力下的理论处理量。Fluent 数值模拟最准确，偏差在 2%～ 5%。经验公式计算偏差大于 Fluent 数值模拟偏差，并且不同经验公式之间计算数值可能有较大偏差，难以根据实际情况作出调整。

(2) 对比了不同处理量下，Fluent 数值模拟所获得的分选效率和试验分级效率，验证了数值模拟结果的准确性。