一种六轴机器人的三维可视化仿真程序设计

蔡嘉晖，王红伟，王漪梦

(1. 北方工业大学机械与材料工程学院，北京 100041；2. 北京航天测控技术有限公司，北京 100041)

1 引言

近年来，我国工业机器人产业呈现“快速成长”和“国产替代”双重特征，对于机器人的研究越来越受到重视，国家提出了工业2025计划，确定了工业机器人的发展和应用是我国制造业走向高端化和智能化的重中之重。在机器人研究过程中，机器人仿真技术可以帮助研究人员了解机器人的运动特性，设计合理的运动控制算法并进行分析验证，提前解决机器人在设计制造和运行方面的问题，能大幅降低研究成本，对机器人的研究提供便利性。

目前，国外有着如robotics机器人工具箱、DMWorks和Robotmaster等成熟的机器人仿真软件，许多研究人员也通过其进行机器人仿真技术的研究，如余乐、穆煜、石磊等通过matlab的robotics机器人工具箱进行机器人的仿真技术研究[1-3]；高艺、吕明珠等借助DMWorks和Robotmaster专用机器人仿真软件进行工业机器人的模拟仿真研究[4，5]。然而上述几种机器人仿真软件都都是封装好的机器人仿真集成库，存在一定的局限性，无法根据自身需求进行功能删减，其应用扩展有较大的限制，对于某些国产或自研机器人无法提供支持。同时，在国内也缺少相关成熟的机器人仿真软件，无法满足国内对于机器人研究的大量需求。

故本文以AUBO-I5型协作机器人为研究对象，提出了一种基于OpenGL图形库和C++编程软件的三维可视化仿真程序设计方法，其结构简单，操作简便，具有良好的扩展性。首先利用Solidworks创建机器人零件模型，建立机器人D-H模型求解机器人的运动学正逆解，根据“行程最短”法来选取机器人运动最优解。最后搭建的机器人三维可视化仿真程序，可对机器人进行运动学仿真，并通过TCP连接真实机器人实现了仿真运动示教实验，验证了所提出机器人运动学算法的正确性。

2 机器人运动学分析

2.1 机器人的正运动学求解

工业机器人由各连杆连接而成，根据D-H坐标系建立准则可以确定相邻两连杆之间的转换关系，通过图1所示的机器人D-H坐标系，可以确定机器人的D-H参数表如下所示。假设第i-1坐标系到第i坐标系转换的四个参数为[6]：θ为关节转角，α为两关节扭转角，d连杆长度，a两连杆间偏置距离，其中只有关节转角θ为变量，其余均为常量。

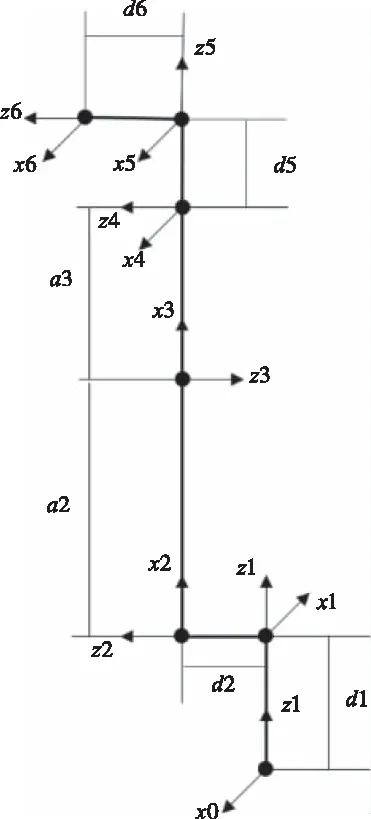
图1 机器人D-H坐标系

表1 AUBO-I5机器人D-H参数

根据机器人D-H参数确定相邻两连杆i-1和i之间的相对关系可知

Trans(0，0，di)·Rot(zi，θi)

(1)

机器人末端的位姿可描述为

(2)

其中：

nx=-s6c1sθ1-3-4-c6(c5c1cθ4-3+2+s1s5)

ox=s6(c5c1cθ4-3+2+s1s5)+c6c1sθ4-3+2

ax=s1c5-s5(c4(c1s2s3+c1c2c3)+s4(c1c2s3-c1s2c3))

px=d6(c5s1-s5c1cθ3-2-4)-a3c1cθ2-3+d2s1-d5c1sθ3-2-4-a2c1s2

ny=c6(c1s5-c5s1cθ3-2-4)-a3c1cθ2-3+d2s1-d5c1sθ3-2-4-a2c1s2

oy=-s6(c1s5-c5s1cθ3-2-4)-c6s1sθ3-2-4

ay=-c1c5-s5(c4(s1s2s3+s1c2c3)+s4(s1c2s3-s1c2c3))

Py=-a3s1cθ3-2-d2c1-d6(c1c5+s5s1cθ3-2-4)-d5s1sθ3-2-4-a2s1sθ3-2

nz=s5c6cθ3-2-4-s6cθ3-2-4

oz=-c6cθ3-2-4-c5s6sθ3-2-4

az=s5sθ3-2-4

Pz=d1-d5cθ3-2-4+a3sθ3-2+a2c2+d6s5sθ3-2-4

其中s1=sin(θ1)、θ1-3-4=θ1-θ3-θ4，其它相同。

2.2 机器人的逆运动学求解

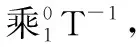
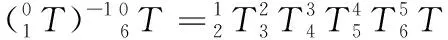
(3)

根据方程左右两边矩阵对应元素相等原则，即L(2，3)=R(2，3)、L(2，4)=R(2，4)可得

θ1=atan2(-py+d6ay，-px+d6ax)-atan2(d2，±A)

由等号两边矩阵对应元素相等可得

θ5=atan 2(±B，axsθ1-nycθ1)

同理可得

(4)

同理

θ4=atan2(Hc(θ2-θ3)-Is(θ2-θ3)，Ic(θ2-θ3)+Hs(θ2-θ3))

其中

C=d5E+d6(axcθ1+aysθ1)-pxcθ1-pysθ1

D=pz-d1-azd6-d5(nxcθ6+nzsθ6)

E=cθ6(oxcθ1+oysθ1)+sθ6(nxcθ1+nysθ1)

H=-cθ6(oxcθ1+oysθ1)-sθ6(nxcθ1+nysθ1)

I=ozcθ6+nzsθ6

机器人θ1、θ5、θ3有两个解，其余为一个解，因此得到在机器人非奇异位置，末端位姿对应8组理论解。

2.3 机器人最优解的选取

通过逆运动学求解得到的机器人关节角度有8组解，但在实际的机器人控制中只需要选取一组最适合的解作为最终的可行解。最优解的筛选原则有“行程最短”准则，能量消耗最小准则、运动最平稳准则等，根据AUBO-i5机器人的结构特点和控制原理，本文将基于“行程最短”准则选取机器人的最优可行解[8]，同时遵循大臂少动，小臂多动的原则，引入大臂加权系数ω1，小臂加权系数ω2。最短行程准则最优解的选取流程如图2所示。

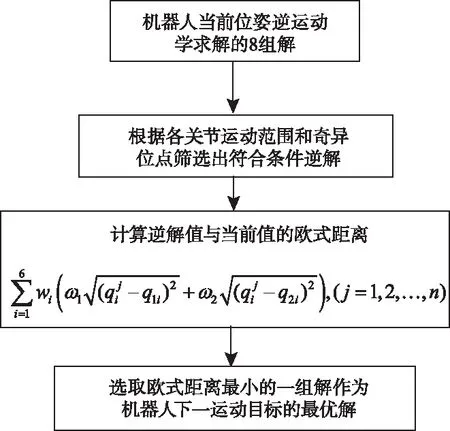
图2 最短行程准则算法流程图

3 三维可视化方程程序的设计

机器人的三维可视化仿真程序通过C++编程软件进行搭建，包含机器人的三维模型和数据通讯两部分，它能模仿机器人的真实三维模型同时具有真实机器人的运动学关系，可在人机分离环境中有效实现机器人的运动可视化并对机器人进行动作示教控制。

1)创建机器人零件模型

机器人分为底座和机械臂1到机械臂6一共7个零件。在solidworks中根据AUBO机器人的真实结构参数，对机器人各零件进行建模，并确定各零件的零件坐标系，各零件模型如图3所示。

图3 机器人各零件模型

把机器人模型文件转换为obj格式的文本文件，其原理是把三维模型表面分解纷若干个三角面，把各三角面的三点坐标进行保存。

3)C++重建机器人模型

根据机器人的结构，确定各零件的初始位置和姿态，确定个零件坐标系在机器人坐标系下的相对位置，通过C++读取obj文件，在确定的坐标位置下绘制零件，构造整体的机器人仿真模型。

4)代入机器人运动学

确定机器人各关节的转角范围，设计关节类型和关节驱动，根据搭建的机器人仿真模型，代入上述的机器人正逆运动学方程，使机器人仿真模型具有运动学关系。

5)数据通讯

机器人的三维可视化仿真程序可与真实机器人进行连接，可实时反馈机器人的运动信息并对机器人进行运动控制。机器人与仿真软件的控制流程如图4所示，仿真软件通过按键和示教输入得到机器人位姿增量，计算出机器人运动目标位姿，然后根据逆运动学算法计算出机器人的各组逆解，结合机器人当前关节角度得到机器人的运动目标最优解，最后更新系统数据，从而控制AUBO机器人的运动以及更新软件的三维仿真图像显示。

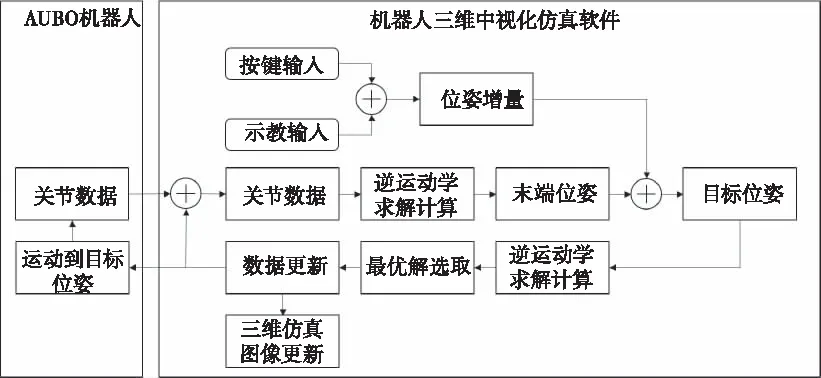
图4 控制流程

机器人的三维仿真软件界面如图5所示，可实时显示机器人的关节角度和末端位姿信息，同时可通过点击程序按键和编程两种方式对连接的真实机器人进行动作示教控制。

图5 三维可视化仿真软件界面

4 三维可视化程序的运动学仿真

4.1 正运动学算法验证

由于三维可视化仿真程序与D-H法构建的运动学模型的零位不同，因此需要在机器人仿真程序中代入初始关节角度θ，使两者零位统一。在AUBO机器人示教器上选取5组关节角度作为机器人正解算法的输入，通过计算可得机器人在对应关节角度下末端坐标系在基坐标中的位置矢量，其结果如表2所示。

“周长”与“面积”是从不同维度对空间的度量。周长限于一维空间，面积发展至二维空间。小学生对面积理解的基本趋势是：从面积表征与长度表征或周长表征混淆，到最后分化为清楚的面积表征。因此，让学生建立面积概念的初始阶段，应注重多种对比的方式，帮助学生区别。前期对于两者的区分主要停留在“描周长、涂面积”的阶段，实践下来学生对两者的区分还是不够明晰，后期还可从以下方面继续落实。

表2 正运动学算法验证数据

对比AUBO机器人与正解算法结果，可知两者在相同关节角度下对应的工具坐标系位置矢量完全一致，同时仿真程序与真实机器人的姿态相同，从而验证了所提出运动学正解算法的正确性。

4.2 逆运动学算法验证

随机选取一组机器人的关节角度(40°，20°，-30°，70°，120°，-50°)，通过正运动算法得到机器人的末端位姿为(-378.836，-415.134，742.833，68.829，-40.776，-7.946)，把改组位姿输入机器人逆运动学算法中，可以得到机器人对应关节的8组解，其数值如表3所示。

表3 逆运动学验证数据

图6为机器人运动学逆解对应关节角度的三维仿真位形结果显示，可以看到8组逆解对应的机器人末端位姿是一致的，且等于选取的初始角正解计算结果，从而证明了正逆运动学算法的可逆性和正确性。通过比较运动学逆解关节角度和三维仿真结果图，考虑关节运动范围和杆件干涉等因素，可知第8组逆解超过了机器人4轴的关节运动范围，排除不合理的逆解，其余七组逆解均符合运动要求，然后通过“行程最短”法进行处理，进而得到机器人运动的一组最优逆解。

图6 机器人逆解对应位形

5 示教实验验证

本文构建的机器人三维可视化仿真系统可通过TCP连接机器人，得到机器人的关节角度及末端位姿，对机器人进行实时的三维显示，同时能通过仿真程序对机器人进行示教控制，分为按键和编程两种示教方式。图7为本次机器人仿真示教控制的实验平台。

图7 仿真软件实验平台

如图8所示，图8(a)是通过虚拟按键对机器人进行关节控制和末端位姿控制，图8(b)是通过输入代码进行编程示教。在仿真软件的机器人控制实验中，其仿真三维模型与真实机器人位形相同，同时其关节角度和末端位姿参数相同，证明仿真软件的机器人运动学算法与AUBO机器人一致，通过仿真软件对机器人的动作示教控制是可行的。

图8 仿真软件机器人控制实验

6 结论

本文以AUBO-I5型机器人为研究对象，基于C++和OpenGL提出了一种机器人的三位可视化仿真程序设计方法，通过Solidworks建立了机器人的各零件模型，分析了机器人的正、逆运动学求解方法和最优解的选取问题，并对比真实机器人验证了算法的正确性。同时，仿真程序能连接真实机器人，能对其进行控制示教，对于机器人的控制研究提供了一定的便利性。本文设计的机器人三维可视化仿真程序具有模型逼真，动画刷新率高等优点，同时基于C++的编程软件扩展性强，能针对各种控制条件和末端执行器进行功能扩展，对于后续机器人的设计与控制研究奠定了基础。