基于多目标优化的智能网联汽车队列换道方法
闫茂德,张钰瑶,杨盼盼,谢 欢
(长安大学电子与控制工程学院,陕西 西安 710064)
1 引言
智能网联汽车作为未来智能交通系统的重要发展方向,在缓解交通拥堵、减少能源消耗、提升交通安全等方面具有显著优势[1][2],以纵向编队为代表的智能网联汽车队列控制是当前的研究热点。随着研究的不断深入,简单的纵向车队行驶已不能满足实际交通需求,复杂路况如强制换道场景下的智能网联汽车队列控制得到了许多学者的关注。当车辆队列前方出现障碍物或前方为匝道/合流区,都需要车队在有限换道距离内完成换道行为,即强制换道工况。如何综合考虑交通、道路、车辆因素,在强制换道这一场景下完成汽车队列的换道控制是值得研究的重要问题。
目前,国内外学者从不同角度对强制换道问题展开了研究。文献[3]针对高速公路入口匝道区车辆合流问题,提出了一种让换道车辆依次进入目标车道不同车辆间隙中的算法。文献[4]针对多个车道合流的场景,运用回归树的方法将换道合流问题转化为合流区车辆重新排序的问题。文献[5]根据前方障碍物路况,为智能汽车规划了两段式紧急换道轨迹,提高了车辆换道对复杂道路工况的适应性。以上研究多针对单个车辆的换道行为,但智能网联汽车通常以队列形式行驶,需要进行强制换道的对象为整个车队。针对队列换道问题,文献[6]通过对头车进行规划,对跟随车建立基于方向与速度的综合决策模型,在交叉路口前完成了队列换道。但换道轨迹基于多段线简单拼接而成,缺乏对道路通行效率、驾乘舒适性以及燃油经济性等指标的考量,并非当前道路环境下的最优轨迹。文献[7]以换道过程中的乘客舒适度与换道距离为目标,规划了两车换道最优轨迹,但仅研究了自由换道场景,也未对队列行驶的能耗问题进行讨论。
综上所述,本文针对智能网联汽车队列强制换道场景,提出一种考虑换道过程中多种优化目标的智能网联汽车队列强制换道方法。将队列强制换道问题分解为换道最优轨迹规划问题及队列轨迹跟踪控制问题。最优轨迹规划过程中综合考虑换道距离、行车安全及车辆动力学等约束条件,同时达到提升道路通行效率、驾乘舒适性以及燃油经济性等优化目标。队列中的跟随车采用滑模控制器跟踪期望的换道轨迹,换道过程中前后车保持安全间距。最后,通过Matlab对本文所提出的多目标优化的汽车队列强制换道方法进行了仿真验证。
2 问题描述
由一辆领航车(标记为V0)、N辆跟随车(标记为V1-VN)组成的智能网联汽车队列行驶在同一车道上,初始时刻相邻车辆之间间距不等。车辆通过传感器获得自身运动状态(位置、速度、加速度和偏向角等),同时通过通信网络实时获得前车的运动状态。
如图1所示,用车辆质心在坐标系的位置与偏向角来表示车辆实际的位姿。对于跟随车Vi,用pi=(xi,yi,θi)T与pi-1=(xi-1,yi-1,θi-1)T分别表示当前车与前向车辆在此刻的纵向位置、横向位置与偏向角。d为车辆编队行驶过程中需要保持的安全间距。
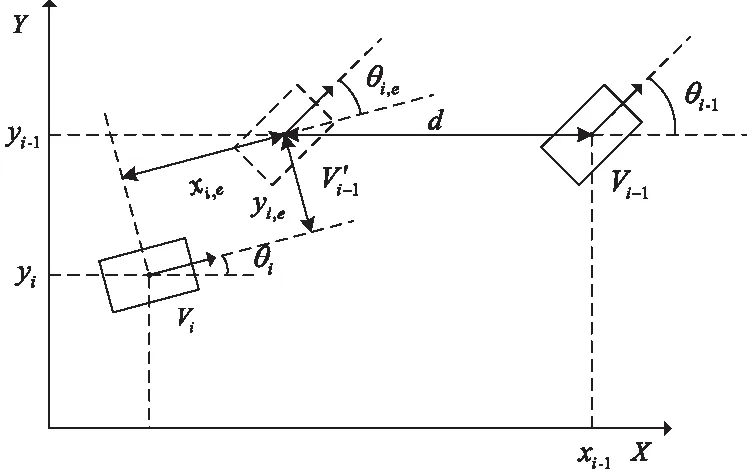
图1 队列中的前后车位姿
vi和ωi表示当前车实际的前向速度和偏向角速度,作为控制输入,二者与车辆实际的位姿有如下关系

(1)
本文综合考虑智能网联汽车队列换道过程中的道路通行效率、驾乘舒适性以及燃油经济性等问题,研究在多优化目标及多约束条件下的车辆队列强制换道轨迹规划与控制方法。换道过程中,跟随车Vi的跟踪目标为V′i-1车,即前向车辆的纵向位置后移d距离后的虚拟目标V′i-1。整个队列进行同步换道,换道过程中车与车之间保持固定安全间距。
3 车辆队列换道轨迹规划与控制
通过考虑强制换道过程中的多优化目标及多约束条件,本节将轨迹规划问题转化为解最优轨迹问题,并设计控制器使跟随车跟踪目标轨迹。
3.1 换道轨迹规划
由于五阶多项式具有三阶连续可导、曲率连续不突变、可纵横向解耦换道轨迹等优点,在此选择五阶多项式作为换道轨迹函数

(2)
式中,x、y分别代表换道过程中车辆纵向与横向的位置,a5~a0、b5~b0为换道轨迹函数中的未知系数。
为求解这12个未知系数,考虑换道车辆初始时刻与终止时刻的边界条件
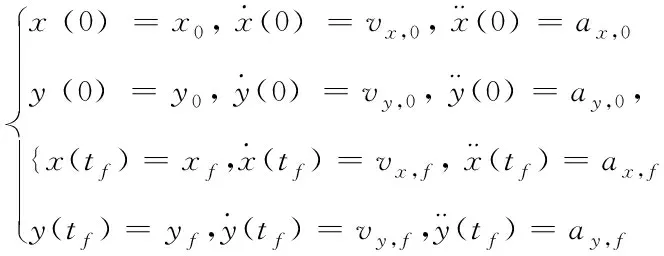
(3)
式中,0代表换道初始时刻,tf代表终止时刻。
以换道初始时刻的车辆质心作为坐标原点,车辆前向方向为x轴,横向方向为y轴建立坐标系,有x0=0,y0=0。假设换道前车辆匀速行驶在原车道上,则vx,0=v0,vy,0=0,ax,0=0,ay,0=0,v0由车辆当下行驶速度给定。车辆向相邻车道换道结束后平稳运行,xf代表换道终止时纵向距离,yf为横向距离,vx,f代表目标车道的平均速度vd,vy,f=0,ax,f=0,ay,f=0。
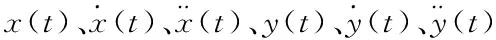

(4)
为了求解强制换道场景下的换道轨迹函数,本文将换道轨迹规划问题转化为多优化目标及多约束条件下的最优轨迹求取问题。目标函数集换道过程中的通行效率、驾乘舒适性以及燃油经济性指标于一体,在多种约束下求取使目标函数达到最优的tf、xf值,从而获得最优换道轨迹。
通过纵向换道距离长短评估换道行为对局部交通流产生的影响,换道距离越短,代表两个车道被占用的路段越短,局部交通的通行效率越高。即
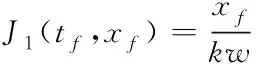
(5)
式中,k为常数,w为车道宽度。
跃度(即加速度的导数)是影响乘坐舒适性的最重要因素之一。跃度越小,越能优化乘客体验。因此有

(6)
式中,jx(t)、jy(t)为车辆的纵向、横向跃度,jx,max、jy,max代表换道过程中允许的最大纵向、横向跃度。
如果忽略发动机工作区域的极端情况,燃油消耗主要由车辆加速水平决定。在相同里程和平均行驶速度的跟驰过程中,车辆的油耗随着其加速度绝对值的增大而增大[8],有
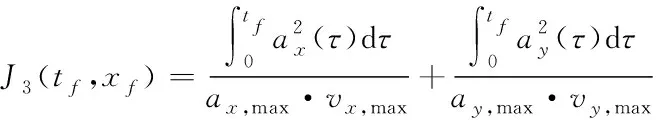
(7)
式中,ax,max、vx,max代表换道过程中车辆动力系统允许的最大纵向加速度、速度,ay,max、vy,max代表换道过程中允许的最大横向加速度、速度。
综上,车辆队列换道时的最优轨迹规划目标函数为
minJ(tf,xf)=k1J1+k2J2+k3J3
(8)
式中,k1、k2、k3为不同指标的权重系数。
为保证车辆队列换道性能,换道过程中需要考虑的约束如下:
1)换道距离受限:当道路前方有障碍物阻碍前行或需换道驶入匝道/合流区时,车辆都需要在特定距离内完成换道行为。此时,换道终止时刻纵向换道距离受到最大允许换道距离xf,max的限制
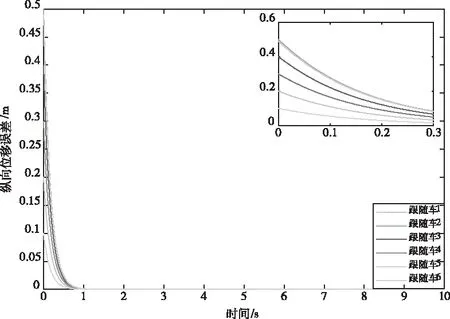
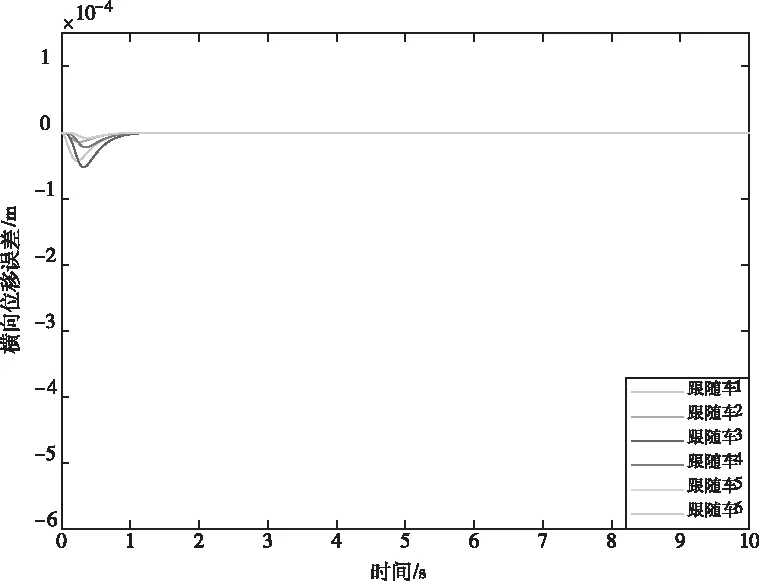
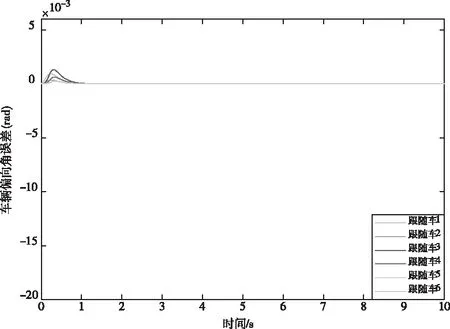
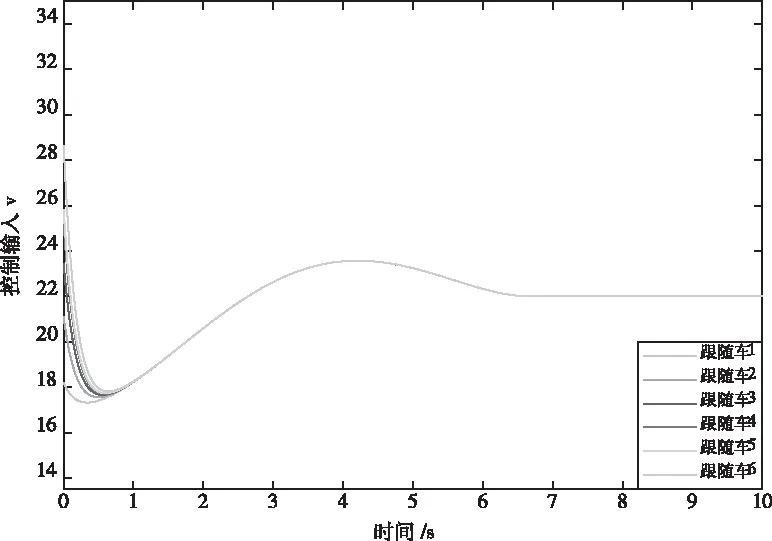
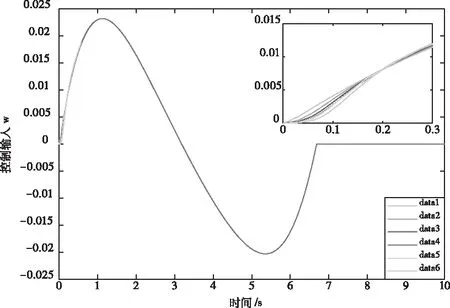
0 (9) 2)行车安全限制:车辆换道时受到道路交通安全法规的限制,横向换道距离不得大于一个车道宽度,与相邻车辆初始间距大于安全距离,即 (10) 3)动力学约束:车辆在行驶过程中因动力系统等因素会受到约束,具体表现为 (11) 至此,轨迹规划过程中以式(2)-(3)形成的12个等式,14个未知数的静不等方程组求解问题被转化为以式(8)为目标函数,以式(9)-(11)为约束条件的最优轨迹求取问题。通过求解最优问题,得到约束条件下使目标函数达到最小的终止换道时间tf、终止时换道距离xf,代入式(4)后得到理想的换道曲线函数。 在以当前车为参考的局部坐标系下,跟踪目标V′i-1车与当前车之间的位姿误差为 (12) 对式(12)进行求导,可得位姿误差的微分方程 (13) 可以证明[9],只要xe收敛到0且θe收敛到-arctan(vi-1ye),则ye会收敛到0。 设计滑模控制器的切换函数 (14) 对于滑模变结构系统,不连续的开关特性会引起系统抖振。为了削弱抖振,加快系统接近切换面速度[10],采用新型趋近律 (15) 其中 式中,0<δ<1,η>0,δ>0,δ为fal(s,η,δ)在原点附近正负对称线性段的区间长度,并且fal(s,η,δ)为非连续函数。当|s|>δ时,式(15)的第二项能加快系统趋近滑动面速度,起到平滑、限幅作用;当|s|≤δ时,式(15)的第一项可以使系统状态在有限时间内快速到达滑模面并有效削弱高频震动现象。 则系统的趋近律可表示为 (16) 将上式整理可得当前车的控制输入vi和ωi为 (17) 为验证本文所提汽车队列强制换道方法的可行性和有效性,考虑由1辆领航车和6辆跟随车组成的车辆队列,在Matlab上进行仿真验证。 选取车辆从低速车道向高速车道换道的场景进行仿真。假设原车道平均车速v0=17m/s,目标车道平均车速vd=22m/s,按照国家标准取两车道间距为3.75m。最优轨迹求取过程中的相关参数见表1。 表1 最优轨迹规划相关参数 将表1中相关参数代入式(8)-(11)中,可求解出终止换道时间tf=6.68s,最短换道距离xf=143.02m,最优换道轨迹曲线如图2所示。 图2 最优换道轨迹 换道初始时刻领航车位姿为x0(0)=62m,y0(0)=0m,θ0(0)=0rad,6辆跟随车的纵向位置、横向位置与偏向角分别为:xi(0)=[51.8, 41.3,30.9, 20.6, 10.5, 0]Tm,yi(0)=[0, 0, 0, 0, 0, 0]Tm,θ0(0)=[0, 0, 0, 0, 0, 0]Trad,与领航者之间的纵向期望间距分别为di,0=[10, 20, 30, 40, 50, 60]Tm,即前后车期望间距为10m。滑模控制器中参数设置见表2。 表2 滑模控制器中参数设置 由1辆领航车,6辆跟随车组成的车辆队列轨迹跟踪控制仿真结果如图3所示。 图3 车辆队列换道轨迹图 图3给出了智能网联汽车队列中所有车辆的行驶轨迹图。可以看出,领航车按照规划的最优轨迹行驶,轨迹平滑曲率连续不突变,完成了一个标准车道宽的换道行驶。6辆跟随车能够实现对领航车辆的轨迹跟踪,且换道过程中前后车之间能保持期望的固定间距10m。在领航车前方换道距离不超过200m的限制条件下,整个车队以同步换道形式完成了队列强制换道的目标。 图4 车队纵向位移误差图 图5 车队横向位移误差图 图4为六辆跟随车在队列换道过程中的纵向位移与跟踪目标纵向位置的误差曲线。可以看到在本文所提队列换道方法的作用下,跟随车的纵向位移误差在1s之内已基本实现收敛,在后面的换道过程中也没有发生过突变,充分证明轨迹跟踪控制方法的有效性。图5为六辆跟随车的横向位移与跟踪目标横向位置的误差曲线,在整个换道过程中横向位移误差很小(≤6×10-5m),很好地保证了轨迹跟踪的准确性与稳定性。 图6 车队偏向角误差 图6为车队轨迹跟踪的偏向角误差图,在轨迹跟踪控制器的作用下,6辆跟随车在整个换道过程中车辆偏向角误差均不超过1.3×10-3rad,很好地保证了队列同步换道过程中的位姿准确性。 图7 车队控制输入v 图8 车队控制输入w 图7、8分别为6辆跟随车在换道过程中的控制输入v、控制输入w,代表车辆沿着偏向角的前向速度以及车辆偏向角速度。初始时刻受换道位姿误差影响,控制输入v较大,但28.66m/s的峰值仍小于车辆速度限制值。跟随车从平均车速17m/s的原车道换至平均车速22m/s的目标车道过程中,控制输入v均未超过速度限制值,控制输入w的变化趋势代表车辆偏向角先增大后减小,符合实际交通中车辆换道的偏向角变化规律。在规划的换道终值时间之后跟随车以22m/s的前向速度及0rad/s的偏向角速度,平行于目标车道中心线匀速行驶。 本文针对智能网联车辆队列强制换道问题,提出了基于多目标优化的队列强制换道方法。领航车综合考虑道路通行效率、驾乘舒适性以及燃油经济性等优化目标,并结合换道距离、行车安全及车辆动力学等约束条件规划出当前换道环境下的最优换道轨迹,跟随车基于滑模控制器跟踪目标轨迹,整个车队以同步换道形式完成了强制换道工况下的换道目标。
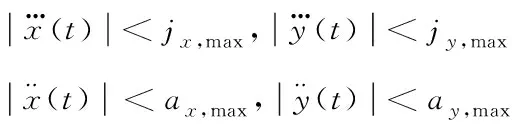
3.2 队列跟踪控制
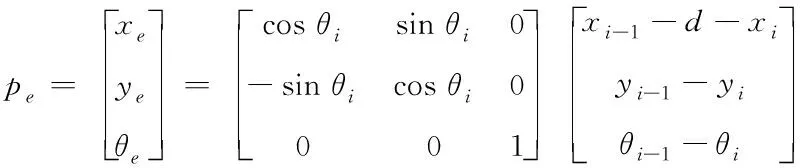

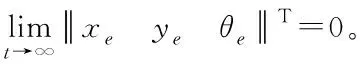
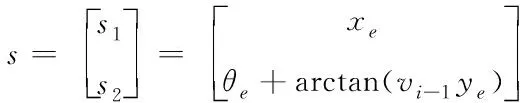
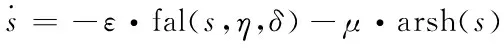
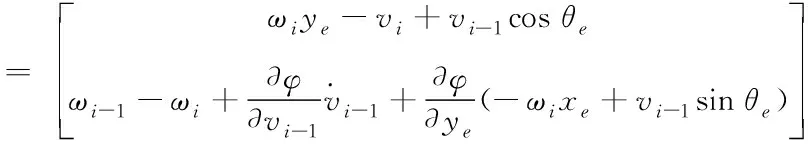
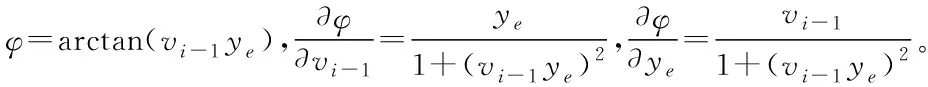
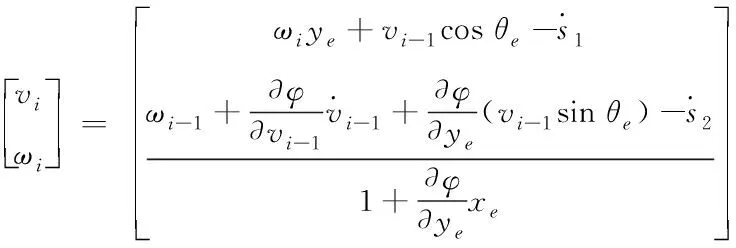
4 仿真结果
4.1 轨迹规划仿真结果

4.2 队列轨迹跟踪
5 结论

