地道桥U型槽结构受力分析及设计研究

鞠炳照　贾晓婵

摘要 沭阳县城区快速路二期工程中，松江路下穿北京南路需采用地道桥。文章以此工程为背景，对地道桥结构的下穿U型槽结构进行研究分析。分析过程中，明确了结构计算时的边界条件、汽车荷载及水平土压力取值方式。研究结果表明，在预设的边界条件及荷载作用下，U型槽结构的强度、裂缝及变形满足设计要求。整个分析过程可为类似的工程设计提供借鉴。

關键词 U型槽结构;边界条件;汽车荷载;水平土压力;强度;裂缝;变形

中图分类号 U448 文献标识码 A 文章编号 2096-8949（2022）06-0102-03

引言

随着社会的发展，城市人口及车辆数量呈现递增式增长，城市拥堵现象愈演愈烈，尤其出现在交通量较大的平面交叉位置。为改善出行条件，城市交通建设中更多的选用立体交叉方式，以提高交叉口的通行能力。下穿式立体交叉（即地道桥）因占地较少，施工工艺简便，被大量应用于道路与道路交叉、道路与铁路交叉。

规划地下快速路交通应具有前瞻性，地下快速路对改善交通拥挤状况、升级城市地下物流系统的发展、改善城市环境具有深远而重要的意义。

1 现实意义

（1）地下快速路建设费用相对较低。地下快速路因为较少的节点设计建造，无须花费较大费用维护复杂的信号控制系统，相比地铁更具有优势。工程建造过程中，将环境进行货币化，即污染造成的损失加入总体造价中，整体造价较为合理。地下快速路建设应当早研究早规划，坚持长期建设，只有达到相当规模才会显现巨大的社会价值及生态价值。

（2）加快建设地下快速路系统，升级城市交通运输方式，将城市货运逐步转移至地下运输，可有效改善交通拥堵状况。根据城市发展规则，货运占城市交通总量比直接与城市的发展水平呈正相关。地下快速路建设可有效推进地下物流系统的发展，增强城市经济发展活力。

（3）地下快速路系统工程与轨道交通及市政工程建设相结合，一体化设计、一体化施工，以节省投资和缩短施工周期。交通建设过程中，土方挖填及运输以及管线临时迁移等，都涉及较大的建设费用。将地下快速路系统同地下轨道交通结合，可大幅度降低成本。

虽然目前多关注于各种结构类型桥梁的建设，但应该看到，地道桥以其更为经济的造价，足可比肩跨线桥梁的使用功能服务于社会。相比于跨线桥梁，地道桥因埋于地下，减少对车辆及行人的视线阻隔，降低了城市空间的拥挤度，因此地道桥应用前景十分广阔。

该文针对地道桥结构中的U型槽结构进行研究。U型槽结构类似于挡土墙结构，但由于底板结构的存在，受力更为复杂。针对土的不同特性，应采用不同的方式模拟土压力以及结构的边界条件。

2 工程概况

沭阳县城区快速路二期工程松江路下穿北京南路设置一座地道桥，全长659 m，敞开段为整体U型槽结构，暗埋段为单箱双室箱体结构，标准横断面净宽为2×14 m。地道桥内采用双向6车道，保证主路车辆快速通过，两侧各设置单向双车道辅路，达到松江路与北京南路地面平交的目的，该文着重研究地道桥U型槽结构。U型槽段按照25 m节段设计，内外面垂直设置，纵断最低点位置，侧墙净高8.0 m，侧墙及底板厚度1.2 m。

3 结构计算

3.1 主要技术参数

3.1.1 设计标准

（1）道路等级：城市快速路。

（2）设计车速：80 km/h。

（3）设计荷载：汽车荷载为城-A级。

（4）设计基准期：100 a。

（5）结构安全等级：一级。

3.1.2 主要设计荷载

（1）自重。按照混凝土容重25 kN/m³进行自重分析。U型槽内铺装结构等采用荷载形式计入。

（2）汽车效应。地道桥内主路采用城-A车道荷载，6车道。

地道桥外辅路引起的土压力按照车辆荷载加载，可按下式换算成等代土厚h（m）计算[1]：

式中：γ——土的重度（kN/m³）;

ΣG——布置在B×l0面积内的车轮总的重力（kN）;

l0——侧墙后填土的破坏棱体长度（m）;

B——侧墙的计算长度。

侧墙的计算长度B（m）按下式计算，但不应超过分段长度（25 m）：

式中：H——侧墙高度。

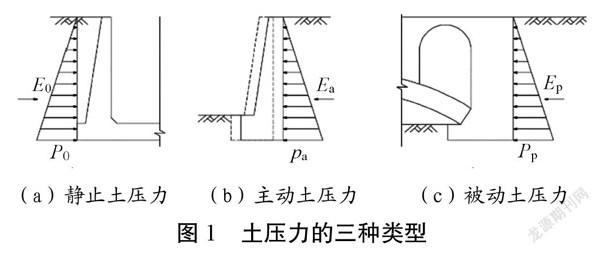
（3）侧向土压力作用。主动土压力、被动土压力可采用库仑或朗肯土压力理论计算。作用于侧墙的土压力和水压力，对砂性土宜按照水土分算计算;对黏性土宜按照水土合算计算。根据地勘信息，工程范围内地质以黏性土为主，故采用水土合算方式。针对静止土压力、主动土压力及被动土压力的选择，可参考图1[2]。

（a）静止土压力 （b）主动土压力 （c）被动土压力

因底板水平支撑作用，侧墙不产生水平位移，U型槽结构可参考图1（a），采用静止土压力。根据地勘报告知，土的内摩擦角α=16°，则有K0=1−sinα=0.724。

（4）温度荷载。初始温度15 ℃，体系按升温25 ℃，体系降温−25 ℃。

3.2 计算模型

地道桥整体计算采用Midas Civil有限元软件，采用板壳单元，侧墙与底板采用固接方式。考虑地道桥结构的侧向土压力作用及铺装，采用面荷载加载。汽车荷载采用车道荷载计算方式。考虑温度作用。

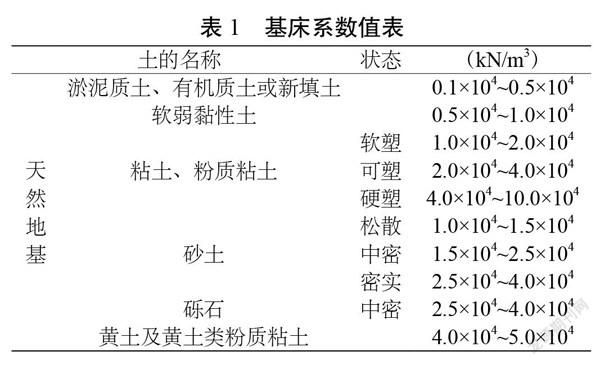
模型边界条件处理：按照弹性地基梁设计，根据文科勒假设：地基上任一点所受的压力强度p与该点的地基沉降量s成正比，p=ks，式中：k称为基床反力系数，简称基床系数。顾晓鲁等主编的《地基与基础》（第三版）[3]，基床系数取值见表1。

实际工程经验分析知，砂土、黏性土的弹性模量远小于混凝土结构的弹性模量[4]。图2以地道桥U型槽结构为例，选取了荷载标准组合作用下，不同基床系数（104～

107 kN/m3）土质对结构内力的影响[5]。分析图表知：

（1）基床系数取值在（104～105 kN/m3）范围内时，结构内力均匀变化。

（2）基床系数取值在（106～107 kN/m3）范围内时，结构内力在L/8处产生突变，且内力值在L/8～L/2范围内变化较小，说明此时土弹簧刚度过大，底板变形受影响较大，此时，不建议采用弹性地基梁法。

综上所述，在仿真模拟过程中，针对黏土、粉土及砂土等，基床系数取值在104～105 kN/m3范围内的，可采用弹性地基梁法，计算精度满足要求。

因侧墙较高，出于节省材料且充分发挥材料作用的目的，结构采用阶梯式，侧墙深度小于或等于3.0 m时，侧墙厚度采用0.5 m，侧墙深度大于3.0 m时，侧墙厚度采用1.2 m。

4 结构分析

结构分析过程中，后期构建验算时，应注意区分侧墙与底板构件的构件属性，以验证两种结构构件的不同受力特性[6]。侧墙构件以受弯为主，可简化为纯受弯构件，承载能力极限状态验算按照《公路钢筋混凝土结构及预应力》（JTG 3362—2018）（以下简称《公预规》）中5.5.2～5.5.4计算;侧墙根部由于水平土压力存在，同时需要进行抗剪承载力极限状态验算。底板构件除受弯外，同时受到侧向土压力引起的轴向力，故以压、弯为主，可简化为偏心受压构件，承载能力极限状态验算按照《公预规》5.3.4、5.3.6计算。

正常使用状态验算时，计算由作用频遇组合引起的开裂截面纵向受拉钢筋的应力σss时，侧墙（纯受弯构件）按《公预规》式6.4.4-2计算;底板（偏压构件）按《公预规》式6.4.4-4～6.4.4-8计算。同时，侧墙应视为大悬臂结构，需验算侧墙顶部的挠度值，可依照《公预规》第6.5.2条进行计算。

由于侧墙的存在，结构受力主要以横向水平土压力引起的弯压为主，此时，主筋受力方向为横桥向，随着侧墙高度降低，横向水平土压力降低，故主筋受力方向逐渐由单向受力转变为双向受力，建议U型槽与道路接驳处钢筋按照双向受力板配筋设计。

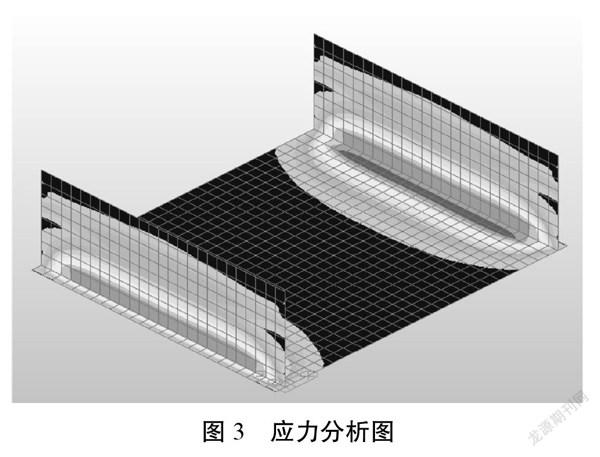
选取松江路下穿北京南路地道桥为例，通过对U型槽结构进行应力分析（如图3），可知在荷载组合作用下，侧墙受力最不利位置位于侧墙根部，底板受力最不利位置位于底板两侧及跨中车行道位置。

4.1 承载能力极限状态结果分析

在基本组合作用下，进行正截面抗弯承载力验算时，侧墙根部设计内力值为Mmax=2 228.9 kN·m（抗力为

3 223 kN·m），Mmin=452.6 kN·m（抗力为3 223 kN·m）;进行偏心受压承载力验算时，底板两侧设计内力值为Mmax=2 055.3 kN·m（抗力为2 800 kN·m），Mmin=407.6 kN·m

（抗力为2 800 kN·m），底板跨中车行道位置Mmax=

355.5 kN·m（抗力为1 438.9 kN·m），Mmin=205.9 kN·m

（抗力为1 438.9 kN·m）。

在基本组合作用下，进行斜截面抗剪验算时，侧墙根部受的最大剪力设计值为Vmax=719.2 kN（抗力为1 684.3 kN）。根据以上结果推论，U型槽结构的承载能力极限状态验算通过。

4.2 正常使用极限状态结果分析

在频遇组合作用下，进行使用阶段裂缝宽度验算时，得到侧墙根部最大裂缝0.144 mm，底板两侧位置最大裂缝0.163 mm。沭阳当地属于Ⅱ类-冻融环境，钢筋混凝土裂缝限值为0.2 mm。

在频遇组合作用下，侧墙结构端部最大水平位移值为16.4 mm，不超过规范中规定的最大限值H/300（H为侧墙高度）。根据以上结果推论，U型槽结构的正常使用状态验算通过。

5 結论

（1）进行U型槽计算时，应采用静止土压力计算水平土压力值，部分U型槽还需考虑结构外辅路上汽车荷载作用，此时汽车荷载为车辆荷载。基床系数取值在104～105 kN/m3）范围内的，可采用弹性地基梁法。

（2）通过对U型槽结构内力分析知，U型槽结构侧墙根部以及底板两侧为受力最不利截面。在承载能力极限状态下，两者的强度满足规范要求;在正常使用极限状态下，两者的抗裂性满足规范要求。同时，在正常使用极限状态下，侧墙顶的变形同样满足规范要求。

参考文献

[1]公路桥涵设计通用规范： JTG D60—2015[S]. 北京：人民交通出版股份有限公司，2015.

[2]袁聚云，等. 土质学与土力学（第四版）[M]. 北京：人民交通出版社，2009.

[3]顾晓鲁，等. 地基与基础（第三版）[M]. 北京：中国建筑工业出版社，2003.

[4]杨功勤. 地道桥结构静力与动力特性分析[J]. 工程建设与设计，2002（6）： 10-12.

[5]朱建栋，等. 地道桥结构与土相互作用的有限元分析[J]. 岩土力学，2004（11）： 305-309.

[6]公路钢筋混凝土及预应力混凝土桥涵设计规范： JTG 3362—2018[S]. 北京：人民交通出版股份有限公司，2018.

收稿日期：2022-01-13

作者简介：鞠炳照（1990—），男，硕士研究生，工程师，研究方向：桥梁与隧道工程。