高烈度区双层框架墩基础方案比选研究

摘要 受限于用地紧张及场地建设条件，双层框架墩在城市轨道建设中将得到广泛应用。文章以西安地铁10号线公轨合建段引桥30 m跨标准框架墩为例，对高烈度区两种基础方案进行比选，并进一步分析了整体式承台的受力规律。与整体式承台相比，分离式承台受力更明确、经济性更好;对整体式承台，建议先通过比较开裂弯矩与最不利工况的弯矩，判断截面是否开裂，再偏安全地采用考虑桩-土共同作用的土弹簧模型进行配筋设计。

关键词 高烈度;双层框架;整体式承台;分离式承台

中图分类号 TU375.1 文献标识码 A 文章编号 2096-8949（2022）06-0153-03

引言

随着我国经济社会的快速发展，交通拥堵已成为城市“痛点”。同时，城市土地资源日益紧张，征地拆迁和施工组织的难度增大，进一步制约了交通效率的提升。为节约线位资源，提高土地利用率和交通运输效率，复合通道应运而生。目前，复合通道在我国城市轨道交通中的应用较少，已通车的有上海闵浦二桥、菜园坝长江大桥、朝天门长江大桥、东水门长江大桥。可预见，作为一种集约化的交通模式，复合通道在城市轨道建设中将得到广泛应用。

经调研，国内公轨合建桥引桥大多采用双层框架墩，且主要位于低烈度区。对高烈度区双层框架墩，相关研究和应用较少。因此，有必要开展相关研究，指导该类地区同类型结构的设计。

1 工程概况

西安地铁10号线公轨合建段引桥上层为六车道快速路，下层为轨道10号线。该区域引桥地震动峰值加速度值为0.2 g，抗震设防类别为重点设防类，抗震设防烈度为8度。

引桥上层采用30 m钢混叠合连续梁;下层受限于运输条件，采用双线简支现浇箱梁。上层盖梁采用预应力混凝土结构，跨中梁高2.2 m，混凝土等级为C50;下层系梁采用钢筋混凝土结构，跨中梁高2.2 m，混凝土等级为C50;墩柱间距14 m，尺寸为2.5×2.4（纵×横）m，混凝土等级为C50;整体式、分离式承台尺寸分别为18.1×6.9×3.2（纵×横×厚）m、8×8×3.2（纵×横×厚）m，混凝土等级为C40;桩直径为1.5 m，混凝土等级为C35。

根据初步设计成果，上层快速路采用HDR系列高阻尼隔震橡胶支座，下层轨道采用摩擦摆减隔震支座。

2 不同基础方案比选

双层框架墩通常采用两种基础方案：整体式承台、分离式承台。整体式承台优点是整体刚度大、工后沉降小，缺点是受力机理复杂、适应性差;分离式承台受力机理明确、适应性强，缺点是整体刚度略小，当横向地质差异大、荷载不对称时，工后沉降差异大。下面将对这两种方案进行同深度比选，供同类工程参考。

2.1 模型的建立

采用Midas Civil建立双层框架墩的有限元模型（见图1、2）。构件均采用空间梁单元模拟，桩-土共同作用采用一般弹性支承的刚度矩阵模拟。

2.2 整体式、分离式承台方案对比

除承台尺寸不同外，其余构件尺寸均相同。分离式承台考虑5 mm横向墩台沉降差。

地震工况下，两种方案的结构动力结果见表1。由表可见：

（1）纵向地震作用下，分离式承台控制截面的弯矩比整体式承台对应的弯矩略大。

（2）横向地震作用下，分离式承台下层墩柱的柱底弯矩比整体式承台对应的弯矩减小约20%，影响显著。

（3）纵向地震作用控制墩柱配筋设计。

根据《规范》[1]，计算得左、右墩台沉降差为0.1 mm，远小于假定的墩台沉降差。可见，分离式承台方案工后沉降差异较小。

圖3反映了两种承台方案材料用量的差异。可见，整体式比分离式方案钢筋用量略高，混凝土用量反之。经测算，整体式比分离式方案材料费贵6.3万元，即：分离式承台方案更经济。

3 整体式承台配筋设计

目前，试验和理论研究[2-3]发现，承台部分为应力扰动区（D区），建议采用拉压杆模型进行配筋设计。规范[4]的公式适用于墩柱位于承台中心的情况，对墩柱偏心布置的整体式承台的适用性有待商榷。因此，有必要建立实体有限元模型，研究这类承台的传力机理，为配筋设计提供依据。

3.1 模型的建立

采用FEA NX建立实体有限元模型（见图4）。按圣维南原理，墩柱高度取3 m;按《规范》[1]，桩长取hm=2（d+1）=5 m。忽略桩-土共同作用，桩底固结。柱顶采用共用节点，施加柱的内力，内力值由考虑桩-土共同作用的土弹簧模型（见图5）提供;承台顶采用压力荷载施加土压力。墩柱、承台、桩基采用3D混合网格自动划分，钢筋采用1D网格自动划分，自动网格划分尺寸均取0.2 m。混凝土和钢筋单元自动耦合。

3.2 整体式承台的受力规律

图6为承台不同位置处的混凝土应力分布图。可以看出，在荷载作用下，承台跨中、距跨中1 950 mm处，承台横向混凝土应变基本满足平截面假定，受力接近一般受弯构件;墩柱内侧处承台横向混凝土应变不满足平截面假定，受力接近深梁构件。

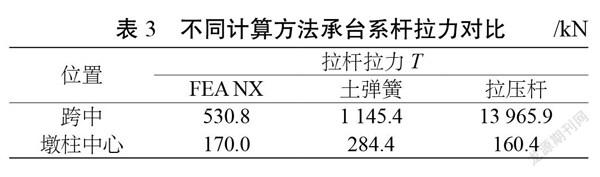
3.3 不同计算方法系杆拉力对比

承台顶、底层横桥向分别通长布置110  32、110  28。

基于刘运林[5]的研究成果，承台跨中处的开裂弯矩计算值与最不利工况的弯矩值的对比见表2。由表可知，承台跨中处的开裂弯矩大于最不利工况的弯矩，即：跨中未开裂。

因规范[4]的公式无法考虑整体式承台跨中上缘横向受拉的情况，故有必要根据精细化模型揭示的受力规律，构建新的拉压杆模型（见图7）。

由表3可以看出，土弹簧模型的拉杆拉力计算值高于FEA NX模型的计算值，偏安全;拉压杆模型墩柱中心处的拉杆拉力计算值与FEA NX模型的计算值接近，但其跨中处拉杆拉力计算值远大于FEA NX及土弹簧模型的计算值，其结果可能失真，即：该文的拉压杆构形不是最优构形，不能最真实地反映承台的力流传递机理。

4 结论

（1）横向地震作用下，除潜在塑性铰（上层墩柱柱顶、下层墩柱柱底）外，两种基础方案其他控制截面的弯矩差异较小，采用分离式方案可显著减少下层墩柱柱底的面内弯矩。

（2）对高烈度区双层框架墩，分离式承台受力机理更明确、适应性更强、经济性更好。

（3）整体式承台进行配筋设计时，建议通过比较控制截面开裂弯矩与最不利工况的弯矩，判断截面是否开裂。

（4）土弹簧模型可用于整体式承台的配筋设计，且偏安全，而拉压杆模型受限于传力机理复杂，构形不唯一，其适用性有待进一步研究。

参考文献

[1]铁路桥涵地基和基础设计规范： TB 10093—2017[S].北京：中国铁道出版社有限公司， 2020.

[2]Adeber P.， Kuch ma D.， Collins M.P. Strut and tie  models for the design of pile caps： an experi mental study. ACI Structural Journal，1990（1）：81-92.

[3]卢建峰. 桩基承台空间桁架理论设计方法研究[D]. 南京：东南大学， 2001.

[4]城市轨道交通桥梁设计规范： GB/T 51234—2017[S].北京：中国建筑工业出版社， 2017.

[5]刘运林， 储德华， 刘建军， 等. 钢筋混凝土梁开裂荷载计算公式比较研究[J]. 建筑结构， 2015（6）：14-17.

[6]水工混凝土结构设计规范： SL 191-2008[S].北京：中国水利水电出版社， 2009.

[7]ACI Co mmittee 318. Building Code Require ments for Structural Concrete and Co mmentary（ACI 318-19）[S]. A merican Concrete Institute， 2019.

收稿日期：2022-02-23

作者简介：谢俊龙（1988—），男，硕士研究生，桥梁设计师，从事桥梁设计工作。