巧用数形结合，让数学教学更有效

陈丽惠

数形结合是一种重要的数学思想，它可以使知识的呈现直观形象，化繁为简、化难为易，从而帮助学生掌握知识、发展思维、提高能力。

一、巧用数形结合，让概念教学更有效

数学概念是现实对象的空间形式和数量关系的本质特征在大脑中的一种反映形式，具有高度的概括性与抽象性。因此，教师要巧用数形结合，借“形”来呈现概念所描述的数学知识，将抽象的文字具体化，让学生在对“形”的感知中建立表象，从而掌握数学概念的本质特征，构建清晰的数学概念。

教学人教版三上“分数的初步认识”一课。当单位“1”是一些物体时，学生对用分数表示部分与整体的关系感到不适应。教学中，要精心设计教学环节，巧用数形结合让学生循序渐进地体会到当单位“1”是一些物体时该如何用分数表示整体与部分的关系。

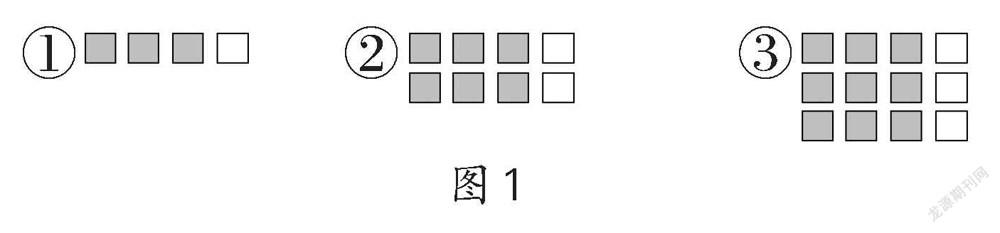
教学例1时，笔者设计用数表示图中的涂色部分的环节。①出示 ，用几表示？（用1表示）②出示 ，变成 ，用几表示？（用3表示）③如果再出现一个该用几表示？（学生答4后，出示 ，组成       ）

笔者：“用几表示？”生1：“用3表示。”筆者：“第4个就不算了吗？”生2：“用[34]表示。”笔者：“有不同想法了，你是怎么想的？”生2：“一共有4个，涂色部分占3个，可以看成平均分成4份，取其中的3份。”笔者：“思路很清晰，解释很到位。继续，请用分数表示你看到的涂色部分。”（逐一出示图1）学生反馈大多为[34]、[68]、[912]。笔者：“有不一样的吗？”生3：“我只写了[34]。我是竖着看的，这样就都可以看成平均分成4份，取其中的3份，所以都可以用分数[34]来表示。”笔者操作课件，在图形中加上虚线，将它们平均分成4份，接着说道：“它们都可以用分数[34]来表示。那如果再来一组呢（横向增加一行方块），用哪个分数表示？再来10组呢？图中方块的数量一直在变，什么不变？”生4：“都平均分成4份，取其中的3份。”笔者随即指出可以把这些图形看作“一个整体”。

之后，笔者设计一个核心问题：“6个苹果”或“[12]张纸”可以看作“一个整体”吗？一方面帮助学生理解“一个整体”可以很大也可以很小;另一方面引导学生重点思考“分的对象是什么”“平均分成几份”及“取出几份”，体会分数部分与整体含义中的关键要素，深化对分数本质属性的认知。

二、巧用数形结合，让计算教学更有效

教学中，有些教师会侧重指导学生掌握计算的方法，却忽视了对算理的理解，这种教学形式往往无法获得较好的效果，也难以真正发展学生的数学思维。教学时，教师要巧用直观图，把数与形对应起来，引导学生细心观察，充分交流自己的想法，构建计算方法模型，实现对算理的理解。

教学人教版六上“分数乘分数”一课。学生根据题意列出算式[12]×[15]和[12]×[35]并不困难，对于计算却无从下手。笔者让学生拿出一张长方形纸，先折出长方形纸的[12]并涂色，再与同桌分工分别折出[12]张长方形纸的[15]和[35]，并用斜线表示出来。

第一层次：观察图形，理解

算理（展示学生作品，图2）。

笔者：“图中的涂色部分都表示长方形纸的[12]，画斜线的部分各占[12]的几分之几？”生：“画斜线的部分各占[12]的[15]和[12]的[35]。”笔者：“那[12]的[15]和[12]的[35]又各占这张纸的几分之几？小组内讨论一下。”在学生回答时，笔者注意引导他们理解并说清“谁是谁的几分之几”：[12]的[15]，是以[12]为单位“1”，把它平均分成5份，取其中的1份。但以整张长方形纸为单位“1”进行观察，就可以发现[12]的[15]占了长方形纸的[110]。这样，就把几分之几乘几分之几转化成1乘几分之几了，也就是把[12]的[15]转化成1的[110]，算理清晰，计算答案也就水落石出了。用同样思路引导学生理解[12]×[35]=[310]。

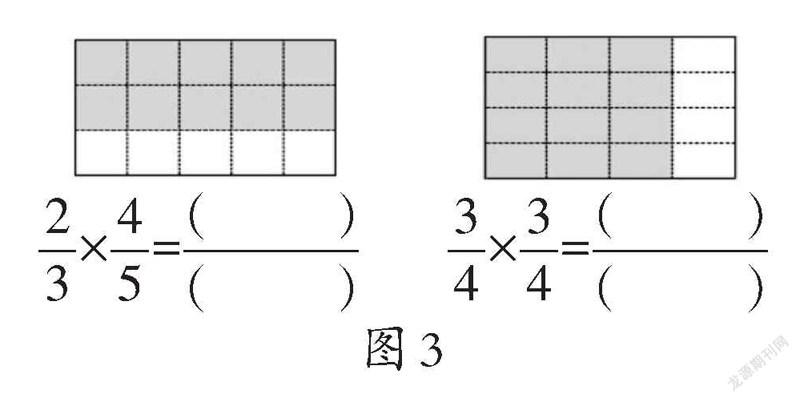
第二层次：根据算式，画出图形（学习单与课件

呈现，图3）。

笔者：“你能在图中画斜线表示结果再填空吗？与同桌说一说‘谁是谁的几分之几’。”

第三层次：观察“数形”，梳理算法。

笔者提出：“经过上面的两个环节，你有什么发现？”学生小组交流后总结：分数和分数相乘，用分子相乘的积作分子，用分母相乘的积作分母。

通过以上三个层次的数学活动，由简单到复杂，让学生在探索和理解分数乘分数算理的基础上，发现并总结出分数乘分数的计算方法。可见，数形结合的直观性既可以使学生体会到数学的趣味和奇妙，又可以将枯燥的数学计算变得生动形象，易于理解与掌握，让课堂教学更有效。

三、巧用数形结合，让解决问题更有效

在解决问题的教学实践中，适时巧用数形结合思想，把抽象的问题放在直观的情境中，帮助学生把复杂的问题简单化、抽象的问题形象化，学生就能更容易理解各种数量之间的关系，从而提高应用所学知识解决问题的能力。

教学人教版一上“排队问题”。小军前面有9人，后面有5人，一共有多少人？大部分学生列式9+5=14（人）。笔者：“听说同学们个个都是画图高手，能不能请你们用简便的图形把题意表示出来？小组里先讨论，再动手画。”于是就有如下示意图（图4）。观察示意图后，学生恍然大悟，便修改算式为9+1+5=15（人）。

这时，笔者趁热打铁将题目稍微改动：从前往后数，小军排在第9位，从后往前数，小军排在第5位，这一队一共有多少人？有了上一题学习方法的借鉴，学生马上动手画示意图，出现了2种解决方案：9+5-1=13（人），8+4+1=13（人），如图5、图6所示。

显然，借助示意图来分析题意，形象直观，既可以帮助学生理解题意和解决问题，又可以让学生感受到画图策略的重要性，是渗透数形结合思想的重要手段之一。在教学过程中，教师要让学生养成画图思考的好习惯，感受数形结合思想的优点，从而提高学生的数形相互转化能力，实现数形互助互补，提高教学有效性。

（作者单位：福建省厦门市翔安区教师进修学校附属小学）