思考表达，感悟道理

叶育新

贵州师范大学吕传汉教授倡导的“数学三教”，即教体验、教思考、教表达，提倡在学习的过程中让学生充分经历体验、思考、表达的过程，从而达到长见识、悟道理的目的。笔者认为，体验、思考和表达是儿童学习数学层层递进的过程，其中体验是学习的基础，思考是思维的内隐形式，表达是思维的外化形式，而说理是表达的一种重要形式。下面，笔者结合自己的课堂实践与观察，就引导学生感悟数学道理谈几点教学思考。

一、在操作活动中感悟数学道理

1. 在探索性操作中感悟数学道理。

动手操作是重要的学习活动之一，在探索知识的操作中要注意操作与思维相结合，让学生带着问题进行思考，在思考中感悟数学道理。“平行四边形的面积”一课，在通过剪拼平行四边形探索面积公式的过程中，会产生问题：怎样剪才能拼出一个长方形？教师可以让不同的学生演示操作过程，结合观察进行说理，发现只有沿着高剪开才能将平行四边形剪拼成一个长方形。教师可以追问：“为什么只有沿着高剪开才能剪拼成长方形呢？”通过进一步说理让学生认识到：因为沿着高剪开会产生直角，而长方形有四个直角。进而感悟到：如果不沿着高剪开，就不会产生直角，也就拼不出长方形。在上述过程中，学生的操作探索是一种体验，而认识到“沿着高剪开才能拼成长方形”则是基于体验基础上转化的经验，当然，这种转化需要经历对真实问题的思考和说理才能实现。

2. 在开放性操作中感悟数学道理。

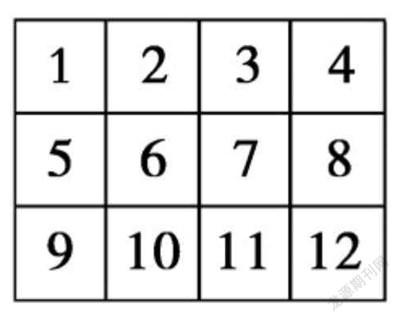
有些问题的操作方法不止一种，教师要注意引导学生在比较不同的操作中思考共性特征，感悟数学道理。在四年级学习了长方形周长后，教师可以设计一道开放型的操作说理题：如图所示，在一个由12个小正方形拼成的大长方形中取走一些小正方形，大长方形的周长会变吗？可结合操作呈现不同方法，并思考其中的共同道理：只要从大长方形四个角的位置上取走小正方形（1、4、9、12），周长不变。在此基础上，教师可以进一步提出问题：如果要保持周长不变，最多可以取走几个小正方形？可让学生结合分步操作，尝试进行说理。如先从4个角取走4个小正方形，再思考：①如果再取1个小正方形（共取走5个），应怎么取？（可取2、3、10、11中的某一个）②如果要再取走1个小正方形（共取走6个）应怎么取？（可取2和10、2和11、3和10或3和11）③不同取法有什么共性呢？可通过对上述问题的说理让学生明白，取走长方形后，要保证消失的边能在新的图形中“长”出来，使得外輪廓中水平方向的边之和保持8格，垂直方向的边之和保持6格，就能使周长保持不变。

二、在运算学习中感悟数学道理

1. 在算理辨析中深度思考，感悟道理。

在运算教学中要注意算法和算理并重，让学生不仅要掌握算法，更要通过辨析展开深度思考，明白算理。如“异分母分数加减法”的教学，教师出示例题[14]+[25]，让学生尝试计算，学生可能呈现两种典型算法，算法一是将分子分母分别相加得出结果[13]，算法二是先通分，将两个异分母加数分别转化成同分母分数后计算得出结果[1320]。由此产生问题：到底哪种算法正确？教师可鼓励学生各抒己见，展开辩论，用不同的方法证明自己的观点。可让学生通过折纸或画图，体验两个分数相加的过程。通过观察和比较，感悟到在算法一中，和[13]比加数[25]还小，显然不符合逻辑，教师应注意让学生发现并说出这个逻辑思考过程，排除错误算法。对算法二的判断和说理可以分为两个层次：①为什么要通分？可结合图示展现通分的过程，让学生结合观察进行说理，感悟到通分的实质是把两个异分母加数转化成相同计数单位的分数;②比较分数加减法和小数加减法、整数加减法的计算法则有什么异同，通过说理比较，让学生感悟到，虽然算法不同，但是算理相同，都是相同计数单位相加减。

2. 在算法比较中把握共性，感悟道理。

在简便计算中，很多算式都有不同的算法，教师要引导学生进行比较思考，通过说理优化算法，形成策略。如计算0.125×8.8，学生可能有三种简便算法：算法一，0.125×（8+0.8）;算法二，0.125×（9-0.2）;算法三，0.125×8×1.1。教师要注意让学生说清思路和算法，并进行比较。如算法一和算法二都是先用分解法，再运用乘法分配律进行简算，但算法二不如算法一简便。算法三也是运用分解法把8.8分解成8×1.1，这是最简便的方法，但学生不容易想到。教师可启发学生思考：上述方法中有哪些相同之处，你最喜欢哪一种，你认为哪一种最简便，请说出理由。让学生感悟到：这三种简算方法虽不相同，却都用到了共同的策略——数的分解。8.8的分解要和0.125的数据特征相对应，应尽可能分解出与8相关的数，才能实现简算。当然，教师还可以做进一步拓展，把算式中的0.125替换成2.5，问学生：如果是2.5×8.8，你会怎么简算，简算中对数据的拆分要遵循怎样的共同原则？让学生通过说理进一步体会简算策略，即数的分解要符合数据特征。

三、在策略反思中感悟数学道理

数学游戏是激发儿童学习情感的重要形式，在游戏的过程中应该重视策略分析与反思。笔者曾经设计一个数学游戏：一堆棋子共25枚，甲乙二人轮流从中拿取，每人每次最多取4枚，最少取1枚，谁拿到最后一枚棋子谁胜。要怎么拿才能确保获胜？第一环节可以设计成教师和男生进行对抗赛，让男生先取，教师后取。第二环节可设计成教师和女生进行对抗赛，让女生先取，教师后取。当学生发现每次都是教师获胜时，适时激发学生思考：为什么每次都是教师取胜？为什么后取容易获胜？通过还原取数过程，组织学生观察、讨论并说理，让学生明白：以1+4=5为一轮，如果学生先取，不管第一个取多少，每一轮教师所取棋子数和学生取的棋子数相加之和都应保证是5，就能获胜（最后一轮教师可根据实际情况分别取1、2、3、4个）。在此基础上，教师可改变总数，问学生，如果棋子总数为27，游戏规则不变，要想赢，应该怎么取数？请讨论并说明其中的道理。让学生感悟到：这种玩法模型其实可以归纳为有余数除法算式27÷（1+4）=5……2，要想取胜，先要把余数取掉，如第一次教师先取2枚，以后每次教师取的棋子数和学生取的棋子数相加的和是5，就可以取胜。最后教师可以让学生应用本游戏中蕴含的数学道理设计一个类似的数学游戏并说明取胜原理。

（作者单位：福建省福州市鼓楼区教师进修学校 本专辑责任编辑：王彬）