拖体惯性类水动力系数快速计算方法

陈小星 洪有财 胡勇军

（第七一五研究所，杭州，310023）

海洋拖曳设备广泛应用于军事、勘探、救援等领域。拖曳设备的水动力特性对其稳定性、释放回收、空间布局均具有重要影响，同时也是进行六自由度空间运动分析与运动控制的前提和基础。而水动力系数是表征拖曳设备水动力特性的有效定量参数，因此获取精确的水动力系数对拖体的设计具有重要意义。水动力系数的获取一般是通过模型试验，在拖体设计阶段，往往需要多次调整拖体线型，对每一次线型调整均制作模型是不现实的。随着计算机技术的飞速发展，数值仿真计算被广泛采用。

高峰给出了潜器惯性类水动力参数计算方法[1]，对常用的计算方法进行了总结，并采用基于势流理论的Hess-Smith面元法进行编程求解计算。张赫给出了潜水器水动力系数计算方法[2]，并使用近似公式计算、面元法和 Fluent模拟循环水槽仿真计算。采用面元法需利用其他 CAE软件对模型进行网格划分，并编写软件读取网格数据、求解计算、可视化后处理，其编程过程复杂且求解效率低。

本文采用COMSOL软件内置的PDE模式，直接对拉普拉斯方程进行求解，采用COMSOL边界元法为数值计算方法，使用其内置的高效、并行求解器进行求解，避免复杂繁琐的编程工作，并基于软件进行了二次开发，可以对各种模型实现快速求解计算，大大提高了工作效率。

1 数值模型

计算惯性类水动力系数时，一般考虑流体为理想流体，忽略粘性作用，在惯性坐标系下，流体的连续性方程[3]如下，其中φ为速度势。

物体表面的边界条件为物体与流体的法向速度相等：

式中，n为拖体表面的法向方向。令拖体的平动速度为 u，绕拖点的旋转角速度为ω，r为从拖点出发的位置向量。则拖体表面的速度为

记附加质量为[4]

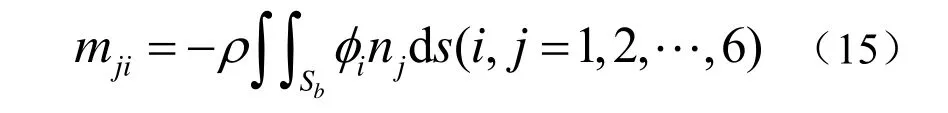
由势流理论[4]可知，附加质量与惯性水动力系数数值相等，符号相反。依据上述模型，采用边界元法，分别施加6个单位速度ui，求出单位速度势，并利用式（15）对拖体表面进行积分即可算出惯性类水动力系数。

2 计算方法

选择物理场为数学模块中的边界元偏微分方程建立稳态研究。导入拖体的三维模型，建立无限空域模型，因变量为速度势iφ。分别添加6个通量边界条件ni，见表1。

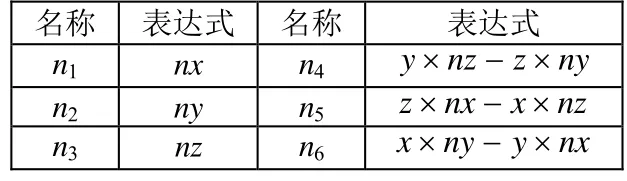
表1 ni定义表

定义积分耦合算子intop1，对拖体表面的速度势进行积分。水动力系数变量见表2，其中rho为水密度。

表2 水动力系数定义表

为验证模型计算的有效性和计算精度，建立了圆球网格模型，比较不同网格数量对计算精度的影响。其理论附加质量计算公式为

式中，ρ为水密度，取1000 kg/m3；R为圆球半径，取0.5 m。上式计算结果为261.799 4 kg。

采用不同的网格数量比较计算结果精度，网格数量为350的圆球网格模型见图1，其不同网格大小的计算结果见表 3。可见计算精度随着网格数量的增多而不断提高。且其计算精度与理论值相比误差远小于 1%，计算精度良好，完全满足工程应用需要。

图1 圆球网格模型（网格数量350）

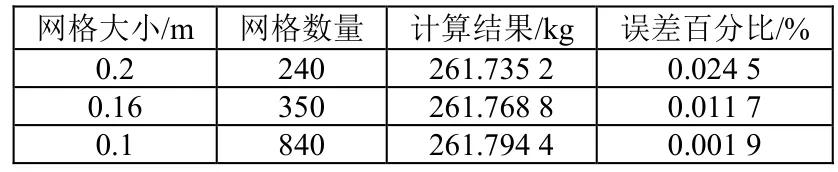
表3 网格大小计算结果

3 计算结果分析

根据圆球网格数量验证的结果对拖体进行网格划分，采用与圆球网格划分数350同样的网格划分方法。拖体表面进行网格划分，单元大小选择“细化”，划分网格如图2所示。网格总共数量为9846。

图2 拖体网格示意图

针对不同的通量边界条件ni分别建立6个稳态，分别求解计算。以n1、n4态运动为例，单位速度势分布如图3～4所示。

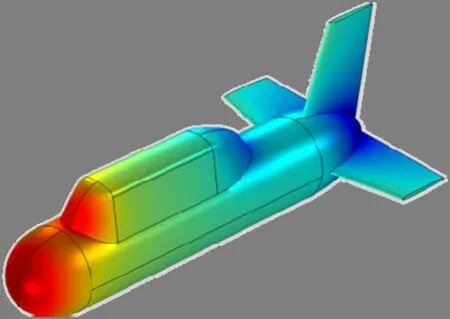
图3 n1态运动单位速度势分布图

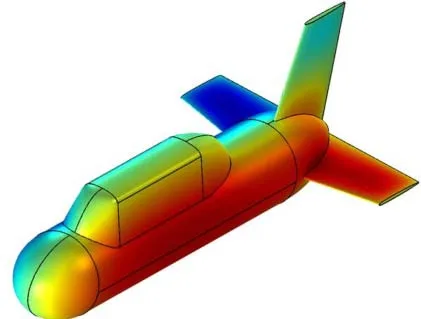
图4 n4态运动单位速度势分布图

按表2对拖体表面用积分算子进行积分获得惯性类水动力系数，如表4中仿真值列所示。将计算结果与进行平面运动机构水动力测试的实验值进行比对，可知各水动力系数误差均较小，均能与结果较好吻合。由于该计算方法基于势流理论，没有考虑到流体的粘性力作用，会带来一定的计算误差。考虑到拖体运动一般为缓慢变化运动，其加速度值本身相对较小，对拖体姿态的影响也较小，误差10%左右可以满足工程使用的精度要求。

表4 水动力系数比对图

4 APP二次开发

拖曳式的水下拖体类设备的设计具有普遍性，均包含流线型拖曳体以及水平或垂直平衡机翼。在拖体的设计过程中，需要对惯性类水动力系数进行计算并根据计算结果修改拖体的线型。拖体线型的修改同时影响内装件的布置，因此往往需要经过多次迭代才能完成拖体设计。借助于COMSOL的二次开发功能，我们开发了一种可用于拖体惯性类水动力系数计算的标准快速算法，可缩减拖体设计过程中的水动力系数反复仿真计算时间，提高拖体设计效率。

COMSOL的二次开发界面完整集成于软件界面内，通过APP开发器建立表单，并插入“文件导入”、“数据显示”、“图形”、“按钮”等对象，APP界面如图5所示。通过“文件导入”对象可以导入不同的模型，导入后重建几何体，划分网格完成后即可进行计算。计算完成后，通过“数据显示”对象可显示不同的水动力系数值，并在右侧通过“图形”对象显示模型计算云图。通过该APP可大大缩减整个仿真计算的时间。

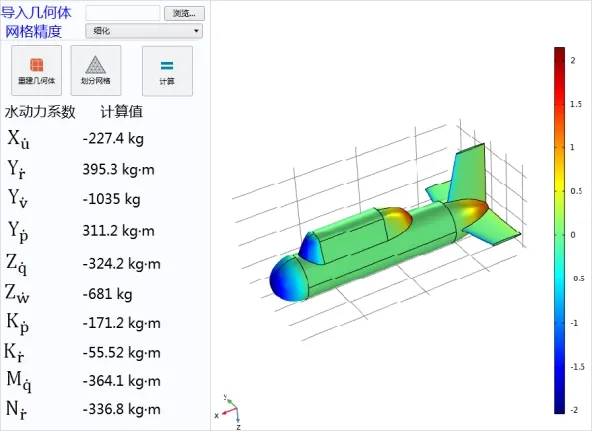
图5 水动力系数计算表单

5 结论

本文采用势流理论，建立了基于COMSOL软件二次开发技术的惯性类水动力系数计算模型，结果与模型实验值吻合良好，能够较精确的预报惯性类水动力系数。该方法求解迅速，计算精度高，适用性广，为水下潜器的惯性类水动力系数预报评估提供了一种快速且有效的求解新途径。