基于波束形成原理的ADCP海浪波向估计方法

康恺 王忠康

（第七一五研究所，杭州，310023）

海浪观测分析及预测预报、海洋环境研究以及海洋船舶工程等领域都需要研究海浪谱。海浪方向谱观测手段按照测量方法可以分为人工观测法、仪器测量法和遥感反演法。人工观测法准确度和观测水域受到限制；仪器测量法通常使用声学仪器进行测波，能够进行水底和水面的测量，且观测连续性较好；遥感反演法主要利用雷达测波和卫星测波，观测成本较为昂贵[1]。声学多普勒流速剖面仪（Acoustic Doppler Current Profiler，ADCP）测波时可安装在水下或是海底，避免了海面大风浪对观测系统的破坏，具有测量准确度高、操作简单的特点。因此对基于ADCP波向估计方法的研究具有显著的理论与应用价值。海浪方向谱描述了一个组成波在频率和角度上的分布，而海浪可以看作是多个随机相位组成波的叠加。海浪交叉谱表示任意两个海浪特性在频率上的相关程度。任意两个海浪特性间的交叉谱等于海浪特性与海面间的传递函数与海浪方向谱乘积的傅里叶变换，使用反演算法可以估计海浪谱[2]。

Barber最早提出基于波高仪阵列测量海浪方向谱的算法，该方法通过直接傅里叶变换（Direct Fourier Transformation，DFT）对海浪谱进行了估计，运算速度快，可初步了解海浪分布情况，但方向分辨率不高[3]。Capon提出了最大似然法，相比于DFT法，精度有一定提升且估计速度较快，是目前工程中比较常用的算法[4]。Hashimoto等人提出了贝叶斯法是目前估计精度最佳、最稳定的算法，但是计算量过大[5]。以上方法大都通过测得的多个海浪参数（如海面高度、海面垂直速度、海面坡度、水质点速度等）间的互谱来估计海浪方向谱。

受阵列信号处理中利用波束形成估计来波方向原理的启发，本文提出了基于波束形成的海浪方向估计方法。波束形成方法核心是对于阵列信号加权求和后把方向增益集中，形成一个波束，通过调整加权矢量让期望信号输出功率最大，此时的波束方向即作为来波方向的估值。在估计海浪谱中，利用波束形成方法可以将海浪在传播过程中到达ADCP采样点时产生的时延差用于估计波向。

1 海浪模型与ADCP波向估计原理

1.1 海浪模型

海浪方向谱描述了海浪在频率和角度上的分布情况，一般可以假设方向分布与海浪的频率分布无关，海浪方向谱表达式为[6]

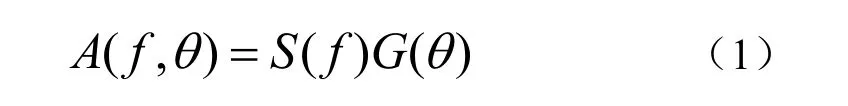
式中，S(f)为海浪频谱，G(θ)为海浪方向分布函数。常用海浪频谱模型是PM（Pierson-Moscowitz）谱：

式中，α=8.1×10-3，β=0.74，αg2=0.78，U 是海面上19.5 m高处的平均风速。式（2）中的海浪频谱仅含一个参量U。海浪频谱的0阶矩为

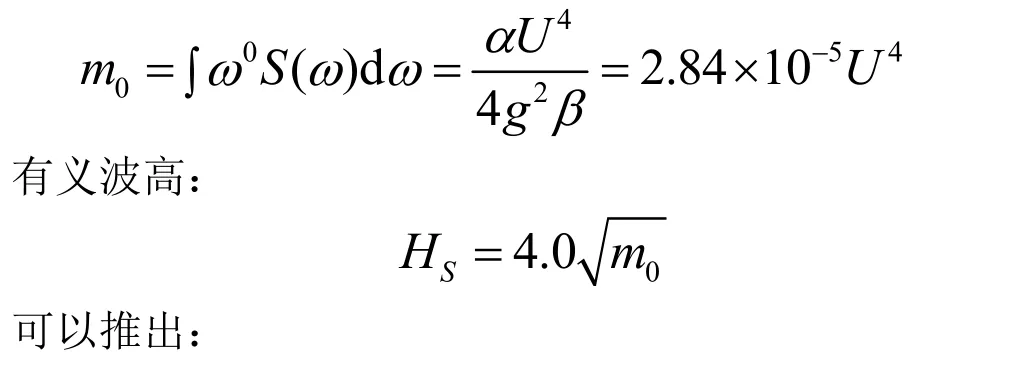
图1为PM谱仿真得到海浪频谱分布模型。

图1 海浪频谱S(f)

海浪方向分布函数的简单经验公式为

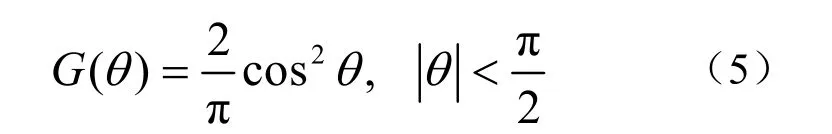
海浪方向分布函数如图2所示，峰值处为波浪传播主波向。

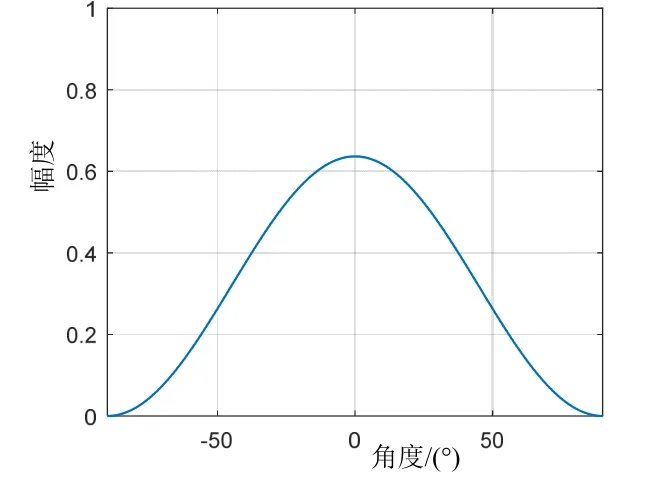
图2 海浪方向分布函数G(θ)

目前已有的海浪模型是利用海浪频谱和方向函数得到组成波，再根据随机波动理论叠加得到模拟三维海浪平面。

1.2 ADCP波向估计原理

ADCP是一种利用多普勒效应的测流仪器。在测量中，ADCP以一定的频率发射信号，这些信号在传播过程中发生反射，根据回波强度可估计海面高度[7]。ADCP坐底测量海浪的采样示意见图3。以ADCP为原点建立坐标系，使用四个倾斜波束和一个垂直波束可获得5个点的海面高度测量数据。使用互谱反演算法处理测量得到的五组海面高度数据可以得到海浪主波向的估计值。

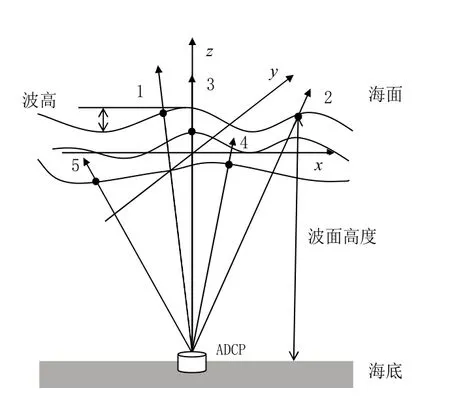
图3 ADCP空间采样示意图

空间采样要求采样点间距≤最小波长的1/2。通常，海水中海浪频率与波数的关系为[8]

式中，d表示水深，g为重力加速度。又因为ω=2πf和 λ=2π/k，且根据海浪波速 c=λf=ω/k，可将式（6）改写成海浪波长λ与海浪频率f的形式：

在水深d=50 m的条件下，波长>100 m为浅水环境，波长≤100 m为深水环境。ADCP发射波束与垂直方向成20°的夹角，可以推算出5个波束打到海浪平面上，大致的坐标点为（±12，±12）和（0，0）。根据式（6），绘制在水深d=50 m条件下的海浪频率与波长之间的关系曲线，如图4所示。由图可知，在被测波<0.21 Hz的典型水深条件下，海浪长度符合空间采样要求。

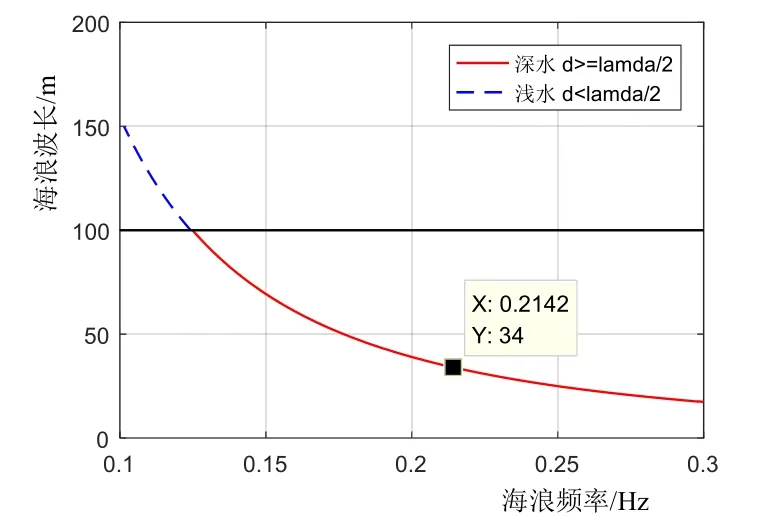
图4 水深d=50 m条件下海浪频率与海浪波长的关系

2 基于波束形成的波向估计方法

鉴于海浪波向估计与传感器阵列波达方向估计[9]的相似性，本文将波束形成应用于海浪波向估计领域，提出了利用波束形成估计波向的方法。

假设第M个空间采样点接收海面高度信号为

式中，Ri表示ADCP测量得到海面高度的协方差矩阵。由式（11）可知，此时输出功率最大，峰值处对应角度即为估计波向。

使用常规波束形成（Conventional Beamforming，CBF）估计波向，可以推出角度分布上最大输出功率为

MVDR（Minimum Variance Distortionless Response）波束形成原理是在保证主波向上的信号输出为一个常数条件下，使阵列的输出功率极小化，可以表示为

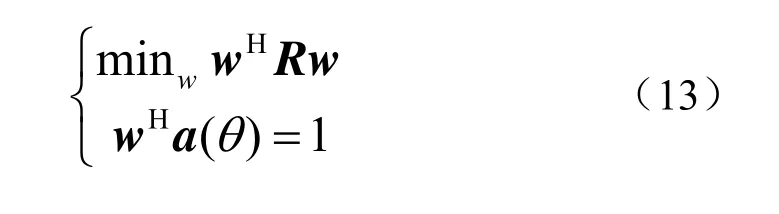
对于使用 MVDR波束形成估计波向，得出输出功率的角度分布为

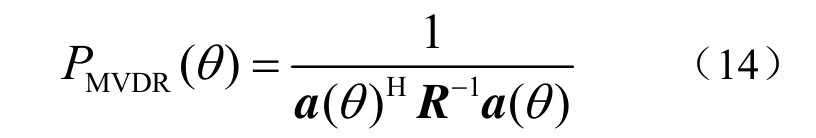
利用波束形成估计波向的流程图见图5。

图5 波束形成法估计海浪波向流程图

3 建模与验证

通过建立三维动态海浪模型，采集5点处的海面高度数据进行处理。利用波束形成法对波向进行估计。

3.1 三维海浪建模

仿真可将海浪平面看作多个不同初始相位组成波的叠加，在假设单峰分布情况下，海面上任意一点在某一时刻的高度为

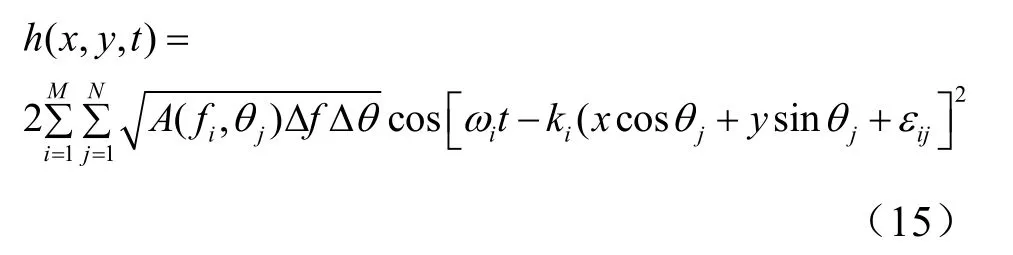
式中，M表示频率分割数，N表示角度分割数，εij为随机相位，范围在（0，2π）内，A(fi,θj)由式（1）确定。

仿真取海面以上19.5 m处、风速8 m/s的PM谱和主波向为 50°的方向分布函数，代入式（15）生成三维海浪平面。仿真条件如表1所示。将得到的海浪方向分布函数和海浪频谱模型相乘，得到海浪方向谱，如图6所示。

图6 海浪方向谱仿真结果

表1 三维海浪模型参数

假设水深d=50 m，以ADCP放置位置为原点建立如图3所示的坐标系，根据波动理论建立三维动态海浪平面，如图7所示。另外，仿真了5波束处海面高度测量结果。ADCP采样时长为500 s，采样间隔1 s，得到的分点海面高度如图8所示。

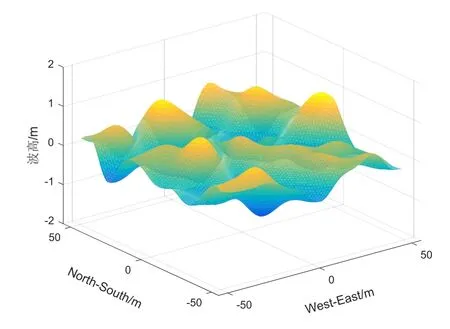
图7 某一时刻海面高度仿真结果

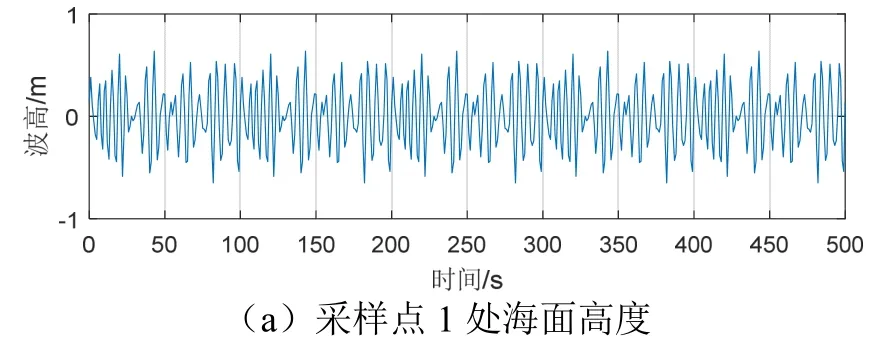
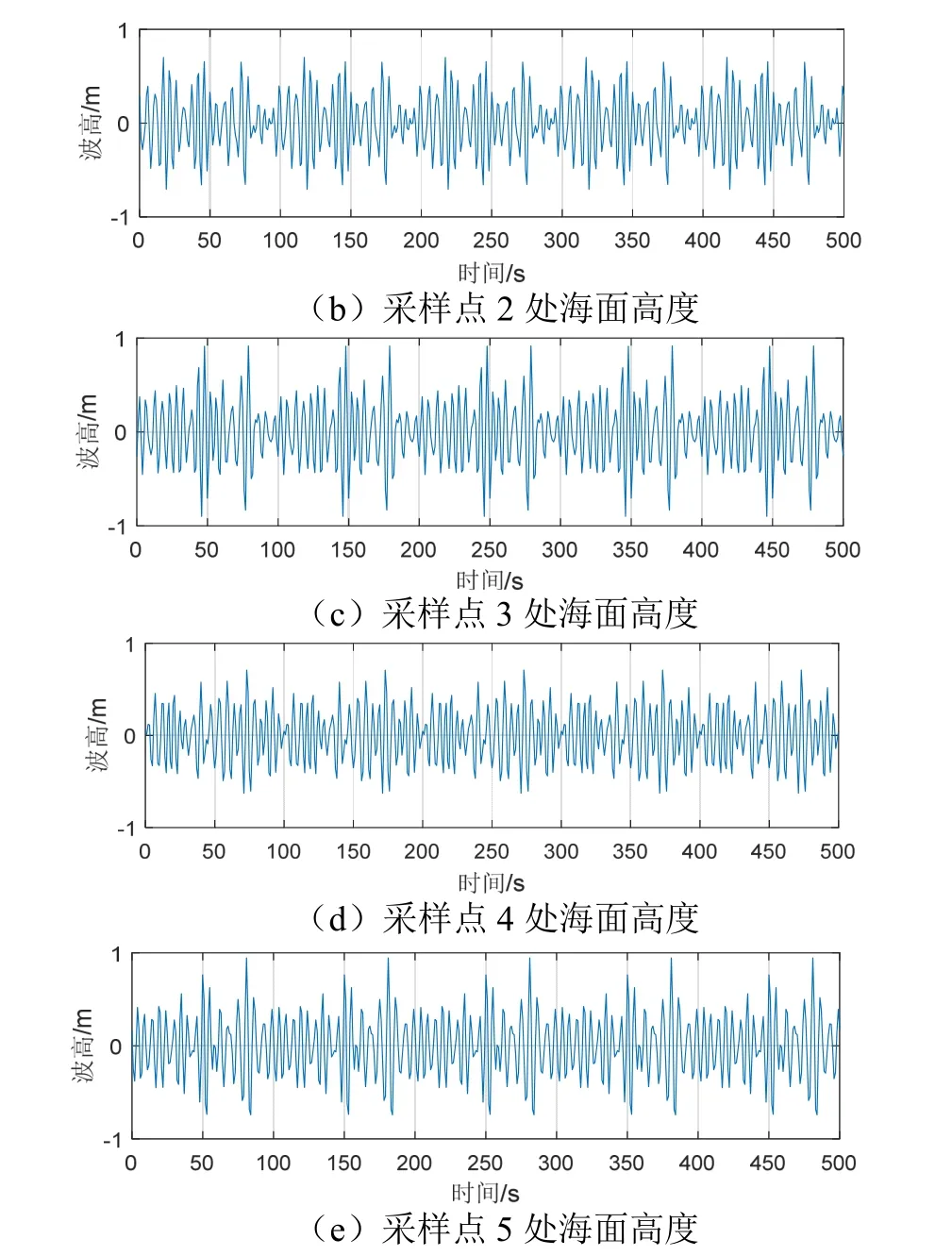
图8 海面高度随时间变化仿真结果

根据仿真得到的动态海浪三维模型，对每个采样点位置处的海面高度进行记录。波高可定义为上跨零线一侧显著波峰与另一侧显著波谷间高度差[6]。通过上跨零点法统计每一个采样点处有效波高HS，平均波高和平均波周期，统计结果如表 2所示。根据海况表给出实际波高参考范围为 1.25～2.5 m，三维海面仿真结果符合参考范围[10]。仿真结果表明，5个采样点处采集得到海面高度数据可以较好地反映理论海浪谱。

表2 统计仿真结果

3.2 波向估计试验

图9为原始海浪谱模型和两种方法得到估计海浪谱模型。图 10为根据海浪谱估计结果得到的波向估计结果，其中峰值处表示主波向的方向，此处能量最大。通过仿真结果可以看出，使用波束形成方法均可估计出海浪的主波向，两种估计方法的主波向均集中在 50°附近。可以看出常规波束形成法估计范围比原始方向分布略大，而 MVDR波束形成分辨率较高。受ADCP采样阵元数限制，在5波束采样条件下常规波束形成分辨率比 MVDR波束形成低。从仿真结果看，坐底式ADCP可以很好地估计海浪方向谱和主波向，且对于有效波高等海浪特性参数的测量较为准确。

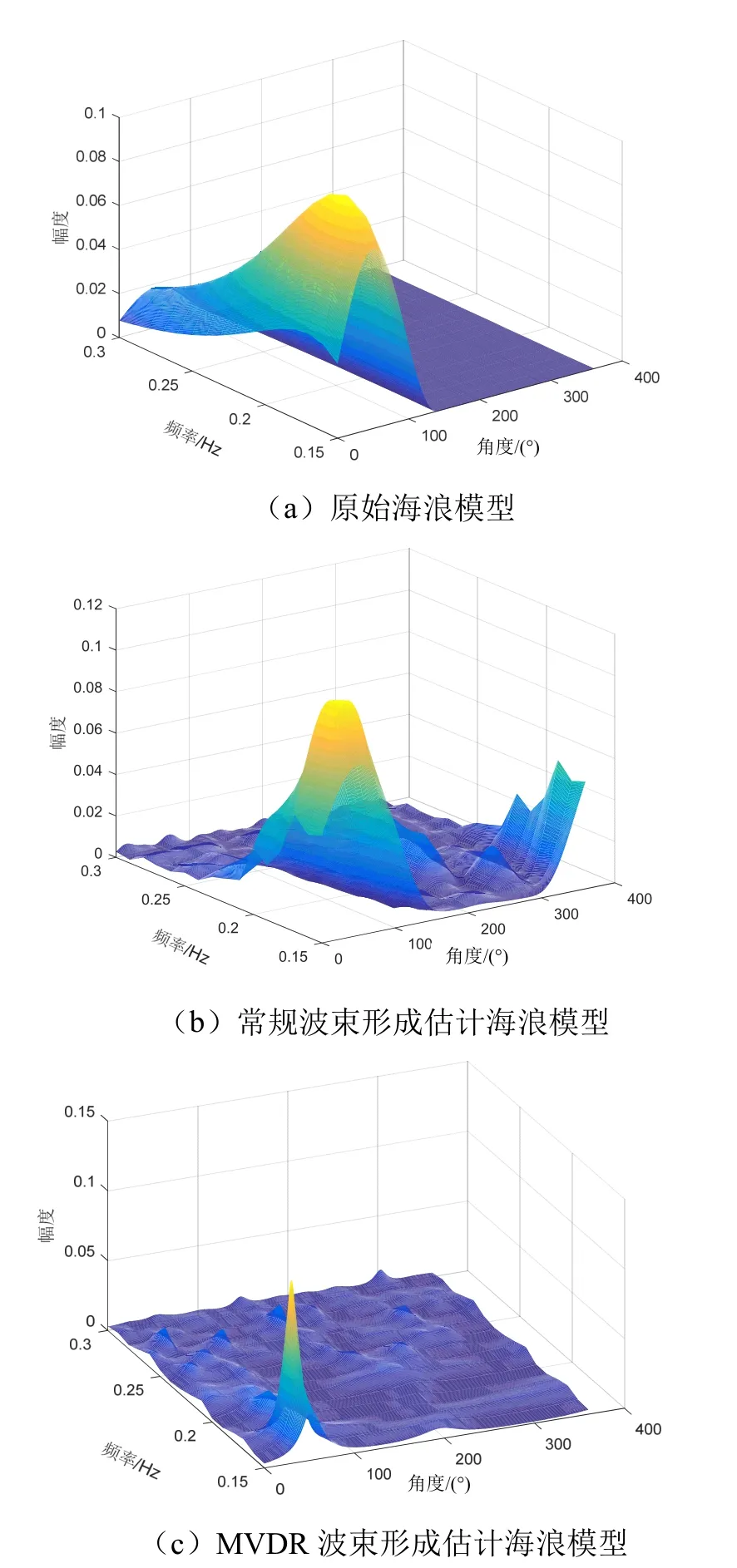
图9 海浪波向谱估计结果

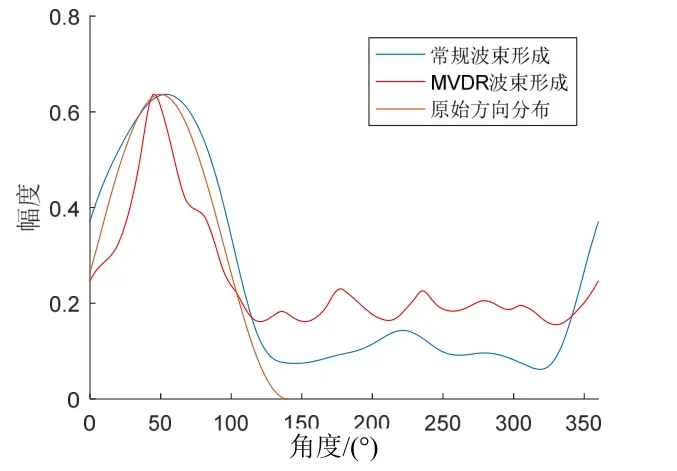
图10 波向估计结果

4 结论

为解决海浪测量中难以获得高准确度波向估计值的难题，本文将波束形成估计达到角的原理应用到海浪波向估计领域。在现有PM海浪谱模型的基础上，建立了三维海浪模型。根据海浪频率与波长关系选择合适仿真频率条件，使坐底式ADCP满足空间采样间距要求。对仿真海浪的海面高度进行测量，利用波束形成法可求得海浪方向谱，根据峰值处角度估计来波方向。建议使用 MVDR进行波向估计。