基于Ginzburg-Landau泛函二值图像复原的快速算法

孙宝宸，李 君，常慧宾

（天津师范大学数学科学学院，天津 300387）

在图像的采集和传输等过程中，噪声污染和信息缺失会导致图像质量降低.图像噪声有多种类型[1]，如高斯噪声、泊松噪声、椒盐噪声等.噪声的多样性使得图像去噪成为一项富有挑战且被广泛关注的研究课题，相关学者提出了多种经典的去噪方法[2-3].

1992年，Rudin等提出的一种以全变差作为正则项的凸ROF模型[2]，可以通过求解其欧拉-拉格朗日方程得到全局最优解，且解是唯一的，之后，一系列快速求解的一阶优化算法被相继提出[4].针对具体噪声的统计性质，可以通过保留全变差正则项改进不同的保真项度量来提高复原图像的质量.ROF模型具有良好的性质，但是全变差项的不可微性使算法设计变得困难，为解决这一问题，一系列光滑化技术被相继提出.文献[5]首次提出使用一类基于双阱势函数（doublewell potential function）的修正模型（简称DP模型）处理图像锐化问题，之后该模型也被应用于图像增强[6]、修复[7-8]和去噪[9]等问题.在文献[10-11]中，基于非局部建模的DP模型首次用于图像分割与数据分类问题.DP模型是逐点可微但非凸的，因此对模型求解具有双重困难：一是直接求解欧拉-拉格朗日方程只能得到局部最优解而无法保证达到全局最优解；二是DP模型的一阶变分是非线性的，很难设计有效的优化算法和梯度流迭代格式.对于全隐梯度流格式，文献[12]证明了若时间步长满足一定的约束条件，则可以保证能量稳定；对于显隐格式，在相场模型的求解中也得到了类似的结论[13].

近年来，一类保能量衰减的显隐迭代格式被应用于相场模型的计算中，如，乘子方法、IEQ格式和SAV格式[13].这类迭代格式通过引入辅助变量改写目标能量泛函，将非线性梯度流方程转化为多变量线性系统，但在实际计算中没有增加需要求解的变量，并能保证改写的等价能量泛函随迭代进行是衰减的.此外，交替方向乘子算法在图像处理的反问题求解中取得了巨大的成功，但目前未见其应用于求解DP模型.

本文首先引入基于Ginzburg-Landau泛函松弛的双阱势模型和2种经典算法，进而通过构造特殊的优化问题，建立了Lie格式与MBO格式的联系，对MBO格式提出了一种从算子分裂优化技术角度的理解方式；然后通过引入辅助变量设计了一类新的算子分裂算法，其子优化问题具有闭形式解；最后通过二值图像复原实验评估各种算法的有效性.

1 双阱势模型和经典算法

1.1 双阱势模型

ROF模型[2-3]的连续形式定义为

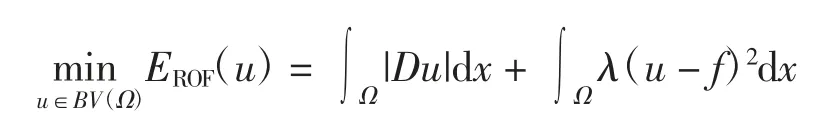
其中：λ为模型参数；Du为u的分布导数；f为污染图像；u为待复原的图像；Ω为二维欧氏空间的一个有界闭集.全变差函数空间为

显然E1ROF（u）关于u是下凸的（若无特殊说明，本文所指的凸性均为下凸性）.对于上述优化问题直接设计迭代格式求解欧拉-拉格朗日方程[4]，即式（1），获得唯一的最优解.

其中：ε为正常数；W（u）为双阱势函数（如W（u）=0.25（u2-1）2，它有2个全局极小值）.文献[16]证明了当ε→0+时，GL（u）会Γ收敛[3]到u的全变差.

基于上述结果将BV（Ω）松弛到H1（Ω）可建立双阱势模型（DP模型）如下

1.2 MBO格式（全隐格式）

文献[17]提出了一种有效的算子分裂格式（记为MBO）.采用MBO格式进行变量更新需要2步迭代：第1步利用向后Euler差分格式求解反应扩散方程ut=Δu；第2步使用1/2水平集进行阈值化.由于DP模型中W（u）项含有2个驻点0和1，所以第2步迭代可表达为

将MBO应用于求解DP模型得到一种修正的MBO格

1.3 凸分裂格式

对于非凸优化问题，若通过能量恒等变换可将非凸的能量泛函转化为凸能量与凹能量之和的形式，则凸分裂格式可视为一种简单有效的数值求解算法，但它通常只有一阶收敛速度.文献[7]将DP模型分解为EDP（u）=E1（u）+E2（u），其中E1（u）=‖Δu‖2+μ‖u（u-1）‖2，为构造凸能量，在不改变目标能量的前提下取E（2u）=λ‖f-u‖2，对E（iu）（i=1、2）设计凸分裂格式.将E（iu）分解为E（iu）=E（i1u）-E（i2u），其中：

文献[7]证明了上述凸分裂格式（convex splitting with 2 mixtures，CS2M）是无条件能量稳定的，即对任意的正整数n，有EDP（un+1）≤EDP（un）.

2 快速迭代求解方法

本节设计一些高效求解DP模型的迭代格式.首先将界面问题的新算法推广到图像复原问题的求解中，然后设计一类基于交替方向乘子方法（alternating direction method of multipliers，ADMM）的新算法.本文算法中均假设u满足Neumann边界条件，即0，其中：Γ为区域Ω的边界，n为单位外法向量.

2.1 相场算法的推广

利用梯度流方程求解能量泛函F的极小化问题，其一般框架为[13]

2.1.1 EQCN格式

文献[21-22]对一类具有特殊结构的目标泛函设计了二阶的显隐差分格式，其核心是通过引进辅助变量将能量泛函的非平方项转化为二次形式，进一步设计能量稳定的时间、空间全离散数值格式，本文考虑其时间半离散格式.定义辅助变量V=u（u-1），将DP模型进行变量分解，则式（3）转化为

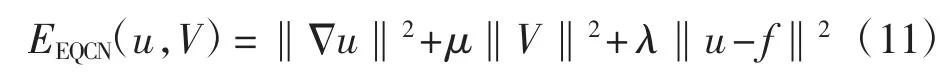
式（11）的梯度流AC方程组为

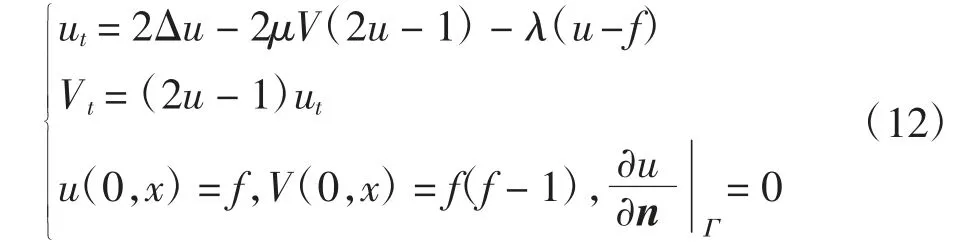
文献[22]通过引入外插和Crank-Nicolson（CN）中心插商构建了迭代格式较为简单且具有二阶收敛速度的EQCN格式.记

利用式（14）进行变量更新，最后使用式（4）进行阈值化.EQCN格式可以保证能量稳定且具有二阶收敛速度[23].

2.1.2 SAVCN格式

文献[13]中提出了具有一阶收敛速度的向前Euler格式、高阶CN和BDF时间半离散格式，本文主要考虑SAVCN格式，其变量更新满足

结合式（15）和式（16）对线性系统进行迭代求解，最后使用式（4）进行阈值化.SAVCN格式可以保证能量稳定且具有二阶收敛速度[13].

2.2 交替方向乘子方法

交替方向乘子方法[24-26]可以处理非凸非光滑的复杂约束优化问题.考虑如下优化问题

上述框架可以自然地推广到无穷维空间上.基于此，本文运用算子分裂技术，通过引入辅助变量将无约束优化问题转化为约束优化问题，设计了2种迭代格式，其子优化问题具有闭形式解.

2.2.1 两变量交替方向乘子算法

引入辅助变量v使得u=v，将W（u）进行算子分裂，原无约束优化问题可修改为约束优化问题：

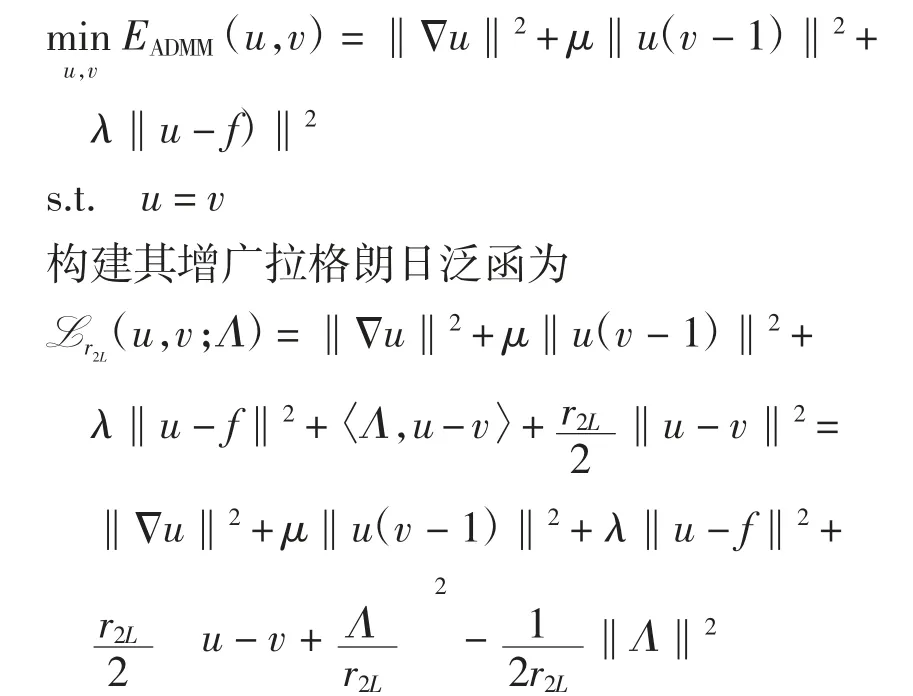
通过交替优化变量和乘子可以得到求解DP问题的新算子分裂格式，其更新框架为

由于其目标泛函是凸可微的，因此可由一阶最优性条件

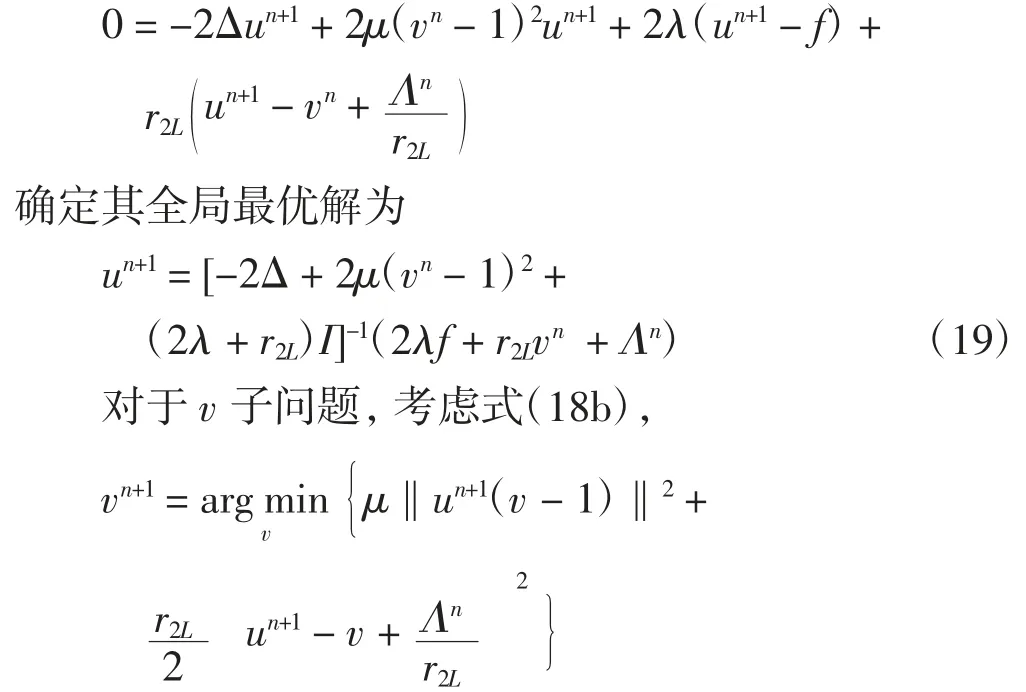
同u子问题的求解过程一致，可得

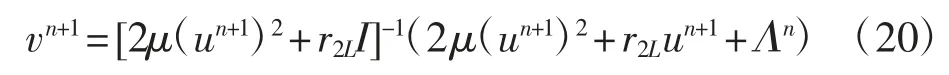
乘子Λ依照式（18c）进行更新.满足终止条件后使用式（4）对u进行阈值化.上述优化算法简记为ADMM2V，其算法流程见表1.

表1 ADMM2V算法流程Tab.1 Algorithm flow of ADMM2V

2.2.2 三变量交替方向乘子算法

类比EQCN格式的解耦思想，本文设计了一种三变量交替方向乘子算法.引入2个辅助变量w和v将W（u）进行算子分裂，无约束优化问题可以转化为约束优化问题：

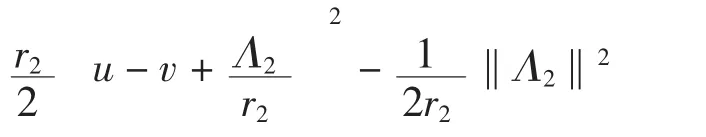
其中：r1和r2为正的增广拉格朗日系数，Λ1和Λ2为乘子.通过交替优化变量和乘子可以得到求解DP问题的新算子分裂格式，其更新框架为

对于乘子Λ1和Λ2按照式（21d）进行更新，满足终止条件后使用式（4）对u进行阈值化.上述优化算法简记为ADMM3V，其算法流程见表2.

表2 ADMM3V算法流程Tab.2 Algorithm flow of ADMM3V

3 数值实验

由于更新格式（12）和（15）考虑的是Neumann边界条件，因此本文对离散图像添加镜像边界，依据文献[27]，对连续的梯度算子离散得Δu（i，j）=（Δux（i，j），Δuy（i，j）），令Nx和Ny分别为离散图像矩阵的行数和列数，其中：

其中：p=（p1，p2），p1=Δux，p2=Δuy.外迭代终止条件设为迭代1 000次或变量u的相对残差小于10-4，即‖un+1-un‖/‖un‖＜10-4.对子问题的线性方程组使用共轭梯度法迭代求解，并设内迭代终止条件为迭代10次或相对误差小于10-10.

3.1 图像去噪

本文主要测试了3种加性噪声（高斯噪声、椒盐噪声和泊松噪声）的复原问题.尽管针对不同种类的噪声，可以设计不同的保真度量以获得更好的去噪效果，但对于不可微的保真项会使基于梯度信息的SAVCN和EQCN格式失效，因此在图像去噪实验中统一采用L2模数作为数据保真项.采用信噪比（SNR）评价去噪效果，

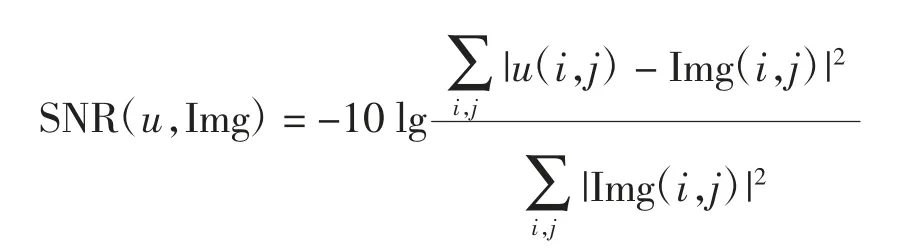
其中：u为去噪后图像，Img为无噪声污染图像.分别采用指纹、条形码和二维码图像（Nx=Ny=256）进行高斯去噪、椒盐去噪和泊松去噪实验，计算mMBO、CS2M、EQCN、SAVCN、ADMM2V和ADMM3V等6种算法的SNR.基于2.2中对mMBO格式的解析，只讨论其他5种算法的数值收敛性和能量衰减性.

对二值化的指纹图像添加服从正态分布N（0，σ2）的高斯噪声，取σ=0.2、0.5和0.8的噪声图像，见图1，各算法复原图像的SNR见表3，6种算法SNR的最大值用黑体标出，下同.

图1 指纹真实图像和高斯噪声图像Fig.1 Real image and Gaussian noisy images of fingerprint

由表3可见，除mMBO外，其他5种算法的SNR基本相同，均高于mMBO.图2给出了变量u的相对误差和总能量EDP（u）的变化曲线.由图2（a）—（c）可见，5种算法的收敛速度没有显著差异.由图2（d）—（f）可见，各算法都保证了能量衰减性，但能量衰减的速度不一致.当σ=0.2时，EQCN和SAVCN能量下降得最快；当σ=0.5时，各算法的能量降速基本一致，当σ=0.8时，ADMM能量下降得最快.

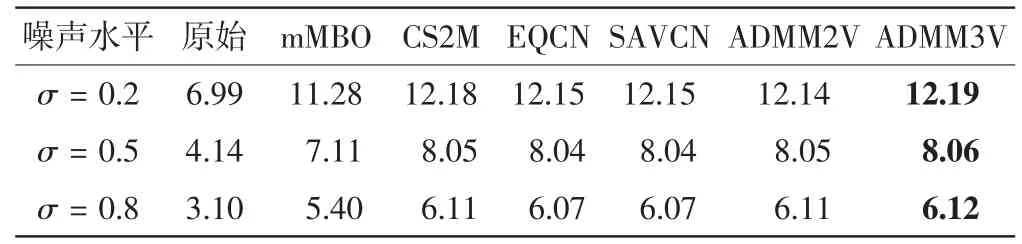
表3 高斯去噪实验的SNRTab.3 SNR of image denoising experiments of Gaussian noisydB

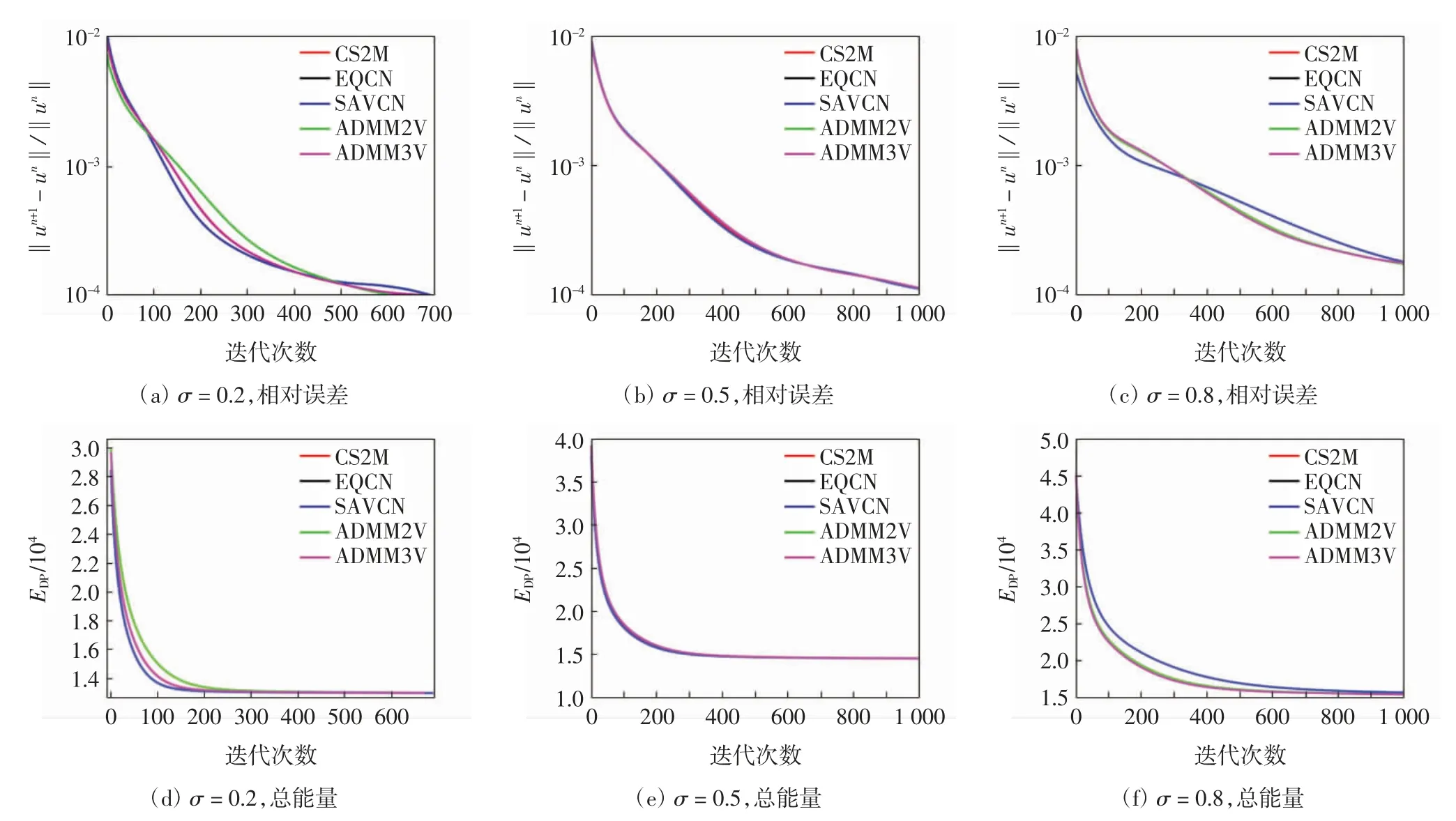
图2 高斯去噪实验相对误差与总能量的变化情况Fig.2 Changes of relative residuals and total energy in Gaussian denoising experiment

对二值化的条形码图像添加强度为ρ的椒盐噪声，取ρ=0.05、0.10和0.20的噪声图像，见图3，各算法复原图像的SNR见表4.由表4可见，除mMBO外，其他5种算法的SNR基本相同，均高于mMBO.图4给出了变量u的相对误差和总能量EDP（u）的变化曲线.由图4（a）—（c）可见，5种算法的收敛速度没有显著差异.由图4（d）—（f）可见，各算法都保证了能量衰减性，对于ρ=0.05、0.10和0.20，均为ADMM能量下降得最快.

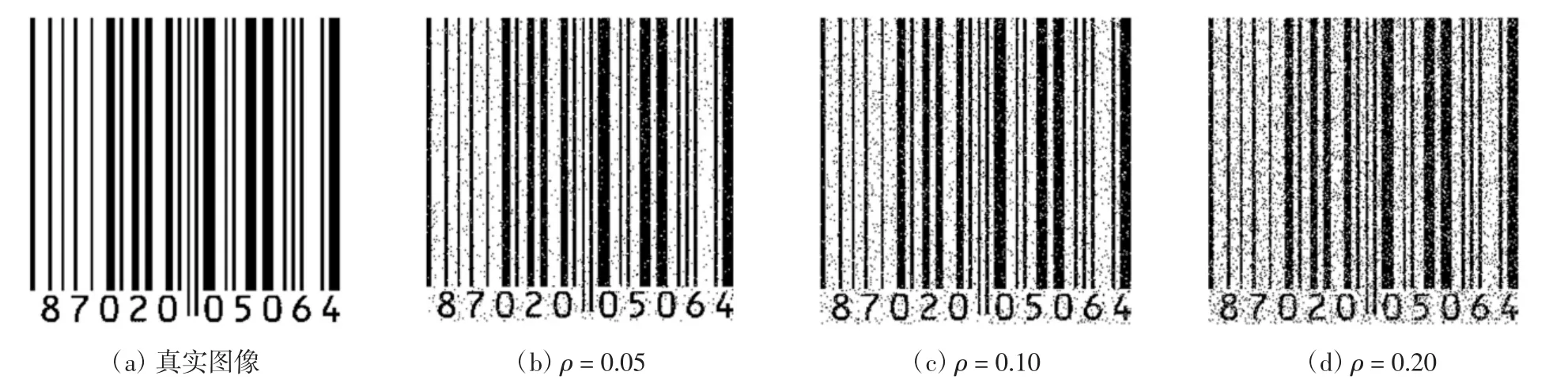
图3 条形码真实图像与椒盐噪声图像Fig.3 Real image and salt and pepper noisy images of barcode

表4 椒盐去噪实验的SNRTab.4 SNR of image denoising experiments of salt and pepper noisy dB

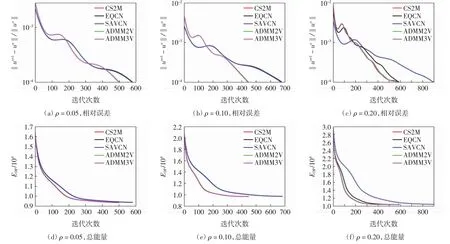
图4 椒盐去噪实验相对误差与总能量的变化情况Fig.4 Changes of relative residuals and total energy in salt and pepper denoising experiment

对二值化的二维码图像逐点添加泊松噪声，服从Poisson（ηf（i，j））/η分布，取η=4、8和16的噪声图像，见图5，各算法复原图像的SNR见表5.由表5可见，除mMBO外，其他5种算法的SNR均较高，ADMM2V的SNR最高.图6给出了变量u的相对误差和总能量EDP（u）的变化曲线.由图6（a）—（c）可见，5种算法的收敛速度没有显著差异，但在优先保证EDP（u）充分下降的前提下，2种ADMM算法的收敛速度较快.由图6（d）—（f）可见，各算法都保证了能量衰减性，对于η=4、8和16，均为ADMM能量下降得最快.

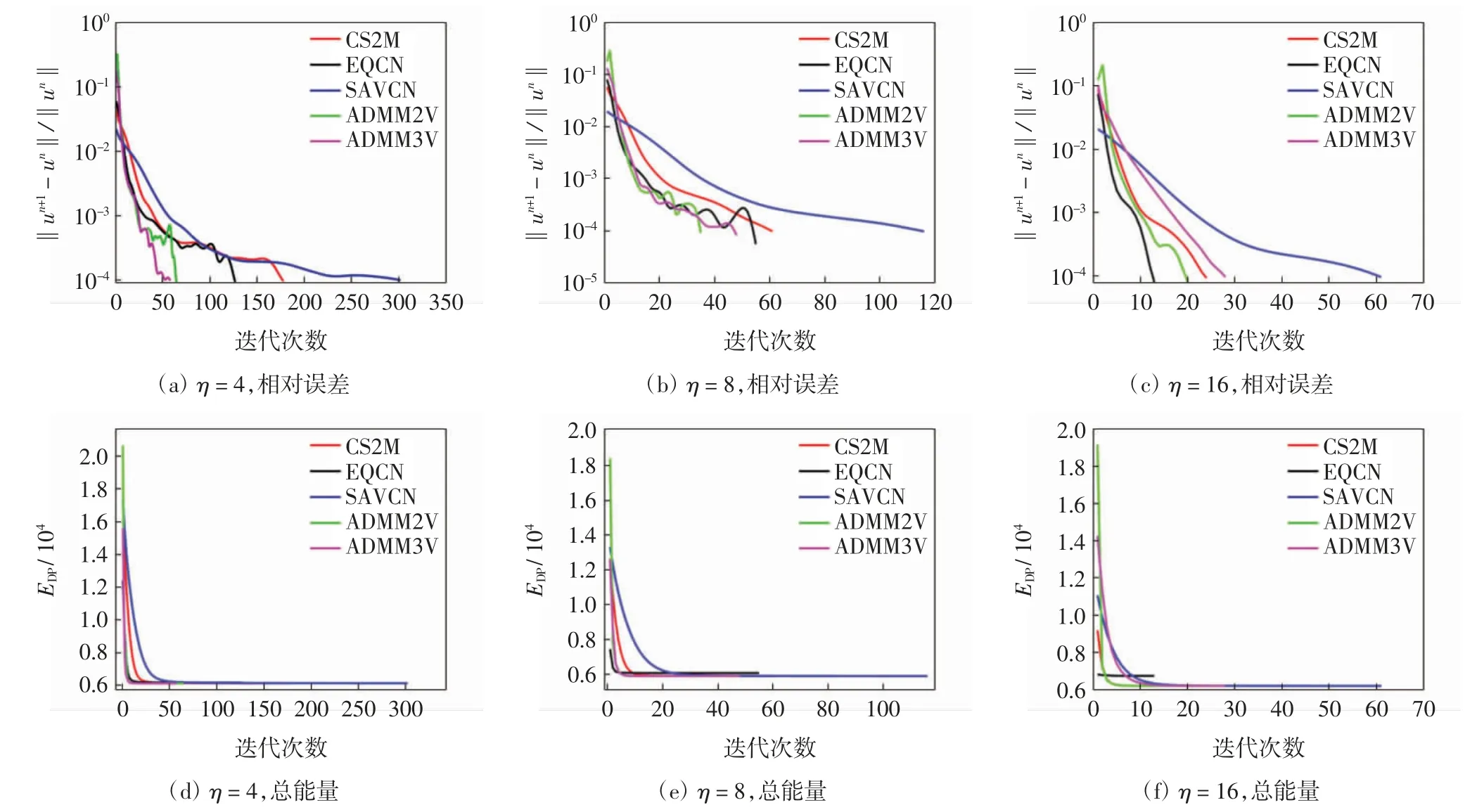
图6 泊松去噪实验相对误差与总能量的变化情况Fig.6 Changes of relative residuals and total energy in Poisson denoising experiment

表5 泊松去噪实验的SNRTab.5 SNR of image denoising experiments of Poisson noisy dB

图5 二维码真实图像与泊松噪声图像Fig.5 Real image and Poisson noisy images of QR code

3.2 图像修复

对于图像修复问题需要将DP模型中的λ∈R+修改为

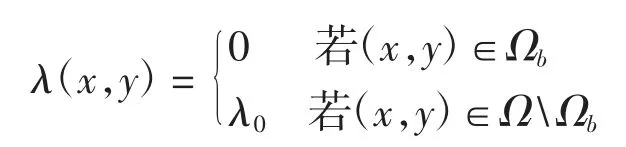
其中：Ωb为待修复部分；λ0为一个正常数.考虑简单结构和复杂结构2类图像的修复问题，以修复后图像与真实图像的均方误差（MSE）评价修复效果，

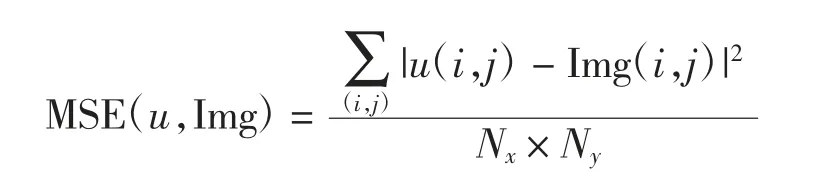
在简单结构图像修复实验中，对二值化的矩形拼接图（Nx=Ny=128）设置不同比例的区域信息缺失，缺失比例分别设为30%、50%和70%，见图7，各算法修复图像的MSE见表6，6种算法MSE的最小值用黑体标出，下同.

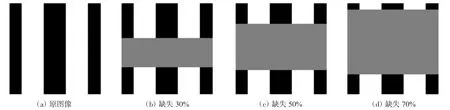
图7 矩形拼接图的真实图像与待修复图像Fig.7 Real image of rectangular and images to be inpainting

由表6可见，SAVCN算法的修复效果最优.图8给出了变量u的相对误差和总能量EDP（u）的变化曲线.由图8（a）—（c）可见，在迭代初期，2种ADMM算法收敛较快，而随着迭代次数增多，SAVCN格式的收敛速度超过其他算法.由图8（d）—（f）可见，各算法都保证了能量衰减性，但CS2M的总能量随迭代次数增多先上升后下降，最终达到稳态.

表6 矩形拼接图像修复实验数值结果（MSE）Tab.6 Numerical results（MSE）of rectangular image inpainting experiments

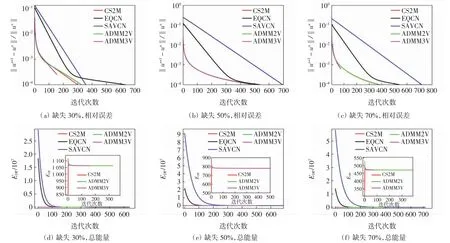
图8 矩形拼接图像修复数值实验相对误差与总能量的变化情况Fig.8 Changes of relative residuals and total energy in image inpainting numerical experiments for rectangular

在复杂结构图像修复实验中，对条形码和二维码图像（Nx=Ny=256）分别设置不同的局部区域信息缺失，见图9，各算法修复图像的MSE见表7.

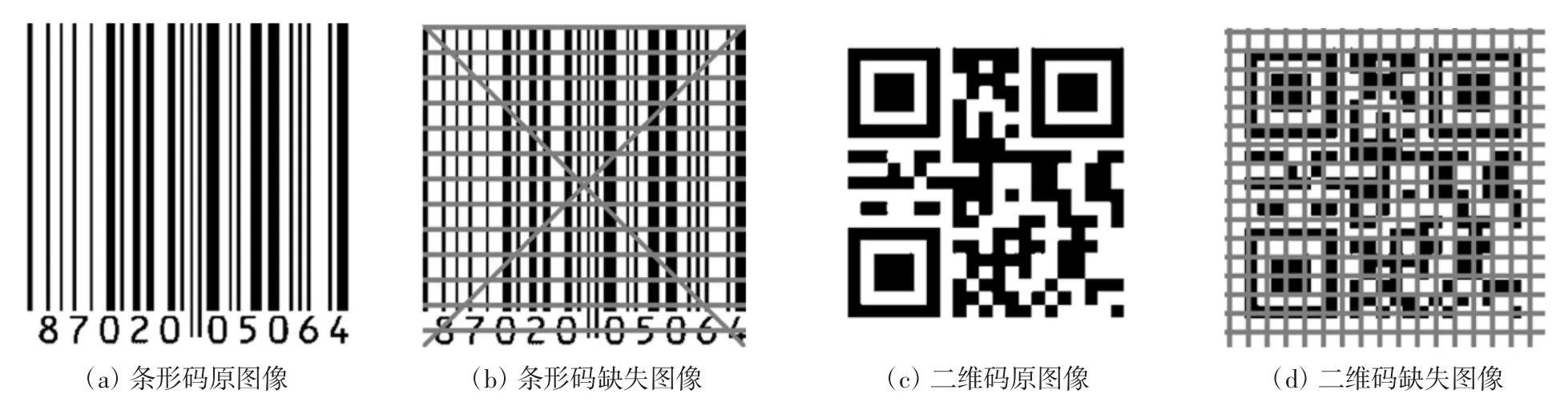
图9 条形码和二维码的真实图像与待修复图像Fig.9 Real images of barcode and QR code and images to be inpainting

由表7可见，SAVCN算法的修复效果最优.图10给出了变量u的相对误差和总能量EDP（u）的变化曲线.由图10（a）和（b）可见，对于条形码图像，CS2M收敛最快，对于二维码图像，2种ADMM算法和CS2M收敛速度基本一致，高于其他算法.由图10（c）和（d）可见，各算法均可保证目标总能量最终达到稳态.

图10 条形码和二维码图像修复数值实验相对误差与总能量变化情况Fig.10 Changes of relative residuals and total energy in image inpainting numerical experiments for barcode and QR code

表7 条形码和二维码图像修复实验数值结果（MSE）Tab.7 Numerical results（MSE）of barcode and QR code images inpainting experiments

对于以上图像去噪和修复实验，图11给出了ADMM和SAVCN算法中超参数对图像复原效果的影响.由图11（a）可见，ADMM2V的参数r2L对最终的结果数值影响是敏感的.由图11（b）和（c）可见，SAVCN的参数τ和ADMM3V的参数r1、r2对最终的结果数值影响均不敏感.

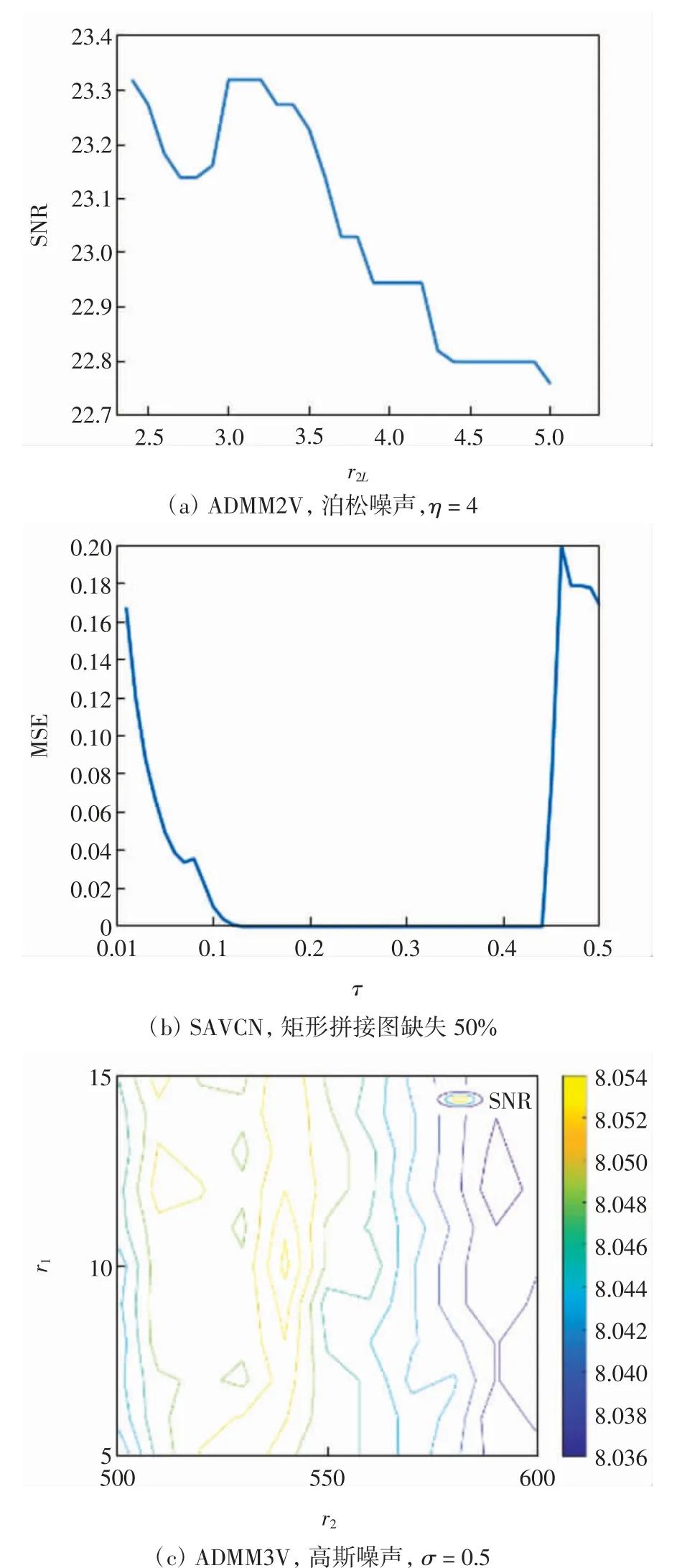
图11 算法参数对图像复原结果的影响Fig.11 Influences of algorithm parameters on image restoration results

4 结论

本文利用DP模型处理二值图像复原问题，主要考虑了三种成熟的半隐迭代格式和两种新的ADMM算法.数值算例的结果表明，本文所提出的ADMM方法去噪实验中可以恢复到信噪比更高的结果且保持能量稳定，在修复实验中，SAVCN格式最终修复所得结果更好，但其收敛速度较慢

鉴于ADMM算法在图像去噪实验中表现出稳定的优势，因此在后续的研究中，将对ADMM算法的收敛性进行分析.除此之外，考虑到SAVCN格式在图像修复中表现良好，从而将在后续研究中设计更为稳定的能量衰减迭代格式.