分担值与亚纯函数的正规性

张海侠

(许昌学院 数理学院,河南 许昌 461000)

亚纯函数的正规族理论是复分析的一个重要组成部分,也是研究复分析问题的一个主要工具.上世纪初广泛应用在复动力系统中.P.Montel引进了正规族的概念并且给出了一个判定函数族正规的基本定则,即Montel正规定则，1931年F.Marty在Montel定则的基础上建立了另一个著名Marty正规定则.后来,陈怀惠和顾永兴[1]对Marty定则进行了推广与改进.W.Schwick[2]把亚纯函数正规族与分担值结合起来考虑亚纯函数正规族理论问题,研究发现分担值与正规定则之间的联系，随后,FANG M L等[3],PANG X C等[4],FANG M L等[5]把双向分担值与导数结合起来考虑亚纯函数的正规性问题并取得了一系列的研究成果，把单项分担值与导数结合起来考虑亚纯函数的正规性问题，得到与导数有单向分担值的亚纯函数族的正规定则.

1 预备知识

设f(z)和g(z)是区域D内的两个亚纯函数,a是一个复数,若f(z)-a与g(z)-a在D内有相同的零点,则称f(z)与g(z)在区域D内分担a,或称IM分担a.记为

f(z)=a⟺g(z)=a.

如果f(z)-a的零点为zn(n=1,2,…),且zn(n=1,2,…)也是g(z)的零点(不计重数),则记为

f(z)=a⟹g(z)=a.

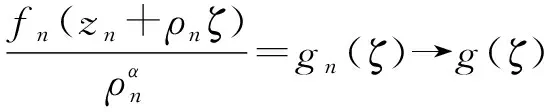
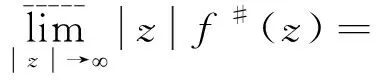
引理4[7](Hurwitz定理) 设函数序列{fn(z)}在区域D内解析,并且在D内闭一致收敛到一个不恒为零的函数,γ是D内可求长的闭曲线,其内部属于D,且不经过f(z)的零点,则存在正整数N,使得当n≥N时,在γ内部,fn(z)和f(z)的零点个数是相同的.

引理5[8]设F是区域D上的亚纯函数,且h(z)为D上的亚纯函数,k∈N若对于任意的z∈D,有h(z)≠0，假设对任意的f∈F，满足f(z)=0⟺f′(z)=h(z)⟹|f″(z)|≤c(c为常数)，则F在D上正规.

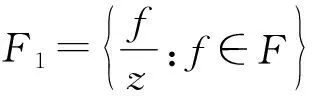
引理7[10]若F满足引理5的条件,则F在D-0上正规.

2 亚纯函数的正规性

2005年,张国明、孙伟、庞学诚给出了下面结论：

命题[8]设F是平面上区域D上的亚纯函数族,如果对于任意的f∈F,都有

f(z)=0 ⟺f′(z)=z⟹ |f″(z)|≤c,

其中c为常数且f(0)≠0，则F在D上正规.

该结论是把双向分担值与导数结合起来考虑亚纯函数的正规性问题，若把单项分担值与导数结合起来考虑亚纯函数的正规性问题，将得到一个新的有价值的新结论，即是与导数有单向分担值的亚纯函数族的正规定则.

定理1 设F是区域D上的一族亚纯函数,若对于任意的f∈F,有

(1)f(z)=0⟹f′(z)=z⟹f″(z)=0.

(2)若f(0)≠0，则F在D上正规.(不再限制零点的级).

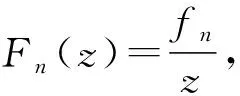
在复平面C的意紧子集上依球面距离内闭一致成立，其中，g为非常数的整函数g#(ζ)≤g#(0)=2.

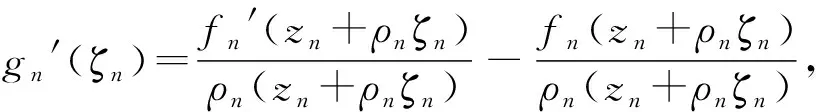
因此，g(ζ)=0⟹g′(ζ)=1.

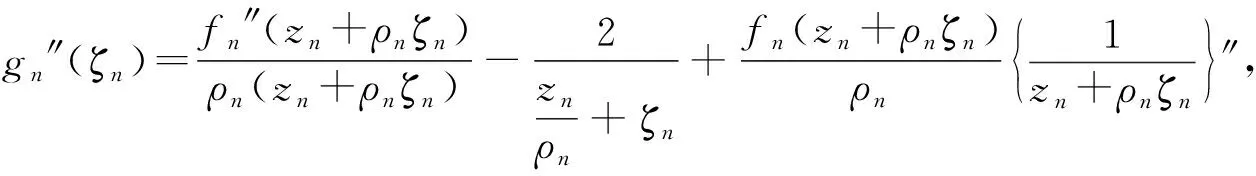
g(ζ)=0 ⟹g′(ζ)=1 ⟹g″(ζ)=0，

由引理2,引理3知g(ζ)=ζ-b,所以g#(ζ)≤1与g#(0)=2矛盾，从而结论成立.

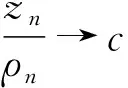
类似方法(ⅰ)，可得出G=0 ⟹G′=z⟹G″=0.

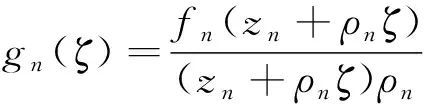
(2)若G为多项式，结合G′(ζ)=ζ为非常数,则G的次数k至少为2.

若G(0)≠0,由G(ζ)=0 ⟹G′(ζ)=ζ,所以G的零点均为单零点.

又因G的次数为k,知方程G(ζ)=0有k个不同的解,而方程G′(ζ)=ζ有k-1个不同的解,与G(ζ)=0 ⟹G′(ζ)=ζ矛盾，所以，G(0)=0且G′(0)=0,ζ=0为G(ζ)的至少二重零点.

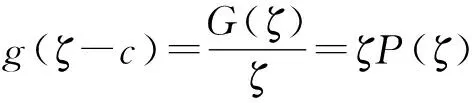
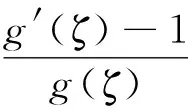
由此可见，g#(0)≤1与g#(0)=2矛盾.则F1在z=0处正规，从而定理结论(2)成立.

通过上面的讨论可以看到，在利用亚纯函数正规族的有关理论、亚纯函数正规族及其导数与分担值结合考虑的前提下,得出了涉及导数与单向分担值的亚纯函数的正规性定理,把亚纯函数正规性的范围做了一些推广,得到了关于亚纯函数正规性的重要理论结果.