沥青复合模量与温度关联研究及数学模型的建立

张小英，徐传杰，张 强

（1.中国石油大学 重质油加工国家重点实验室，山东 青岛 266580；2.山东石大科技集团有限公司，山东 东营 257062）

沥青材料是兼具黏性流动和弹性形变特点的黏弹性材料[1]，其显著的力学特征随加载方式、载荷大小、施加荷载的时间和温度的变化而变化。20世纪末美国战略公路研究(SHRP)计划开发的动态剪切流变仪实验是研究沥青黏弹性的有效技术。该实验得到两个基础的技术指标，一个是表征变形总阻力的复合模量G*，另一个是反映应变滞后应力速度的指标，即相位角δ。G*由存储模量G´(G*cosδ)和损耗模量G〃(G*sinδ)两部分组成，是一定应变下材料内部产生阻力大小的量度。δ是表征损耗模量和存储模量的指标。线性黏弹性区间的剪切应力和剪切应变之间的关系只受温度和时间影响，与剪切应力或剪切应变的大小无关[2]。

美国基于动态剪切流变仪实验方法和线性黏弹性区间黏弹响应特性开发的路用沥青PG分级体系[3]（Performance Grading System）提出了在高、中温与路面使用环境相关的流变特性量化指标确定沥青的等级。用原样沥青的车辙因子（G*/sinδ）评价未拌和之前沥青的高温抗车辙性能；用旋转薄膜烘箱后(RTFOT)的G*/sinδ评价沥青材料高温拌和、摊铺碾压后沥青材料高温抗车辙性能；用旋转薄膜烘箱后再经历压力老化容器实验(PAV)的沥青材料的疲劳因子G*sinδ评价沥青在路面上使用10~15 a后沥青材料的中温抗疲劳性能。通过弯曲梁流变仪测量PAV后样品得到的弯曲蠕变劲度S、对数蠕变劲度斜率m及直接拉伸实验得到的破坏应力和破坏应变，共同为低温等级提供分级指标。除了135℃黏度和闪点外[4]，PG分级体系与长期使用针入度分级体系[5]和黏度分级体系[6]完全不同。3个分级体系各有优缺点且相互独立[4]，分别在世界各国独立使用。但是这种应用现状也造成了各国在路面建设中的经验无法交融和共享[7]。

要明确3个体系的发展趋势,就必须理解3个体系中各指标之间的特性以及不同评价体系之间的关系。3个体系中沥青的评价指标都是在常压下进行评价和研究，因此温度成为与各指标密切相关的基础变量。而固定频率下在线性黏弹性区间采用恒应力或恒应变的方式固定了加载时间、载荷大小、加载频率、加载方式等对流变性质影响，这为揭示复合模量的温度特性提供了条件，同时也为3个分级体系间流变性质的关联创造了条件。

关于复合模量与温度的关系，研究人员针对沥青或改性沥青，通过复合模量的双对数与绝对温度的 对 数[8⁃9]或 与 摄 氏 温 度[10⁃11]线 性 关 系 的 斜 率 来 判 断沥青材料的温度敏感性。还有一些研究采用存储模量和损耗模量的对数[12]、双对数[13]与绝对温度的对数的斜率研究改性沥青的温度敏感性，这些研究证明复合模量与温度之间具有非常高的关联性。

以上关联都具有相似的表达方式，但未对这些线性关系的优劣进行对比，未找出适合表征复合模量和温度的更优关联，未在复合模量与温度之间建立数学模型。本研究以解决这些问题为目标进行研究，力求充分理解复合模量的温度特性，并为3个评价体系之间的关联寻求技术支撑。

1 研究内容及实验方法

采用两种不同原油生产的10个不同针入度6个牌号的原样沥青及其RTFOT后和PAV后沥青共30个品种为研究对象。测定其不同温度下的复合模量，并将复合模量的双对数与不同温度的表达式进行线性拟合，对比不同拟合关系的优劣，找出复合模量与温度的最佳拟合关系，并建立数学模型。用第三种原油得到的3个不同针入度不同老化阶段沥青复合模量实测数据与预测数据进行对比，验证数学模型的准确性、可行性。

复合模量的测定方法采用SH/T 0777-2003[14]或ASTM D7175-08[15]，在线性黏弹性区间进行研究。实验条件：应变式控制模式，应变值γ=12%，频率=10 rad/s，对原样沥青和RTFOT后沥青，采用平行板直径25 mm，板间隙1 mm；PAV后沥青，采用平行板直径8 mm，板间隙2 mm。

10个原样沥青产品的性质见表1。由表1可以看出，10个沥青都满足相应牌号的重交通道路沥青产品技术指标的要求。

表1 原样沥青产品性质Table 1 Pr oper ties of or iginal asphalts

续表1

2 温度与复合模量的关联研究

线性相关性是具有直线关系的两个变量间相关密切程度和相关方向的指标。在线性关系中相关系数r的绝对值越接近1，两个变量之间的线性关系越高。当r的绝对值等于1时，两个变量呈完全线性关系。

3个不同老化阶段复合模量的双对数与摄氏温度、绝对温度、摄氏温度的对数和绝对温度的对数之间线性拟合方程中的斜率K、截距B和相关系数r见表2-5。由表2-5可以看出，对于原样沥青、RTFOT后沥青、PAV后沥青，虽然拟合关系的斜率或截距数据不同，但是其复合模量双对数都随着摄氏温度、绝对温度、摄氏温度对数和绝对温度对数的增加而降低。4个线性关系均为高度负相关，相关系数的绝对值均高于0.993 0，这与文献[8-13]研究结果是一致的。

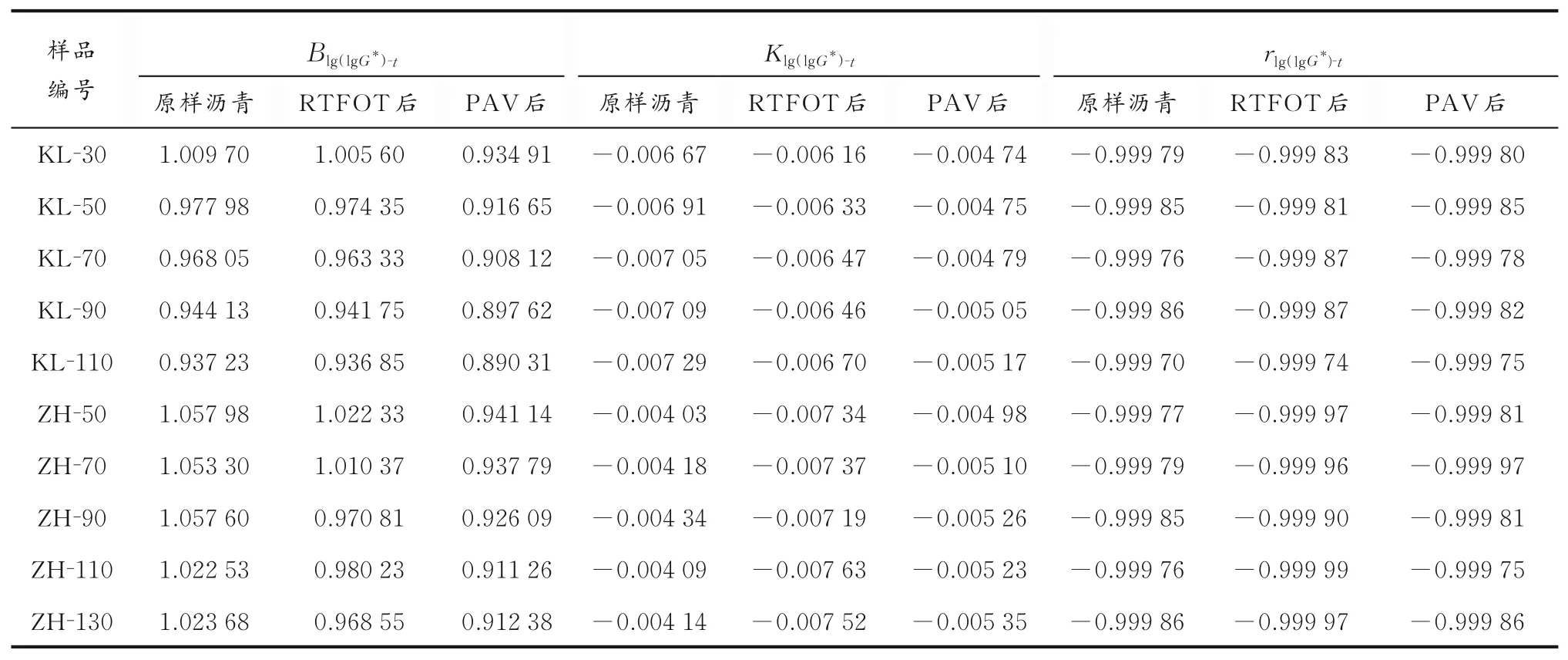
表2 复合模量双对数与摄氏温度拟合参数Table 2 Parameters of the linear r elationship between lg（lg G*）and t

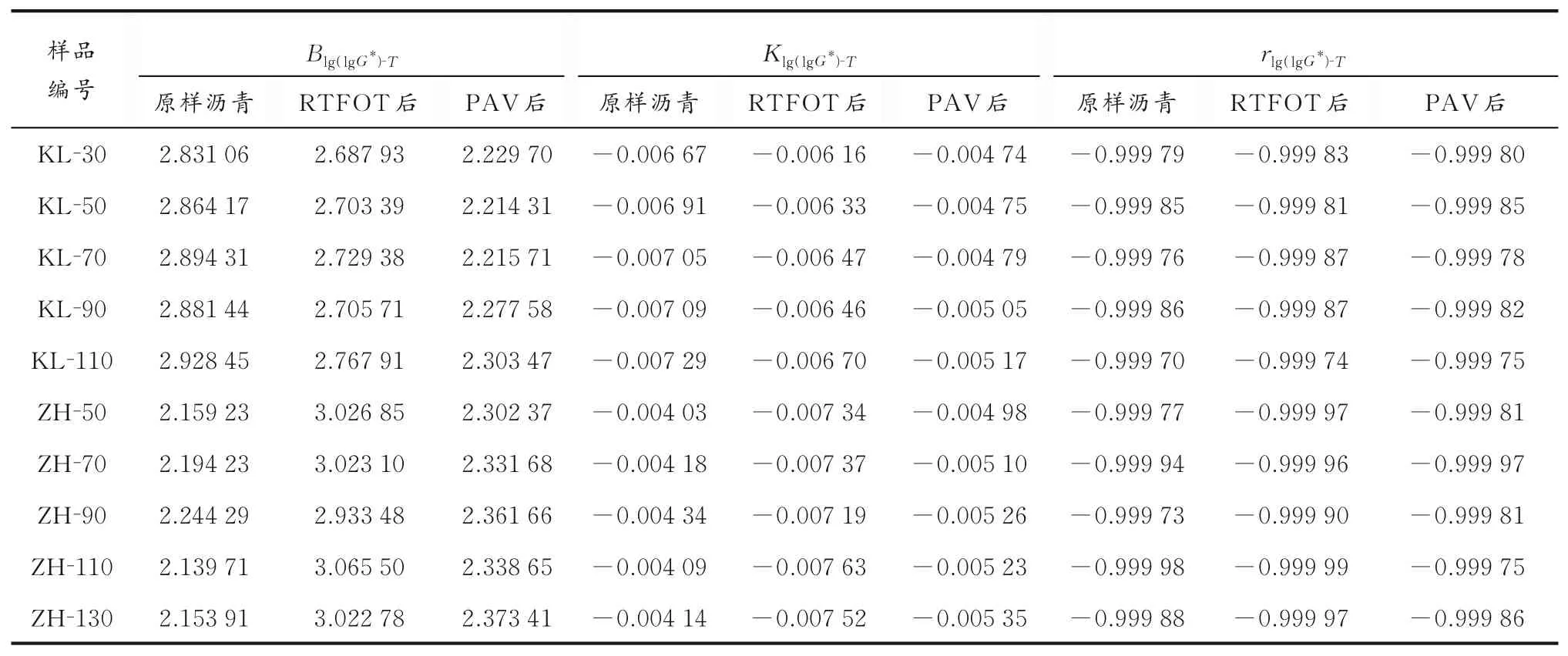
表3 复合模量双对数与绝对温度拟合参数Table 3 Parameter s of the r elationship between lg（lg G*）and T

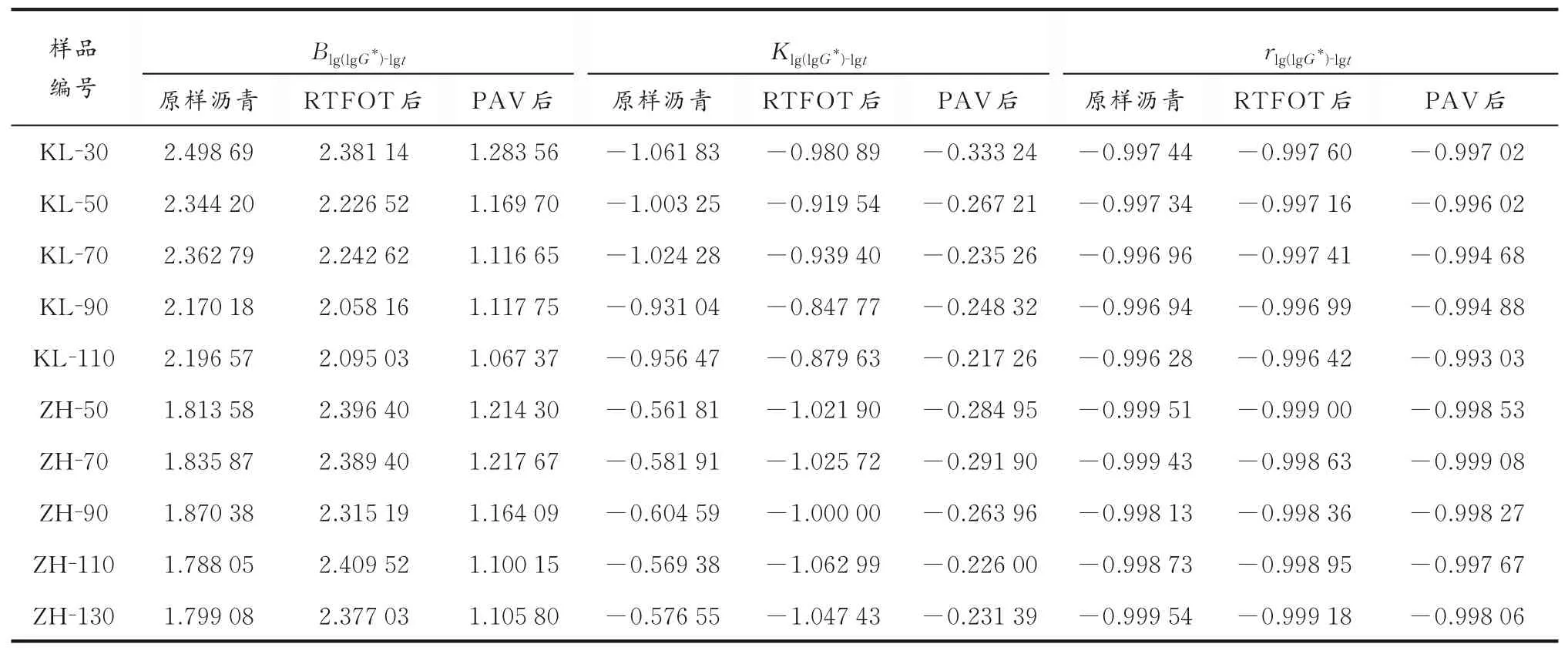
表4 复合模量双对数与摄氏温度的对数拟合参数Table 4 Equation and parameter of the relationship between lg（lg G*）and lg t

表5 复合模量双对数与绝对温度的对数拟合参数Table 5 Parameters of the relationship between lg（lg G*）and lg T

对于KL原油生产的沥青，4种拟合关系的斜率K的绝对值和截距B均随着老化深度的增加而降低。而对于ZH原油生产的沥青，随着老化深度的增加，当复合模量双对数与摄氏温度和绝对温度进行关联时，B值降低，K值的绝对值顺序为：RTFOT后>PAV后>原样沥青；当与摄氏温度对数进行关联时，随着老化深度的增加，B值和K值的绝对值高低顺序均为：RTFOT后>原样沥青>PAV后；当与绝对温度对数进行关联时，ZH生产的沥青B值和K值的绝对值高低顺序为：RTFOT后>PAV后>原样沥青。

这些规律说明虽然复合模量的双对数与4个温度表达式均高度线性相关，且都随着温度或温度的对数的增加模量双对数降低，但是随着老化深度的变化，K值和B值的升降规律不仅会随着原油的不同而不同，也会随着温度表达方式的不同而不同。如果用复合模量的双对数与不同温度表达方式进行关联的斜率代表温度敏感性的话，用KL原油生产的沥青温度敏感性的排序都是随着老化深度的增加，温度敏感性降低。但对ZH原油生产的沥青，4个拟合关系随着老化深度的不同，K值增加或降低的趋势是不同的，这说明采用不同的温度表达式得到的温度敏感性的排序是不同的。因为文献[8-13]中复合模量的双对数与摄氏温度或绝对温度的对数进行线性拟合时均采用一种温度表达方式，没有多种温度拟合关系的对比，所以本研究首次发现采用不同温度表达式的斜率表达敏感性其排序是不同的。

3 线性拟合关系的优劣对比

判断温度敏感性高低、复合模量与温度拟合关系准确性,需对拟合关系进行对比研究。

从表2-5可以看出，30个沥青复合模量双对数与摄氏温度和绝对温度的相关系数均分别相等且均大于0.999 70；而与绝对温度对数的相关系数均大于0.999 38；与摄氏温度对数的相关系数均大于0.993 03。这说明4个拟合关系线性相关性都非常高，这证实了在线性黏弹性区间复合模量与温度有非常密切的关联性。从相关系数的对比还可以看出，30个沥青每一组复合模量和温度数据，其相关系数绝 对 值 高 低 顺序均为：rlg(lgG*)⁃t=rlg(lgG*)⁃T>rlg(lgG*)⁃lgT>rlg(lgG*)⁃lgt。rlg(lgG*)⁃lgt的相关系数最小,只有3个相关系数大于0.999 00。rlg(lgG*)⁃lgT的相关系数虽然居于第三位，但 其 与rlg(lgG*）⁃T、rlg（lgG*）⁃t的 相 关 系 数 相 比，相 关 系数都只在小数点后的第4位或第5位数据发生变化。在拟合方程斜率和截距对比的过程中发现，除了复合模量和摄氏温度拟合关系外，其余3个拟合关系的斜率和截距之间也存在一定的关系。

为了避免数据的偶然误差影响相关性优劣的判断，同时明确4个线性关系相关性的优劣，将斜率和截距分别进行线性拟合，拟合参数见表6。

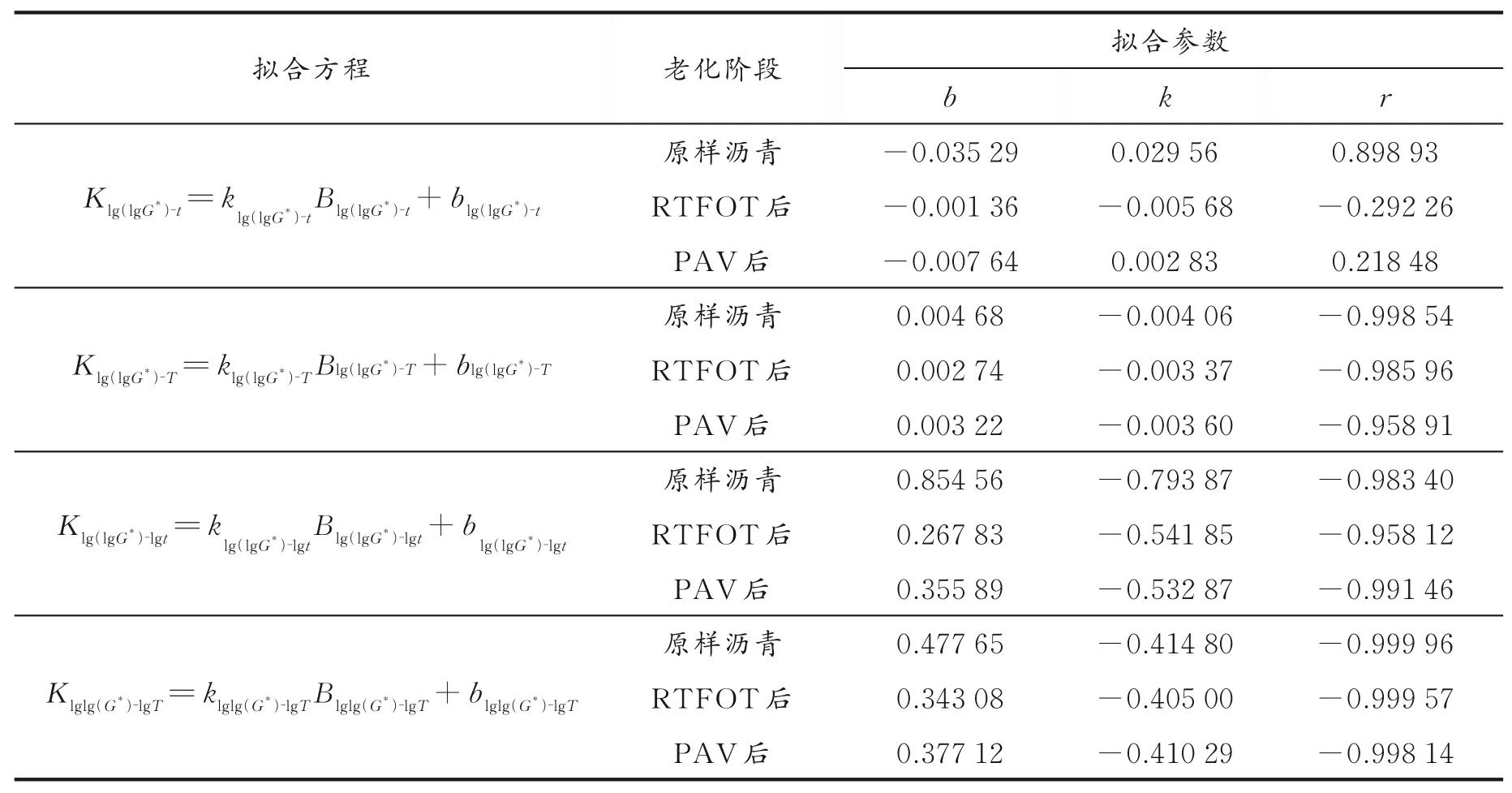
表6 不同老化阶段的温度表达式中斜率和截距之间线性拟合方程及参数Table 6 Equation and par ameter of the r elationship between slope and intercept in temperatur e expr essions of different stages

通过表6的对比发现：r原样沥青>rRTFOT>rPAV。当不同温度表达式间进行对比时，复合模量双对数与摄氏温度拟合关系的斜率和截距的相关系数绝对值除了原样沥青接近0.900 00，RTFOT后和PAV后的沥青均低于0.300 00；与绝对温度拟合方程的斜率和截距的相关系数绝对值在0.958 91~0.998 54；与摄氏温度的对数的斜率和截距的相关系数绝对值在0.958 12~0.991 46；而与绝对温度的对数的斜率和截距的相关系数的绝对值在

0.998 14~0.999 96。

综上，除复合模量的双对数与摄氏温度之间拟合关系的斜率和截距外，其他3种线性拟合关系的斜率和截距之间也具有很高的相关性，其中复合模量的对数与绝对温度的对数的斜率和截距之间的相关性最高。

由复合模量的双对数与绝对温度的对数线性关系的相关系数的排序，同时结合其拟合关系的斜率和截距之间存在几乎完全线性关系，明确了复合模量双对数与绝对温度的对数之间的关联最适合表征复合模量与温度之间的关联。因为用复合模量双对数与绝对温度对数之间的斜率判断温度敏感性具有很高的准确性。同时通过斜率和截距之间 的 一 一 对 应 关 系 也 可 以 判 断：截 距Blg（lgG*）⁃lgT也 可用 于 决定 温 度 敏感 性，其排 序 应 与Klg（lgG*）⁃lgT的 温 度敏感性排序完全相同。

4 数学模型的建立

根据表6可知，复合模量双对数与绝对温度对数的拟合方程为：

式中，G*为温度T下的复合模量，Pa⋅s；T为实验温度，K；Klg（lgG*）⁃lgT和Blg（lgG*）⁃lgT为 常 数，Blg（lgG*）⁃lgT的 物 理意义为当绝对温度等于1 K时复合模量的双对数。

从 表6可 以 看 出，Klg（lgG*）⁃lgT和Blg（lgG*）⁃lgT拟 合 方程为：

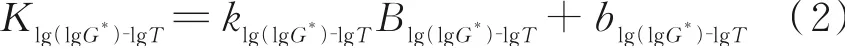
式中，k和b分别为Klg（lgG*）⁃lgT与Blg（lgG*）⁃lgT线性拟合关系的斜率和截距，为常数。

将式（2）代入式（1）中得到：

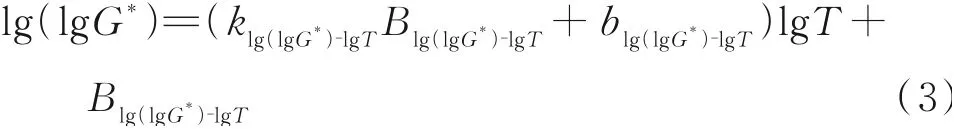
将不同老化阶段的斜率和截距拟合关系得到的klg（lgG*）⁃lgT和blg（lgG*）⁃lgT分 别 代 入 式（3）中就得到了 适合不同老化阶段的复合模量与温度的方程，即：

因 为Klg（lgG*）⁃lgT和Blg（lgG*）⁃lgT几 乎 完 全 线 性 相 关，式（4）-（6）中的Blg（lgG*）⁃lgT也可以用Klg（lgG*）⁃lgT关系取代。由此可以得出复合模量双对数与绝对温度对数和Klg（lgG*）⁃lgT或Blg（lgG*）⁃lgT密切相关。

建立的复合模量与温度之间的数学模型，需满足于所有的沥青，而且有相对单一的表达式。研究中3个不同老化阶段的30个沥青分别满足式（4）-（6）。这说明式（4）-（6）具备复合模量和温度之间的数学模型的特点。数学模型成立的条件与PG分级中复合模量的测定条件相同。

对于式（4）-（6），只需在相同老化阶段线性黏弹性区间测定一个温度下的复合模量，就可以得出常数Blg（lgG*）⁃lgT，通过式（4）-（6），可以计算出对应老化阶段线性黏弹性区间其他温度下的复合模量。

5 数学模型的验证

为了验证数学模型的准确性，研究采用不同于上述研究中的第三种原油生产的LH⁃70、LH⁃90、LH⁃110沥青分别测定原样沥青、RTFOT后沥青和PAV后沥青的复合模量，实测结果和采用式（4）-（6）预测的结果见表7。计算Blg（lgG*）⁃lgT采用的温度为测试温度范围中间值的温度。

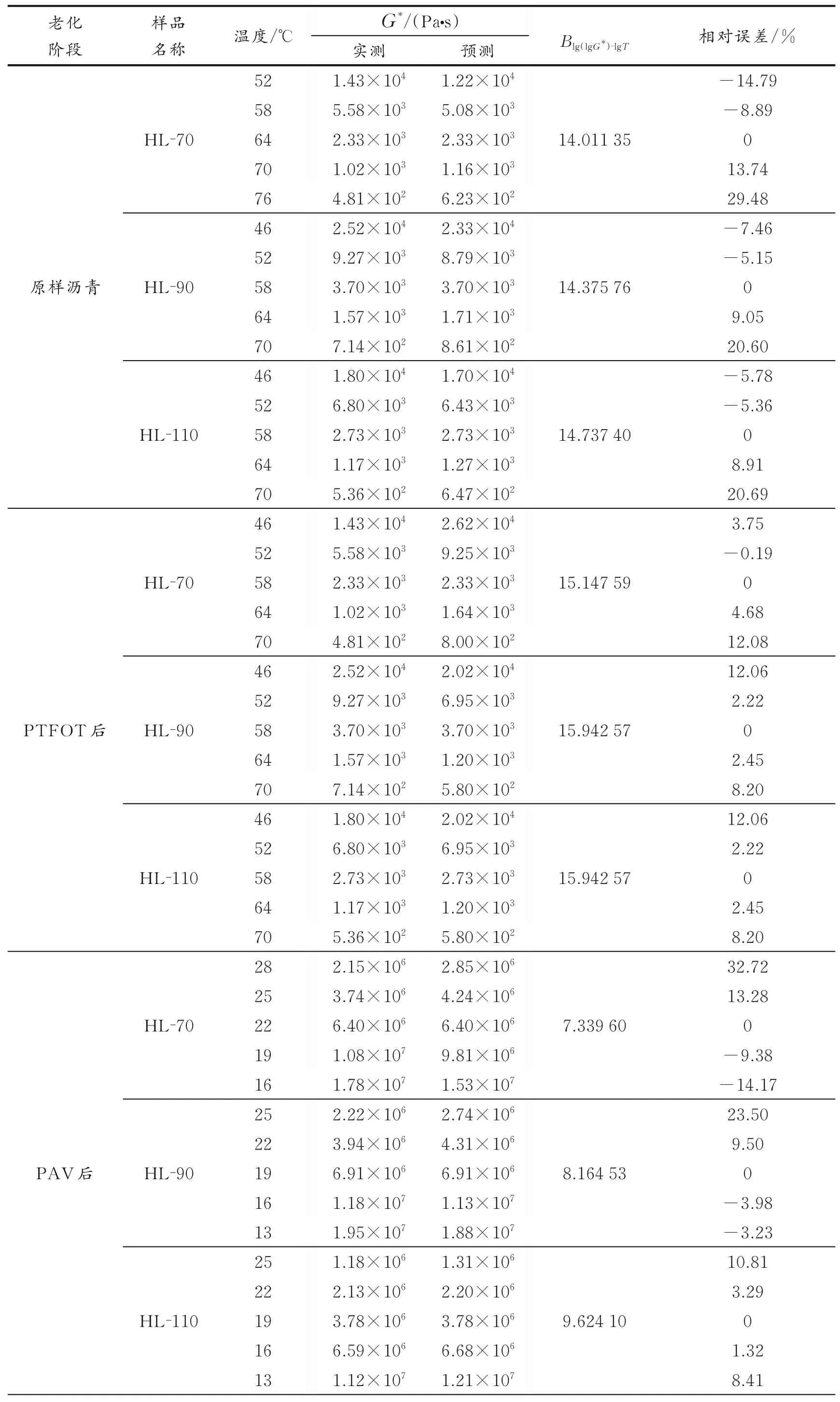
表7 实测复合模量与预测复合模量的对比Table 7 Comparison between testing data and predicted data

根据ASTM D7715-08标准方法的精密度要求，原样沥青G*/sinδ重复性误差为6.4%，再现性误差为17.0%；RTFOT后的沥青G*/sinδ重复性误差为9.0%，再现性误差为22.2%；PAV后的沥青G*sinδ重复性误差为14.2%，再现性误差为40.2%。

假设G*/sinδ或G*sinδ的精密度约等于G*的精密度，原样沥青11个G*数据中相对误差超过17.0%的有2个，其他数据均满足再现性精密度的要求；12个RTFOT后数据相对误差均小于22.2%，满足再现性精密度的要求，不满足重复性误差要求的只有3个数据；PAV后12个数据相对误差均低于40.2%，不满足重复性误差要求的只有2个数据。

通过以上数据发现，数学模型预测的35个数据中，不满足再现性要求的只有2个数据，预测数据基本满足实测数据再现性精密度要求，由此可以判断：在不同老化阶段，分别采用一个测试温度下的复合模量数据，用3个数学模型可准确进行对应老化阶段复合模量的预测。

本研究采用两种不同原油生产的6个牌号共10个沥青进行研究，得到不同老化阶段复合模量和温度之间的数学模型，而验证数据采用第三种与建立模型无关的原油生产的3个牌号沥青，验证结果满足复合模量实验方法再现性精密度的要求，由此证明数学模型具有普遍适用性。本研究采用10个沥青得到数学模型，如果再增加沥青的数量，式（2）中不同老化阶段沥青的k和b有可能会随着样品数量的变化而变化。因此后续研究需要更多的沥青样本，从而得到更准确模型中k和b值。在复合模量与温 度 的 关 系 中，因 为Klg（lgG*）⁃lgT和Blg（lgG*）⁃lgT几 乎 完 全线性相关，所以每一个沥青产品都具有唯一的Klg（lgG*）⁃lgT或Blg（lgG*）⁃lgT，这 说 明 对 于 石 油 沥 青 而 言，Klg（lgG*）⁃lgT或Blg（lgG*）⁃lgT具 有 类 似“基 因”或“指 纹”特性，它虽然是通过复合模量双对数与绝对温度对数回归获得，但对于每个沥青而言，它却是唯一的。复 合 模 量 数 据 越 多，Klg（lgG*）⁃lgT和Blg（lgG*）⁃lgT线 性 方 程越 趋近于真 值。因此Klg（lgG*）⁃lgT或Blg（lgG*）⁃lgT线 性关系的发现，具有重要的理论价值，关于复合模量、温度和Klg（lgG*）⁃lgT或Blg(lgG*)⁃lgT的数学模型的建立将为复合模量与其他与温度密切相关的流变性质之间的关联奠定了基础，也为三个评价体系之间的关联建起了桥梁。

6 结 论

复合模量双对数与绝对温度对数和Klg（lgG*）⁃lgT或Blg（lgG*）⁃lgT之间 的关 联最适合表达复合模量的温度特性；在线性黏弹性区间，石油沥青复合模量的数值由绝对温度的对数和Klg(lgG*)⁃lgT或Blg(lgG*)⁃lgT共同决定。每个沥青Klg(lgG*)⁃lgT或Blg(lgG*)⁃lgT是唯一的，这两个参数具有“指纹”特性。

在线性黏弹性区间，建立了复合模量和温度之间的数学模型。经实测数据验证，用数学模型计算得到的数据满足实验方法再现性精密度要求，通过数学模型预测原样沥青、RTFOT后沥青、PAV后沥青，具有准确性、可行性、普遍适用性。