长江水质综合评价及污染源确定方法研究
邱居华,吕康玄
(1.三峡大学(湖北)设计咨询研究院有限责任公司,湖北 宜昌 443002;2.中交第二航务工程勘察设计院有限公司,湖北 武汉 430060)
0 前 言
长江是中国第一大河,水资源极其丰富,是我国重要的生态安全屏障区。近年来,长江流域水资源的开发程度日益增大,水环境受人类活动干扰程度日趋恶化,水环境污染问题突出。因此,进行长江水质污染的评价和确定污染源十分重要。
随着水环境污染问题日益严重,水质与污染源的合理评价与判断逐渐成为研究热点之一。目前,已有诸多学者对此问题开展了系列研究。Lin tao等[1]使用多元统计技术和综合水质指数(IWQI)对2018—2020年中国广东省茅州河流域的地表水水质进行了评估。Thotagamuwa H.T.B.N等[2]结合土地开发利用与水质的关系对地表水进行了评价。Wu Tao[3]等利用水质综合评价模型对2008-2018年的伊龙湖水质进行了分析。除此之外,朱长军等[4-9]均从不同角度提出了综合评价模型。
另一方面,如何进一步确定河流污染源,对河流生态环境治理与防控有着重要意义。高嵩等[10]以泰州老通扬运河引水工程为例,利用一维河网水动力水质模型来分析论证新建泵站的必要性和规模。王伟等[11]系统介绍了国内外广泛运用的三类水质耦合模型类型,并提出了展望。潘祥东等[12]基于一维水质模型计算了盐津河纳污能力,为盐津河当地水环境治理提供参考和科学依据。周睿等[13]提出了将一维水质模型应用于分离监测断面点源污染负荷和非点源污染负荷的方法。张颖等[14]对里下河地区水质模型进行了研究。然而,以上方法在对污染源进行确定与分析时未给出详细的隶属度函数及权重计算方法。
本文对隶属度函数及权重的计算进行了深入的分析,对长江水质综合评价方法适用性进行了验证,并基于一维水质模型对污染源进行了确定与分析,为水环境治理提供方法依据。
1 模糊综合评价法
根据模糊综合评价方法,可以得到水质综合评价模型如下:
FCI=B×S
(1)
式中:B为各种等级水质出现的可能性;S为描述各类水质危害程度的水质标准类别向量。可分别利用下式求出:
B=W×R
(2)
S=(S1,S2,S3,S4,S5,S6)
(3)
公式(1)~(3)中:W为水质评判因素权重向量;R为隶属度组成的模糊关系矩阵;S这是一个主观因素很强的量,可以人为确定。已知Ⅰ、Ⅱ、Ⅲ类为可饮用水即品质最好危害程度最低,此处根据日常经验可以取S=(1,2,3,4,5,6)。对于式(2)中的W及R是本文所要考虑的重点,最终构造权重矩阵及隶属度模糊关系矩阵如下:
对于权重矩阵,其超标倍数越多权重越大,因此构造其计算方式如下:
W=(w1,w2,w3,w4)
(4)
其中,

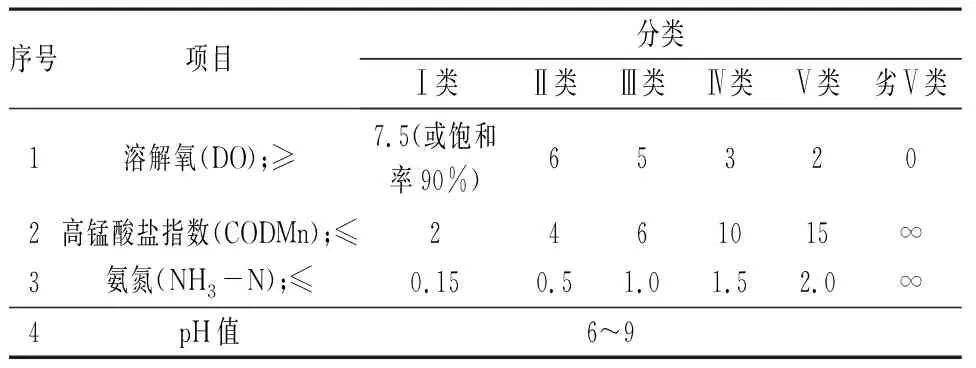
表1 水质标准值 /(mg·L-1)
另一方面,对于由隶属度组成的模糊关系矩阵可得:
(5)
式中:i对j的隶属度 表示第 种污染物的环境质量数值可以被评价为第j类环境质量的可能性。例如:r11表示DO对Ⅰ类水的隶属程度。进而,以表1中污染物的顺序可求得其隶属度的计算公式如下:
对i=2,3,有j=1时为:
(6)
j=2,3,4,5时为:
(7)
j=6时为:
(8)
对i=4,j=1,2,3,4,5时为:
(9)
j=6时为:
(10)
当i=1时,与上面类似,只不过它是逆向趋势,这里不再赘述。这里kij是《地表水环境质量标准》中4个主要项目标准限值。
就本文而言,其水质影响因素集即为U={DO,CODMn,NH3-N,pH},而水质判断集即为水质的不同评价等级组成的集合。V={Ⅰ类,Ⅱ类,Ⅲ类,Ⅳ类,Ⅴ类}。
2 基于一维水质模型的污染源确定方法
已知干流上各观测点每个月份的水流速,但由于水流速度是变化的,它的平均速度很难求出,所以根据上一个站点的水流速度和下一个站点的水流速度来估计这两个站点之间的平均速度,即:
(11)

(12)
各观测点每秒流过长江水中污染物的总量为污染物浓度与单位时间该观测点流量Qij的乘积,所得表达式如下:
mij=nij×Qij
(13)
公式(15)中:mij为每秒流过长江水中污染物的总量,mol;nij为污染物浓度,mol/m3;Qij为单位时间该观测点流量,m3/s。
基于GIS技术的一维水质模型,建立一维河流的污染物浓度与降解系数的偏微分方程为:
(14)
公式(16)中:t为时间,s;C为污染物浓度, mol/m3;k为降解系数;S为污染物源项;E为扩散系数;x为沿河流方向位置。
当流速较大时,污染物的推移作用远大于扩散作用,故可忽略扩散系数不计,同时若假定个污染源排放为连续稳定,且 ,即污染物浓度变化与时间无关,此时一维模型可简化为:
(15)
给定边界条件,则下游断面处污染物与降解系数的函数关系为:
f(t)=mij×e-αtij
(16)
因为一个观测站(地区)的水质污染主要来自于本地区的排污和上游的污水,所以求出上一个站点的污染物降解后的剩余污染物后,可以两个站点之间污染物增加情况,所得表达式如下:
mi(j+1)-f(t)=ni(j+1)×Qij-mij×e-αtij
(17)
3 长江流域水质评价及污染源确定分析
3.1 数据来源情况
长江流域水资源数据和水污染数据均来自2011—2017年《中国统计年鉴》及长江干流7个观测站点的观测数据。
3.2 综合评价结果与分析
利用上述模糊综合评价模型以综合评定值排序的结果得出各地区水污染程度,最终可以判断各地区水质的污染状况,如图1所示。
图1中横坐标1-17代表表2对应的17个区域。其中,各个地区水质的污染状况由小到大的排序如表2所示。

表2 污染状况由小到大排序
由表2可以看出:各观测城市所在的江段的水质污染的情况,水质最差的是江苏南京林;其次是江西南昌滁槎;第三位的是四川乐山岷江大桥地区。水质最好的是湖南岳阳城陵矶,其次是湖南长沙新港地区,第三位的是湖南岳阳岳阳楼地区。可见湖南地区水质保护效果较好,江苏与江西地区水质保护效果较差。
3.3 污染源确定结果与分析
引入一维水质模型,上游污染物呈衰减形式对下游影响,用本地区污染物的量减去上游对下游的影响量及得到本地区排入污染物的量,依次求得各地区排入的污水量进行比较,两种污染物排入量如表3及表4所示。
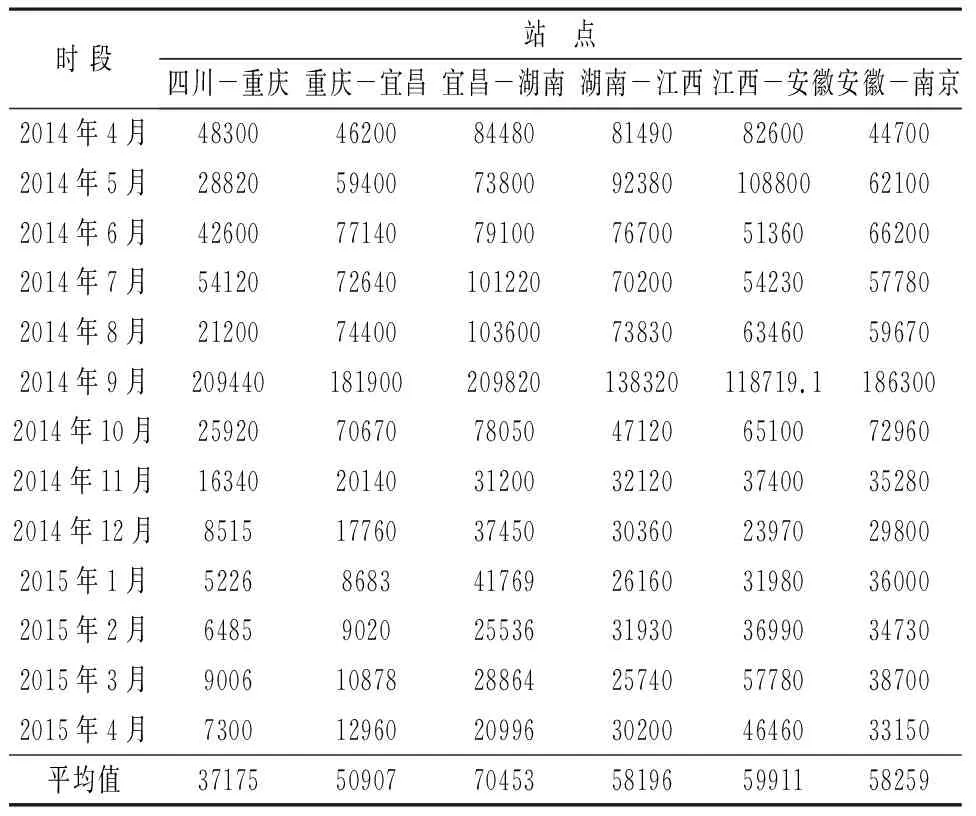
表3 高锰酸盐指数总量 /mol

表4 氨氮总量 /mol
平均值可以反映事物的一般规律,以高锰酸盐和氨氮的平均值变化观察污染物主要集中地,如图2所示。
由图2可以看出,数据值越大说明排放的污染物越多,高锰酸盐和氨氮的排放量都是在湖北宜昌至湖南岳阳这一区段数量最大,江西九江河西水厂至安徽安庆次之,由此可下结论说长江干流近一年多主要污染物高锰酸盐指数和氨氮的污染源主要在湖北宜昌至湖南岳阳、江西九江河西水厂至安徽安庆之间。
通过以上对长江流域污染程度评价及污染源的确定与分析,结果和后期相关报道[15-16]中关于长江流域污染程度及污染物种类高度吻合,由此可见,本文介绍的方法对水质污染的评价和污染源确定问题具有较好的工程适用性。
4 结 论
(1) 本文采用模糊数学的概念建立了模糊综合评价模型,基于一维水质模型提出了一种水质评价及污染源判别的方法,并分析得出长江干流近一年多主要污染物高锰酸盐指数和氨氮的污染源主要在湖北宜昌至湖南岳阳、江西九江河西水厂至安徽安庆之间。
(2) 结合2011—2017年《中国统计年鉴》及长江干流7个观测站点的观测数据对本文方法进行了验证,结果表明该方法可准确评价水质污染程度并有效确定污染源,具有较高的工程适用性,可为长江大保护的水质考核及污染物的确定与治理提供数据支撑与理论参考。

