Spatiotemporal Input Control: Leveraging Temporal Variation in Network Dynamics

Yihan Lin, Jiawei Sun, Guoqi Li,, Gaoxi Xiao, Senior,

Changyun Wen, Fellow, IEEE, Lei Deng, Member, IEEE, and H. Eugene Stanley

Abstract—The number of available control sources is a limiting factor to many network control tasks. A lack of input sources can result in compromised controllability and/or sub-optimal network performance, as noted in engineering applications such as the smart grids. The mechanism can be explained by a linear timeinvariant model, where structural controllability sets a lower bound on the number of required sources. Inspired by the ubiquity of time-varying topologies in the real world, we propose the strategy of spatiotemporal input control to overcome the source-related limit by exploiting temporal variation of the network topology. We theoretically prove that under this regime,the required number of sources can always be reduced to 2. It is further shown that the cost of control depends on two hyperparameters, the numbers of sources and intervals, in a trade-off fashion. As a demonstration, we achieve controllability over a complex network resembling the nervous system of Caenorhabditis elegans using as few as 6% of the sources predicted by a static control model. This example underlines the potential of utilizing topological variation in complex network control problems.

I. INTRODUCTION

NETWORKED structure is a common feature in natural and artificial systems, many of which contain complex topology and higher-order interactions among nodes. The analysis of empirical networks has inspired research fields such as community detection [1], influence maximization [2],and information dissemination, which in return boost applications like epidemic prediction [3]–[5] and recommender systems [6]. Many complex networks are also control systems of practical value [7]–[11], which inspired the study of network control, including theoretical efforts to understand network behaviors under control [12]–[14] and applicationdriven work on specific control solutions or algorithms[15]–[18]. However, part of these efforts are confounded by the complexity originating from network topology, dynamics,and sometimes mere scale [13], [19], [20]. The unprecedented network scale and diversity encountered in modern engineering call for control strategies that are not dependent on specific feature or structure but can handle network complexity in a general way.

Many networks found in nature and human societies show highly dynamic interaction patterns [21]–[24] and are referred to as temporal networks. Among them, there are systems that function robustly under control and can offer inspiration for new control principles. It is suggested that the time-varying topology is essential to a network’s efficiency and flexibility[25]. Although the majority of control problems are studied using approximated linear systems, e.g., the linear timeinvariant (LTI) model [26], [27], there are fundamental differences between a temporal system and what a linear model can capture. An LTI system is governed by the equationx˙(t)=Ax(t)+Bu(t), which assumes slow dynamics of the network connection specified by matricesAandBand approximates them as constant matrices, whereas in the temporal case, the dynamics of these matrices can have a characteristic time scale comparable tox(t) andu(t).

Despite the attractive properties, there is yet to be a general framework to exploit the advantages of temporal structures for network control. Here, we propose a control strategy featuring time-dependent input connection (i.e., node-source connection) and by modeling and simulation, evaluate its potential in controlling large complex networks. Specifically,we consider a model that extends from the linear network model but incorporates a piece-wise matrixBthat shows variable connectivityBkin different time periods:x˙(t)=Ax(t)+Bkuk(t)fort∈[tk−1,tk) (Fig. 1). In this model,the time intervals, the input matrices, and the control input vectors are open to optimization, which resembles the realworld cases where input signals can be directed to different sets of nodes during control [28]–[31]. Here, matrixBis assumed to evolve at a much higher rate than the adjacency networkAitself, andAis modeled as a constant. Despite the simplicity, the model captures the fast and slow dynamics of network structures and is expected to offer clues on the general principles of control with temporal input connections.

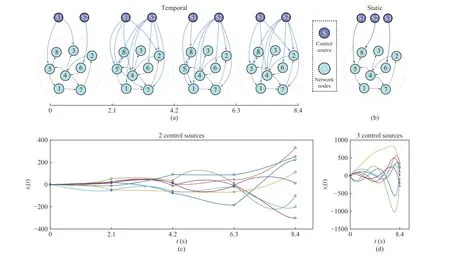
Fig. 1. An example comparing the spatiotemporal input control with static network control. (a)–(b) Schematics illustrating an 8-node network (nodes are colored in light blue; directed edges are represented by black arrows) made controllable by 2 sources (dark blue) in 4 time intervals or by 3 sources via static input connection. (c)–(d) Optimized node trajectories of the 2 control strategies. Although the target is reached at 8.4 seconds in both cases, the spatiotemporal input gives much more compact trajectories.

We term the proposed control strategy instantiated with this model as thespatiotemporal input control, given that it integrates the spatial and temporal patterning of the nodesource connection. It is proved that given a sufficient number of time intervals, controllability can always be achieved with 2 control sources; in many cases, 1 source is sufficient. This lifts the lower bound predicted by the LTI model, which can be computed using the maximum matching algorithm [32].The difference in controllability could be explained by the delivery of control signals to the network: in contrast to the LTI model where all nodes are under effective control [32],[33], the spatiotemporal input controls different subsets of nodes in different time intervals.

We further optimize the input matrices and signals with a proposed semi-analytic method to generate control solutions.By simulating more than 1000 randomly generated networks,we find that the cost of control, or the control energy, drops with the number of intervals and the number of sources. The dependence of energy on intervals and sources could be summarized into a trade-off relationship, where more intervals may compensate for the lack of sources. Practically, this indicates a promising strategy to tackle large complex networks if dividing intervals can be done with a much lower cost than adding control sources. To demonstrate the potential of the method in handling complex networks, we present a test case using the network topology extracted from the nervous system ofCaenorhabditis elegans[34]–[36], and show that controllability can be achieved with fewer than 6% of the nodes computed by the maximum matching algorithm. A fast construction method is proposed to efficiently generate input connections for large networks like this.

II. MODEL

A. Temporal Network Model

Consider the following piece-wise linear model with temporal input connection. Specifically, it contains a constant directed network ofNnodes controlled byMindependent sources. The time duration is split intoKintervals, i.e.,[tk−1,tk),k=1,...,K. For simplicity, we only consider intervals of equal length, giving Δt=tK/Kfor all intervals.The dynamics is determined by the following system of ordinary differential equations:

B. Controllability

A prerequisite for successful control is the system’s controllability [32]. Given proper input, a controllable system can access any target in the RNspace starting from any initial state. In contrast to the LTI system of which controllability is determined by the Kalman rank condition [37], networks with temporal input structure have a slightly different condition of controllability. Assuming that the control sources are homogeneous and can be connected to any node at any time,the following lemmas give the controllability condition of the model in (1).

C. Control Energy as an Objective Function

D. Optimal Control Problem

III. METHODS

A. Constructing Input Connections for Controllability

For a classical LTI network, a graph-based method,maximum matching, gives a node-source mapping that uses the fewest control sources to ensure controllability. However,this lower bound may not hold true for temporal input connections given that a control source can deliver signals to multiple sets of nodes by switching connections across intervals. In this section, the lower bound of control sources is recalculated by constructing input matrices. The following definitions and lemmas are presented for the proof of Theorem 1.

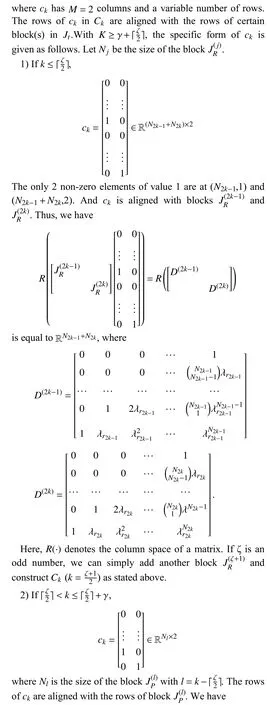
Algorithm 1 Construct Input Matrices If the Adjacency Matrix A Has Complex Eigenvalues{Bk}As{tk}Kk=1 Require: ,{Bk}Kk=1 Ensure:function MATRIXGENERATOR ( , )K ≥γ+「ζ As{tk}Assign 2 ■,γ= β 2 As Jt=P−1AsP Real Jordan canonical form transform of : .Use j as the row number as the Jordan block.k=1 →K kth for do k ≤「ζ if then Cbk=zeros(2,j)2■Cbk[1:2,j]=ones(2,2)Ok=zeros(2,j)Ck=[O1 ··· Cbk ··· Oχ]T end if「ζ 2■+γ ≥k>「ζ if then Cbk=zeros(1,j)2■Cbk[1,j]=1 Ok=zeros(1,j)Ck=[O1 ··· Cbk ··· Oχ]T end if k>「ζ if then Ck=O 2■+γ end if{Bk}Kk=1=P×{Ck}Kk=1 Calculate .Note: the computed should have no more than 2 columns end for end function Bk(k=1,...,K)

Algorithm 2 Construct Input Matrices If the Adjacency Matrix A Has Only Real Eigenvalues{Bk}As{tk}K Require: ,{Bk}K k=1 Ensure:k=1 function MATRIXGENERATORR K ≥ζ(As,{tk})Assign As Js=P−1AP Real Jordan canonical form transform of : .Use j as the row number as the Jordan block.k=1 →K kth for do Cbk=zeros(1,j)Cbk[1,j]=1 Ok=zeros(1,j)if then Ck=[O1 ··· Cbk ··· Oζ]T 1 ≤k ≤ζ end if k>ζ if then Ck=0.end if end for{Bk}K k=1=P×{Ck}K Calculate .Bk(k=1,...,K)k=1 Note: the computed should have only 1 column.end function

B. Optimization

The functionalEin (6) is introduced both as a metric for evaluating the control input and as an objective for problem(7). In this subsection, problem (7) is solved, and in the following sections, the minimized energy is calculated under various conditions to investigate the system’s hyperparameter dependence. This is of practical interest since energy is often an analogy to real-life control effort.

After solving (7), we seek to find a general relationship between energyE, total number of intervalsK, and total number of sourcesM. In order to compare these cases of different hyperparameters, the factors of specific control input, namely {Bk} and {uk(t)}, need to be eliminated by optimization. In other words, it is much less meaningful to compare the energy of systems that are far away from their optima. Therefore, a series of optimal control problems in the form of (7) with differentKs andMs are solved to obtain the minimized energy. Note that the case ofK=1 reduces to an LTI model.

To start with, we have the following theorems and methods for optimization.

Theorem 2:Givenx˙(t)=Akx(t)+Bkuk(t), the input vector minimizingEkof time interval [tk−1,tk) is given by

Hence we have

Proof:Plugging (8) and (10) into (6) yields,

update , = ControlEnergy(A, , , ).^El^Γl{Bl+1 k } tkΛl∂Λ =^ΓlΛl compute .∂E wlk compute projected gradient using (49) and obtain unit vector .¯wlk apply Adam algorithm to determine the step size and update .Δ=∑Λl+1=Λl −µlk¯wlkµlk k −Blk‖+‖Λl+1 −Λl‖compute .‖Bl+1 end while end function k

C. Coordinate Descent Algorithm and Simulation

In order to combine the optimization of the input matrices{Bk}and the vector Λ that are related tox(t) and {uk(t)}, a coordinate descent algorithm is proposed based on the methods described in the last subsection to solve the optimization problem in (38), as shown in Algorithm 3.Specifically, {Bk} and Λ will be updated in an alternating fashion in each iteration. Note that this algorithm also applies to more general cases where bothAandBare piece-wise constant matrices.

To implement the algorithm, {Bk} can be initialized using the constructive methods described in Algorithms 1 and 2 to ensure controllability. In order to avoid converging to suboptimal local minima, we launch gradient descent at multiple initial states with different step sizes and take the case with the lowest energy as an approximation of the optimal solution.As a test case, control energy is optimized for an example network given different numbers of intervals, and a significant decrease ofEwith an increasingKis observed (Fig. 2).

To better illustrate the effect of optimization, a video is provided showing examples of randomly generated networks containing 8 nodes and 10% of all possible connections among nodes (see demo1.mp4). The dynamics of the system is visualized using 4 two-dimensional trajectories representing the state of the 8 nodes. The first and the last 4 nodes are visualized as thexandycoordinates, respectively.

D. Control by Network Partition

It is challenging to solve control problems of large networks. In particular, the computational complexity of the proposed Algorithms 1 to 3 scale with the network size. In addition, the split of time into several intervals also brings about the challenge of temporal complexity to the finite computational resources one can possibly utilize. In this subsection, we discuss the complexity of the proposed algorithms and present a method to circumvent this challenge while constructing and optimizing input connections.

In Algorithm 1, the time complexity of calculating a Jordan canonical form isO(N4) [43]. Other operations in Algorithm 1 are linear except for matrix multiplication, of which the time complexity isO(N3). Regarding space complexity, the most costly operation is also calculating the Jordan canonical form,whose complexity is bounded byO(N2).

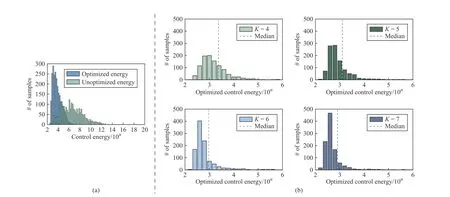
Fig. 2. More time intervals result in lower control energy in randomly generated 8-node networks. (a) Histograms of control energy before and after optimization using the proposed coordinate descent algorithm. Networks are randomly generated and are driven from the origin to the same target state within K = 4 time intervals. Although the specific network topology has a substantial impact on the energy, the algorithm overall reduces energy by multiple orders of magnitude. (b) Histograms of optimized energy of more than 1000 randomly generated 8-node networks given different number of time intervals. The total time is divided into K = 4, 5, 7 or 8 intervals. The increase in the number of intervals significantly reduces control energy.

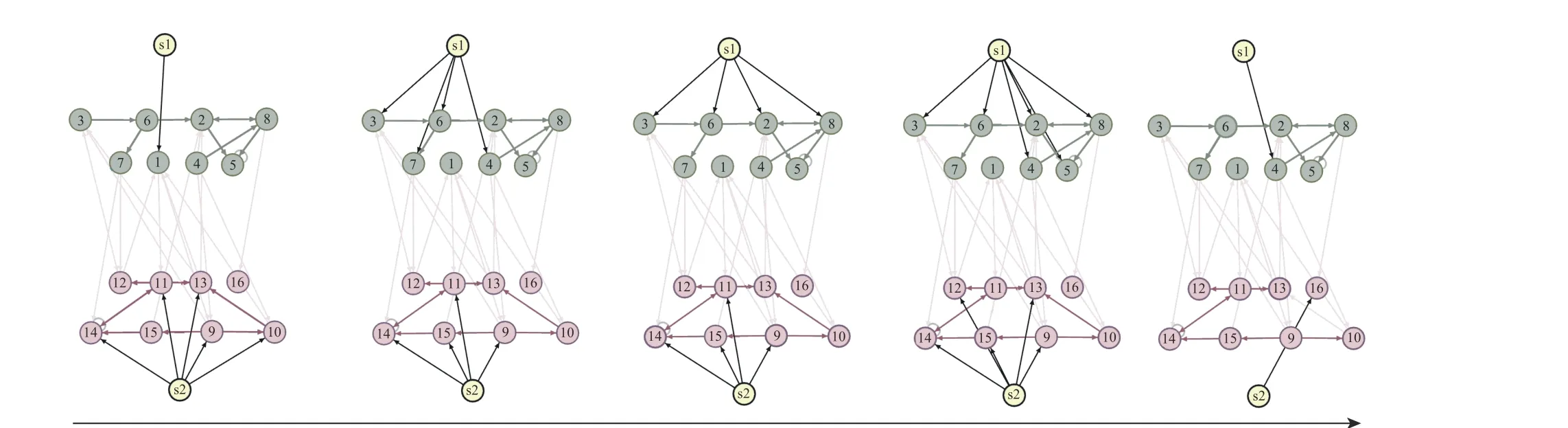
Fig. 3. An example illustrating the method of control by network partition. A 16-node temporal network is split into two 8-node subnetworks (shown in green and pink), with each controlled by one input source (s1 or s2). The 2 subnetworks, with the internal edges (blank arrows), are controllable in 5 time intervals.The combined 16-node network is also controllable regardless of the edges connecting the 2 subnetworks (grey allows), which is consistent with Theorem 5.

The time complexity of Algorithm 3 is hard to determine due to the nonlinear operations such as numerical integration and matrix exponential, which is also dependent on numerical precision. When ignoring the unpredictable iterative steps of gradient descent, the theoretical time complexity is bounded by the calculation of the energy gradient, which isO((NK)3×N×M×K)=O(N4K4M). The space complexity isO(N2K2), which is due to the storage of the gradient.

Remark 1:Note that the above theorems only guarantee structural controllability [45], [46], which is a slightly weaker condition than controllability. However, it is practically useful for controlling a temporal network model, since the probability of having a set of weights that make a network with structural controllability uncontrollable is often 0. Thus,without solving the original optimal control problem, which can be costly, we may instead solve a series of simpler optimal control problems based on the partition of the large network, although the performance of the combined input signals and connections may vary according to the partition.Nonetheless, this indicates the possibility of controlling a large-scale network by controlling parts of the network, and the general methodology is not limited to temporal networks.

IV. NUMERICAL EXAMPLES

A. The Trade-Off Between Energy, Time Intervals and Input Sources

So far, the results regarding controllability and energy in the above sections suggest two pairs of trade-offs, namely betweenKandMand betweenEandK. Here, by simulating an example network, we investigate the relations between energy and the two important hyperparameters, in search of general principles governing temporal network control. By solving the optimal control problems with various combinations ofMandK, we are able to approximately determine the minimal energy in each case, based on which we provide a visualization of the hyperparameter space by fitting a 2D surface from the discrete data points (Fig. 4).Although the results are based on a simple network model, it may explain the power of temporal input connections, which can be partly boiled down to the trade-off among energy,sources and intervals. Compared with static input connections,the spatiotemporal input introduces an extra dimension ofKto the hyper-parameter space, allowing new possibilities of reducing energy or the total number of sources.

B. A Test Using the Neural Network of Caenorhabditis Elegans

Complex networks, a common structure studied across fields, typically have a large size and a non-trivial topology.Here, we consider the applicability of the spatiotemporal input as a general strategy for controlling such networks.Particularly, based on the above-mentioned trade-off relations,we focus on the choice ofMandKin search of a proper balance.

A biological network from the nervous system ofC. elegansis used as an example. Its complexity and the extensive research on its cellular connections make it a perfect test case[46]. It is known to be a sparse network of 2177 nodes and 4007 edges (multiple edges are counted as 1 if they are between the same 2 neurons). In the simulation, the network is treated as a directed graph, while the biological context is neglected. First, we demonstrate the feasibility of achieving controllability and optimizing control over a small 30-node subnetwork. Then, we show how the entire network can be controlled by a small number of control sources. The partitioning method introduced in the previous section is applied to the full network.

Fig. 4. (a) Visualization of the trade-off relationship among energy, the number of sources, and the number of time intervals. The solid dots represent simulation results from an 8-node example network, while the circles are obtained by spline interpolation from the simulated data points due to limited computational power. (b) Projection of (a) on the M-K plane. The dashed line in the lower-left corner shows the boundary of controllability. (c) Projection of (a)on the E-K plane. (d) Projection of (a) on the E-M plane.

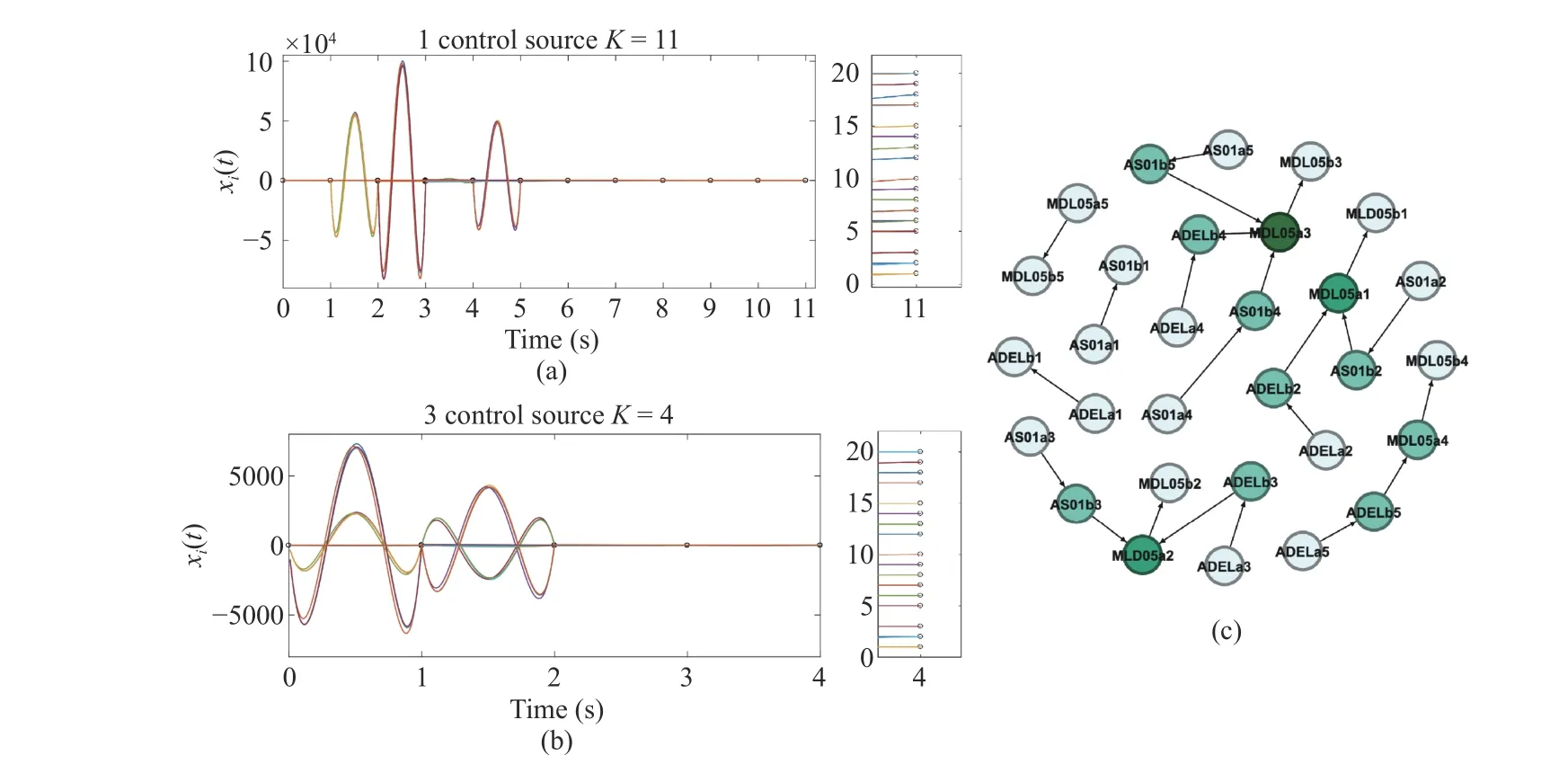
Fig. 5. Optimized trajectories of a 30-node sub-network extracted from the nervous system of C. elegans. (a)–(b) Trajectories of all 30 nodes controlled by 1 or 3 sources, respectively. The right panels provide zoom-in views near the target states, to which the relative error of each node is contained within 0:1%. (c) A graph of the sub-network. The nodes are labeled by their cellular code in [47]. Each node is colored differently according to its degree.

1) Test on a Subnetwork:A small subnetwork of 30 cells with sparse connection is extracted from the large neural network of an adultC. eleganshermaphrodite. The cells include ADELa1～ADELb5, AS01a1～AS01b5, and MDL05a1～MDL05b5, which together form 23 edges in total,with an average in-degree of 0.756 (Fig. 5(c)). According to Theorem 1, the network is controllable by 1 source. A set of input matrices {Bk} are generated that spans acrossK=11 intervals. The optimal control problem is solved, giving the trajectories in Fig. 5(a). Another set of parametersM=3 andK=4 yield a much lower energy after optimization (Fig. 5(b)).In contrast to these cases, the maximum matching algorithm predicts a lower bound of 11 sources connected to cells ADELa1, ADELa2, ADELa3, ADELa4, ADELa5, MDL5a5,AS01a1, AS01a2, AD01a3, AD01a4 and AD01a5,respectively.

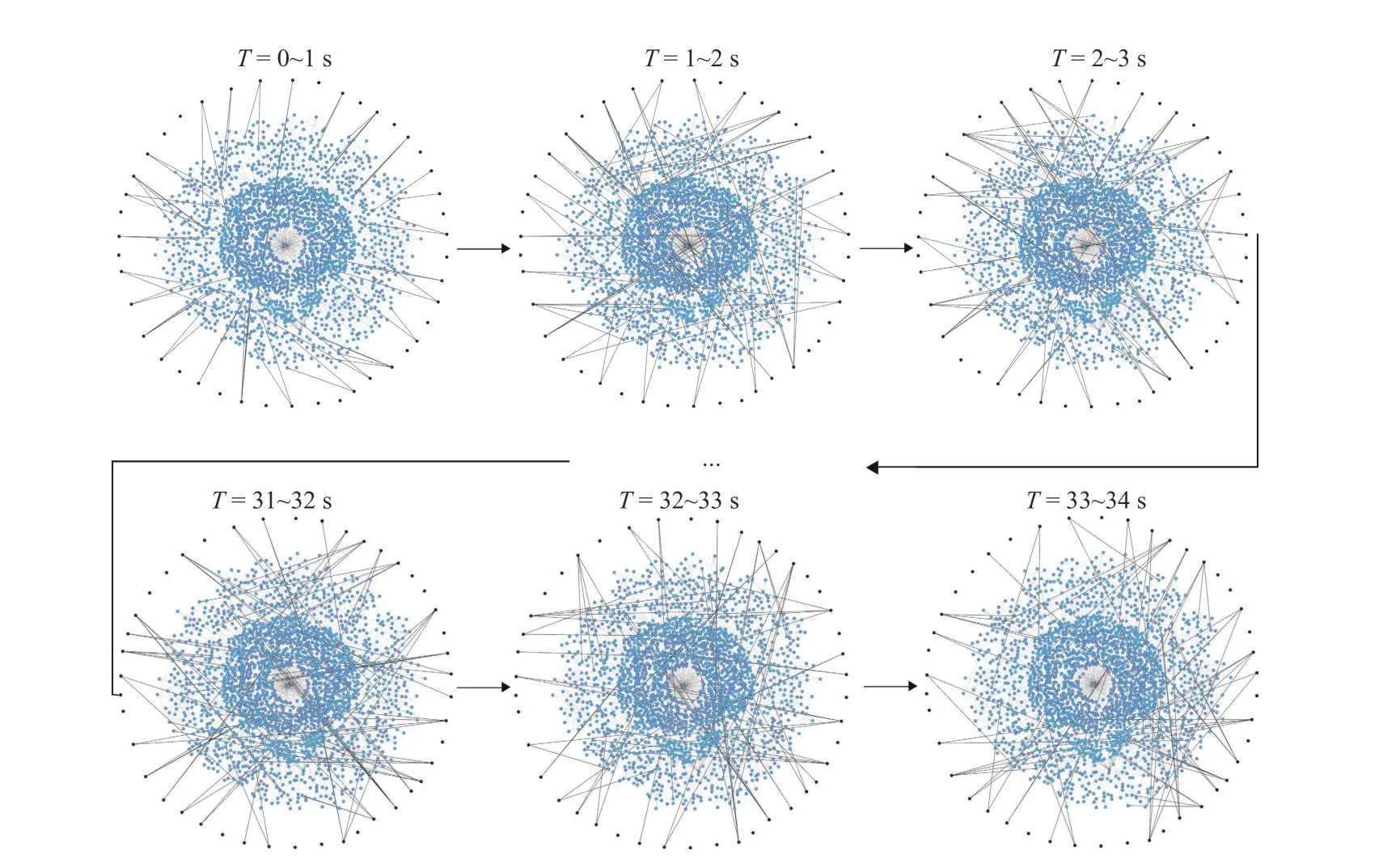
Fig. 6. Graphical demonstration of the node-node and node-source connections in the controlled neural network of C. elegans. The first and last 3 intervals out of 34 are shown here. The nodes and the sources are colored in blue and black, respectively. Each interval is of 1 second. See connection.mov in the supplementary materials for more details.

It is noted that given 3 sources, ‖x(t)‖ is smaller by roughly an order of magnitude on overage than the 1 source case,while the overall “complexity” of control input, which can be thought of asM×K, is similar. It is possible that a non-trivial interplay exists between the numbers of sources and intervals in terms of energy scaling, which requires further studies.

2) Test on the Entire Network:It is important to understand how nature exploits limited resources and energy for efficient manipulation of complex systems. In living matter, it is reasonable to speculate that systems deliver or respond to control signals in a time-dependent fashion with only a small number of sources being used or activated at the same time,given examples like the sparse and temporal firing patterns in cortical activities [48]–[51]. Here we show that in agreement with this intuition, the spatiotemporal input can achieve controllability over the entire network of 2177 nodes by frequently switching the connections from a limited number of sources.

According to Fig. 4, we can balance the numbers of sources and time intervals given a certain level of energy. For small networks, this can be done by generating random instances of{Bk}until the controllability condition (3) is satisfied. Here,given a large network, we construct input connections by the method of network partition, as introduced in the previous section. For each subnetwork, the input connections are generated by Algorithm 1 or 2.

The full network is split intoR=44 subnetworks, each of which is controllable by 1 source, givingM=R=44. This results inK=34 time intervals. The node-node and nodesource connections are illustrated in Fig. 6. Controllability is tested directly using equation (3). As a comparison, the same network requiresM≥754 nodes if controlled by static input.Therefore, the spatiotemporal input strategy saves more than 94%of the control sources. It is worth noting that there are numerous ways of partitioning the network, and the decision will likely be reflected in the control energy.

To accelerate the simulation, we increaseRto 223 and still assumeM=R. The network is controllable withinK=5 intervals. Although we have successfully achieved controllability, the trajectories are not optimized due to the incapability of the optimization algorithm to overcome network scaling, which is a typical phenomenon for gradient descent algorithms, known as the curse of dimension. Due to the limited computational resources, it is difficult to achieve an optimal result within an acceptable amount of time.Instead, a few iterations of gradient descent are carried out for partial optimization (Fig. 7(a)). A short animation(connection.mov) is provided in the supplementary materials to show the temporal sequence of the node-node and nodesource connections for this case.

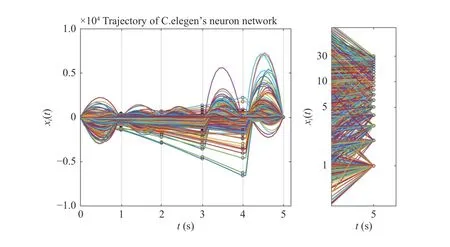
Fig. 7. Simulated dynamics of the C. elegans neural network controlled by 223 sources in 5 intervals. The target state is randomly generated. Trajectories for 2177 nodes are plotted in different colors. A zoom-in view near the target state is provided in the right panel, underlining the accuracy of the control process.

V. CONCLUSIONS

This work explores the idea of using temporal input connections in complex network control. Specifically, a piecewise linear model is studied, which yields a novel control strategy termed the spatiotemporal input control. Regarding controllability, we prove that as few as 2 input sources are sufficient for an arbitrary network given sufficient intervals.Regarding the energy cost of control, we show by simulation that having more intervals can effectively reduce control energy after optimizing the input. Further simulation suggests that the advantage of temporal topology may be attributed to the trade-offs between energy, control sources and time intervals. By making the input matrix temporal, we are essentially introducing an extra dimension of intervals to the hyperparameter space, expanding the space of possible control solutions. It is worth noting that although the above properties are revealed with a relatively simple model, the trade-off relationships may generally apply to different forms of temporal topology.

The example of theC. elegansnervous system underlines the potential of temporal input connections in controlling large networks. In real-world applications where the time intervals can be engineered, this strategy can prevent the number of input sources from scaling proportionally with the network size and thus becoming unaffordable. However, solving the optimal control problem can pose challenges on computational resources due to the time complexity and the gradient descent method. It remains an interesting problem to develop a faster algorithm for optimizing the temporal topology in general.

In summary, the paper contributes a) conceptually by suggesting a shift from static to temporal input connections,which is tested with a piece-wise linear model; b) theoretically by proving that the lower bound of the number of input sources can be relaxed to 1 or 2, and presenting the trade-off relationship among energy, sources and intervals; c)methodologically by solving the optimal control problem for temporal networks and presenting the methods for constructing temporal input matrices. The results suggest a promising control strategy for complex networks and a possible explanation for the highly efficient control systems observed in nature. The methods proposed with our model may also be of practical value in future applications.

APPENDIX

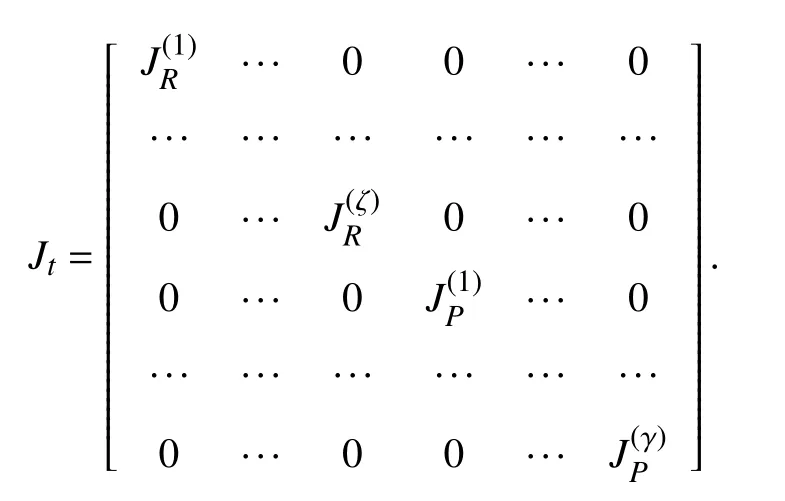
And according to Lemmas 1 and 2, the controllable space of the system in (1) is