不同数据处理方法在高密度电法水库渗漏成像中的应用

李 进，王小明，谭 磊

(1.南京市水利规划设计院股份有限公司，江苏 南京 210022；2.苏交科集团股份有限公司，江苏 南京 210000；3.浙江省水利河口研究院(浙江省海洋规划设计研究院)，浙江 杭州 310020；4.浙江省水利防灾减灾重点实验室，浙江 杭州 310020)

1 引 言

地球物理勘探是通过采集到的多物理场数据体来认识地下空间的地层构造、矿产赋存、灾害分布以及工程地质环境等[1-4]，具有高效、无损、透视、大数据的特点，在宏观调查和精细勘探中都有着突出的优势，与钻探手段相比，二维、三维的探测成果能连续的反映出勘探区的地质情况，极大地提高了勘探密度[5,6]。但是，受限于野外工作环境、地形条件以及时间成本等因素的制约，在权衡精度与效率利弊的情况下，提交的物探图像往往是适度特征点数据经网格插值处理后的成果。目前，不规则离散数据网格化运算的插值技术较多，如美国Golden Software公司的商业Surfer系列软件中就有12种不同类型的插值方式[7]，丰富的插值功能为数据显示提供了便利，但具体到每种插值算法在数据可视化表达方面也存在一定的差异性。近年来，一些物探学者也针对不用插值算法的应用及特点方面作出许多有益的工作。吴卫国[8]利用Surfer软件的克里金法对水系沉积物数据进行数据网格化，并结合白化功能减少离散数据的外推；刘晓霞等[9]推导了Kriging球面应变计算公式，交叉检验及残差分析结果表明，速度场滤波和网格插值是可效的；姚文等[10]以某磁铁矿区高精度磁测数据为例，在比较了5种网格化平面图的基础上，认识到在保证网格化的精度和等值线圆滑的前提下，克里金插值法和最小曲率法网格化效果最好；王咸彬等[11]在总结了常见散乱数据插值方法的基础上，采用克里金插值方法把实测测井数据插值成反演的三维速度场初始模型；郭崇光[12]采用Surfer软件中的克里格方法对电测深数据进行网格化，并指出具体插值中的注意点。

高可靠度的原始数据是地球物理探测数据网格化成像的基础，然而在观测过程中显然不能排除外来噪声的干扰[13]，因此有必要采用一定的手段对网格数据体进行滤波降噪处理。李文杰[14]运用二维自动调平处理了频率域航空电磁数据的零漂误差，提高视电阻率和平面剖面图质量；余金煌等[15]采用小子域滤波技术对高密度电法探测的抛石层图像进行增强处理，提高了图像精度和可读性；黄基文[16]根据基阶模态与高阶模态面波之间视速度存在差异，利用二维数字滤波法进行分离；王瑞雪等[17]把均值滤波、中值滤波以及小波变换对测井电导率数据进行滤波处理。近年来，高密度电法在水库大坝渗漏隐患探测中得到广泛应用[18]，但较少研究不同插值方法对电阻率图像上隐患的优化识别，并且涉及到具体滤波方法的差异性以及相应参数设置等内容还需进一步探讨。为此，本文以水库大坝蚁穴渗漏高密度电法探测数据为试验对象，比较了多种网格插值方法图像的差异性，并对自然邻点法插值图像中的滤波方法及插值结果进行分析，从而得到适合于土石坝电阻率可视化表达的成像技术，以此提高隐患的识别能力及效果。

2 试验工程概况

浙江某水库始建于1957年10月，并于1958年7月建成蓄水，坝址以上集雨面积0.301 km2，总库容为16.395万m3，正常库容为12.149万m3，灌溉面积720亩，是一座以灌溉为主的小(2)型水库。大坝坝型为类均质坝，坝顶高程为55.70 m，坝顶长为103.5 m，最大坝高7.58 m，坝顶宽3.0 m，坝顶铺广场砖。

该水库已服役运行60多年，大坝防渗结构存在不同程度的老化，尽管多次对大坝进行加固处理，但在极端天气作用下，于2019年在大坝左坝段出现渗漏、塌陷的突发险情，为尽早排查出大坝渗漏的原因以期保障水库的安全运行，采用高密度电法对水库大坝渗漏原因进行探测，并对异常区进行防渗处理，在灌浆过程中大坝迎水坡、背水坡均出现局部的冒浆现象，与探测得到的渗漏通道走向基本吻合。以此探测数据为基础，从不同插值方法、滤波分析等角度，提升对探测成果的可识别性。

图2是地下记录视电阻率值的散点分布图，记录点数据共有946个，最小电阻率值为11.98 Ω·m，最大电阻率值339.15 Ω·m，均值95.93 Ω·m，中值86.39 Ω·m。

图1 试验现场示意Fig.1 Schematic diagram of the test site

图2 原始数据记录点分布Fig.2 Distribution of original data recording points

3 电阻率数据插值及滤波处理方法

3.1 常用数据插值方法的简介

数据的网格化处理工作是空间离散测点原始数据可视化成像的基础，在高密度电法勘探过程中，水平方向上各个电极测点的最小间距是保持固定的，垂直方向上相邻深度点的距离又与水平长度有关，并且随着深度不断的加大，水平层间的测点呈等差数列不断减少，总体表现为矩阵排列的形式。因此，为把纵、横向上数据点之间的变化趋势反映出来，对原始数据采用网格化插值是重要的环节。在地球物理数据网格插值方面应用较多的方法[19]，通常有反距离加权插值法(Inverse Distance to a Power)、克里金插值法(Kriging)、最小曲率插值法(Minimum Curvature)、改进谢别德插值法(Modified Shepard’s Method)、自然邻点插值法(Natural Neighbor)、最近邻点插值法(Nearest Neighbor)、多项式回归插值法(Polynomial Regression)、径向基函数插值法(Radial Basis Function)、线性插值的三角剖分插值法(Triangulation with Linear Interpolation)、移动平均插值法(Moving Average)、数据度量插值法(Data Metrics)、局部多项式插值法(Local Polynomial)12种方法。同一组数据采用不同的插值方法，图像中有用信息的显示程度也存在差异，因此有必要通过比较选择最优的插值方法[20]，从而指导工程应用中的数据处理。

3.2 常用网格滤波方法

数据网格化处理有效预测了测点之间的数据体，但不能消除原始信号中的噪声信息。高密度电法数据噪声来源复杂，包括天然电场、游散电流、接地不良、地形起伏以及仪器杂音等[21]，外来噪声往往会降低数据信号的信噪比，从而降低图像信息的真实度以及图像自动识别的能力。因此，开展网格化数据体进行滤波工作对水库大坝隐患的识别十分重要，但如何选择适合于电阻率成像的滤波方法成为图像可视化的关键。常用的滤波器分为线性滤波器和非线性滤波器，并且线性滤波器中有滑动平均滤波、距离加权平均滤波、反距离滤波、高斯低通法等。

4 结果分析

4.1 不同插值方法的网格化结果及分析

图3是12种插值方法网格化后的电阻率图像，所有图像采用相同的色阶归一化。从图像上可以直观看出，不同的插值方法得到的电阻率值图像存在较大的差异，主要表现在经插值后的电阻率范围、分布以及图像的平滑度等。其中，多项式回归插值法、移动平均插值法、数据度量插值法以及局部多项式插值法平滑度较大，不能有效揭示出大坝的电阻率值分布，不适合运用在水库渗漏探测的高密度电法数据处理中；反距离插值图像上出现较多的“牛角眼特征”，不利于对隐患的识别；改进的谢别德插值对图像的边界处理较差，局部出现负值，不符合电阻率的物理意义；最近邻点法插值在图像上形成连续的网格，网格之间的连续性较差；最小曲率插值的视电阻率范围为8.29～518.94 Ω·m(表1)，比实际测量最大值339.15 Ω·m高约34.6%；线性插值的三角剖分插值中的电阻率值也出现负值。克里金法、自然邻点法以及径向基函数插值法图像电阻率等值线平滑度较好，插值后的电阻率值与原始值范围基本吻合，在测线上18～24 m段、核心深度3 m的高阻闭合区域与隐患位置基本一致，总体上能反映出大坝地下结构的分布特征，也表明高密度电法在探测土石坝隐患中结果可靠度高。但是，自然邻点法插值外延性较差，克里金法、径向基函数插值能向无值区外推出电阻率的变化趋势，但计算时间较长。因此，水库渗漏高密度电法原始数据的插值优选采用自然邻点法，其次是克里金插值法、径向基函数插值法，在工程应用中采用合理的插值算法能更加真实地反映出大坝的电阻率变化特征。

图3 不同插值方法的电阻率Fig.3 Resistivity plots of different interpolation methods

表1 不同插值方法的电阻率范围

4.2 不同滤波方法的等值线结果及分析

地下空间的地电场信号频率较低，因此应采用低通数字滤波器对电阻率图像进行噪声处理。根据多种插值算法网格化成果的比较，采用自然邻点插值的电阻率值进行滤波比较分析。图4(a)是不进行滤波处理的等值线分布图，在图像上存在局部极值的小圈闭，并且线条平滑度较差；经滤波处理后的图像，图中的噪声信号明显得到降低，滑动平均、距离加权法的滤波效果相对更好。

图4 不同滤波方法的等值线Fig.4 Contours of different filtering methods

从滤波后的电阻率值范围(表2)上来看，滤波之前的电阻率范围为23.01～336.22 Ω·m，经滤波之后高、低极值得到削减，其中滑动平均滤波电阻率范围相对更收敛，有效降低了噪声对数据的影响。

表2 不同滤波方法的电阻率范围

4.3 不同过滤器尺寸的滤波结果及分析

数据滤波的效果不仅与滤波器的选择有关，而且过滤器尺寸的大小也会对滤波效果产生影响。图5是在垂向-3 m的横向上以及水平24 m纵向上的电阻率变化图。由图5可知，过滤器尺寸越小，滤波效果越差，在曲线上的极值点处变化幅度越大，但随着尺寸的增大，曲线的平滑度增加，从而导致相邻异常区的边界变得模糊。因此，在对水库渗漏的高密度电法数据采用滑动滤波时，过滤器的尺寸7×7。

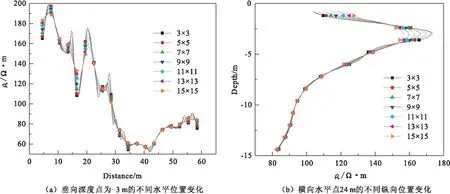
图5 不同过滤器尺寸的电阻率变化Fig.5 Resistivity variations of different filter sizes

4.4 不同迭代次数的滤波结果及分析

滤波的迭代次数大，则可以提高等值线的平滑程度，但过于采用多次滤波计算也可能降低对异常区的识别。图6是在垂向-3 m的横向上以及水平24 m纵向上的电阻率变化图。从图像上可以看出，当迭代次数为1时，电阻率曲线在极值点变化强烈，同时在曲线上有所偏离；当迭代次数为7时，电阻率曲线明显过于圆滑，在拐点位置电阻率的幅度过小，对异常区边界的确定带来不利影响。综上所述，在对水库渗漏的高密度电法数据采用滑动滤波时，迭代次数采用4次。

图6 不同迭代次数的电阻率变化Fig.6 Resistivity variation of different number of iterations

5 结 论

1)高密度电法数据经网格化插值处理后能够把测量点可视化显示出来，有利于评价地质体的电阻率分布，建议在网格化插值中优先选用自然邻点法，其次是克里金插值法、径向基函数插值法；

2)不同滤波方法、过滤器尺寸以及迭代次数对网格化数据的去噪效果存在差异，水库大坝隐患的电阻率滤波优先选用滑动平均法，过滤器尺寸的行列均为7，迭代次数为4次；

3)水库大坝隐患类型复杂，电阻率等值线形态及大小也存在差异，在具体使用时，应对不同电阻率分布特征的可视化方法进行综合比较，从而提高对不良隐患的识别能力。