基于改进SOA-VMD 的磁声发射信号去噪算法

傅伟成，吴 伟，邱发生，李 喆

（1. 南昌航空大学无损检测技术教育部重点实验室，南昌 330063；2. 中国航发沈阳黎明航空发动机有限责任公司，沈阳 110043）

引言

磁声发射（Magnetic acoustic emission，MAE）［1］是近年发展起来的一种磁性无损检测技术。 MAE是铁磁材料中磁畴在交变磁场作用下，由于磁致伸缩效应产生弹性波的现象。分析MAE 信号特点，可以对铁磁材料进行无损检测构件应力评估和微观损伤检测。

MAE 信号对许多材料和力学性能都很敏感，如晶粒尺寸、碳含量、晶体结构、外加张力、残余应力和塑性变形。国内外学者对MAE 信号进行了大量研究，Makowska 等［2］通过MAE 信号对P91 钢的机械性能进行评估，发现无损检测和破坏性测试所得参数间存在一定关系。Astudillo 等［3］对核电站压力容器用A508 级锻造钢的MAE 信号进行分析，确定了材料的磁各向异性、组织和微观结构之间的联系。金亮等［4］根据电磁超声换能器和MAE 技术两种检测方法的原理特性，实现电磁超声换能器对铁磁材料的MAE 检测。

MAE 信号具有非稳态、复杂性、随机性和衰减性的特点，所以需要对信号进行降噪处理，来提高该检测技术对应力和材料表征的鲁棒性和重复性。小波分析广泛应用于此非线性信号处理领域，王雨虹等［5］针对随机非稳态的煤岩体声发射信号，使用基于小波变换的去噪算法，有效提高了声发射信号的信噪比，降低均方误差。但选取不同的小波基函数会对降噪效果产生影响［6］。经验模态分解［7］（Empirical mode decomposition，EMD）算法是以原数据为“基”的自适应处理方法［8］。刘东瀛等［9］利用EMD 与相关系数原理对旋转机械碰摩声发射信号降噪，但EMD 在运算时容易出现模态混叠现象。随后，一种新的时频方法——变分模态分解［10］（Variational mode decomposition，VMD）被广泛关注，VMD 是一种完全非递归模型，其解析信号的瞬时频率具有实际的物理意义，避免了EMD 出现模态层叠的问题，广泛用于此类非平稳复杂信号处理中［11-12］。目前针对VMD 的研究大多是直接使用进行信号处理分析［13-14］，然而VMD 算法需要预设参数惩罚因子α和模态分解个数K值，设置不当参数会导致信号过分解。

海鸥优化算法（Seagull optimization algorithm，SOA）相对于其他如麻雀算法、蝙蝠算法、退火算法等具有更强的全局搜索能力和易于实现的特点［15］，使得它可以适用于参数寻优。本文使用海鸥算法结合变分模态分解对MAE 信号进行去噪处理，利用柯西变异算子在海鸥算法迭代过程中设置随机扰动方法，以幅值谱熵值为适应度函数优化VMD 模态分解个数K和惩罚因子α两个参数，解决海鸥算法迭代过程中容易出现集聚倾向而陷入局部最优解的问题［16］，进而使改进后的算法具有更强的降噪能力。

1 MAE 信号采集

铁磁性材料在交变电磁场激励下，内部磁畴翻转运动，产生磁致伸缩效应，并以弹性波形式向周围传播声信号现象，这些信号特点是低振幅高频率（50 kHz～1 MHz），称为磁声发射信号。

搭建MAE 信号采集系统如图1（a）所示，该系统主要由激励线圈、激励源、功率放大器、MAE 检测探头和MAE 信号放大器组成，其实物图如图1（b）所示。图1（b）中激励源通过功率放大器输出频率10 Hz，电压峰峰值为15 V 的正弦激励信号作用于两个赫姆霍兹线圈上，赫姆霍兹线圈产生磁场用磁化工件，工件产生磁声信号。在工件上施加耦合剂后使MAE 检测探头紧密贴合在工件上，探头将采集到的信号经MAE 信号放大器增益60 dB，通过信号采集卡以2 MS/s（S 为采样点）采样率将数据存储在PC 机中以便后续处理。

图1 MAE 信号采集系统及实物图Fig.1 MAE signal acquisition system and physical diagram

文献［17］指出，MAE 信号强度与材料非弹性应变体积成比例，无论引起非弹性应变的应力是外部载荷还是内部残余应力，应力越大，MAE 信号幅值越低。此外受激励源信号、电磁场大小、探头与工件耦合程度等不确定因素影响，MAE 信号呈现非平稳、衰减性的特点。

对于MAE 信号，包络线可以更确切地描述其特征，信号包络线本质是信号的动态界限，代表了信号动态变化趋势。例如偏斜度反映了随机信号分布歪离标准对称分布的偏斜程度，此外上升时间，持续时间等信号特征参数，直接反映了检测材料的重要物理参数（残余应力、形变机制等），都可以从MAE 信号包络线上获取。图2 为实际MAE 信号波形图，可以看到MAE 信号底噪明显，尾部细节难以区分。再对MAE 信号进行包络线拟合，发现图2 所示包络线由于噪声的干扰，振荡明显，尤其是尾部凸起严重，对后续提取MAE 信号特征值造成很大干扰，必须进行降噪处理。

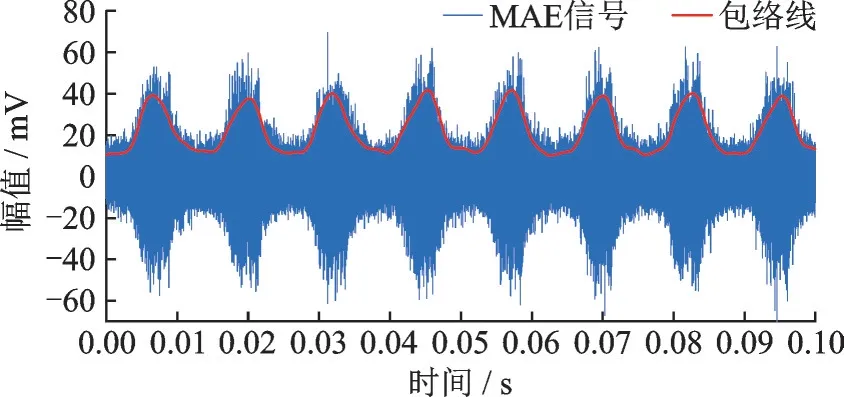
图2 MAE 信号波形图Fig.2 MAE signal waveform

2 CVSOA-VMD 去噪方法原理

2.1 SOA 算法模型

SOA 是基于海鸥攻击在海上迁徙鸟类的行为推演出的群智能优化算法，由以下两种模型组成：

（1）迁移模型。此模型重点在于避免相邻海鸥之间的碰撞。

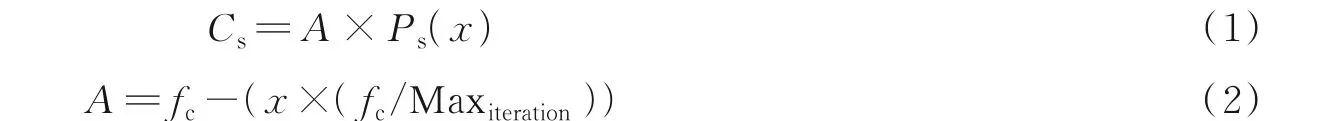
式中：Cs为海鸥种群所有个体相互分散位置，Ps代表海鸥个体所处位置，x为当前迭代次数，A表示可以在一定范围内海鸥的运动行为，fc为控制运动行为从fc慢慢减小至0 的常数。

更新完海鸥位置后，海鸥个体会根据记录的当前最优值（最适宜生存）方向移动。

式中：Ms表示海鸥个体所处位置Ps向记录的当前最优值（最适宜生存）位置Pbs移动路径；B的取值是随机的，它可以适当地平衡搜索和扩展行为；rd为一个随机数，范围是［0，1］。

同时，海鸥个体根据运动路径向着最优值位置进行移动。

式中Ds表示海鸥个体与最优值海鸥个体相对位置。

（2）攻击模型。此模型决定海鸥在搜寻过程中可以根据之前的经验持续变化进攻切入角和进攻速度，进攻行为呈螺旋形。运动行为x轴、y轴、z轴分量分别如式（6～8）所示。

式中：r代表进攻行为时每一螺形圈半径；k代表[0 ≤k≤2π]内随机数；u和v为常数，用来定义螺旋形状。更新海鸥位置为

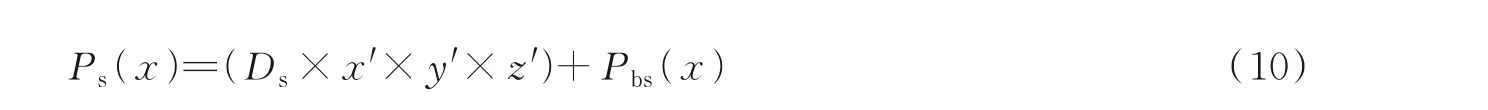
Ps(x)存储历史最佳海鸥位置，并影响下一次迭代种群海鸥位置。

SOA 种群位置最初是随机生成，在搜寻迭代过程中产生最佳位置后，其他海鸥根据最佳位置调整自身运动路径。因此，SOA 被认为是一个全局优化算法，它具有良好的搜索能力。

2.2 柯西变异海鸥算法

如式（11）所示，海鸥种群更新位置时算子被Pbs束缚，计算范围容易被固定在某个区域，从而在后续迭代过程中Pbs始终不变，影响了结果的多样性，即陷入局部最优，这对于一个群智能算法是不利的。

一般来讲，设置随机是跳出局部最优解的一个解决方案。Cauchy 分布的随机序列具有两翼分布宽大，在零点波峰高于Guassian 分布但两侧下降趋势比Guassian 分布较缓的特性，比Guassian 分布的抗干扰能力更强，可以利用柯西变异来改进SOA（Cauchy variation seagull optimization algorithm，CVSOA）算法。

柯西变异计算公式为

式中：Cauchy(0，1)表示为标准Cauchy 分布函数，rand(0，1)是一个大于0 且小于1 的均匀分布随机数，p为随机变异概率。

SOA 算法迭代后期，搜索海鸥个体表现出强烈聚集性，即所有海鸥个体进攻到同一个位置不再改变，这样就削弱了海鸥算法的多样性，同时海鸥种群易陷入局部最优。因此在海鸥算法陷入局部最优时，结合柯西变异策略对海鸥位置进行扰动，从而防止海鸥算法陷入早熟收敛。柯西变异的实现步骤如下：

（1）算法陷入局部最优后，判断随机数是否小于变异概率p。

（2）对目前海鸥种群进攻最佳个体位置Pbs进行柯西变异，并保留Pbs。

（3）判断海鸥种群是否陷入局部最优，若是，循环步骤（1～3），直到海鸥算法找到全局最优或者达到终止算法迭代要求。

利用式（12）对海鸥算法中海鸥位置Pbs进行变异策略。

式中：rand 为一个大于0 且小于1 的均匀分布随机数，Pbs为当前海鸥种群最佳个体位置。

2.3 VMD 模态分解

VMD 算法具有非递归分解多分量信号的能力，并可获得多个本征模态函数（Intrinsic mode function，IMF）。该方法的目的是将输入信号分解为具有特定稀疏度的模态分量。在VMD 中，本征模态函数被认为是调频调幅信号，如式（13）所示。

2.4 CVSOA-VMD 适应度函数

根据CVSOA 算法的理念，CVSOA 需要依据某个优化准则，称为适应度函数来评判参数组合是否为最优结果。考虑VMD 在运行前需要凭经验预设分解模态个数K和二次惩戒因子α，可以利用CVSOA 来优化VMD 参数组合[α，K]，避免因人为经验设置参数导致信号过分解或者是分解后信噪比低的问题。

信号复杂程度可以用幅值谱熵值大小反映，熵值越大，信息量越多，信号系统状态越不确定。幅值谱熵值是信号傅里叶变换得到幅值谱，再结合信息熵公式得到幅值谱熵值。表达式为

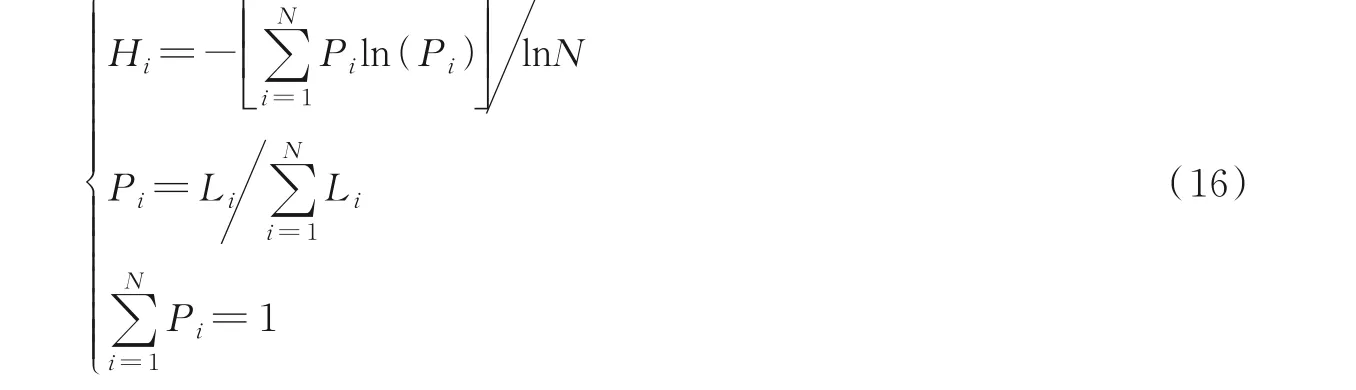
式中：Li为模态分量ui的幅值谱；Hi为模态分量ui的幅值谱熵；N为模态分量的长度。

VMD 分解后模态分量ui所对应熵值越大，表示模态分量ui内状态越紊乱，含有的噪声越多；相反，模态分量ui所对应熵值越小，表示模态分量ui内状态越稳定，含有的噪声越少。因此选用幅值谱熵值极小值为CVSOA 的适应度函数，具体实现流程如图3 所示。

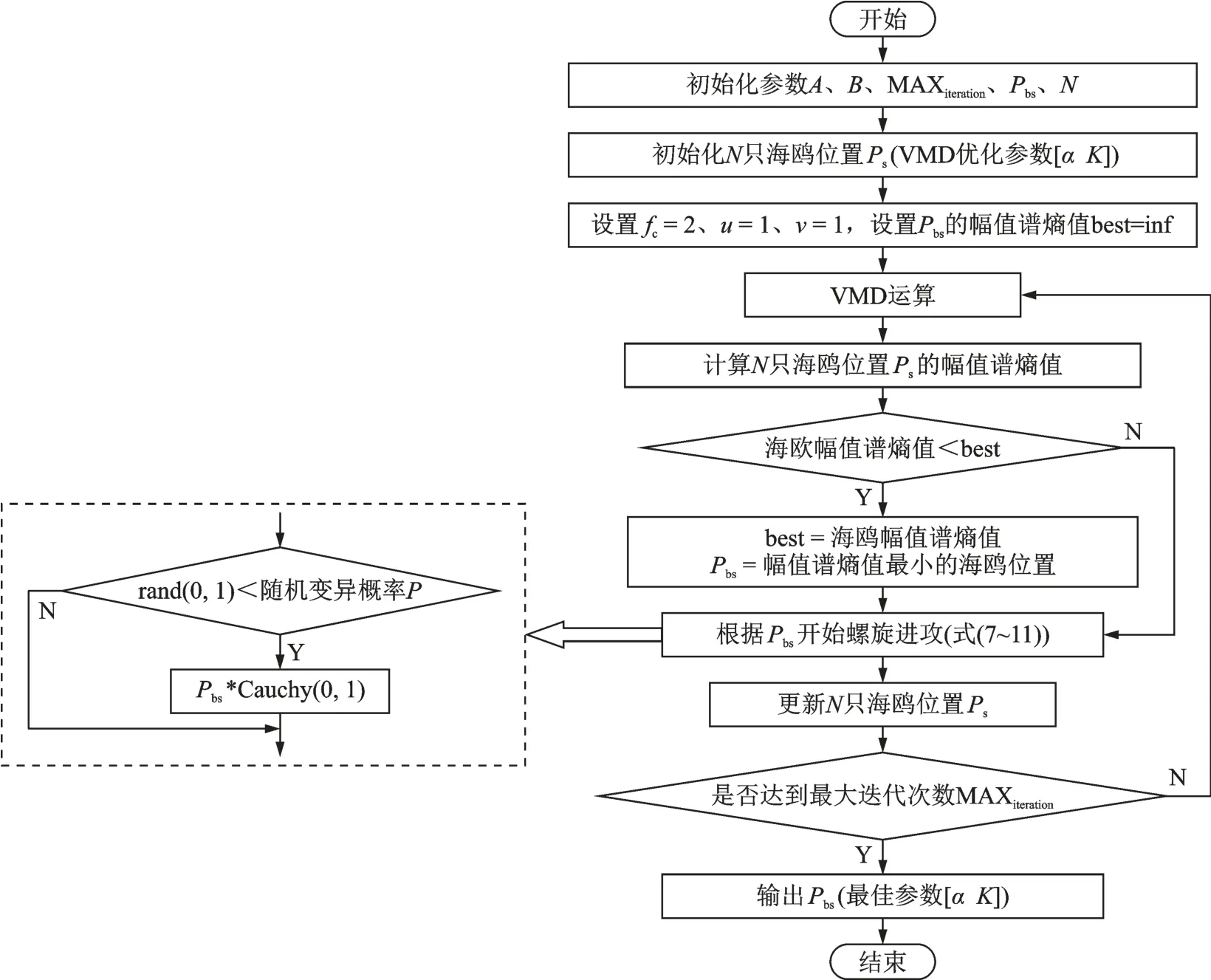
图3 CVSOA-VMD 算法流程图Fig.3 CVSOA-VMD algorithm flowchart

3 仿真验证

3.1 仿真信号设计

MAE 信号具有波动性、衰减性的特点。根据其特点建立的声发射模型为

式中：A(t)表示MAE 信号波形的幅值，θ(t)表示MAE 信号频率。MAE 信号中这两个参数通常未知，呈随机分布。利用以上模型模拟纯铁材料MAE 信号特点，并添加高斯白噪声使MAE 信号被淹没在噪声中，模拟实际采集过程中被环境噪声所影响的微弱信号。信号表达式为

该仿真信号由S1、S2两个MAE 仿真信号组成，采样点数N=8 008，t=0～0.1 ms。其中S1部分振幅大小为27 mV，频率设置为750 kHz；S2部分振幅大小为9 mV，频率设置为350 kHz。分别向信号添加信噪比为-10、-5、0、5 和10 dB 的高斯白噪声，图4 为添加-10 dB 高斯白噪声信号波形图及频谱图。

图4 MAE 仿真信号波形图和频谱图Fig.4 Waveform diagram and spectrum diagram of MAE simulation signal

MAE 仿真信号及染噪后仿真信号波形如图4（a，c）所示，其频谱如图4（b，d）所示。图4（a）观察出明显MAE 信号；而图4（c）中MAE 信号被淹没在噪声中。

3.2 仿真信号降噪

采用CVSOA-VMD 对染噪信噪比为-10 dB 的MAE 仿真信号进行分析，选取幅值谱熵值作为CVSOA 的适应度函数，利用CVSOA 对VMD 的惩罚因子α和模态分解个数K值进行寻优。考虑到分解层数K设置过大而引起的过分解现象，设定K值运算最大值为9。图5 为两种方法全局最优幅值谱熵值随海鸥种群进化迭代数变化的对比曲线。

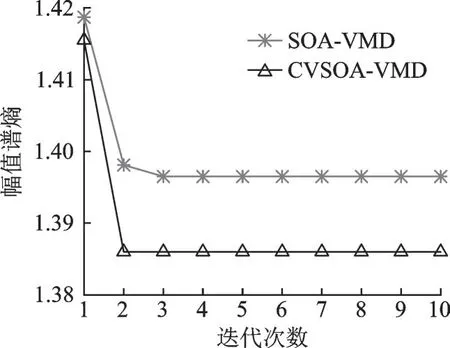
图5 迭代次数与幅值熵谱关系图Fig.5 Relationship between the number of iterations and the amplitude entropy spectrum

可以看到CVSOA 算法优化VMD 在第3 次收敛，搜索到的全局最优幅值谱熵值为1.374，最佳参数组合为［8 750，6］。然后对仿真信号使用最佳参数组合进行VMD 处理，得到如图6（a，b）所示6 个IMF 分量时域波形及频谱图，图6（c，d）为IMF 分量重构后的波形及频谱图。通过仿真结果可以观察到波形中波峰突出，尾部噪声已被有效滤去。

3.3 不同优化算法的降噪性能对比

为凸显改进SOA 算法的优越性，用基于传统SOA-VMD 参数优化方法与改进方法对比，并将信噪比SNR 和均方误差MSE 作为去噪性能评判指标，结果如表1 所示，其中D为迭代次数。

图6（e ，f）为MAE 信号在加入-10 dB 的高斯白噪声时，使用SOA-VMD 方法去噪结果。与图6（c ，d）比较，CVSOA 方法相较于传统SOA 算法，MAE 信号尾部噪声和波形毛刺均被较好滤去，去噪后的MAE 信号波形尾部更加平滑。从表1 中可得，染噪-10 dB 的MAE 信号经CVSOA-VMD 方法去噪，比传统SOA-VMD 方法的SNR 值高出1.782 1 dB，MSE 值降低0.248 9；染噪-5 dB 的MAE 信号经两种方法相比，CVSOA-VMD 方法比传统SOA-VMD 方法的SNR 值高出1.850 1 dB，MSE 值降低0.175 5。结合图5 迭代次数与幅值熵谱关系图，说明在上述情况下，传统SOA 算法陷入了局部最优，证明了SOA 算法结合柯西变异算子的优越性。在处理染噪0 dB 的MAE 信号后，两种方法的SNR 值和MSE 值接近，但CVSOA-VMD 寻优所需迭代次数更少，时间更短。

表1 仿真信号去噪效果比较Table 1 Comparison of denoising effects of simulated signals

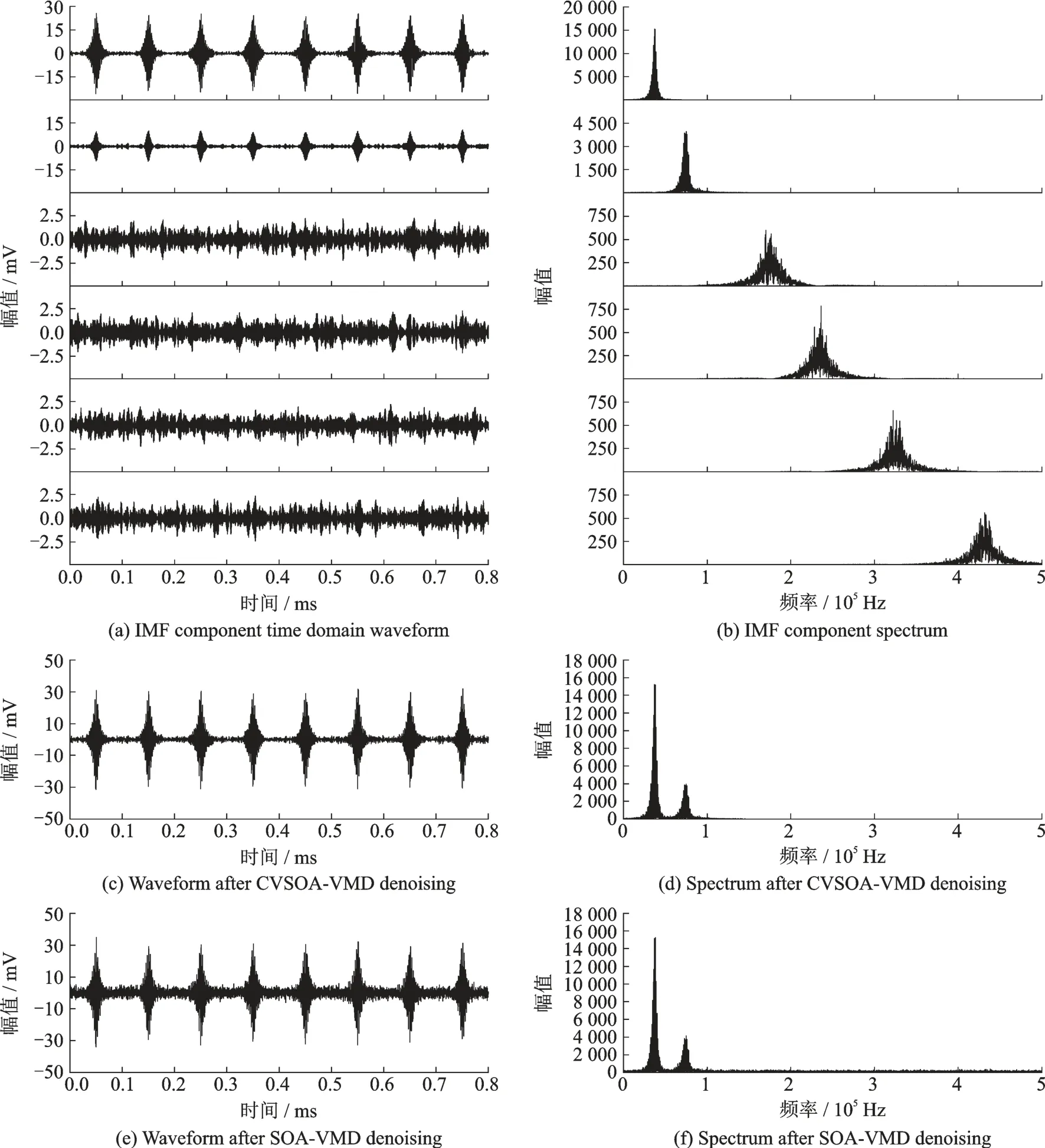
图6 仿真信号去噪后结果Fig.6 Simulation signal denoising results

分析表1 所得结果可知：处理信噪比为5 dB 的MAE 仿真信号，两种算法得出的结果相同，而对于信噪比较低的MAE 仿真信号，CVSOA-VMD 算法相较于传统SOA-VMD 算法，全局搜索能力更强，寻优所需迭代次数更少，背景噪声去除效果更佳（SNR 值显著增大，MSE 值明显减小）。

4 实验结果与分析

4.1 典型MAE 信号CVSOA-VMD 降噪

对实际采集的MAE 信号利用CVSOA 算法对VMD 预设参数寻优，并利用最优参数进行VMD 去噪，结果如图7（a，c）所示。图7（a）为处理后的各个IMF 分量的幅值谱熵值，其中IMF（1～3）的幅值谱熵值为［0.774 1，0.812 2，0.794］远远小于其他IMF 分量，说明IMF（1～3）有效信号占比高，其他IMF 分量混乱程度大，可以认定为噪声。重构后的波形及包络线如图7（c）所示，可以看出底噪明显抑制，且包络线振荡大大减少，尾部曲线平滑，证明滤除噪声的同时保留了信号细节和波动趋势。

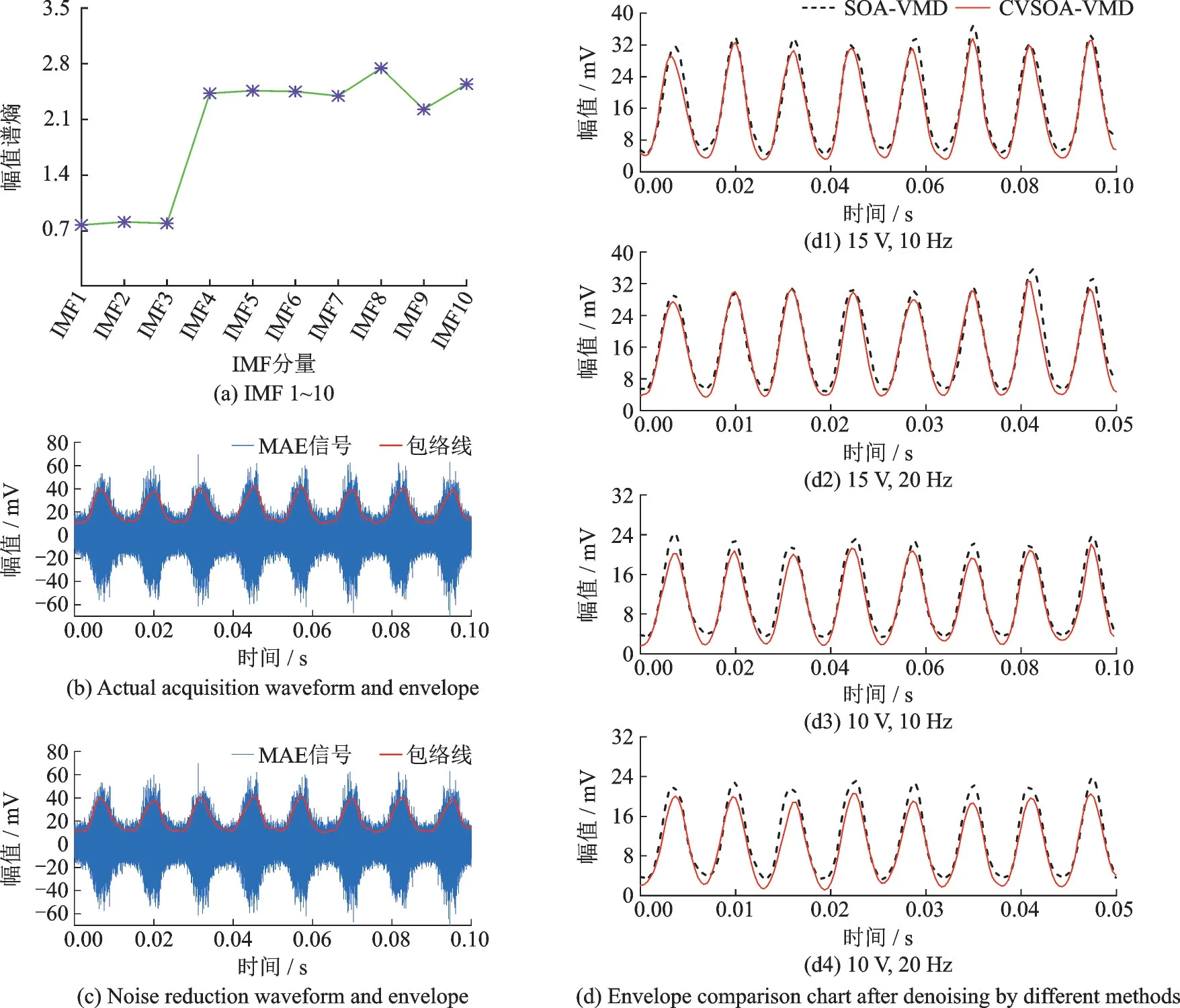
图7 实验信号分析Fig.7 Experimental signal analysis

为进一步对比去噪效果，再分别施加电压峰峰值为15 V 和10 V、频率为10 Hz 和20 Hz 的正弦激励信号，降噪后波形幅值谱熵值见表2，将不同方法得出的降噪波形绘制包络线，得到图7（d）所示的对比图。结合图7（d）和表2，CVSOA-VMD 方法去噪后信号幅值谱熵值更小，包络线动态界限清晰，尾部细节特征明显，去噪效果好。

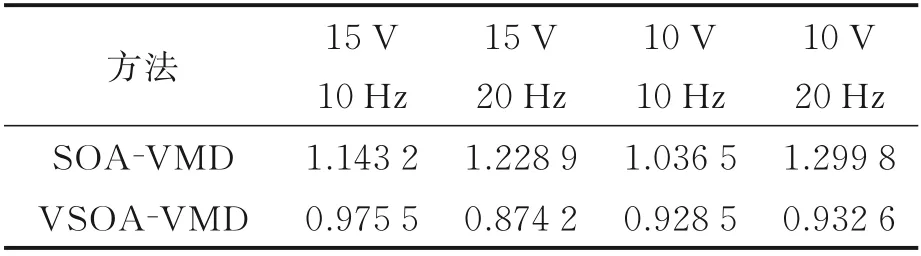
表2 不同激励信号下去噪信号幅值谱熵值对比Table 2 Comparison of amplitude spectrum entropy values of denoising signal of different excitation signals

4.2 降噪算法对磁声发射应力检测的影响

为了说明降噪算法对MAE 信号应力检测特征参数的影响，评价指标选用信号均方根（Root mean square，RMS）、包络线的偏斜度（Sk）对MAE 信号降噪结果进行分析。RMS 可以表征信号能量的大小［18］，RMS 值越大，信号能量越大，Sk则反映了信号分布偏离标准分布的程度，如果偏斜度值接近0，则信号数据相对标准正态分布是对称的，反之数据偏斜［19］。

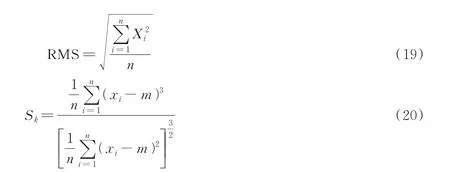
式中：xi表示第i个幅值，n表示采样数量，m表示MAE 信号幅值的平均值。

在图1 磁声发射信号采集系统基础上，分别对纯铁材料施加0、20、40、60 和80 MPa 静载拉应力，各采集6 次MAE 信号，通过CVSOA-VMD 算法降噪后对比降噪前后RMS、Sk特征值对应力变化的影响，评价指标结果如图8 所示。

图8 降噪前后特征值对应力变化影响Fig.8 Influence of eigenvalues on stress change before and after noise reduction

从图8（a）可知，由于降噪后信号能量减小，RMS 值有所降低，但其随应力变化的趋势相同，且不同应力状态下重复采集纯铁MAE 信号的RMS 值标准差减少，RMS 值的重复性更好，证明了降噪后用RMS 评估应力的鲁棒性和可靠性提高。从图8（b）可知，降噪前MAE 信号包络线Sk值集中分布在0.48～0.79 之间，降噪后MAE 信号包络线Sk值集中分布在0.27～0.36 之间，说明噪声影响了数据的真实性，降噪后MAE 信号包络线更接近于标准对称分布，在机器学习中，数据偏斜可能影响机器学习预测能力［20］，且降噪后Sk值标准差更小，可靠性更高。

5 结束语

本文提出了基于改进海鸥算法结合变分模态分解的MAE 信号去噪方法，在算法迭代过程中添加柯西变异算子持续扰动，变换搜索区域，防止算法陷入局部最优。通过仿真信号和实验信号测试，信号处理后信噪比值和均方误差明显优于传统海鸥算法结合变分模态分解信号处理方法，包络线尾部细节更清晰，去噪效果更优，且对于实验信号，去噪后降低了信号均方根和包络线偏斜度误差，提高了后续机器学习的可靠性，为消除随机噪声信号提供了一种新的思路。