距离幂次反比法(IDW)资源储量估算流程改进及应用

陈伟康，高帮飞，张书琛，姚 刚，孟 伟

(1.中铁资源集团有限公司，北京 100039；2.MKM矿业股份有限公司，科卢韦齐 20043)

资源储量估算总在特定的估算域(estimated domain)内进行，其核心问题是确定哪些已知样品点数据参与估值以及相应的权重。传统资源储量估算，一般依据规范指定的工业指标圈定矿体(品位域)，且仅利用矿体内的数据进行估值，其主要问题在于：一方面，人为分割了地质和矿化的空间分布，使得“圈矿”工作更多地关注品位，而忽略影响矿化分布的地质规律；另一方面，仅用工业品位域内的数据进行估值，往往会增强高品位数据的连续性，使得整个矿床的平均品位高估，给后期矿山开发带来风险[1]。近20年来，随着三维矿业软件在国内的普及和应用，距离幂次反比(inversed distance weighting，IDW)和克里格等估值方法不断引入，尤其是IDW方法操作相对简单，对空间数据构型(configuration)没有特殊要求，因而广泛应用于资源储量估算[2-3]。前人对IDW估值的改进主要集中在算法优化上，如参估样品数据的自动优化[4]、品位估计公式中参数确定的遗传算法[5]、通过计算权重合集的分维数来确定幂次指数[6]等。而对综合利用现有软件和技术，通过流程改进来实现估值优化却鲜有报道[7]。本文以刚果(金)Kalumbwe铜钴矿床为例，基于三维矿业软件平台，探讨如何利用分形分析和边界分析方法来确定资源储量估算的矿化域，同时引入变异函数分析辅助确定影响IDW估值的距离和幂次参数，以期通过IDW估值流程优化，提高资源储量估算的准确度，降低后期矿山开发风险。

1 IDW估值原理及流程

1.1 IDW估值原理及现行估值流程

IDW是一个局部估值工具。未知块的插值是以未知块为中心的三维搜索椭球内所有样品点的加权平均值，已知样品点的权重为距未知矿块中心点距离幂次的倒数，计算见式(1)。

i=1,2,…,n

(1)

式中：Z(x)*为未知块的估计值；z(xi)为搜索椭球内的第i个样品值；w(xi)为对应样品权重；di为样品点到未知块中心点欧氏距离；p为幂次。IDW估值原理及现行估值流程详见图1。

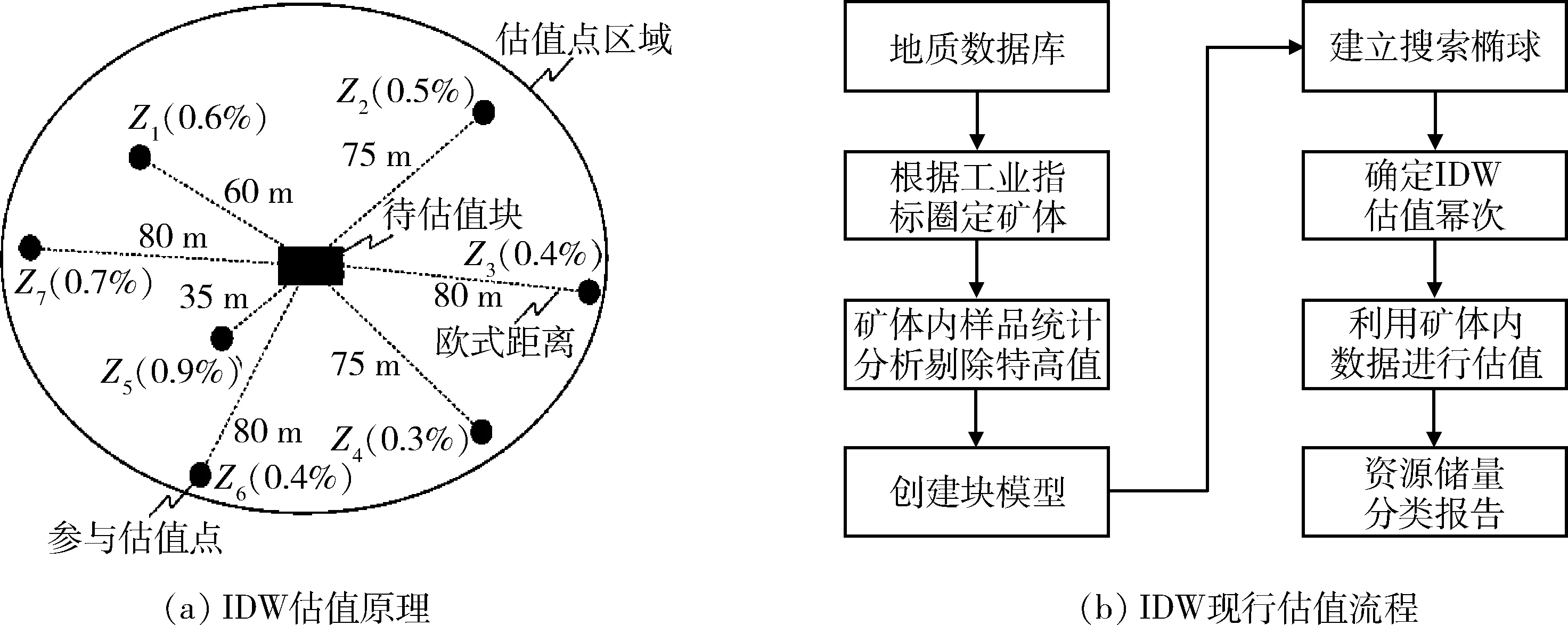
图1 IDW估值原理及现行估值流程Fig.1 Principles and current processes of the IDW estimation method

1.2 存在问题及改进思路

现行IDW估值流程的主要问题包括：①参与资源储量估算的样品集为根据工业指标圈定矿体内的所有数据，这一做法人为割裂了区域化变量在地质和统计上的连续性；②矿体的品位域在工业品位和特高值之间，估值时容易增强工业品位数据的连续性，导致估值结果偏高；③影响IDW估值的距离(与椭球半径有关)和幂次的确定主要依赖于地质工程师的认识水平，缺少量化。

本文针对上述问题，提出一种改进的IDW估值工作流程。具体思路和步骤如下所述。①引入“矿化品位域”的概念，域内数据要具有地质和统计意义上的一致性，进一步通过分形分析给出矿化品位域的范围，进而采用边界分析对工业品位域和矿化品位域的边界条件进行确认；②抓住用哪些数据参与估值及其权重分配的中心问题，主要通过变异函数的井向变异函数和全向变异函数分析提供的块金效应和最优变程信息，对IDW估值的距离和幂次参数进行约束；③所有的应用均基于现有通用三维矿业软件平台，改进的内容通用软件(三维矿业软件+Excel)可以实现，不存在技术难度，且技术的可重复性强。

1.3 矿化品位域的确定

资源储量的估算域，既可以是以岩性来划分的地质域，也可以是以品位来圈定的品位域。国内通行的做法是圈定品位域用于后续估值流程[8-11]。为了保持品位域内样品数据在地质和统计上的一致性，应剔除特异值的影响。特异值既包括特高值，也包括特低值[12]。传统做法是基于规范推荐或经设计院论证后的边界品位，作为特低品位的阈值，高于该边界品位的才会被圈入矿体。而特高值确定的方法比较多，如m+3σ法，变异系数法，直方图、CDF、概率图等[13]，统计分析一般基于矿体内数据。这些方法存在的问题是：统计分析结果受研究尺度影响；数据分组等人为因素干扰；主要针对特高值处理，不能给出特低值。采用分形方法可以有效解决这一问题，具体方法原理和计算流程参见前期的研究成果[14]，本文不再赘述。

2 应用实例概况

Kalumbwe矿床位于刚果(金)铜钴成矿带西段，为典型的沉积层状铜钴矿床[15]。矿体产出受地层控制，主矿体呈EW走向，倾向南，倾角60°～80°；主矿体长约1 km，厚度30～50 m(图2(a))，矿床由上部氧化矿体和下部硫化矿体组成。勘查阶段主要为钻孔控制，生产阶段采用钻孔+槽探进行联合控制。基本采样间距2 m，样品总数4 768件。刚果(金)政府推荐使用的圈矿工业指标为铜1.0%，钴0.1%；矿体最小可采厚度和夹石剔除厚度均为2 m。为了便于比较，利用矿化品位也进行了矿体圈连(图2(b))。

图2 刚果(金)Kalumbwe铜钴矿床钻孔分布及典型剖面Fig.2 Distribution of boreholes and typical sections of the Kalumbwe Cu-Co Deposit,D R Congo

3 分形分析与矿化品位域的确定

Kalumbwe矿床所有样品数据(Cu=0.01%，为分析下限值)和工业矿体内数据(按Cu=1.0%圈矿，未剔除夹石)的直方图、概率图以及分形统计结果如图3所示。由图3可知，直方图和概率图只能给出特高值，无法给出特低值的信息(图3(a)～图3(d))。直方图显示的特高值与统计数据范围有关，断点处分别为12%和13%(图3(a)和图3(b))。概率图则存在多个拐点12.05%、14.09%和17.04%，需通过经验判断哪个为特高值(图3(c)和图3(d))。用分形方法计算结果比较稳定，特低值为0.3%，特高值为13.9%，分形区间为0.3%～13.9%(图3(e)和图3(f))。这一区间，即为去掉特异值后的“矿化品位域”。

图3 样品数据的统计和分形分布特征Fig.3 Statistical and fractal distribution characteristics of the sample data

不同于传统方法确定矿体的品位域在工业品位和特高值之间(即所谓的“矿体”或工业品位域)，分形方法确定的是矿化品位域，域内品位变化于矿化品位与特高值之间。如果采用矿化品位域作为最终的估算域，那么部分低于工业品位的数据也将参与资源储量估算，这取决于工业品位域的边界条件。

[7] Leo Suryadinata, “Indonesian Chinese Education: Past and Present”, Indonesia, Vol. 14, No. 34 (1972), p. 70.

4 边界分析与估算域的确定

边界分析目的是通过域的边界条件分析，确定用哪些数据进行估值，形成最终的估算域。其方法是考察特定域边界两侧一定距离内品位数据的变化[11]。“硬”边界(hard boundary)即域内外的品位数据是一个突变降低的过程，说明域内外品位连续性较差，估值时仅采用域内的数据。“软”边界(soft boundary)即域内外的品位数据是一个逐步降低的过程，说明域内外品位连续性较好，估值时应采用域外一定范围内数据。“半软”边界(semi-soft boundary)则位于二者之间，一般也采用边界外一定距离内的数据参与估值。

本文重点分析矿化品位(边界品位Cu=0.3%，WF=0.3%)和工业指标(边界品位Cu=1.0%，WF=1.0%)圈定品位域的边界条件。WF=0.3%时，域内、域外在靠近边界时分别呈下降和上升趋势(图4(a)；WF=1.0%时，也有类似特征(图4(c))，两者均为“半软”边界条件。不失一般性，工业品位域为软边界或半软边界条件时，应采用矿化域数据或边界外一定范围内数据进行估值。本文采用WF=0.3%内数据参与后续变异函数分析和估值流程。

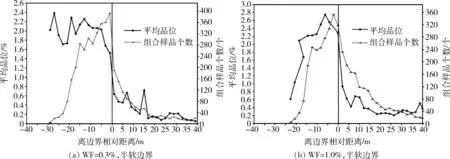
图4 矿化品位域和工业品位域的边界分析Fig.4 Boundary analysis for the mineralization and industrial grade domains

5 变异函数分析与估值参数的确定

根据IDW估值原理，进行资源储量估算前需要确定两个关键参数，即幂次和椭球搜索半径。根据经验，椭球初始搜索半径按照探明工程间距的1.25倍[16]，而幂次通常主要参考估值域的品位变化系数[17]。变异函数是描述区域化变化空间变异性的工具。研究表明，可以根据变异函数分析中块金效应的大小，来确定IDW幂次取值和椭球搜索半径相对大小[18]。一般地，块金效应越小，采用的估值幂次越高，椭球搜索半径越接近变程。本文通过变异函数的井向变异函数和全向变异函数分析提供的块金效应和变程信息，对IDW估值的距离和幂次参数进行约束。

Kalumbwe矿床矿化品位域(WF=0.3%)内铜品位数据的变异函数分析结果如图5所示。由图5可知，其块金值为0.35%2，基台值为3.52%2，计算得到块金效应为9.07%(图5(a))；全向变异函数拟合的变程为a=59 m(图5(b))。由于变异函数分析显示出低块金效应(<25%)，在后续估值流程中应采用相对高的幂次(4～5次)，椭球搜索半径尽量选择与变程一致(60 m)。

图5 矿化域内铜品位数据的井向与全向变异函数特征Fig.5 The characteristics of downhole directional and omnidirectional variogram of copper grade in the mineralized domain

6 IDW估值结果

基于工业指标(边界Cu=1.0%)圈定的线框(WF=1.0%)，用矿化品位域数据(边界品位Cu=0.3%，WF=0.3%)进行估值，考虑取2～5不同幂次的情况，结果如图6所示。由图6可知，剖面上矿化整体呈上下部强、中部弱的特征，矿化连续性方向与矿体产状基本一致，表明三维椭球参数选择适宜。从估值结果看，随着幂次的增加，矿化的结构性增强，也就是高品位和低品位矿化的连续性都得到强化。从剖面中部夹石(Cu≤0.3%)的局部验证情况明显看出，高幂次(4～5次)时，估值的夹石范围与原始钻孔数据的夹石范围基本一致；而低幂次(2～3次)时，估值的夹石范围明显较实际钻孔数据范围偏小。

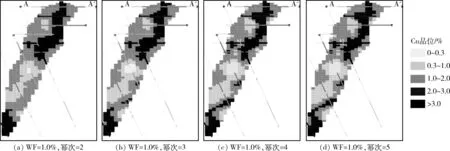
图6 不同幂次条件下矿块模型Fig.6 Block models under different power conditions

7 讨 论

7.1 工业品位域及其边界条件对估值影响

前已述及，资源储量估算首先要解决的是用哪些数据参与估值。从估值流程来看，是分2个层次或者尺度来实现的，即：①整个矿体范围内哪些数据可以用于估值(即估算域)；②对特定待估值块，具体用哪些局部数据进行估值(即搜索椭球范围)。考虑到矿山设计和开发，都需要利用一个具有经济性的矿体而不是矿化来进行，本文的讨论均以工业品位域为对象。

由图7可知，若工业品位域为硬边界条件，仅采用工业品位域内数据进行估值；但如果是软边界，应当适当扩大估算域范围，而采用矿化品位域内数据。估算域的范围将直接影响后续搜索椭球内样品点的确认。尽管未知块中心点均位于工业品位域内，但搜索椭球仍可以根据给定的参与估值数据(或者边界条件)，来确定哪些数据点参与其最终的估值(图8)。

图7 硬边界及软边界的剖面品位变化Fig.7 Section grade variation of hard and soft boundaries

1-圆从大到小依次代表工业品位域、矿化品位域和低于矿化品位样品点；2-参与估值样品点；3-待估值块；4-搜索椭球图8 不同边界条件对估值影响Fig.8 Impact of different boundary conditions on estimation(资料来源：据高帮飞[13]修改)

图9呈现了Kalumbwe矿床WF=1.0%时，在不同边界条件下，IDW估值结果与实际生产数据的对比结果。由图9可知，软边界情况下，估值结果与生产数据整体趋势吻合；但硬边界情况下，不仅估值结果差距较大，趋势也与生产数据有较大差异。这一结果与上文讨论的，本矿床工业品位域边界条件为“半软”边界的结论是一致的。此外，还可以明显看出，采用硬边界条件，估算品位比实际生产数据整体偏高。因而，不论在前期矿业项目投资收购，还是在后期设计开发阶段，都会带来隐性的经营管理风险。

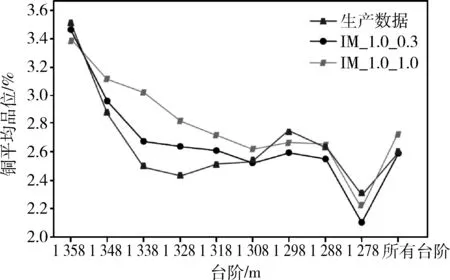
图9 不同边界条件估值结果与实际对比分析Fig.9 Comparison and analysis of different boundary conditions

7.2 块金效应与幂次的确定

为了进一步评价Kalumbwe矿床不同幂次条件下的估值效果，将估值结果与矿山实际生产数据进行对比(图10)。可以看出，低幂次条件下(2～3次)，品位总体被低估；而高幂次(4～5次)，品位总体与生产数据接近，分别计算不同幂次条件下的估计方差，见式(2)。

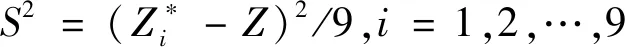
(2)

表1 不同幂次条件下的估值方差比较Table 1 Estimation variance comparison under different power conditions

为进一步评价改进IDW估值流程估值效果，将传统IDW、改进IDW(幂次为5)、普通克里格三种估值方法估值结果与矿山实际生产数据进行对比分析估值效果，其中改进IDW(幂次为5)估值结果最优(表2)。

表2 不同估值方法估值方差比较Table 2 Comparison of valuation variances of different estimation methods

7.3 改进的IDW估值流程

综合上述，本文提出改进IDW估值流程(图11)。①建立地质数据库；②对样品数据进行统计分析；③进行分形分析，剔除特高值及特低值，确定矿化品位域；④分别圈定工业品位域线框，矿化品位域线框；⑤进行工业品位域的边界分析，确定其边界条件，硬边界条件下估算域为工业品位域，软(半软)边界条件下估值域为矿化品位域；⑥进行变异函数分析，确定估值两个重要参数幂次及椭球搜索半径；⑦进行IDW估值，估值线框选用工业矿体线框，根据工业品位域的边界条件选择那些数据参与估值，通过变程确定最优搜索半径，通过块金效应大小确定幂次；⑧输出资源储量分类报告。

图11 改进的IDW估值流程Fig.11 The improved IDW estimation workflow(注：灰色部分为本文修改内容)

8 结 论

本文以刚果(金)Kalumbwe铜钴矿床为例，进行了改进的IDW估值试验，得出以下结论和认识。

1)分形分析是一种确定资源储量估算品位域的有效方法。它在不割裂矿化连续性的基础上，同时确定特高值和特低值，且不同尺度下均能给出一致的结果。

2)通过工业品位域的边界条件分析，明确了参与估值数据与域的边界条件之间的关系，硬边界条件下全部采用工业品位域内数据参与估值，否则采用矿化域数据参与估值。

3)引入克里格估值方法中的块金效应原理作为IDW估值参数选取依据，对不同估值方法之间进行融合。改进的IDW估值流程在操作上可行，该流程不仅深化了样品数据的地质特征与矿化品位特征之间的联系，同时还可以给出接近于实际生产数据的估值结果，值得在实际工作中进一步推广使用。