政府监管下煤炭企业绿色开采策略的演化博弈

马彦敏，李恩平

(太原理工大学经济管理学院，山西 晋中 030600)

煤炭作为中国的基础能源，对于支撑国民经济的发展发挥着重要的作用，但是传统的煤炭开采方式经常会引发地表坍塌、污染周边水资源、破坏土地资源等一系列生态环境问题。目前，“2030年前碳排放达到峰值、2060年前实现碳中和”已成为我国的目标，在这一愿景下，煤炭企业应该由传统以环境为代价的开采方式转变为绿色、低碳的开采方式，以实现煤炭行业的可持续发展。绿色开采是指在煤炭的生产、销售过程中，煤炭企业始终贯彻绿色发展理念，尤其是在生产过程中企业能够主动选择执行绿色开采技术，提高开采效率[1-2]。绿色开采技术的执行需要煤炭企业进行一定的成本投入，而企业出于自身利润最大化的考虑，积极主动性会减弱。政府作为煤炭企业绿色开采的监管者，有责任通过给予补贴或实施惩罚来提高煤炭企业执行绿色开采技术的积极性[3]，促使煤炭企业走上绿色开采的路径。

政府对煤炭企业监管的过程实质上是博弈的过程，学者们运用静态博弈和动态博弈的方法分别进行了研究。在静态博弈方面，吕雁琴等[4]通过分析政府和煤炭企业在生态补偿问题上的博弈行为，为新疆煤炭资源开发生态补偿机制提出了建议；徐水太等[5]研究了矿山企业如何通过与政府博弈，最终积极主动地发展绿色循环经济。在动态博弈方面，马媛等[6]、张伟等[7]通过建立政府和煤炭企业的演化博弈模型，从动态的角度探讨两个群体绿色开采监管的演化稳定策略。但是多数研究都是以政府和单一的煤炭企业作为博弈主体，有关政府和两个大型煤炭企业进行三方博弈的研究较为缺乏。因此，本文通过构建煤炭企业A、煤炭企业B以及政府绿色开采监管策略的演化博弈模型，探讨三方主体在动态博弈后的稳定策略，并用MATLAB数值仿真分析促使系统达到最优策略状态的因素，进而为煤炭企业的绿色开采提出建议。

1 基本假设与模型构建

1.1 基本假设

本文的研究主体为煤炭企业A、煤炭企业B和政府。根据演化博弈理论[8]，博弈参与方都是有限理性的，需要通过不断的学习、改进来接近最优策略，而不是在最开始就找到最优策略，因此为研究煤炭企业A、煤炭企业B和政府在不同策略组合下的成本、收益以及损失，需作出如下假设。

假设1：博弈的参与者包括煤炭企业A(m)、煤炭企业B(r)、政府(t)，并且在博弈过程中三方群体都是有限理性的，即以自身利润最大化为目标。

假设2：煤炭企业A和煤炭企业B为当地的两家大型煤炭企业，它们为了完成政府下达的指标，会存在相互搭便车的行为。

假设3：煤炭企业A的行为策略空间为执行绿色开采技术和不执行绿色开采技术(简记为M,NM)；煤炭企业B的行为策略空间为执行绿色开采技术和不执行绿色开采技术(简记为R,NR)；政府的行为策略空间为监管和不监管(简记为T,NT)。

假设4：煤炭企业A执行绿色开采技术的概率为x，不执行绿色开采技术的概率为1-x；煤炭企业B执行绿色开采技术的概率y，不执行绿色开采技术的概率为1-y；政府监管的概率为z，不监管的概率为1-z。

根据上述假设，需设置相关变量(表1)。不失一般性，假设各变量均大于0。

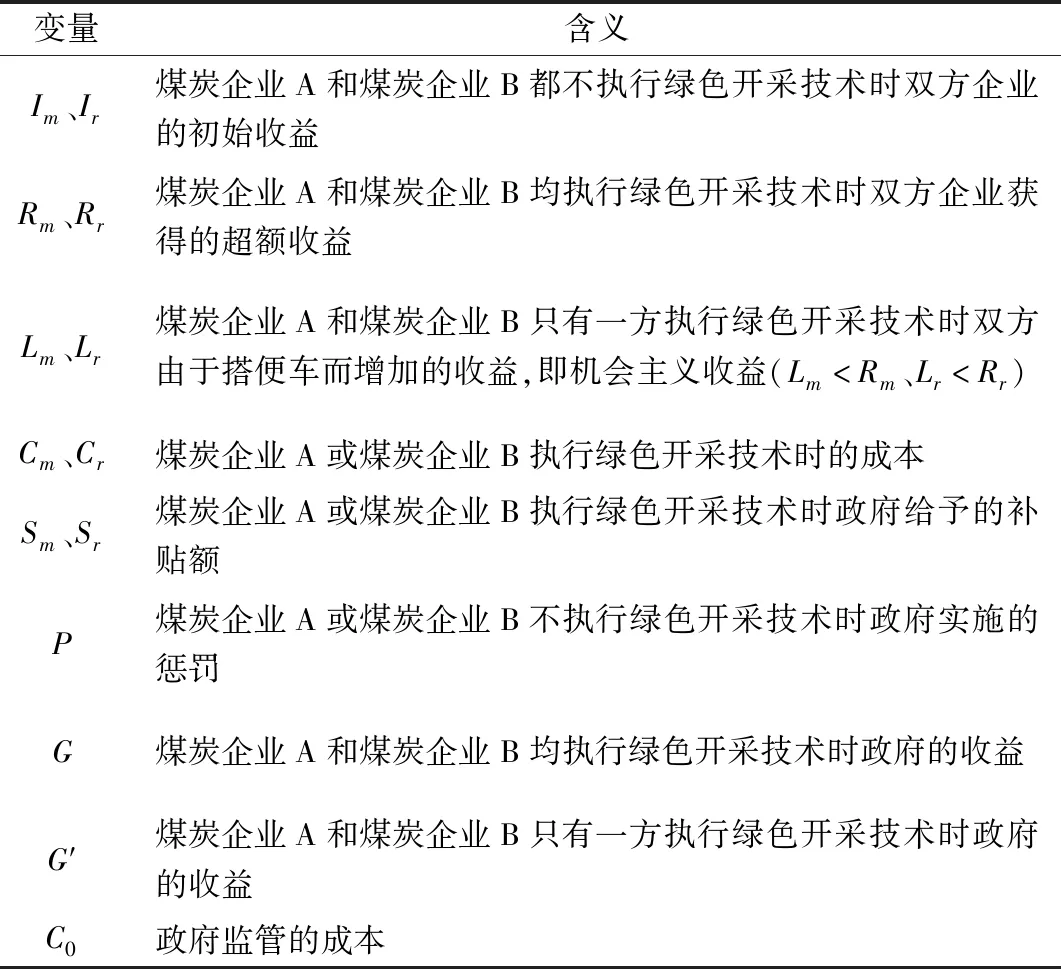
表1 变量设置Table 1 Variable settings

1.2 演化博弈模型构建

根据上述假设和变量，可以得到煤炭企业A、煤炭企业B、政府在选择不同策略时的收益矩阵，见表2。

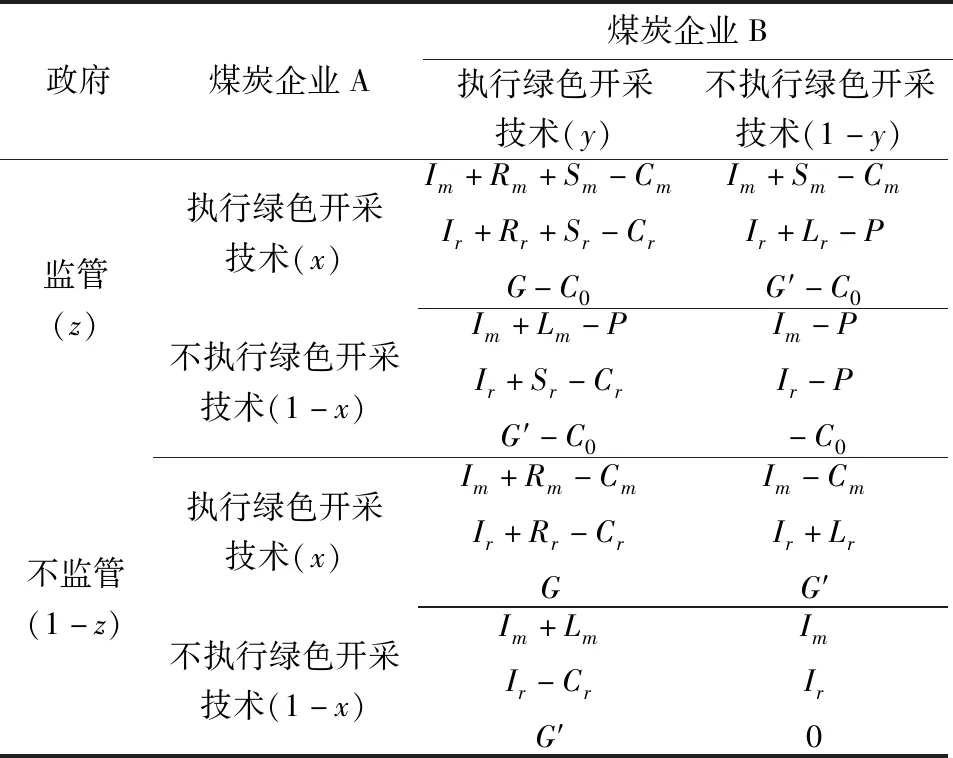
表2 煤炭企业A、煤炭企业B和政府三方博弈的收益矩阵Table 2 The income matrix of the tripartite game among coal enterprise A,coal enterprise B and the government

2 模型求解与分析

在模型构建的基础上，首先求解出煤炭企业A、煤炭企业B和政府的复制动态方程，然后通过雅可比矩阵分析三方绿色开采监管策略的演化稳定性。

2.1 演化博弈模型求解

根据表1和表2可知，煤炭企业A在博弈时执行绿色开采技术的期望收益、不执行绿色开采技术的期望收益、平均期望收益计算分别见式(1)～式(3)。

EM=zy(Im+Rm+Sm-Cm)+

z(1-y)(Im+Sm-Cm)+

(1-z)y(Im+Rm-Cm)+

(1-z)(1-y)(Im-Cm)=

yRm+zSm+Im-Cm

(1)

ENM=zy(Im+Lm-P)+

z(1-y)(Im-P)+(1-z)y(Im+Lm)+

(1-z)(1-y)Im=yLm-zP+Im

(2)

x(yRm+zSm+Im-Cm)+

(1-x)(yLm-zP+Im)

(3)

由演化博弈理论可知，煤炭企业A的复制动态方程为式(4)。

x(1-x)[y(Rm-Lm)+z(Sm+P)-Cm]

(4)

煤炭企业B在博弈时执行绿色开采技术的期望收益、不执行绿色开采技术的期望收益、平均期望收益计算分别见式(5)～式(7)。

ER=zx(Ir+Rr+Sr-Cr)+

z(1-x)(Ir+Sr-Cr)+(1-z)x(Ir+Rr-Cr)+

(1-z)(1-x)(Ir-Cr)=xRr+zSr+Ir-Cr

(5)

ENR=zx(Ir+Lr-P)+z(1-x)(Ir-P)+

(1-z)x(Ir+Lr)+(1-z)(1-x)Ir=

xLr-zP+Ir

(6)

y(xRr+zSr+Ir-Cr)+(1-y)(xLr-zP+Ir)

(7)

则煤炭企业B的复制动态方程为式(8)。

y(1-y)[x(Rr-Lr)+z(Sr+P)-Cr]

(8)

政府在博弈时监管的期望收益、不监管的期望收益、平均期望收益计算分别见式(9)～式(11)。

ET=xy(G-C0)+x(1-y)(G′-C0)+

(1-x)y(G′-C0)+(1-x)(1-y)(-C0)=

xy(G-2G′)+xG′+yG′-C0

(9)

ENT=xyG+x(1-y)G′+(1-x)yG′=

xy(G-2G′)+xG′+yG′

(10)

z[xy(G-2G′)+xG′+yG′-C0]+

(1-z)[xy(G-2G′)+xG′+yG′]

(11)

则政府的复制动态方程为式(12)。

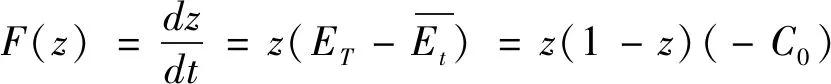
(12)

将式(4)、式(8)和式(12)联立，得到煤炭企业A、煤炭企业B、政府的复制动力系统，见式(13)。

(13)

令F(x)=F(y)=F(z)=0，可以得到局部均衡点。多群体演化博弈的演化稳定点(ESS)必然为纯策略纳什均衡，即在非对称博弈中混合策略均衡一定不是演化稳定均衡[9]。因此，后续研究仅需要分析8个纯策略均衡点，即E1(0,0,0)，E2(0,0,1)，E3(0,1,0)，E4(0,1,1)，E5(1,0,0)，E6(1,0,1)，E7(1,1,0)，E8(1,1,1)。

2.2 演化博弈模型分析

FRIEDMAN[10]提出，通过分析复制动力系统所对应雅可比矩阵的局部稳定性，可以得到该系统的演化稳定策略(ESS)，而雅可比矩阵见式(14)。

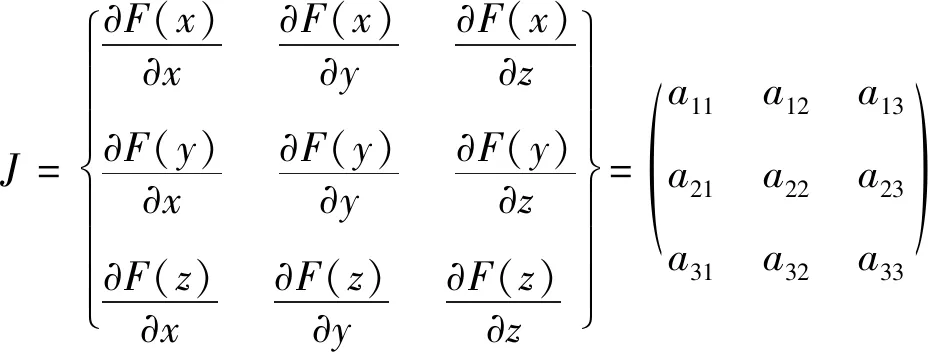
(14)

由式(13)和式(14)可知，煤炭企业A、煤炭企业B、政府复制动力系统的雅可比矩阵见式(15)。

因此，雅可比矩阵J的特征值分别为：λ1=(1-2x)[y(Rm-Lm)+z(Sm+P)-Cm]，λ2=(1-2y)[x(Rr-Lr)+z(Sr+P)-Cr]，λ3=(1-2z)(-C0)。依此类推，分别将8个纯策略均衡点代入式(15)中，可以得到各均衡点的特征值。根据李雅普诺夫判别法[11]，如果雅可比矩阵中某均衡点的所有特征值λ>0，则称该均衡点为源，即为不稳定点；如果某均衡点的所有特征值λ<0，则称该均衡点为汇，即为渐近稳定点(ESS)；如果某均衡点的特征值λ有正有负，则称该均衡点为鞍，即为不稳定点。因此分别对8个纯策略均衡点进行稳定性分析，见表3。

表3 均衡点的稳定性分析Table 3 Stability analysis of equilibrium point

根据表3，分两种情形对演化稳定策略进行讨论。

情形1：当Ri-Li>Ci(i=m,r)时，即煤炭企业A或煤炭企业B的超额收益与机会主义收益之差大于双方企业执行绿色开采技术的成本，均衡点E1(0,0,0)和E7(1,1,0)的所有特征值均小于0，即该系统有(0,0,0)和(1,1,0)两个演化稳定点，分别表示煤炭企业A和煤炭企业B均选择不执行绿色开采技术、政府选择不监管以及煤炭企业A和煤炭企业B均选择执行绿色开采技术、政府选择不监管。

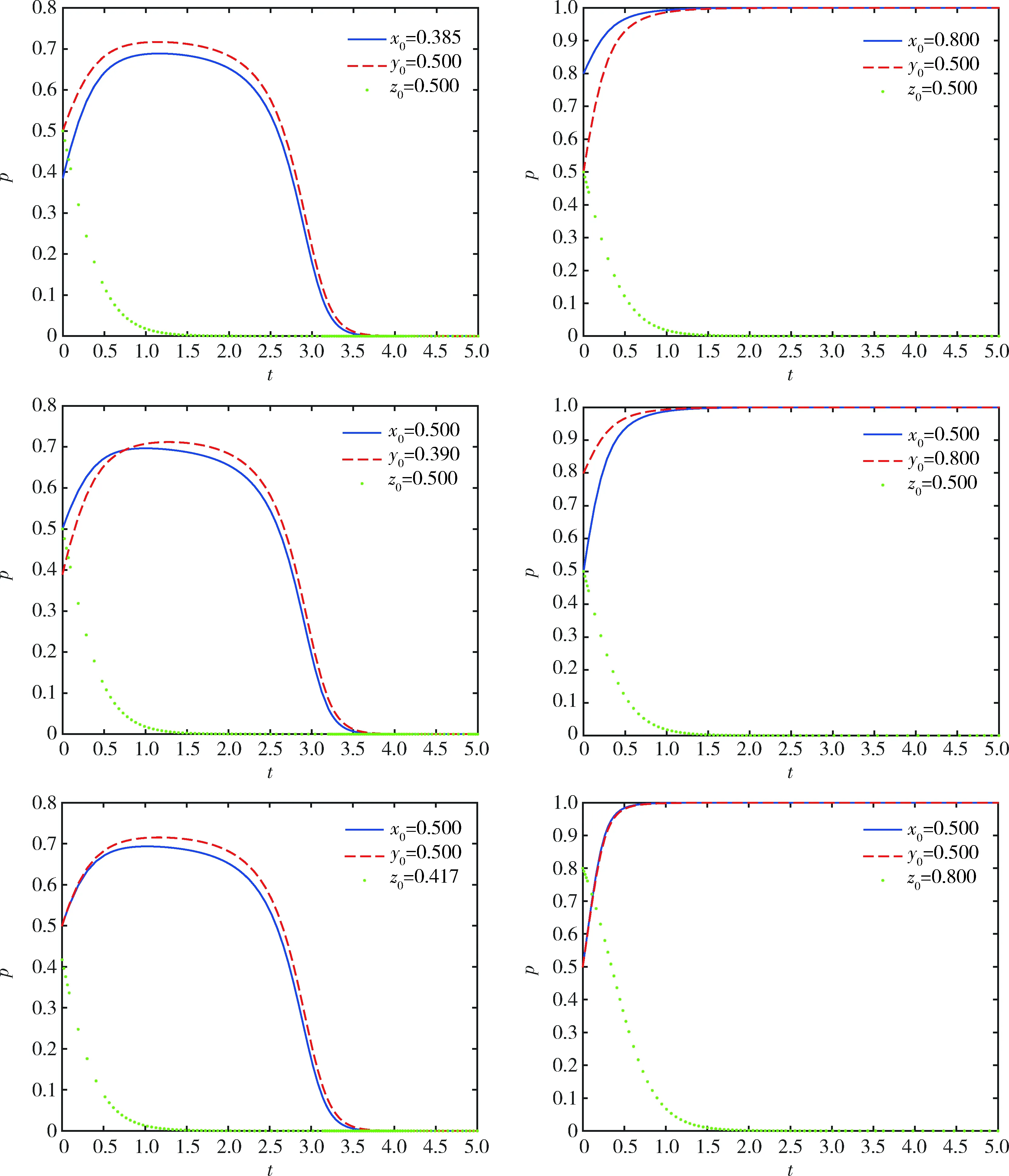
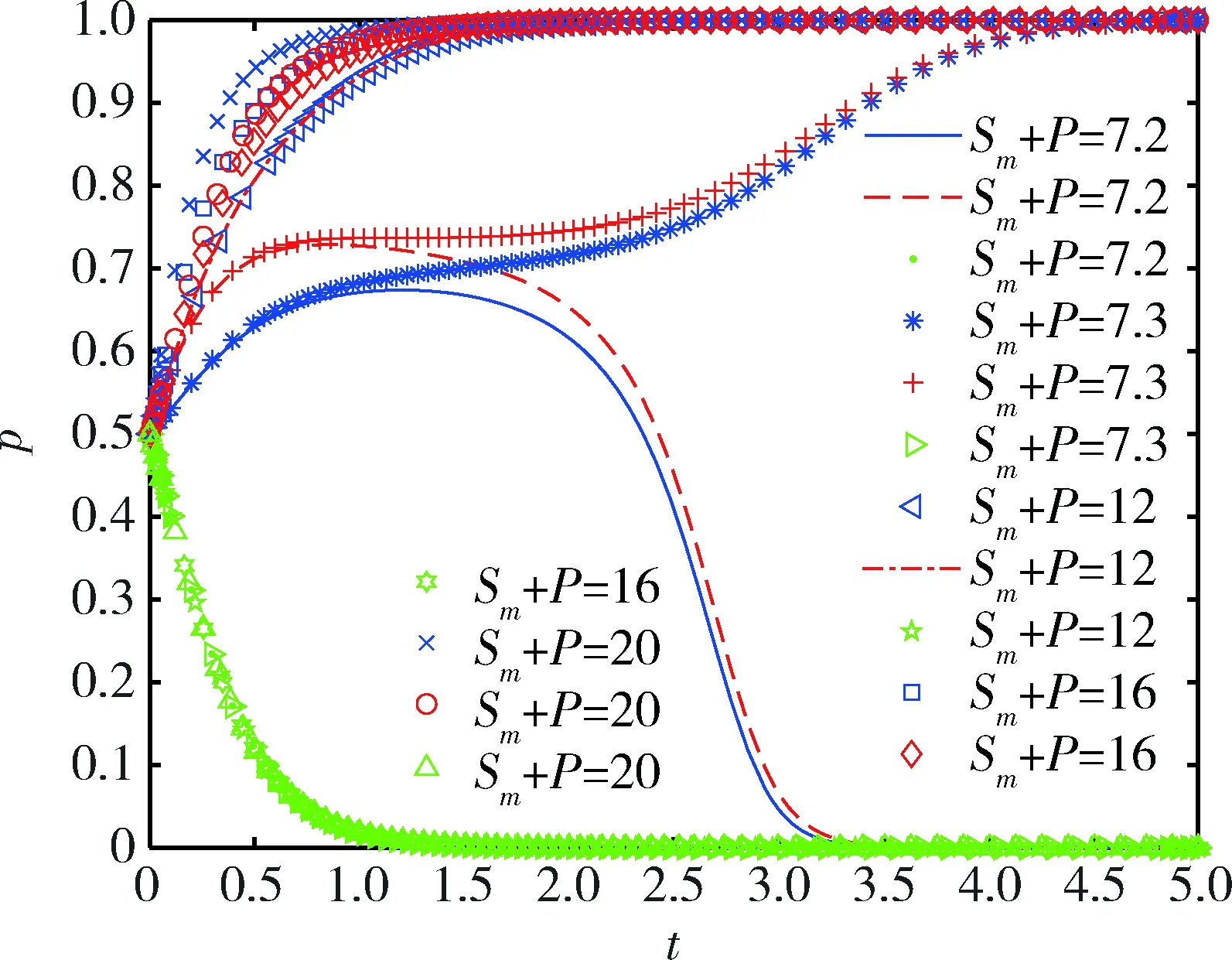
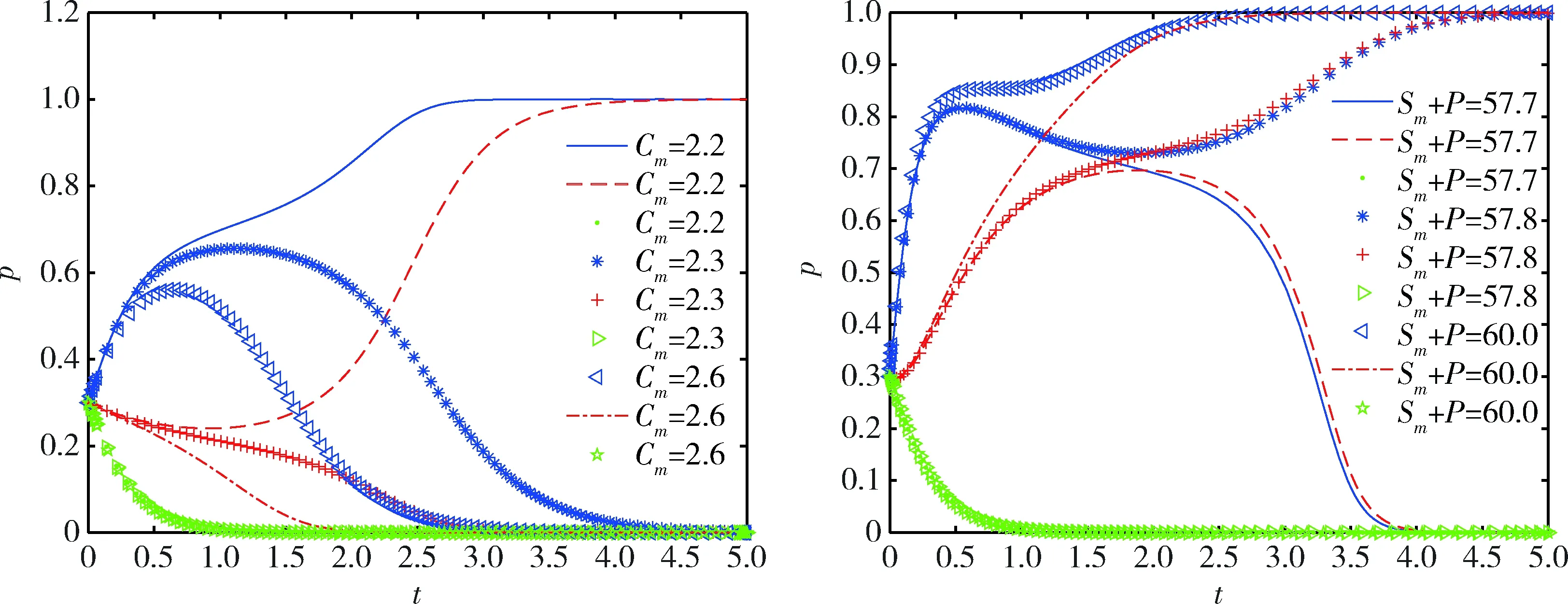
情形2：当Ri-Li

综上可知，经过一段时间的三方博弈，煤炭企业A和煤炭企业B最终的稳定策略可能是均执行绿色开采技术，也可能是均不执行绿色开采技术，而政府最终的稳定策略是不监管，即对双方是否执行绿色开采技术无作为。但是本文致力于提供煤炭企业A执行绿色开采技术、煤炭企业B执行绿色开采技术、政府不监管的发展模式，即鼓励达到(x=1,y=1,z=0)的理想策略状态，因此下文仅分析Ri-Li>Ci(i=m,r)的情形。

3 数值仿真与分析

3.1 数值仿真

为了验证当Ri-Li>Ci(i=m,r)时，煤炭企业A、煤炭企业B、政府三方的演化稳定策略以及分析相关参数对演化结果的影响，采用MATLAB2018a软件进行数值仿真及分析。本文相关参数值根据文献[12]、文献[13]和有关专家的意见设置，并且满足“Ri-Li>Ci(i=m,r)”的限制条件。因此各参数初始值的设置分别为：Rm=17，Rr=14，Lm=6，Lr=4，Cm=8，Cr=7，Sm=9，Sr=8，P=3，C0=4，t=100。在三维空间上描述不同初始点向均衡点演化的过程，演化路径如图1所示。结果表明，当煤炭企业A或煤炭企业B的超额收益与机会主义收益之差大于双方执行绿色开采技术的成本时，系统最终趋向于均衡点(0,0,0)和(1,1,0)，即该系统有两个演化稳定策略(煤炭企业A和煤炭企业B均不执行绿色开采技术、政府不监管以及煤炭企业A和煤炭企业B均执行绿色开采技术、政府不监管)，该数值仿真也符合雅可比矩阵稳定性分析的结果。

图1 不同初始点的动态演化路径Fig.1 The dynamic evolution path of different initial points

3.2 数值分析

由于本文将煤炭企业A、煤炭企业B以及政府看作一个博弈系统，而煤炭企业A和煤炭企业B在演化过程中稳定状态的形成具有相似性，因此仅对三方主体初始意愿、煤炭企业A的机会主义收益、执行绿色开采技术的成本，政府监管成本以及政府奖惩对系统演化结果的影响进行分析。

3.2.1 初始意愿对系统演化结果的影响

初始意愿对系统演化结果的影响如图2所示。从图2可以看出,当煤炭企业或政府的初始意愿较低时，系统最终趋向于均衡点(0,0,0)，即煤炭企业A和煤炭企业B均选择不执行绿色开采技术、政府选择不监管；当煤炭企业或政府的初始意愿较高时，系统最终趋向于均衡点(1,1,0)，即煤炭企业A和煤炭企业B均选择执行绿色开采技术、政府选择不监管。

图2 初始意愿对系统演化结果的影响Fig.2 The influence of initial intention on the system evolution results

3.2.2 相关参数对系统演化结果的影响

1)初始意愿均为0.5时分为两种情况，具体如下所述。

①Lm、Cm、C0对系统演化结果的影响。在初始意愿不变的前提下，分别取Lm=6,4,3、Cm=6,8,9、C0=2,4,5，演化路径如图3所示。结果表明：当Rm-Lm>Cm时，即煤炭企业A的超额收益与机会主义收益之差可以弥补其执行绿色开采技术的成本，煤炭企业A为了自身利润的最大化，最终会选择执行绿色开采技术。煤炭企业B由于和煤炭企业A在演化过程中稳定状态的形成具有相似性，最终也会选择执行绿色开采技术。由于煤炭企业A和煤炭企业B均自主执行绿色开采技术，则政府的监管概率会逐渐降低，最终会对双方企业无作为。因此，系统最终趋向于均衡点(1,1,0)，并且机会主义收益越小、执行绿色开采技术的成本越小，系统趋向于(1,1,0)的速度越快，进而越能提高煤炭企业A和煤炭企业B执行绿色开采技术的意愿。

图3 各参数对系统演化结果的影响Fig.3 The influence of various parameters on the system evolution results

当C0分别取2,4,5时，政府选择监管将产生一定的成本，此时煤炭企业A和煤炭企业B会通过更新设备等措施来避免政府的惩罚，则之后双方会趋向于自发地执行绿色开采技术，政府也趋向于不监管。因此，系统最终趋向于均衡点(1,1,0)，并且政府监管成本越小，系统趋向于(1,1,0)的速度越快，进而越能提高煤炭企业A和煤炭企业B执行绿色开采技术的意愿。

②Sm+P对系统演化结果的影响。在初始意愿不变的前提下，分别取Sm+P=7.2,7.3,12,16,20，演化路径如图4所示。结果表明：当Sm+P为7.2时，政府给予煤炭企业A的奖惩较低，由于企业群体是有限理性的，所以煤炭企业A执行绿色开采技术的意愿较低，煤炭企业B执行绿色开采技术的意愿也较低，则系统最终趋向于均衡点(0,0,0)；当Sm+P为7.3,12,16,20时，煤炭企业A和煤炭企业B执行绿色开采技术的意愿均会增加，双方之后便会趋向于自发地执行绿色开采技术，政府也趋向于不监管，则系统最终趋向于均衡点(1,1,0)。总之，随着政府奖惩取值的变化，系统会出现两个演化均衡点(0,0,0)和(1,1,0)，但是政府奖惩存在一个临界值(7.2～7.3)，当实际值大于该临界值时，系统会向(1,1,0)演化，并且实际值越大，系统趋向于(1,1,0)的速度越快，进而越能提高煤炭企业A和煤炭企业B执行绿色开采技术的意愿。

图4 政府奖惩对系统演化结果的影响Fig.4 The influence of government rewards and punishments on the system evolution results

2)初始意愿较低时。当煤炭企业A、煤炭企业B以及政府的初始意愿均较低时，经过研究发现，Cm、Sm+P有助于系统向理想状态转变，演化路径如图5所示。结果表明：Cm的取值范围为2.2～2.6，并且Cm存在一个临界值(2.2～2.3)，当实际值小于该临界值时，会使煤炭企业A、煤炭企业B由不执行绿色开采技术转变为自发地执行绿色开采技术；Sm+P的取值范围为>57.7，并且政府奖惩存在一个临界值(57.7～57.8)，当实际值大于该临界值时，会使煤炭企业A、煤炭企业B由不执行绿色开采技术转变为自发地执行绿色开采技术。

图5 Cm、Sm+P对系统演化结果的影响Fig.5 The influence of Cm and Sm+P on the system evolution results

3)初始意愿较高时。当煤炭企业A、煤炭企业B和政府的初始意愿均较高时，Lm、Cm、C0、Sm+P等参数对系统演化结果的影响小于初始意愿对系统演化结果的影响，具体如图2所示。

4 结论与建议

本文基于演化博弈理论研究了煤炭企业A、煤炭企业B和政府绿色开采监管策略的变化过程，结果表明：煤炭企业A和煤炭企业B由均不执行绿色开采技术转变为自发地执行绿色开采技术受到初始意愿、机会主义收益、执行绿色开采技术的成本、政府监管成本以及政府奖惩的影响。具体而言：当三方主体的初始意愿为中立时，机会主义收益、执行绿色开采技术成本、政府监管成本的降低会促使系统达到煤炭企业A和煤炭企业B均执行绿色开采技术、政府不监管的状态，政府奖惩在满足特定条件时会促使系统达到最优策略状态；当三方主体的初始意愿较低时，执行绿色开采技术成本、政府奖惩在满足特定条件时会促使系统达到最优策略状态；三方主体较高的初始意愿也有助于系统向理想状态演化。针对结论，本文提出如下建议。

1)有效降低煤炭企业A和煤炭企业B的机会主义收益以及执行绿色开采技术的成本。在执行绿色开采技术的过程中，煤炭企业A和煤炭企业B可能会相互搭便车，这将阻碍双方绿色开采行为的有效进行，因此，应该建立有效的沟通机制，加强双方的信任关系，降低机会主义收益；同时，煤炭企业A和煤炭企业B通过掌握关键的绿色开采技术、灵活运用绿色开采优惠政策以及加强技术人员的培训等措施来降低成本投入，促使双方企业均执行绿色开采技术。

2)降低政府的监管成本。政府监管成本过高会削弱政府的监管力度，这将直接影响煤炭企业的绿色开采行为。因此可以通过精简监管机构以使各机构之间权责分明、确保政府人员正确合理地运用经济管理权、引入第三方检查机制等措施来降低政府部门的监管成本，提升煤炭企业A和煤炭企业B执行绿色开采技术的意愿，促使双方企业均执行绿色开采技术。

3)完善政府奖惩政策。政府作为监管者，对煤炭企业A和煤炭企业B补贴、惩罚的程度会直接影响双方企业的绿色开采行为。因此，可以通过加大政府监管力度精准地进行补贴和惩罚，如政府可以根据煤炭企业执行绿色开采技术程度的不同给予差异化奖励，以使政府的奖惩政策更加完善，从而更好地引导煤炭企业A和煤炭企业B执行绿色开采技术。