李超代数的Fox导子的一些性质

茅 丹，郑克礼

(东北林业大学 理学院，哈尔滨 150040)

导子是李代数和李超代数研究中的重要对象，其中，Cartan型李代数及李超代数的导子的研究成果比较丰富[1-4]. 近年来，许多学者将李超代数的导子定义进行推广，得到了不同的广义导子[5-10]. 本文所研究的Fox导子最初是由Ralph H·Fox作为自由群环上的导子提出来的[11].

A· F·Krasnikov在文献[12]中用Fox导子的语言描述并推广了A·L·Shmelkin在文献[13]给出的结论，具体如下：设F是李代数的自由和[14]，N是F的一个理想，V是李代数使得V(N)是F的一个理想，如果V中包含F/N，则F/V(N)在V的自由代数的一种特殊运算中有忠实表示.本文又将文献[12]中关于李代数的结论推广到了李超代数，并给出了证明.

1 预备知识

设P是任意给定的基域，设F是李代数Ai(i∈I)和自由李代数G的自由和，其中：G=spanP{gj|j∈J}.F的理想N满足N∩Ai=1,(i∈I)，设U(F/N)为F/N的泛包络代数[15]，T=spanP{tk|k∈I∪J}是自由的右U(F/N)-模，设

是由

定义的同态.则kerφ=[N,N].(见文献[13])

定义1 对于u∈U(F)如果存在唯一的一组元素Dk(u)∈U(F)使得

其中：Di(u)∈AiU(F)，i∈I.则Dk(u)(k∈I∪J)称为u的Fox导子.

用Fox导子的语言描述以上结论即为，F中的元素v在[N,N]中当且仅当Fox导子Dk(v)≡0 modNU，(k∈I∪J)，其中：NU表示N生成的U(F/N)的理想.(见文献[12])

2 Fox导子的性质

本节仍然用P表示任意给定的基域.设L是李超代数，U(L)是L的泛包络代数[9]，L(k)是L的k阶交换子理想.

[u,v]=uv-(-1)d(u)d(v)vu.

若M是L的一个理想，则用MU表示M生成的U(L)的理想.如果M是由集合X生成的L的理想，则M可以写为M=idL(X).

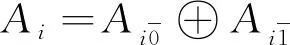
对于李超代数F的泛包络代数U(F)中的元素u，设Dk(u)(k∈I∪J)是u的Fox导子.很容易证明以下的关系式：

Dk(αu+βv)=αDk(u)+βDk(v),(k∈I∪J).

Dj(gj)=1,(j∈J),Dk(gj)=0,(k≠j)

Di(ai)=ai,(ai∈Ai,i∈I),Dk(ai)=0,(k≠i).

Dk([u,v])=Dk(u)v-(-1)d(u)d(v)Dk(v)u.

Dk([n,u])≡Dk(n)umodNU,(k∈I∪J).

其中：α,β∈P，u,v∈hg(F)，n∈N.

引理1 设K是I∪J的子集，FK是F的子代数，且

FK=spanP({Ai|i∈K∩I}{gj|j∈K∩J})

设{uk|k∈K}⊆U(FK)满足除了有限个k之外都有uk=0以及ui∈AiU(FK),∀i∈K∩I.如果

(1)

则存在v∈FK∩N，使得Dk(v)≡ukmodNU,k∈K.

(2)

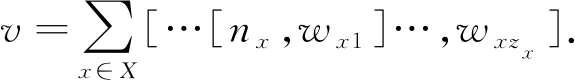
(3)

于是，

因此，

(4)

对比式(3)、(4)这两个式子可得Dk(v)≡ukmodNU,k∈K.

定理1 设K是U∪J的子集，FK是F的子代数，

FK=spanP({Ai|i∈K∩I}∪{gj|j∈K∩J}).

设{uk|k∈K}⊆U(F)满足除了有限个k之外都有uk=0以及ui∈AiU(F),∀i∈K∩I.如果

(5)

则存在v∈idF(FK∩N)，使得Dk(v)≡ukmodNU,k∈K.

证明：设U(F)有一组基是形如式(2)的单项式的集合.于是，存在一组单项式f1,…,fm，当i≠j时，fi≠fj，并且它们形如式(2)，其中：k1=…=kμ=l1=…=lυ=m1=…=mη=ξ=α=β=0，满足

(6)

其中：当k∈K∩I，ukl∈AkU(FK)，当k∈K∪J时，ukl∈U(FK).根据式(6)可得

结合式(5)有

(7)

根据式(7)和引理1，在FK∩N中存在一组元素v1,...,vm使得

Dk(vl)≡uklflmodNU,k∈K.

(8)

(9)

根据式(8)、(9)可得

(10)

根据式(6)、(10)，有Dk(v)≡ukmodNU，k∈K.定理得证.

定理2 设K是I∪J的子集，FK是F的子代数，且

FK=spanP({Ai|i∈K∩I})∪{gj|j∈K∩J}).

则

Dk(v)≡0modNU,k∈(I∪J)K,

(11)

当且仅当存在FK中的元素v0和idF(FK∩N)的元素v1使得v≡v0+v1mod[N,N].

证明：充分性是显然的，下面仅证明必要性.

设U(F)有一组基是形如式(2)的单项式的集合.由式(11)可知F中的元素v是形如式(2)的单项式的线性组合，其中：k1+…+kμ+l1+…+lυ+m1+…+mη+ξ+α+β≥1，因此，v∈FK+N.于是存在v0∈FK使得v-v0∈N.从而有

(12)

根据式(12)和定理1，存在v1∈idF(FK∩N)使得

Dk(v-v0)≡Dk(v1)modNU,k∈(I∪J).

则有Dk(v-v0-v1)≡0modNU,k∈(I∪J)，从而v≡v0+v1mod[N,N].定理得证.

定理3 设0≠r∈F，R=idF(r)满足R∩Ai=1(i∈I).设s∈I∪J，K=(I∪J){s}，FK=span({Ai|i∈K∩I}∪{gj|j∈K∩J})是F的子代数.则FK∩R=0当且仅当Ds(r)≢0modRU.

充分性用反证法，假设FK∩R≠ 0，因为FK∩R是自由的李超代数[15-16]，所以FK∩R≠[FK∩R,FK∩R].设v∈FK∩R[FK∩R,FK∩R].考虑U(FK)中的元素Dk(v)(k∈I∪J)，存在t∈K，使得Dt(v)≢0mod(FK∩R)U’，其中：(FK∩R)U’是由FK∩R生成的U(FK)的理想.因此，Dt(v)≢0modRU.另外存在β∈U(F)使得

Dk(v)≡Dk(r)βmodRU,k∈I∪J.

(13)

根据式(13)及v∈FK可得

0≡Ds(r)βmodRU.

(14)

由于超代数U(F/R)没有零因子，根据式(14)以及Ds(r)≢0modRU可知β≡0modRU.因此，Dt(v)≡0modRU，矛盾.综上，定理得证.