先行、后行盾构不同位置施工对土体变形影响研究

丁 智，冯丛烈，董毓庆，徐 涛，张默爆

(1.浙大城市学院 土木工程系，浙江 杭州 310015；2.浙江省城市盾构隧道安全建造与智能养护重点实验室，浙江 杭州 310015；3.绍兴文理学院 土木工程系，浙江 绍兴 312000；4.深圳市市政工程总公司， 广东 深圳 518109)

近年来，地铁建设作为城市地下空间开发的新标志，其发展进程不断加快，大多采用双线平行盾构施工。然而，城市高楼林立，地下管网纵横交错，建筑物桩基、市政管线、既有隧道等既有构筑物都会对新建地铁的路线及穿越形式产生较大的限制。因此，地铁建设也越来越多的呈现出双线重叠、多线重叠施工工况。但重叠施工存在较多风险隐患，尤其是在低渗透的饱和土地区，由于其压缩性大、灵敏度高等特点，土体扰动变形更为明显。因此，针对饱和土地区重叠盾构不同位置施工引起土体变形的研究有着重要的工程意义和学术价值。

目前，关于双线重叠盾构施工引起土体变形的理论研究方法较多，主要有数值模拟法[1-5]、实测分析法[6-7]、理论解析法[8-16]。典型的理论解法主要有随机介质理论[8-9]、Peck解[10-13]、Sagaseta解[14]、Mindlin解[15]、饱和土解[16]、复变函数法[17]等。国内外学者对理论解析法进行了积极的探索，但大多只针对双线平行施工，如马可栓[10]基于Peck公式，采用超几何方法推导出双线平行盾构施工引起的地表沉降。文献[11-12]在马可栓的基础上，对土体损失率和沉降槽宽度系数的计算式进行修正，建立双线平行盾构引起的二维深层土体沉降。但盾构在施工中是一个动态变化的过程，陈春来等[13-14]通过研究得出了土体损失率沿纵向上的变化，代入计算得出了双线平行盾构施工引起的三维土体总变形，但其在推导过程中仅考虑了土体损失的影响，忽略了刀盘附加推力、盾壳摩擦力、盾尾注浆压力的影响，导致最终结果与实测值有较大偏差。魏纲等[15]在其基础上考虑了盾构施工中刀盘附加推力等因素的影响，并在计算土体损失引起的地表变形时，发现先行隧道施工会导致后行隧道地表沉降最大值产生偏移，因此，修正了土体移动模型，最终提出了多因素下双线盾构施工引起地表变形的计算方法，但其仅针对土体为单相介质的工程，不能适用于饱和土双相介质的情况。丁智等[16]考虑饱和软土特性及盾构施工过程中孔压消散的影响，推导出饱和软土双线平行盾构施工引起的土体变形计算公式，但其采用的刀盘附加推力等施工参数的计算式仍存在较多不足，与实际情况偏差较大，且只考虑了双线盾构位置平行这一单一工况。

上述关于双线盾构施工对土体变形的影响大多仍处于平面上的研究，未考虑双线盾构不同位置存在的相互作用影响。张治国等[17]基于交替法和复变函数理论，采用位移控制隧道椭圆化收敛变形，得到双线隧道在不同布置方式下施工引起周围土体变形的计算方法，但其未考虑隧道开挖先后顺序的影响，也未提出先行隧道对后行隧道影响范围和影响程度界限。

针对现有研究的不足，本文基于半无限饱和土初值解，充分考虑了先行、后行盾构位置及施工间隔不同对后行隧道土体二次扰动的影响，以及施工参数计算中考虑了挤土效应、浆液漫延、土体软化、浆液自重、环向不均匀注浆压力、浆液填充盾构间隙等因素的影响，修正了现有饱和土双线盾构施工引起的土体变形计算公式，建立了先行、后行盾构任意空间位置动态施工的修正力学模型，并结合典型的伦敦饱和黏土工程案例，通过与经典的Mindlin解和丁智解[16]进行对比，从而验证了本文计算方法的正确性。

1 双线盾构土体变形修正计算公式

1.1 饱和土盾构施工引起的土体变形理论解

目前关于饱和土地区双线盾构施工引起的土体变形研究少有考虑饱和土双相介质的影响，大多采用仅考虑单相介质的Mindlin解计算，导致最终预测结果有所偏差[18]。陈振建[19]基于Biot固结控制方程[20]，根据饱和土受集中力作用下的边界限定条件，推导出半无限饱和土内部作用水平力和竖直力时土体任意位置的变形。丁智等[16]进一步采用数值积分，计算得到了双线盾构推进过程中刀盘附加推力、盾壳摩擦力以及盾尾注浆压力作用下的土体竖向变形。

本文基于笔者推导的半无限空间饱和土双线盾构施工引起土体变形的计算公式，借鉴王洪新[21]、ALONSO等[22]、张雨帆[23]和魏纲等[24]在各施工参数上的研究成果，通过修正丁智解，建立饱和土双线盾构任意空间位置动态施工的修正力学模型。

1.2 双线盾构修正前后力学模型对比

双线盾构施工过程中受力分析及位置关系见图1，图中右行线为先行线，盾构开挖面位于y=0平面，L为盾构全长，Rs为隧道半径，先行、后行盾构的施工间隔为t，隧道轴线间距为J，埋深分别为z0、z1，双线盾构掘进均沿着y轴负方向。本文提出的修正力学模型有如下特点：

考虑了先行、后行盾构位置及施工间隔不同对后行隧道土体二次扰动的影响；在原附加推力q′的基础上考虑了挤土效应的影响；在原盾壳摩擦力f′的基础上考虑了土体软化的影响以及浆液漫延导致盾尾部分摩擦力有一定的折减；在原注浆压力p′的基础上考虑浆液自重及环向不均匀分布的影响并将其分区处理。

图1 双线盾构推进受力分析示意

1.3 刀盘附加推力引起的土体变形

双线盾构刀盘附加推力引起的土体变形，积分示意图见图2。

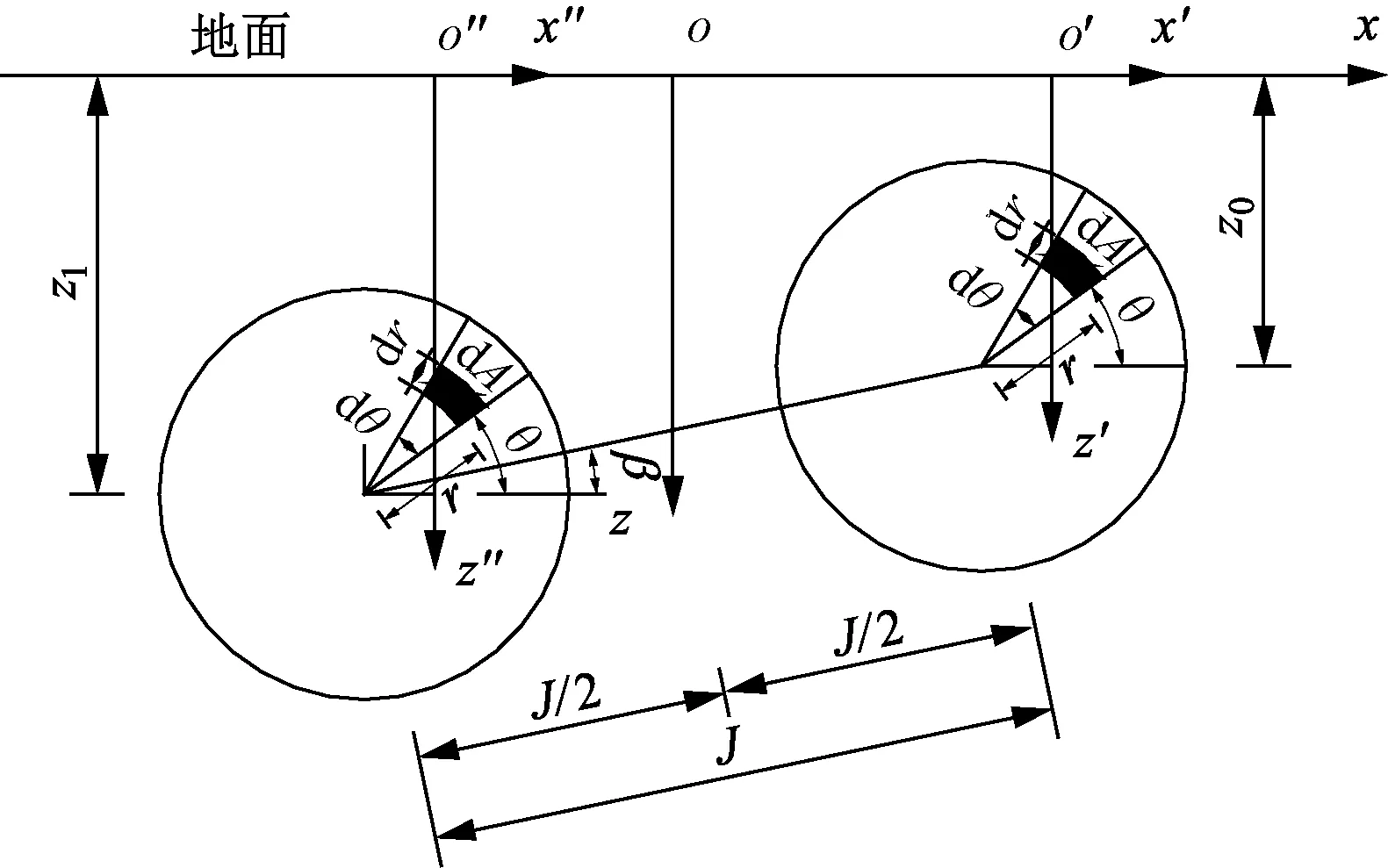
图2 刀盘附加推力积分示意

图中2中，β为隧道中心连线与水平线的夹角。经坐标转换后得到

(1)

式中：G为剪切弹性模量。

(2)

王洪新[21]在计算刀盘附加推力时，考虑了刀盘挤土效应的影响，并据此建立了刀盘挤土模型，推导出更合理的刀盘附加推力计算公式

(3)

式中：μ为泊松比，软土在不排水的条件下取μ=0.5；ν为盾构掘进速度；Δp′为刀盘切入土体产生的挤压力，一般取10～25 kPa；Eu为土体不排水弹性模量，软土地层中取Eu=(2.5～3.5)Es，Es为压缩模量，土质越硬，压缩性越小的土层其系数取值越大；w为刀盘转速；k为刀盘闭口部分幅数；D为刀盘直径；ξ为刀盘开口率。

对式(1)进行积分可得在刀盘附加推力作用下，xyz坐标系中任意点的土体竖向变形表达式为

(4)

1.4 盾壳摩擦力引起的土体变形

双线盾构盾壳摩擦力引起的土体变形，积分示意见图3。

图3 盾壳摩擦力积分示意

经坐标转换后得到

(5)

式中：

(6)

文献[25]中提到，在盾构施工过程中，浆液会漫延至距离盾尾约2.2 m，故笔者将处于漫延区的摩擦力乘折减系数λ，减小了盾壳摩擦力更符合工程实际。盾壳与周围土体的摩擦特性与桩-土界面相似，应考虑土体的软化特性。据此，本文基于Alonso等[22]推导的桩-土界面摩擦力公式，将其运用到软土区盾壳摩擦力的求解中，计算简图见图4。

图4 盾壳表面应力状态示意

(7)

式中：σθ为作用于盾壳的径向正应力，可由作用于盾壳θ位置处的竖向与水平土压力σv、σh求解得出；σ轴为盾构轴线处的竖向土压力；K0为侧向静止土压力系数；γ为土体重度；δ′为盾构与周围土体的截面摩擦角，Potyondy[26]通过界面剪切试验得到黏土与光滑钢材界面摩擦角为6.5°～9°；张忠苗等[27]通过实测得桩-土界面残余摩阻力τsr与极限侧摩阻力τsu的比值βs=0.83～0.97。

对式(5)进行积分就得在盾壳摩擦力作用下，xyz坐标系中任意点的土体竖向变形表达式为

(8)

式中：l为浆液漫延长度。

1.5 注浆压力引起的土体变形

双线盾构注浆压力引起的土体变形积分见图5。

图5 盾尾注浆压力积分示意

经坐标转换后得到

(9)

式中：

(10)

张雨帆[23]将盾尾注浆填充视为牛顿流体扩散模型，并充分考虑管片半径、盾尾空隙等因素，推导得出注浆压力沿盾尾空隙环向分布的计算公式。

(11)

式中：pi为盾尾分区注浆压力，±根据浆液填充方向判断，向上为-，向下为+；A为牛顿流体系数；q为浆液流量；μ(t)为浆液黏度系数，牛顿流体取值为0.005 Pa·s；r0为盾尾间隙的一半；α0为注浆孔与x轴的夹角。当浆液向上填充时，式中(sinα-sinα0)>0，使得-ρgRs(sinα-sinα0)<0，此时浆液重力对注浆压力产生减压效果；当浆液向下填充时，式中(sinα-sinα0)<0，使得-ρgRs(sinα-sinα0)>0，此时，浆液重力对注浆压力产生加压效果，符合工程实际。

为计算简便，本文以4孔注浆为例，注浆孔位于45°、135°直线上，将注浆区域分为4小块，见图6。左右两区域平均注浆压力相同，顶部平均注浆压力最小，底部平均注浆压力最大，若注浆孔数量及位置不同时则需对算式做进一步修改。

图6 注浆压力分布示意

对式(9)进行积分就可得到在注浆压力作用下，xyz坐标系中任意点的土体竖向变形表达式为

(12)

式中：m为单环管片宽度。

1.6 土体损失引起的土体变形

魏纲等[24]在Sagaseta的基础上综合Loganathan等[28]提出的考虑土体泊松比及椭圆非等量径向土体移动模型，对Sagaseta解进行修正，笔者在此基础上推导出任意空间位置的双线盾构土体损失引起的土体变形计算公式为

(13)

式中：b为后行隧道沉降槽偏移量；Vloss1、Vloss2分别为先行、后行隧道单位长度的土体损失量，根据Lee等[29]提出的等效土体损失概念，进一步考虑了先行隧道施工对后行隧道的影响，对隧道土体移动模型及相应的单位长度土体损失量计算式进行修正，见图7。

图7 隧道土体移动模型

目前国内外对后行隧道土体损失率的研究较少，vloss后的取值主要依赖于地区经验，对于后行隧道不同位置的土体损失率取值仍处于空白区，依据现有盾构隧道施工对土体扰动范围的研究[30-31]，建立双线盾构土体受扰动模型，见图8。模型假设：

(1)土质均匀单一，复合地层以等效重度原则进行土层厚度的转化。

(2)扰动范围内不考虑因距离隧道中心远近而导致扰动程度不同的影响。

(3)土体二次扰动部分对后行隧道的影响为均匀分布。

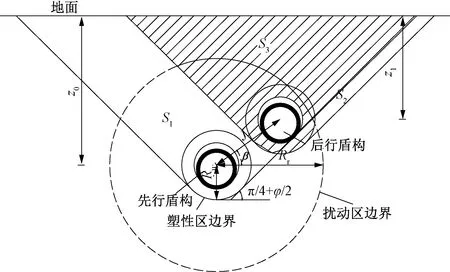
图8 双线盾构土体受扰动模型

图8中，φ为土体内摩擦角；S1为土体受先行隧道施工扰动的面积，包括距离隧道中心Rr的开挖卸载区和与塑性区边界线Ru相切水平仰角为(π/4+φ/2)的剪切扰动区；S2为地表沉降受后行隧道施工影响的土体扰动面积；S3地表沉降受先行、后行隧道施工影响的土体二次扰动面积。塑性扰动区半径取值见式(14)，具体推导过程可见黎春林等[30]的研究。

(14)

式中：σ0为初始地应力；c为土体黏聚力。

先行隧道对后行隧道的影响主要体现在土体受施工扰动后其力学指标(如承载力、压缩模量等)发生改变，导致后行隧道施工引起的土体变形更明显。本文仅考虑土体在负扰动状态下压缩模量的变化，引入扰动参量、扰动系数，推导出后行隧道土体损失率的计算式为

(15)

工程中土体损失率的实际值与设计值常因注浆量、土质、施工精度等不同而有所偏差，即使在相同地区，先行、后行隧道的土体损失率也均会出现不一致的现象。本文提出的先行、后行隧道土体损失率计算式能适用于先行、后行盾构位于任意空间位置的工况，规律分析见本文2.2节。

1.7 盾构推进引起的土体总变形

考虑了先行、后行盾构位置及施工间隔不同对后行隧道土体二次扰动的影响以及施工参数计算中考虑了挤土效应、浆液漫延、土体软化、浆液自重、环向不均匀注浆压力、浆液填充盾构间隙等因素的影响，推导出饱和土双线盾构任意空间位置动态施工引起的土体总变形计算式为

μz=μz-q+μz-f+μz-p+Szf

(16)

2 算例验证与分析

2.1 算例：伦敦海德公园盾构隧道

海德公园隧道项目位于伦敦市中心，东、西行隧道采用双线平行盾构施工，穿越典型的伦敦饱和黏土地层，详情见文献[32]。西行隧道为先行线，东行隧道为后行线，隧道轴线埋深为34.5 m，隧道间距为16.2 m，盾构机全长11 m，平均掘进速度为1.1 cm/min。刀盘直径7.1 m，开口率为33%，转速为1.1 r/min，闭口部分幅数8幅。衬砌内外径为6.2、6.8 m，单环宽1.6 m。侧向静止土压力系数为0.6，弹性模量约为10 MPa，不排水弹性模量约为30 MPa，抗剪切刚度为10.7 MPa，伦敦黏土强度较高，侧摩阻力软化系数为0.85，土体与盾壳界面摩擦角为6.5°，先行隧道土体损失率约0.75%，后行隧道土体损失率约1.7%，隧道相对位置及监测点布置见图9。

图9 海德公园隧道位置图(单位：m)

实测与计算先行、后行隧道施工引起纵向地表增量变形见图10，图10中y为盾构刀盘距监测断面的距离，Δw为地表增量变形。

图10 实测与计算先后行隧道施工引起纵向地表增量变形

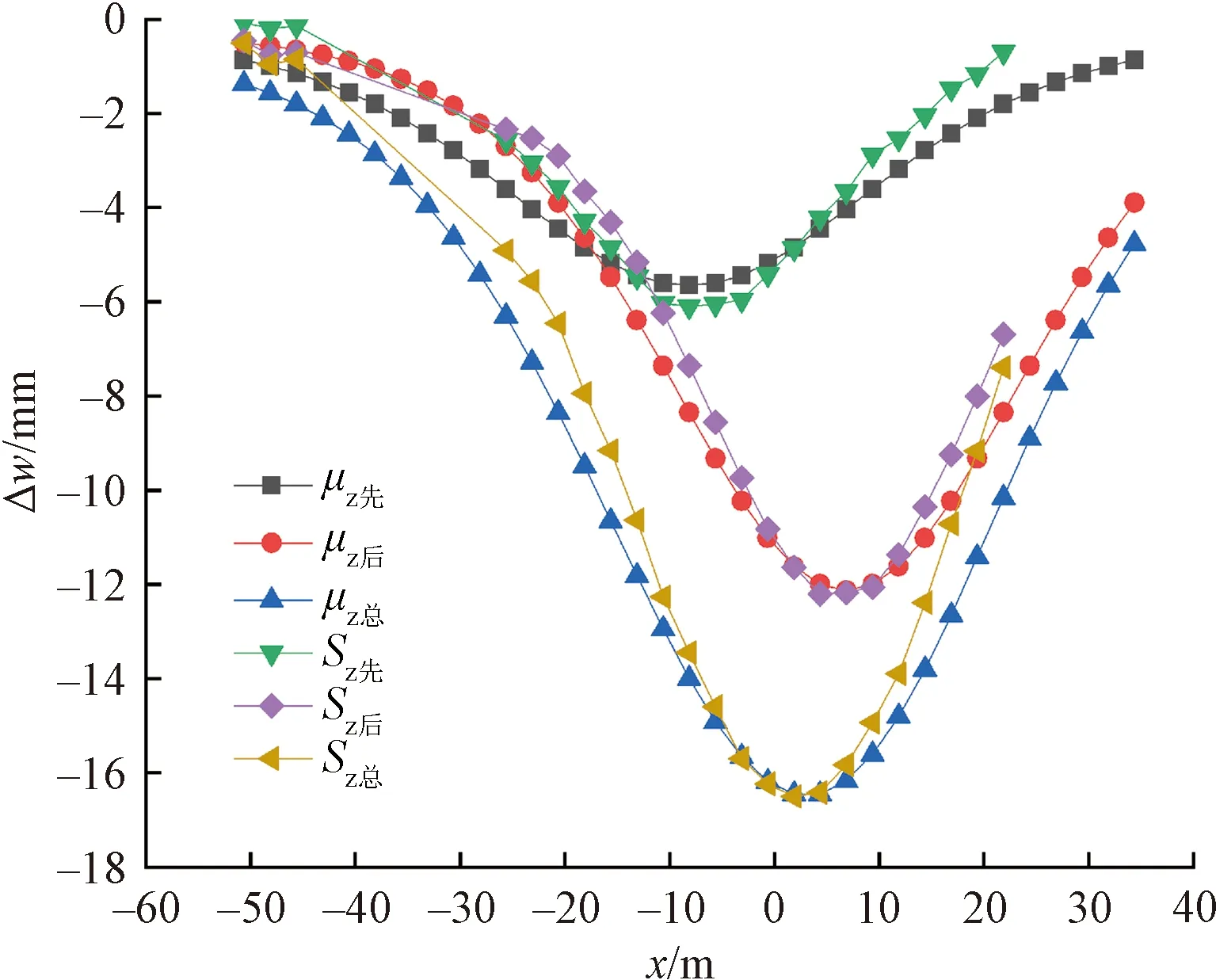
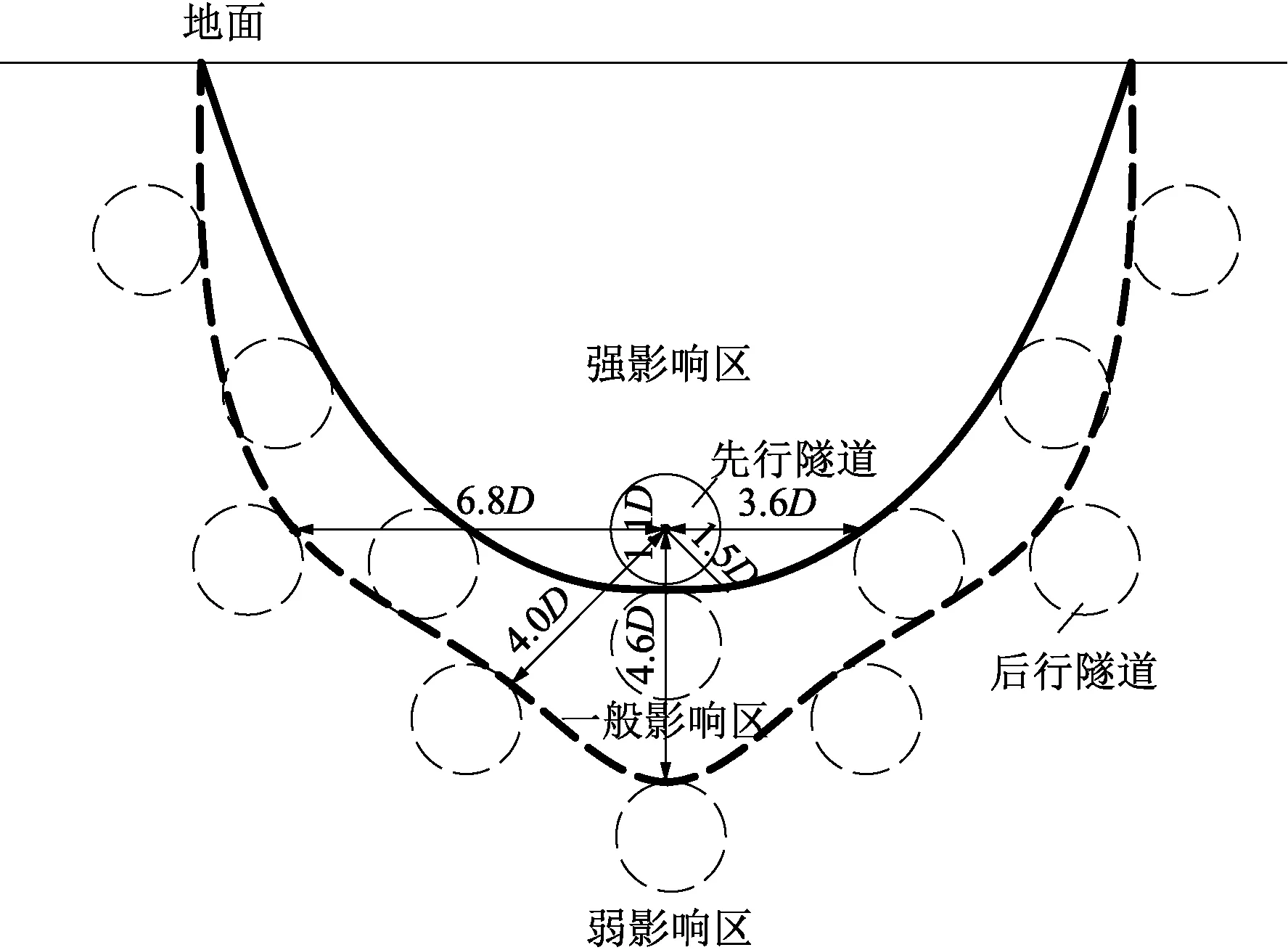
由图10可知，当盾构未到达监测断面时，盾壳摩擦力与土体损失引起的地表变形最为明显，主要原因是盾壳与周围土体摩擦力较大，且作用面比附加推力和盾尾注浆广，而土体损失是引起地表变形的主要因素。刀盘附加推力、盾壳摩擦力引起的地表增量变形曲线分别关于y=0、y=5 m(L/2)呈中心对称，注浆压力引起的地表增量变形曲线关于y=11 m(1.0L)成轴对称；当后行盾构刀盘距离断面前方约18 m(5Rs)时，地表开始产生沉降，这与先行盾构(3Rs)相比，沉降开始时间更早；当后行盾构刀盘位于监测断面正下方时，计算得地表相对增量位移(Δw/Δwmax)约31.4%，较先行盾构(约23%)大，这意味着后行盾构受到黏土的滞后效应相对减弱；当地表相对增量位移达到50%时，盾构此时经过监测断面5～10 m，即刀盘位于5 m

基于本文计算结果，通过与经典的Mindlin解及丁智解进行对比，来验证本文施工参数修正后的准确性，结果见图11。由图11可知，Mindlin解及丁智解计算的变形沉降(隆起)量比本文预测结果更大，且丁智解计算得出的隆起量较Mindlin解更明显，而沉降量恰好相反。这是因为，盾构前期施工参数对地表变形的影响比土体损失更大，其中，盾壳摩擦力是引起地表变形的主要因素，而原盾壳摩擦力计算公式因忽略了土体软化及浆液漫延润滑盾壳壁的影响，导致计算结果偏大；丁智解较Mindlin解考虑了饱和土特性，假定土体不可压缩，所以，在计算土体损失引起的地表变形时，沉降量会略小。对比结果表明，本文计算结果与实测结果更为接近，再次验证了本文计算方法的正确性。

图11 纵向地表增量变形对比图

先行、后行隧道施工引起的横向地表变形见图12，μz先、μz后、μz总分别为理论计算得出的先行、后行隧道施工引起的地表增量变形及地表总变形，Sz先、Sz后、Sz总分别为实测得出的先行、后行隧道施工引起的地表增量变形及地表总变形。由图12可知，后行盾构施工引起的最大增量沉降约12 mm位于后行隧道轴线左侧的第一个监测点x=6.875 m(YSMP17)处；后行盾构的地表变形影响边界范围在YSMP3～YSMP4之间，即-45.625 m

图12 先行、后行隧道施工引起的横向地表变形

2.2 规律分析

仍以海德公园盾构隧道工程为例，取不同工况进行分析，工况信息如下：

先行隧道轴线埋深分别为20、25、30、35 m，先行、后行隧道的水平夹角分别取90°、45°、0°、-45°、-90°(逆时针为正，顺时针为负)，两隧道轴线间距分别取1.0D、2.0D、3.0D、4.0D、5.0D、6.0D、7.0D、8.0D，先后计算两组数据，第一组数据中后行盾构刀盘附加推力、盾壳摩擦力、注浆压力、土体损失率需考虑先行隧道的影响，并根据位置不同进行计算，第二组数据忽略先行隧道施工对后行隧道的影响，仅考虑位置不同导致的施工参数变化，土体参数均保持不变，两组数据共计320种工况，为了数据的合理性，去除了隧道埋深小于3D的工况。

2.2.1 二次扰动效应研究

为研究先行隧道对后行隧道的影响，选取施工过程中地表最大沉降点进行分析，结果见图13。先行、后行隧道位置见图14。图14中，极点为先行隧道的中心，极轴为考虑先行隧道施工影响地表最大沉降量，数据点为后行隧道位于不同位置时考虑先行隧道施工影响的地表最大沉降量。由图13可知，当先行、后行隧道的相对位置不变，仅改变整体埋深时，可发现埋深越浅，地表变形越明显，且随着埋深逐渐减小，变化速率则逐渐加快。

图13 地表最大沉降雷达

图14 先行、后行隧道相对位置

为进一步研究先行隧道施工对后行隧道的影响程度，将考虑先行隧道影响前后的地表最大沉降值做差，结果见图15，δ为两组数据的地表沉降差值，差值越大表示二次扰动效应越明显。因隧道左右对称，故本文仅考虑隧道水平夹角为-90°≤β≤90°时的地表沉降差变化，为方便后续描述，根据后行隧道所在位置不同，分成4小区间：

(17)

图15 考虑先行隧道施工影响前后地表最大沉降差值

由图15可知，当先行、后行隧道埋深相同时，即β=0，隧道间距越小，后行隧道受到先行隧道施工引起的二次扰动效应越强，沉降变化速率越快，地表沉降量也越大；当后行隧道的相对埋深越深(对于上穿及侧上穿区间，隧道间距越小埋深越深，而对于下穿及侧下穿区间则恰好相反)，受到的二次扰动效应越弱。究其原因：①当后行隧道位于下穿或侧下穿区间时，其扰动参量，即S3与S2的比值随着隧道埋深的增加而逐渐减小，计算得到的后行隧道土体损失率也会相应减小，二次扰动效应相对减弱；②当后行隧道位于任意区间时，其隧道埋深越深，隧道周围的地应力也越大，当隧道开挖达到卸荷条件时，土颗粒相互间的黏聚力会急剧下降，从而在深部土层形成土拱效应，减弱二次扰动的影响。这与文献[33]中的分析相一致，当隧道周围土体位移过大时，会产生一定程度的应力松弛，致使土体产生剪切作用，发挥土拱效应，而深部土体的最大主应力方向会偏转至斜向以及水平向，增大土体侧压力系数，土拱效应更明显。

当先行、后行隧道间距不变，后行隧道位于侧上穿区间时受到二次扰动影响随角度变化的速率最大，位于上穿与侧下穿区间时的变化率近似相同，而位于下穿区间的变化率最小，其结果分析见表1。后行隧道位于上穿区间和下穿区间时，隧道埋深z1随角度的变化率明显比位于侧穿区间的小，而扰动参量ξ随角度的变化率各有不同。

表1 二次扰动影响程度分析

为研究先行隧道施工引起的二次扰动效应范围界限，将考虑先行隧道施工影响前后的最大地表沉降差值与未考虑先行隧道施工影响的最大地表沉降量的比值定义为二次扰动影响率，记为Dis。假设当Dis≥0.5时为强影响区，当0.2≤Dis≤0.5时为一般影响区，当Dis≤0.2时为弱影响区，二次扰动效应范围界限见表2。

表2 二次扰动效应范围界限

由表2给出的二次扰动效应范围界限见图16，与张治国等[17]的研究结果较为一致，当平行隧道轴心间距达到6D时，两条隧道的沉降峰值线与水平夹角接近于90°，即二次扰动影响较弱，验证了本文所得规律的准确性，但其仅概括了双线平行隧道施工的情况，而本文得出的规律范围更广，界限更明确，能适用于先行、后行盾构任意位置施工时的工况。

图16 二次扰动效应范围界限

2.2.2 沉降槽峰值位置变化研究

为避免双线盾构施工引起的地表变形超过警戒值，需预测地表沉降槽峰值所在的位置。考虑先行隧道的影响，当后行隧道正上穿或下穿先行隧道时，两隧道轴线上下叠交，此时地表沉降槽峰值点位于x=0位置。所以，在研究双线盾构施工引起地表沉降槽峰值所在位置的变化规律时，仅考虑双线水平及斜交布置的情况，计算结果见图17。

图17 水平夹角为0°、-45°时的沉降槽峰值所在位置

图17中的辅助线为隧道轴线与坐标中心的距离，由图17可知，当两隧道水平夹角为0°时，即为双线平行盾构，隧道间距较小时，沉降槽峰值点位于后行隧道轴线与坐标中心的中点，随着隧道间距逐渐增大，峰值点的位置逐渐靠近后行隧道中心，最终与后行隧道轴线位置重合。这是由于受到先行隧道二次扰动的影响，导致后行隧道施工引起的沉降槽峰值明显大于先行隧道，当隧道间距较近时，先行、后行隧道沉降槽曲线叠加后中间部分的土体累计变形量大于后行隧道施工引起的最大变形量，导致沉降槽峰值点偏离后行隧道，位于隧道轴线和坐标中心之间的区域。当隧道埋深越浅，后行隧道受到的二次扰动效应越明显，施工引起的地表沉降量也越大，使得先行、后行隧道施工引起的地表沉降槽峰值点更接近后行隧道中心。当两隧道水平夹角为-45°时，此时随着隧道间距的增加，不仅先行隧道对后行隧道的二次扰动效应减弱，且由于后行隧道的埋深增加，致使后行隧道施工引起的地表沉降量逐渐减小，所以，先行隧道施工引起的地表沉降量会随着隧道间距的增加逐渐大于后行隧道，且沉降槽峰值点靠近隧道轴线的速度较双线水平布置的情况更缓慢，最终与先行隧道轴线保持在一个稳定的间距，沉降槽峰值位置变化的研究再次验证了本文二次扰动规律的正确性。

2.2.3 先行、后行隧道不同施工间隔研究

先行隧道施工会对土体产生扰动，其结构强度会剧烈降低，但随着盾构向前推进，土体的结构和强度又会随着时间逐渐恢复，对于大多数的黏土-水体系，这种触变性是普遍存在的[34]。为研究触变性对后行盾构施工的影响，将先行、后行盾构施工间隔分别取0、10、20、50、100 d，其余参数不变，结果见图18。

图18 先行、后行盾构不同施工间隔对地表变形的影响

由图18可知，双线盾构同时施工引起的地表沉降量最大，随着先行、后行隧道施工间隔逐渐加长，土体强度逐渐恢复，先行隧道施工对土体的扰动效应逐渐减弱，后行隧道施工引起的地表变形逐渐减小，故总地表沉降量也逐渐变小。而且，土体强度在前期恢复较快，后期恢复速率逐渐变慢，在100 d时已达到了基本稳定状态，故建议后行盾构施工时间建议在先行盾构施工完成3个月后较为安全。

3 结论

本文基于半无限饱和土初值解，充分考虑了多种施工因素和先行、后行盾构位置及施工间隔不同对后行隧道土体二次扰动的影响，修正了现有饱和土双线盾构施工引起的土体变形计算公式，并结合典型的伦敦饱和黏土工程案例，通过与Mindlin解、丁智解进行对比分析，结论如下：

(1) 考虑了挤土效应、浆液漫延、土体软化、浆液自重、注浆压力环向不均匀分布以及浆液填充盾构间隙等施工因素后，计算双线盾构施工引起的地表变形解与Mindlin解、丁智解相比，其结果与实测曲线更接近，可以较为准确地反映盾构掘进过程中纵向、横向地表变形的特点。

(2) 当双线隧道平行布置，由于先行隧道二次扰动效应的影响，后行隧道受到土体的滞后效应减弱，但先行、后行隧道的影响范围基本一致；隧道间距越小，二次扰动效应越强，沉降变化速率越快，地表沉降量也越大，沉降峰值点越接近坐标中心；随着隧道间距逐渐增大，沉降槽峰值点的位置逐渐靠近后行隧道中心，最终与隧道轴线重合。

(3) 当双线隧道斜交布置，隧道间距不变时，后行隧道位于侧上穿区间受到二次扰动影响随角度变化的速率最大，位于上穿与侧下穿区间的变化率近似相同，而位于下穿区间的变化率最小；隧道间距逐渐增大时，二次扰动效应的减弱及后行隧道的埋深增加致使后行隧道施工引起的地表沉降量逐渐减小，先行隧道施工引起的地表沉降量会逐渐大于后行隧道，最终沉降槽峰值点会与先行隧道轴线保持在一个稳定的距离。

(4) 二次扰动效应主要体现在土体受扰动后其结构强度会剧烈降低，但随着盾构向前推进，土体的结构和强度又会随着时间逐渐恢复，故当双线盾构同时施工时引起的地表沉降量最大，随着先行、后行隧道施工间隔逐渐加长，土体强度逐渐恢复，先行隧道施工对土体的扰动效应逐渐减弱，后行盾构施工引起的地表变形逐渐减小，故总地表沉降量也逐渐变小。