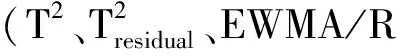基于One-class SVM的自相关线性轮廓监控研究
薛 丽,贾元忠,曹逗逗
(郑州航空工业管理学院 管理工程学院,河南 郑州 450046)
1 引 言
统计过程控制(SPC)应用中,通常运用传统控制图监控一元或者多元质量特性值。如果一个产品的质量特性值可以用多个响应变量与多个自变量之间的函数关系表示,则可以采用轮廓控制图监控该产品的质量特性值,此时这种函数关系称为轮廓。为了监控半导体工业校准过程中的稳定性,2000年Kang 和Albin[1]对压力和流量之间的关系用简单线性轮廓模型进行描述,并提出相应轮廓监控方法。简单线性轮廓模型易于处理且可应用于许多生产过程,许多学者先后对涉及简单线性轮廓监控进行了相关研究(Woodall等[2],Wang 和Tsung等[3])。
SPC第一阶段主要分析生产过程是否稳定,并对生产过程中的参数进行估计,其中Mestek 等[4]、Kim等[5]、Taghipourde等[6]对控制图的第一阶段方法进行研究。SPC第二阶段对生产过程进行监控,当过程中存在异常波动时控制图报警。Kang和Albin[1]提出了T2、指数加权移动平均(EWMA)联合R控制图的方法,以监控线性轮廓的变化。Kim等[7]对变量数据进行中心化处理,使用EWMA控制图对参数进行监控。Abbas等[8]构造了三种单变量贝叶斯EWMA控制图,分别对截距、斜率和误差方差进行了监控。Abbas等[9]将贝叶斯理论用于累积和(CUSUM)控制图,研究表明,在共轭先验下提出的CUSUM控制图性能更佳。Huwang等[10]运用空间秩的EWMA图对误差项不符合正态性假定的线性轮廓进行监控研究。Haq等[11]通过调整可变抽样区间提高控制图的灵敏度。Yeganeh等[12]提出了一种多元指数加权移动平均(MEWMA)控制图和运行规则相结合的方法,提高了监控简单线性轮廓的性能。Zhang等[13]使用CUSUM控制图对预先指定的线性轮廓变化进行监控。Noorossana等[14]研究了第一阶段参数估计误差对第二阶段轮廓监控的影响。
随着生产过程中数据采集技术的发展以及抽样间隔越来越短,许多轮廓数据具有自相关性,此时应用传统独立过程的监控方法会大大增加虚发警报[15]。针对误差项遵循一阶自回归模型AR(1)的简单线性轮廓,Soleimani 等[15]提出了T2控制图和EWMA控制图来监控生产过程。Chiang等[16]提出了MEWMA控制图,用于检测截距和斜率的变化。
以上研究均是基于构造统计量建立控制图以监控生产过程,需要对原始数据进行处理,其过程较为复杂。控制图可以看成区分受控过程和失控过程的分类器,因此使用机器学习方法可以监控生产过程,且不需要对数据进行复杂的处理,亦能达到较好的效果。Hosseinifard等[17]以及Yeganeh和Shadman[18]运用神经网络对线性轮廓监控进行了研究。贺辰然[19]讨论了二分类支持向量机在监控线性轮廓中的应用。二分类的方法需要大量受控和失控样本训练分类器,但在实际生产过程中,这一条件有时不能得到满足,因此在一定程度上限制了其应用范围。针对实际生产过程中仅有受控样本的情况,SVDD方法被引入轮廓监控中,且取得了不错的效果[20-22]。
在以上研究背景下,为尽快监测出自相关线性轮廓数据的异常,本文针对实际生产过程中异常类样本难以收集或者收集异常样本需要消耗大量的时间或成本的情况,提出基于一类支持向量机(OCSVM)[23-24]的监控方法。以平均运行长度(ARL)为准则,通过仿真实验讨论不同核函数对监控性能的影响,并将结果与现有的一些传统方法进行比较。
2 方法简介
OCSVM是基于支持向量机(SVM)的一种一类分类器[23-24]。模型描述如下:设有受控训练样本{z|zi∈Rn,i=1,2,…,m},坐标原点坐标为(0,0,…,0)nx1,通过核函数将训练样本映射到高维特征空间,在特征空间中找到一个最优超平面实现训练样本与坐标原点的最大分离。最优超平面表达式为w·z-b=0,w为权重向量,b为偏差。使最优超平面与坐标原点的距离b/‖w‖最大,转化为二次规划问题:
s.tw·zi-b+ξi≥0,ξi≥0.
(1)
其中ξi为松弛变量,u为训练样本中噪声数据比例。用拉格朗日方法将式(1)转化为无约束最优化问题,即:
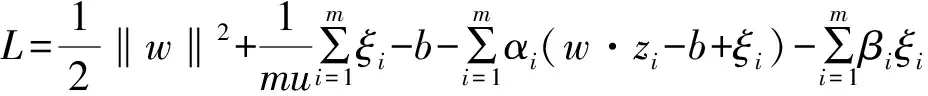
(2)
其中αi≥0,βi≥0为拉格朗日乘子。对式(2)中的变量w,b,ξ分别求导并令偏导数为0可得:
(3)
(4)
(5)
将得到的式(3)~(5)带入式(2)可将原问题转化为其对偶问题,并将对偶问题求最小可得:
(6)
式(6)中(zi·zj)为内积运算,OCSVM中用核函数代替内积运算。式(6)可以转化为:
(7)
对二次规划问题式(7)进行求解,可得到拉格朗日乘子α=(α1,α2,…,αm),其中αi不为0,对应的zi为超平面的支持向量。对新的测试样本o,该点所属类别的判别式为:
(8)
根据f(o)的输出值判断测试样本o的所属类别。如图 1所示,以二维数据说明OCSVM的原理。
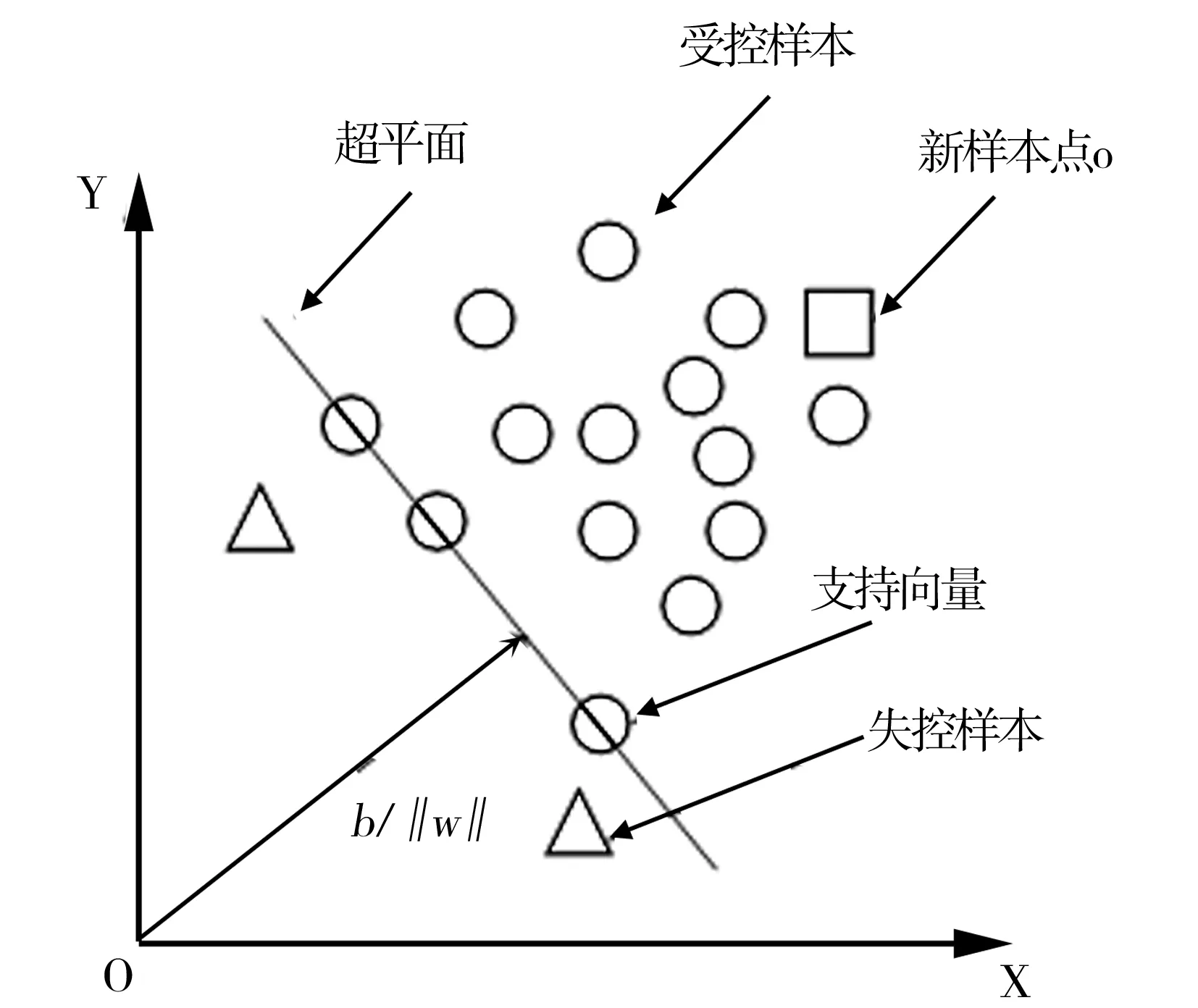
图1 用于异常检测的二维OCSVM示意图图解
若f(o)≥0,则测试样本o属于受控类,若f(o)<0,则测试样本o属于失控类。
3 基于OCSVM的线性自相关轮廓监控模型
3.1线性自相关轮廓
假设过程或产品质量特性Y为某一变量X的函数,过程处于统计受控状态时,Y与X的函数关系为:
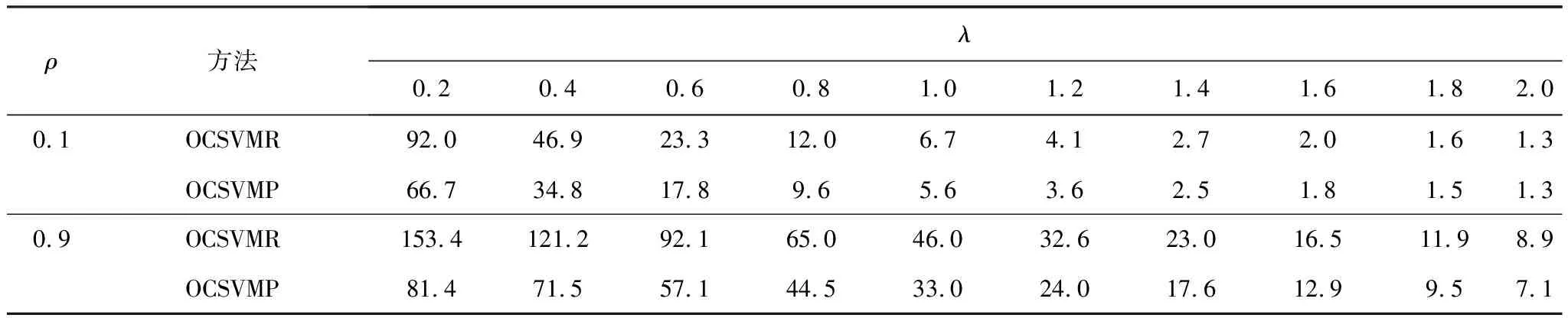
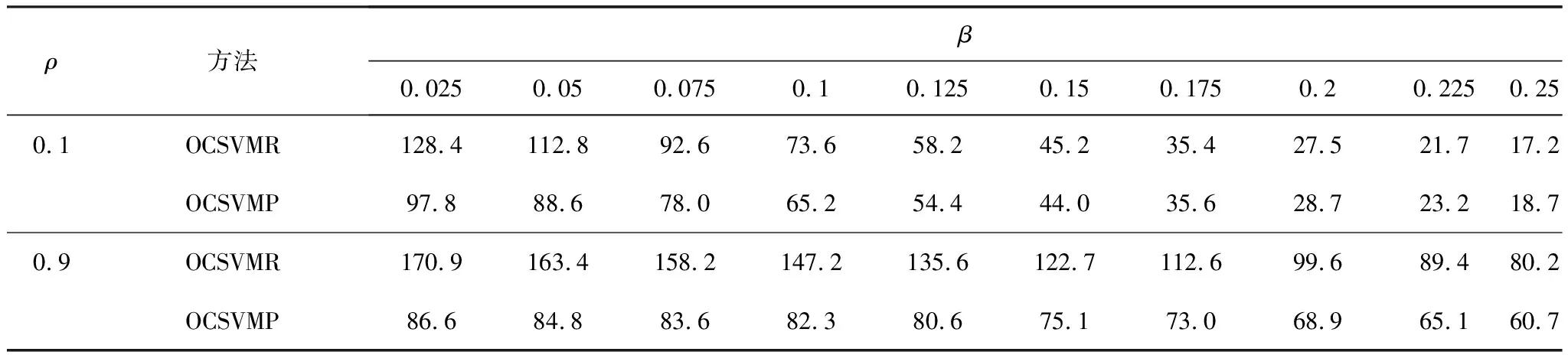
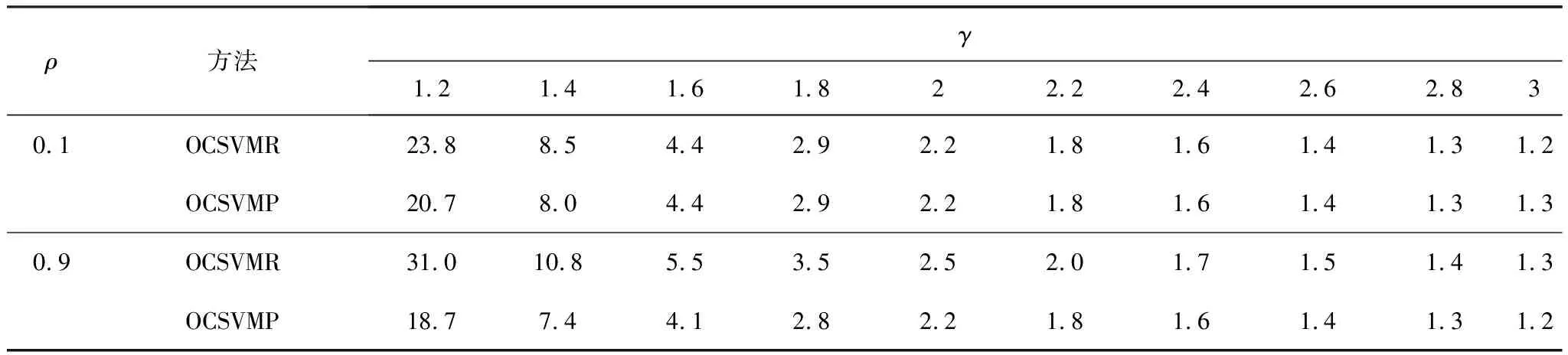
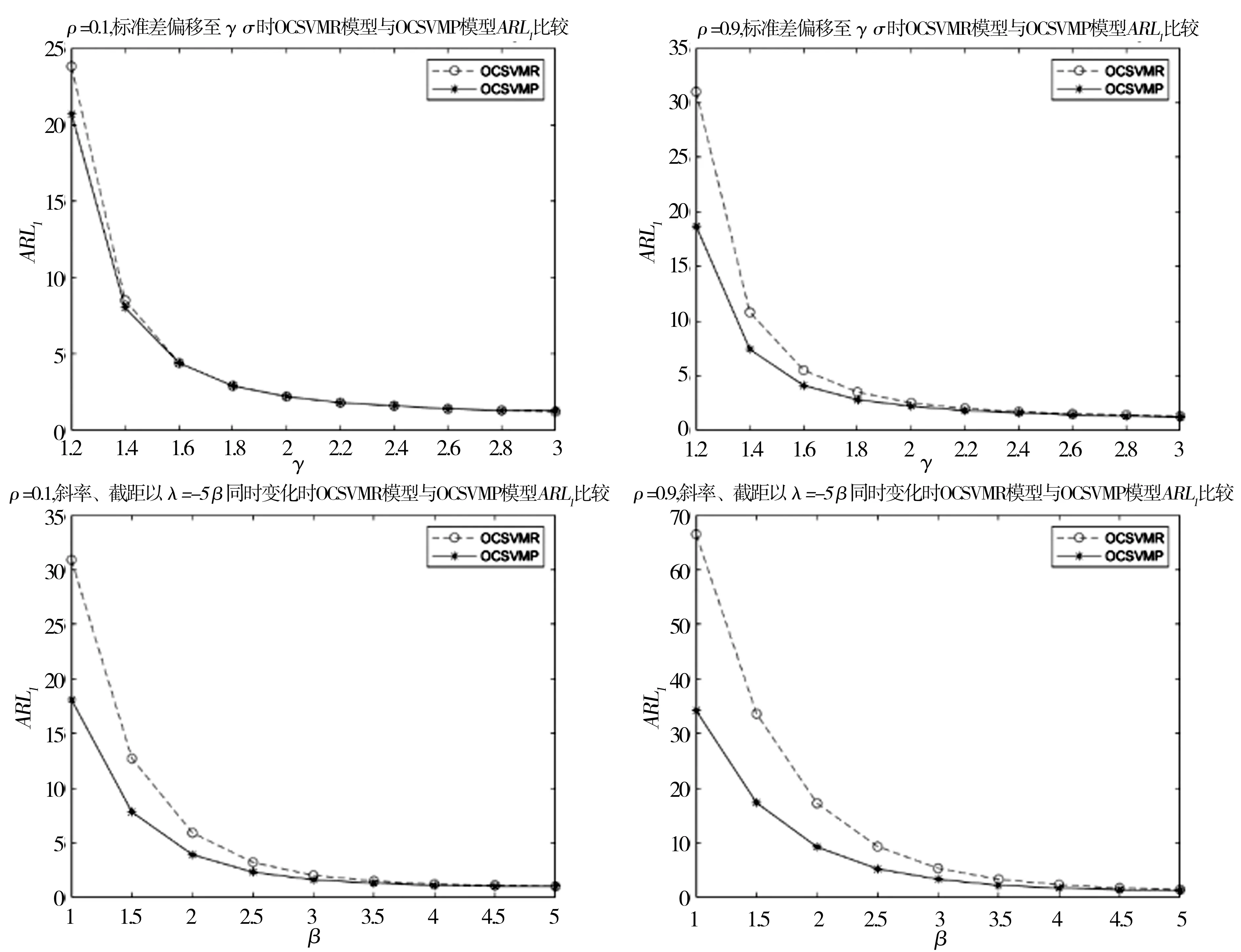
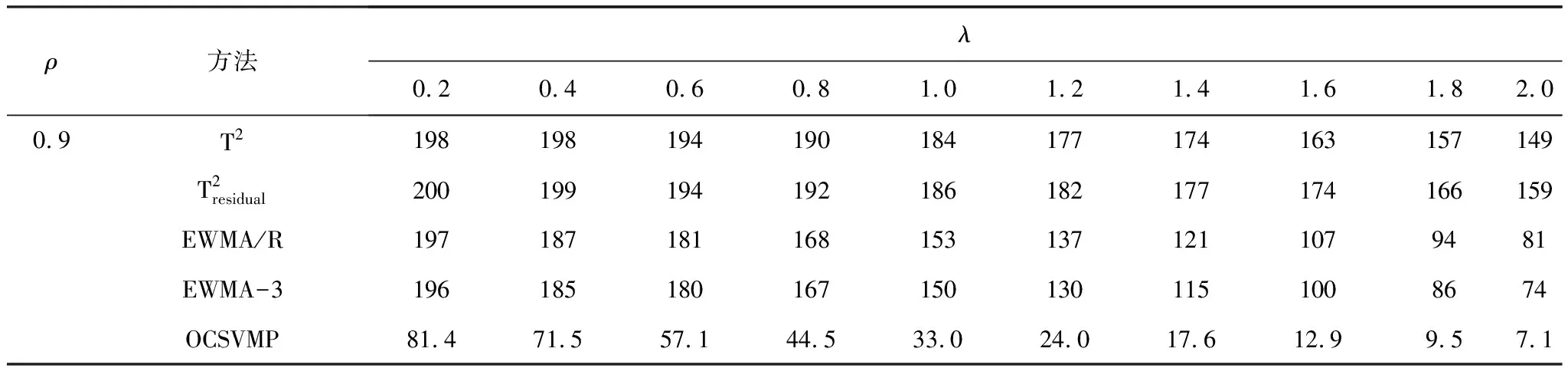
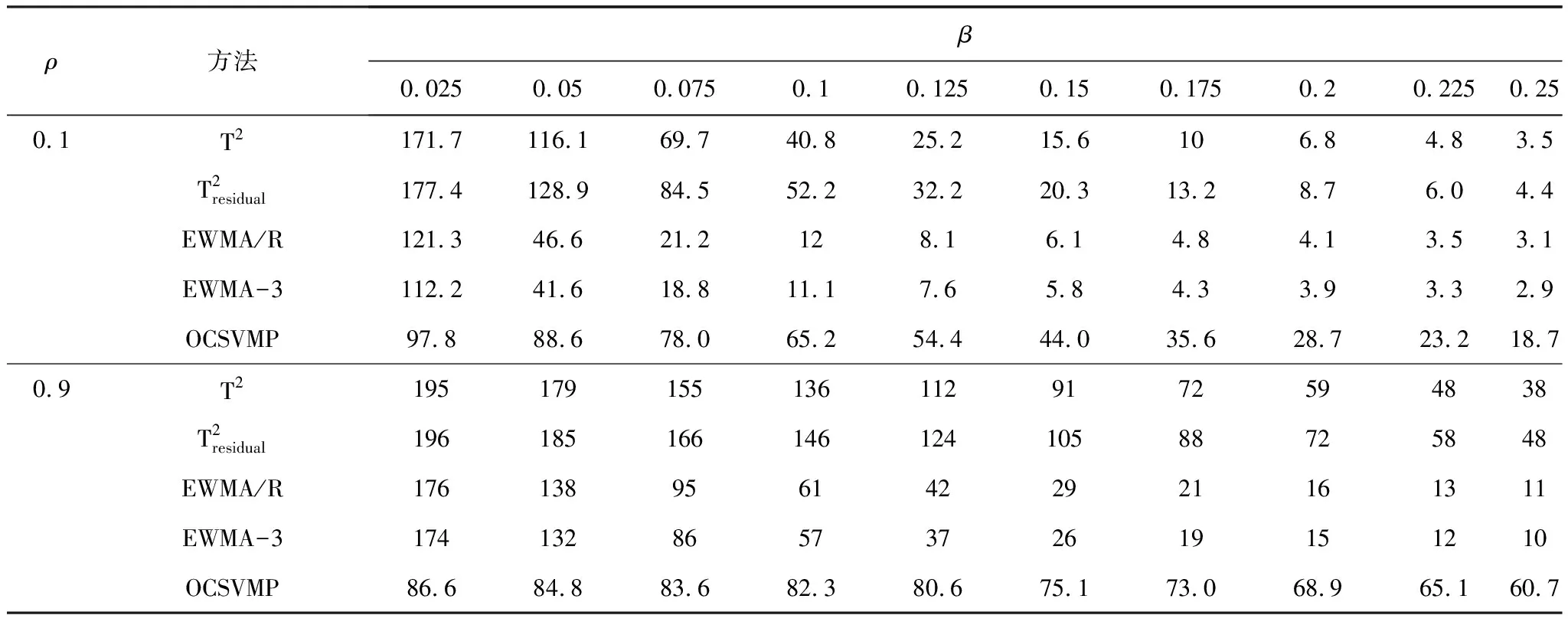
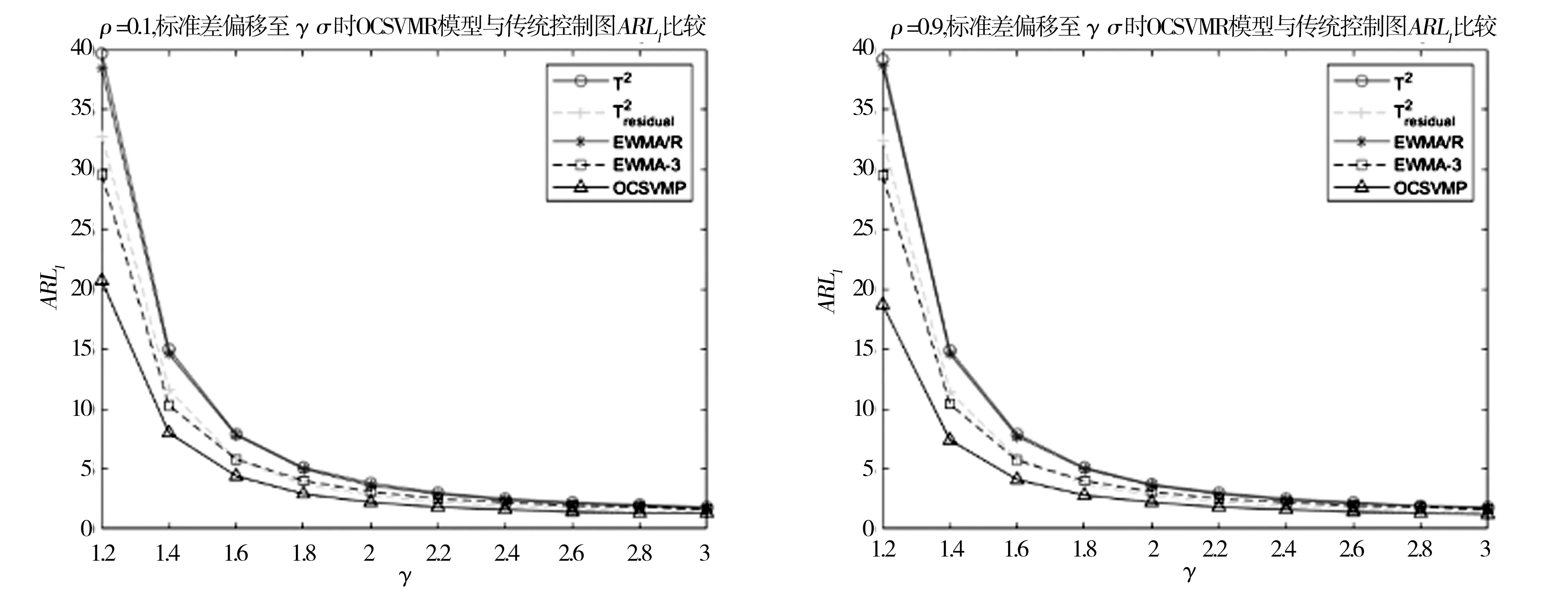
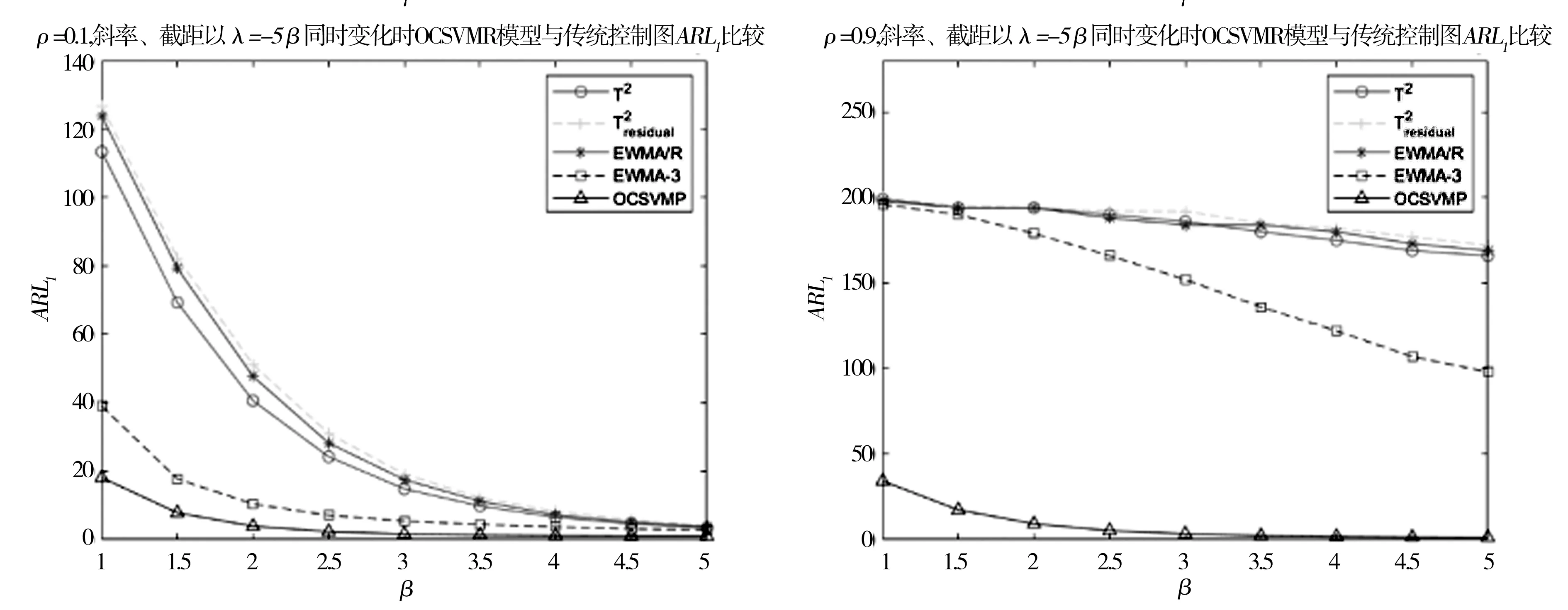
Y=f(X,β)+α,Xι (9) 其中,β为受控轮廓的系数向量,Xι和Xh界定了的X的范围,α为独立随机变量且服从均值为0、方差为σ2的正态分布。上述独立变量X可以是时间、加工产品的测量位置、温度等。 对抽样时刻i(i=1,2,…,m),可以测得轮廓内n个观测点xi1,xi2,…,xin响应变量的值为yi1,yi2,…,yin。每条轮廓为一个观测样本,每个样本由n个数据点(xij,yij),j=1,2,…,n构成。为方便分析数据,常假设不同轮廓中点(Xι,Xh)内观测点位置相同,即对任意时刻i的轮廓有xij=xj。用AR(1)模型表示线性轮廓内的相关性[15]。过程处于统计控制状态时,线性轮廓内自相关模型可以表示为: yij=A0+A1xj+εij εij=ρεi(j-1)+αij (10) 其中εij为相关误差项,αij为独立随机变量且服从均值为0、方差为σ2的正态分布。ρ是自相关系数,为已知常数。本文中,考虑第二阶段,即假设参数A0,A1,σ2已知。 图2 OCSVM方法流程图 利用训练阶段得到的超平面对后续新收集的轮廓数据进行监控,判断其生产过程是否处于受控状态,如果存在异常原因,则发出警报。OCSVM控制方法的结构如图3所示。 图3 OCSVM控制方法结构图 为验证所提出方法的监控效果,采用Soleimani等[15]的仿真模型来进行模拟。每个轮廓的截距A0=3,斜率A1=2,回归方程为: yij=3+2xj+εij, εij=ρεi(j-1)+αij, (11) 其中εij是相关误差项,αij为独立随机变量,且αij~N(0,1),ρ为自相关系数。在模拟仿真中,分别针对自相关系数ρ=0.1(弱相关)或ρ=0.9(强相关)两种情况,所提出的方法与Soleimani等[8]提出方法的监控效果进行比较。 假定式(7)中的训练样本噪声数据比例u=0.001。针对自相关系数ρ=0.1(弱相关)或ρ=0.9(强相关)两种情况,分别采用高斯核函数和多项式核函数进行训练,并将这两种训练模型的监控效果进行比较,选择对具有自相关性的轮廓数据监控效果较好的核函数。最后与Soleimani等[15]提出的方法进行比较。 以平均运行长度为评价准则对不同控制图性能进行比较。首先确定OCSVM方法参数,训练阶段调整参数令控制图误警率α=0.005,即受控运行长度ARL0=200,然后比较失控运行长度ARL1,ARL1越小的控制图监控性能越好。 β=(-0.2,-0.3,-0.4,-0.5,-0.6,-0.7,-0.8,-0.9,-1)同时变化的9种异常。 以ρ=0.1(弱相关)时为例,(ρ=0.9过程同ρ=0.1)仿真步骤如下: 步骤一:生成训练数据。根据式(11)生成M个受控样本数据,样本类别为+1。 步骤二:数据预处理。将步骤一生成的样本值转化到[0,1]的区间内。 步骤三:确定核函数及核函数参数。本文选取高斯和多项式两种核函数进行比较。 步骤四: 寻找最优参数。在[2-10,210]范围内采用遍历法调整核函数参数,使训练数据的误警率为0.005,误差为0.0001。训练时对受控数据采用10折交叉验证的方式,将受控数据随机分成10份,其次轮流将其中9份做训练1份做验证,10次结果的均值作为对算法精度的估计值,使训练数据最终的误警率为0.005,受控运行长度ARL0=200。 步骤五:构建模型。由步骤四得到最优参数,对训练样本训练得到分离超平面,对后续过程进行监控。 步骤六:生成异常数据。对4类异常数据每种异常生成1000批数据集,每批数据集含有1000个对应的异常数据。 步骤七:计算ARL1。采用步骤五中得到的分离超平面对步骤六中的异常样本进行监控,由于每种异常有1000批数据集,故迭代1000次之后得到的均值即为ARL1。 运用高斯核函数与多项式核函数的训练模型分别记为OCSVMR、OCSVMP。在受控运行长度ARL0相同的情况下,通过比较不同控制方法对应的失控平均运行长度ARL1值的大小来评价其性能。采用上节中的步骤进行仿真模拟,表1—4显示了ρ分别为0.1和0.9时截距变化、斜率变化、标准差变化以及截距、斜率同时变化的失控运行长度,其中λ、β、γ分别为截距、斜率、标准差的变化量,变化单位为σ。 表1 截距A0偏移至A0+λσ时OCSVMR模型与OCSVMP模型ARL1比较 表2 斜率A1偏移至A1+βσ时OCSVMR模型与OCSVMP模型ARL1比较 表3 标准σ差偏移至γσ时OCSVMR模型与OCSVMP模型ARL1比较 表4 斜率、截距以同时发生偏移时OCSVMR模型与OCSVMP模型ARL1比较 为直观显示OCSVMP模型与OCSVMR模型的监控效果,下面用图形的方式对表1—4中的情况进行比较,具体见图 4。 图4 OCSVMR模型与OCSVMP模型监控效果比较 由图4可知,监控截距发生偏移时,OCSVMP模型优于OCSVMR模型。监控斜率方面,在自相关系数ρ=0.1,斜率偏移小于0.175时,OCSVMP模型优于OCSVMR模型;自相关系数ρ=0.9时,OCSVMP模型优于OCSVMR模型。监控标准差方面,OCSVMP模型整体优于OCSVMR模型。另外,在监控截距、斜率同时变化时,OCSVMP模型整体优于OCSVMR模型。从整体看,OCSVMP模型的监控效果优于OCSVMR模型。 表5 截距A0偏移至A0+λσ时OCSVMP模型与传统控制图ARL1比较 续表5 截距A0偏移至A0+λσ时OCSVMP模型与传统控制图ARL1比较 表6 斜率A1偏移至A1+βσ时OCSVMP模型与传统控制图ARL1比较 表7 标准差σ偏移至γσ时OCSVMP模型与传统控制图ARL1比较 表8 斜率、截距以同时发生偏移时OCSVMP模型与传统控制图ARL1比较 续表8 斜率、截距以同时发生偏移时OCSVMP模型与传统控制图ARL1比较 为直观显示OCSVMP模型与传统控制图的监控效果,下面用图形的方式对表5—8中的情况进行比较,具体见图 5。 图5 OCSVMR模型与传统控制图监控效果比较 由图5可知,监控截距发生偏移时,自相关系数ρ=0.1,在截距偏移大于1.2时,及自相关系数ρ=0.9时,OCSVMP模型优于另外四种方法。监控斜率偏移时, EWMA-3方法表现最优。监控标准差发生偏移时,OCSVMR模型整体优于另外四种方法。监控截距、斜率同时变化时,OCSVMP模型明显优于另外四种方法。3.2基于OCSVM的监控模型
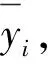

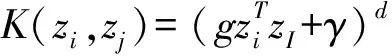

4 仿真分析
4.1仿真过程

4.2不同核函数监控性能对比
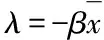
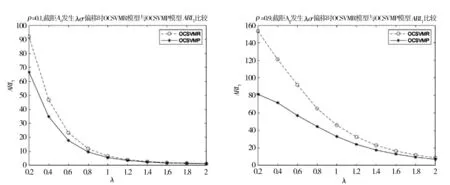

4.3与传统控制图方法比较研究
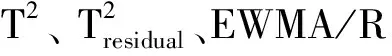


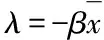
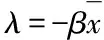

5 结 论