含甲烷水合物的玻璃珠渗透率实验与簇状等径颗粒模型

肖长文，李小森，李刚，余杨，余建星，李世龙，吕秋楠

(1.天津大学水利工程仿真与安全国家重点实验室，天津，300072；2.中国科学院广州能源研究所，广东广州，510640；3.中国特种飞行器研究所，湖北荆门，448004)

水合物[1]是一种包含水分子和气体分子的固态晶体，在高压低温的环境中，气体分子被束缚在由水分子生成的笼型骨架，形成稳定的气体水合物。天然气水合物主要分布于永久冻土层和深海地层之中[2]。海洋天然气水合物由于其分布广、储量大和集输便捷等特点，成为天然气资源开发的热点。目前天然气水合物的开采常用的方法有降压开采法[3]、注热开采法[4]、抑制剂注入法[5]以及二氧化碳置换开采法[6]等，每一种开采方式拥有各自的优势，都能实现水合物储层的合理高效开发。在含天然气水合物的海底沉积物层的开发中，需要评价储层的气体饱和度、孔隙度和气水渗流性等储层参数。固态天然气水合物占据沉积物的孔隙空间，阻塞气水流动通道，从而影响产气产水效率。因此，研究多孔介质渗透率特性随水合物饱和度的变化，对天然气水合物藏的开发具有重要意义。

含水合物多孔介质的渗透率的实验研究主要包含多孔介质类型、水合物晶体结构、水合物生成方法以及渗透率测量方法等方面，但实验结果的可靠性和可重复性需要深入研究。MINAGAWA等[7]采用过量水法在不同种类多孔介质中生成甲烷水合物，并通过稳态注水测量了不同水合物饱和度下的有效渗透率，发现当水合物饱和度较低时，渗透率的下降趋势更明显。LI等[8]在高压反应釜内填充粒径为300～400 μm 的石英砂，用水过量的形式生成甲烷水合物，采用稳态注水测得沉积物的水相渗透率，发现适当控制水的注入速率，可有效降低水合物的分解。JOHNSON 等[9]使用来源于阿拉斯加北坡(ANS)埃尔伯特山站点的含天然气水合物岩心样品，采用注入盐水和氮气的方法测量岩心的渗透率，发现非稳态相对渗透率测量会导致活塞位移现象，且在较低水合物饱和度情况下，岩心样品的渗透率明显下降。吕勤[10]以BZ-01型和BZ-02型玻璃珠为多孔介质，在过量甲烷气体下生成水合物，并以稳态甲烷气体测量了含甲烷水合物沉积物气相渗透率，发现水合物在孔隙中的形态由初期注入的气体与水的比例控制，当2种玻璃珠初始水饱和度分别大于40%和35%时，水合物更倾向于孔隙中心生长，而当初始水饱和度低于这一临界值时，水合物倾向于在颗粒表面生成。水合物的赋存形式分为颗粒包裹型和孔隙中心填充型。在水合物生成时，气体与水的比例影响其在孔隙空间的分布方式，且注水法和注气法的渗透率测量方法也会有不一样的效果。

对于含水合物多孔介质的渗透率模型，KLEINBERG等[11]总结了含水合物的平行毛细管模型和等径颗粒模型，其中，平行毛细管模型[12]假定多孔介质孔隙由毛细管束组成，等径颗粒模型假定多孔介质是由等径圆球颗粒堆积而成，2种模型都量化了多孔介质的孔隙度和比表面积等参数，平均化表征孔隙空间分布。在此基础上，LI等[13]研究了粒径和水合物饱和度对石英砂多孔介质渗透率的耦合影响，提出了2个水合物孔隙填充渗透率模型，在粒径不同的石英砂介质中，水合物饱和度低于10%和高于10%时，渗透率下降特征不同，且水合物对多孔介质渗透率有显著影响。SHEN等[14-15]将等径颗粒模型和MASUDA模型进行耦合，考虑了水合物对孔隙内表面积的影响，建立了多种规则球体填充模型。DAI 等[16]从孔隙尺度出发，假定水合物颗粒在多孔介质中随机分布，建立了孔隙网络模型，修正流线的迂曲度，通过数值模拟方法获得含水合物饱和度的经验公式。陈浩等[17]通过原位扫描电镜直接观测含盐体系蒙脱土中甲烷水合物生成和分解过程，水合物在蒙脱石表面呈现独立颗粒状，水合物颗粒表面光滑，颗粒与颗粒之间具有明显的生长界限。

水合物饱和度增加会伴随着水合物颗粒增多并聚集成簇。目前，大部分模型假设多孔介质颗粒和水合物形态为规则形状，而实际中，不同种类的多孔介质颗粒拥有不同的形状和堆积形态，水合物在孔隙空间中的生成，呈现出随机离散和不规则性，理想的等径颗粒模型与现实状况存在一定差异。为了研究多孔介质堆积模式及水合物形态对渗透率测量过程的影响，首先以玻璃珠为多孔介质，在高压反应釜中原位合成甲烷水合物；其次，通过稳态注水测量含不同水合物饱和度的水相有效渗流率；最后，建立了簇状等径颗粒模型，揭示了水合物饱和度对多孔介质渗透率的影响规律。

1 实验

1.1 实验装置

图1所示为含水合物的多孔介质渗透率实验装置。由图1可见：高压反应釜垂直浸没在恒温水浴中，维持实验温度在8 ℃。反应釜的内径为20.0 mm，长度为250.0 mm。反应釜的进口端和出口端连接高精度差压传感器，用于在渗透率测量过程中实时测量反应釜两端的差压。反应釜从进口端面自下而上安装了3 个温度传感器和2 个压力传感器。储气罐有效容积为251.50 mL。平流泵提供稳定的高压液流，流量范围为0.1～50.0 mL/min。回压阀控制整个反应釜液路体系的压力保持在设定压力。高精度电子天平实时计量注入和产出的水的累计质量，从而得到渗透率测量过程的流速。气液分离器用于气水分离，排除气体对液体质量计量的影响。数据采集系统实时记录所有的压力、温度等，时间间隔设定为15 s。稳态注入的流体经过盘管冷却，消除注入热量而导致水合物分解的影响。

图1 含水合物的多孔介质渗透率实验装置[18]Fig.1 Schematic of apparatus for permeability measurements[18]

1.2 实验材料

使用的去离子水的电阻率为18.25 MΩ/cm。甲烷气体的纯度超过99.9%。玻璃珠选用BZ-02型玻璃珠，材质为钠钙玻璃。实验前，玻璃珠需要经多次去离子水清洗，并进行筛选烘干处理。玻璃珠的密度为2.495 g/cm3，粒径范围为109.0～479.0 μm，体积平均粒径为228.4 μm，区间体积分布和累计体积分布如图2所示。

图2 玻璃珠粒径分布图Fig.2 Particle size distribution of glass beads

1.3 实验步骤

1)孔隙度测量。将128.41 g玻璃珠填充至反应釜内，注水测量得到有效孔隙度φ为39.56%，其孔隙度与等径颗粒的斜方排列堆积方式的孔隙度(孔隙度为39.54%)[19]接近，玻璃珠堆积方式为斜方排列堆积。

2)查漏。将反应釜体接入实验管路，通过注入去离子水将管路的残余空气排出，持续2 h。将恒温水浴箱的温度调节到8.0 ℃，向反应釜注入甲烷气至出口压力达到20.0 MPa，将系统静置48 h以上，后期压力保持稳定不漏气，则反应釜体系不漏。

3)实验准备。实验系统检漏后，向反应釜注水，排出反应釜及连接管线的气体，而后关闭反应釜，打开反应釜上端的排空阀和注水端阀门，向反应釜内部注入少量甲烷气体，并排出一定量的水。

4)水合物生成。利用高压储气罐向反应器中注入高纯甲烷气体，并达到实验设定压力，封闭反应釜系统并静置一段时间。待反应釜内温度压力稳定后，利用平流泵向反应釜内注入去离子水，使得反应釜系统的出口压力达到20.0 MPa，关闭反应釜进出口阀门，直至水合物生成结束。水合物生成过程中，通过数据采集系统实时记录反应釜内的温度和压力，反应釜内的各相饱和度根据反应釜系统的压力和温度变化计算获得[13]。

5)水相有效渗透率测量。水合物生成结束后，采用稳态注水测定含不同水合物饱和度的多孔介质的渗透率，测量过程的回路压力高于水合物生成末期的压力。为保证渗透率测量时沉积物的流动状态为有效的稳态层流，注水速率控制在0.2～5.0 g/min，本实验的注水速率选择1.0 g/min。反应釜内的孔隙空间内还残余部分的自由气体，通过注入的去离子水驱替这部分自由气体，随后测量渗透率。采用差压传感器测量反应釜两端压差，高精度天平测量进水端和出水端的累积质量，从而计算注水流量和出水流量。

1.4 计算方法

含水合物的玻璃珠渗透率根据DARCY定律计算得到

式中：KW为水相渗透率，m2，Qavg为注入和流出反应釜的平均流量，m3/s；μw为水的动力黏度，Pa·s；L为反应釜内部有效长度，取0.25 m；A为反应釜内部有效横截面积，取3.14×10-4m2；ΔP为渗透率测量过程中反应釜进出口压差，kPa。当沉积物中没有水合物存在时，绝对渗透率常用K0表示，m2。渗透率比KrW为量纲一参数，即

2 实验结果

本研究以玻璃珠为多孔介质，通过多次注水法提高甲烷水合物的生成速率，并采用稳态注水法测量含不同水合物饱和度的玻璃珠的水相有效渗透率。表1所示为甲烷水合物生成、渗透率测量的实验数据，其中，系统压力为进出口端压力的平均值。

表1 甲烷水合物生成、渗透率测量的实验数据Table 1 Experimental data of methane hydrate formation and permeability measurement

2.1 水合物的生成

在水合物生成过程中，伴随着甲烷气体和水的消耗，釜内压力会逐步降低。水合物的生成一般持续12 h 以上，随着生成驱动力减小，水合物生成速率逐渐减慢。为达到实验所设定的水合物饱和度，采用多次注水增压的方法，维持反应釜内的压力保持在高位，提高水合物生成的驱动力。在水合物生成过程中，甲烷气体的摩尔体积根据反应釜内的系统压力和平均温度采用PENGROBINSON 气体状态方程得出，各相饱和度的变化通过质量守恒方程和甲烷气体的体积变化计算得到[13]。

图3所示为实验8水合物生成过程中的反应釜进/出端压力、水合物和气相饱和度随时间的变化。在第1次注水增压后，关闭反应釜，反应釜内初始气体饱和度为18.03%，初始液体饱和度为81.97%。从图3可见：在第1 阶段(0～1 173.0 min)，反应釜的系统压力从21.6 MPa 降低到16.6 MPa，水合物开始生成，反应釜体系内液相饱和度降低到76.01%，水合物饱和度达到7.32%，在后期压力下降趋势变得缓慢。第1阶段所出现的进口压力和出口压力出现不一致现象，这是生成的水合物堵塞进液管道造成的。随着多孔介质中水合物的生成和甲烷气体的不断消耗，反应釜内的进出口压力逐渐降低且其降低趋势逐渐变缓，表明水合物的生成速率逐渐下降。

图3 实验8中气相/水合物饱和度，进/出口压力和温度随时间的变化Fig.3 Gas/hydrate saturation,inlet/outlet pressure and temperature versus time in Test 8

利用平流泵进行第2次注水加压，向反应釜注水1.65 g，反应釜的系统压力到21.5 MPa，由于二次注水的时间较短(小于2 min)，水合物在注水阶段生成量可忽略不计。在第2阶段水合物生成持续2 389.9 min，液相饱和度从79.45%降低到77.19%，水合物饱和度增加到10.74%。第2 阶段后期水合物生成速率变得缓慢。

进行第3 阶段注水加压，向反应釜注入0.63 g水，水合物进一步生成。在水合物生成结束时(t=4 000.0 min)，反应釜内三相饱和度为SW=76.65%，SG=9.74%，SH=13.61%。实验结果表明，甲烷水合物的生成速率随着反应釜压力下降会显著降低，采用多次注水增压的水合物生成方法，可以有效提高反应釜体系的水合物生成速率。

2.2 渗透率测量

图4所示为实验8中的累计进水/出水量和反应釜平均温度。由图4可见：注水前，去离子水先预冷到8.0 ℃，再经冷却盘管使得注入的液体温度与反应釜的保持一致。在图4中，进口注水速率Qin为0.986 0 g/min、出口产水速率Qout为0.975 0 g/min，注水和产水速率的线性相关系数R2均大于0.999 9，表明稳态注水测量过程中去离子水流速稳定，且反应釜内为液体的单相流动。

图4 实验8中累计进水/出水量和平均温度Fig.4 Accumulated water mass of injection/production and average temperature in Test 8

图5所示为实验8中的进/出口压力、压差以及渗透率特征。渗透率测量过程中，反应釜体系的压力始终维持在15.0 MPa，主要分为2个阶段。在第1阶段，随着稳态注水过程，反应釜两端差压从0 kPa 逐步增大到150.0 kPa，这一阶段为残余气体的排出阶段[20]，反应釜体系的水饱和度不断增大，直至排出所有残余气体。水合物会阻塞多孔介质的孔隙通道，从而影响气液流动通道。在第2 阶段，随着稳态注水过程，差压波动较小，能够维持相对较长时间的稳定(90 min以上)，反应釜两端差压保持稳定一段时间，表明这一阶段体系的各相饱和度保持稳定，其平均差压为145.8 kPa，根据Darcy定律计算的渗透率为0.121×10-12m2，相关数据如表1所示。

图5 实验8中的进/出口压力以及渗透率特征Fig.5 Characteristic of pressure of injection/production and water effective permeability in Test 8

3 讨论

3.1 簇状等径颗粒模型

考虑水合物存在时，颗粒模型常被作为渗透率预测中多孔介质的物理模型，KLEINBERG等[11]总结了等径颗粒模型和SPANGENBERG 模型，简化渗透率比和水合物饱和度之间关系式，

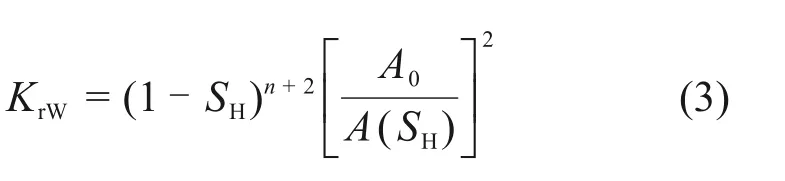
式中：A0为不存在水合物时孔隙内表面积，m2；A(SH)为存在水合物时孔隙内表面积，m2，n为ARCHIE饱和度指数，表征水合物饱和度对流体在多孔介质中流动的迂曲度与孔隙度之间的影响。在颗粒模型中，假定沉积物颗粒为理想等径球体，而水合物的形态具有不规则性。KLEINBERG等[11]引用了水合物生成前后的形状因子f(SH)，简化了多孔介质和水合物的形态变化对渗透率的影响，对于等径颗粒模型，f(SH)=1，其适应于理想等径球状堆积物的渗透率预测。当n大于1时，n越大，其水合物饱和度变化对流体在多孔介质流动影响越剧烈。n导致等径颗粒模型更具有适用性和灵活性。多数含水合物的多孔介质渗透率模型聚焦在多孔介质的堆积方式和水合物颗粒的赋存形态。

图6所示为多孔介质堆积模式与水合物颗粒占据孔隙中心示意图。由图6可见：对于多孔介质的堆积模式，图6(a)和(b)为简单立方堆积[13-14]，图6(c)和(d)为斜方排列立方堆积[15,19]。现实的水合物在孔隙空间中的赋存形态通常表现为不规则形状的水合物簇团[21]，本文考虑了多孔介质颗粒的堆积状态和水合物赋存状态，提出了簇状等径颗粒模型，如图6(d)所示。

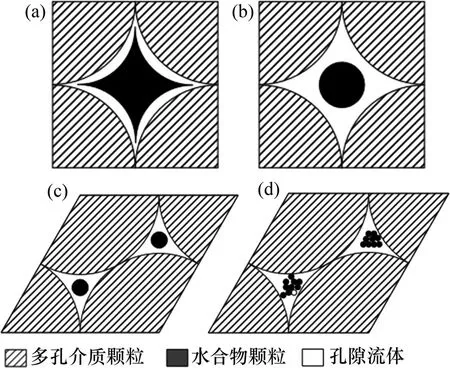
图6 多孔介质堆积模式与水合物颗粒占据孔隙中心示意图Fig.6 Schematic diagram of accumulation mode of porous media and pore center occupied by hydrate particles

簇状等径颗粒模型进行如下假设：

1)多孔介质颗粒为斜方排列堆积模式的等径球体；

2)所有水合物颗粒表面光滑；

3)水合物球状颗粒成簇团状，以点接触形式连接在一起，其形态是灵活多样，在水合物渗透率测量过程中不发生分解或移动。

水合物饱和度增大会伴随着水合物颗粒增多，增加的水合物颗粒聚集成簇，颗粒之间具有一定的生长界限。将反应釜内部的整体多孔介质体系为研究对象，在簇状等径颗粒模型中，存在水合物时，多孔介质的总孔隙内表面积A(SH)表示为

式中：nh为多孔介质体系的水合物颗粒总数目；Ah为单个水合物颗粒的表面积，m2。

式中：VH为反应釜内部的水合物颗粒总体积，m3；Vh为单个水合物颗粒的体积，m3；Dh为单个水合物颗粒的直径，μm。对于单个水合物颗粒的尺寸，KIM 等[22]在所有水合物颗粒尺寸相同的假设基础上，提出了一个甲烷水合物的分解动力学模型，并根据实验数据拟合推算出甲烷水合物颗粒直径为16.0 μm。CLARKE 等[23]在KIM 实验思路的基础上，使用粒度分析仪观测到甲烷水合物颗粒的直径大致为8.0 μm，标准偏差约为3 μm。本文选用8.0 μm作为甲烷水合物颗粒直径，即Dh=8 μm。水合物颗粒在孔隙中的总体积VH表示为

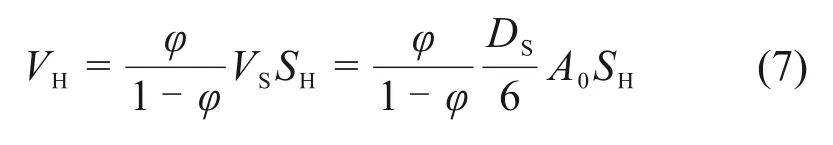
式中：VS为反应釜内部的多孔介质颗粒的总体积，m3；有效孔隙度φ为39.56%；DS为单个多孔介质颗粒的直径，μm。BZ-02 型玻璃珠的体积平均粒径通过粒径分析仪测量获得，DS=228.4 μm；综合式(4)～(7)，孔隙内表面积A(SH)可表示为

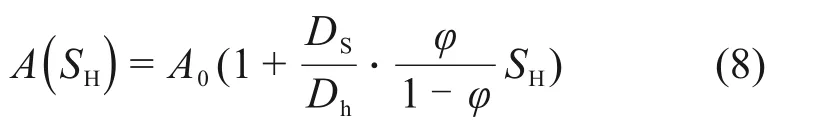
为描述水合物的存在对渗透率的影响，将式(8)代入式(3)中，渗透率比KrW可表示为

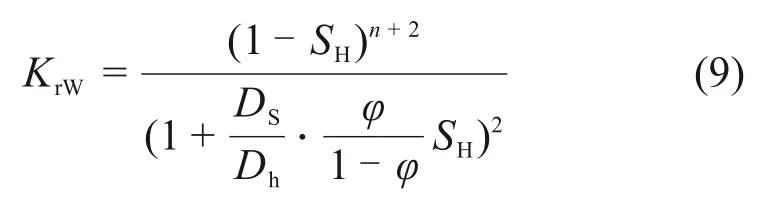
3.2 实验结果与模型的对比

图7所示为实验结果与4 个渗透率模型的关系。由图7可见：即使在较低水合物饱和度情况下，随着水合物的饱和度增加，多孔介质实验测量的渗透率逐渐减小，含水合物的玻璃珠渗透率比KrW下降速率变快，即使较低水合物饱和度也会导致较小渗透率。在玻璃珠和水合物粒径测量的基础上，本文提出了簇状等径颗粒模型，当ARCHIE饱和度指数n为10时，该模型与实验数据吻合较好。从图7可以看出，含水合物多孔介质的渗透率比KrW与水合物饱和度之间呈指数递减关系。相较其余3 个模型(n=35)，在相同水合物饱和度下，簇状等径颗粒模型的孔隙内表面积A(SH)更大，这表明流体在多孔介质流动时与颗粒间的接触摩擦面更大，从而影响气液渗流过程。

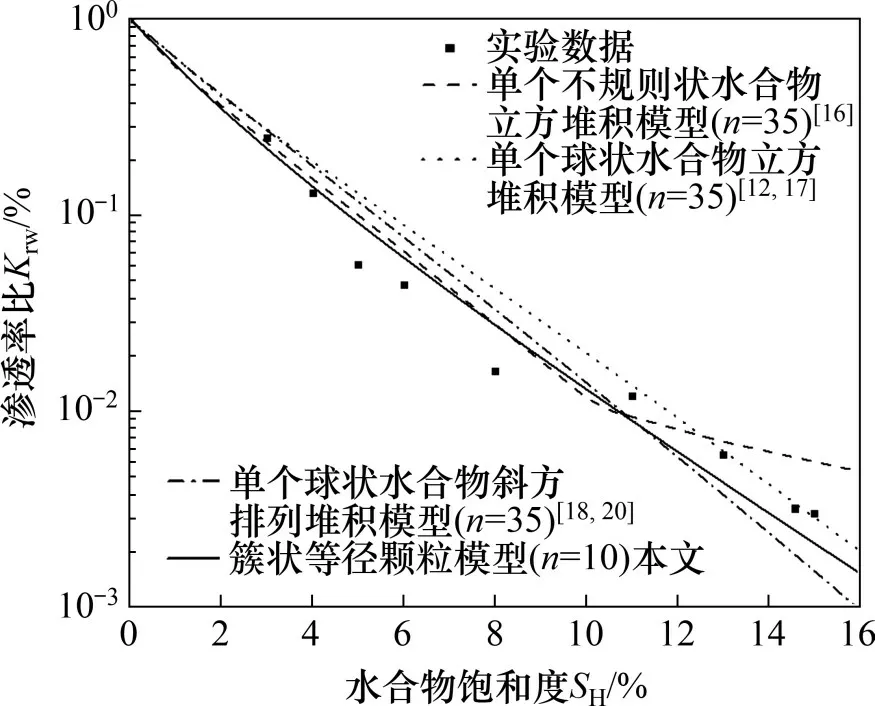
图7 实验结果与渗透率模型的关系Fig.7 Relationship between experimental results and permeability model

水合物对多孔介质渗透率有2 个方面的影响：1)水合物颗粒占据孔隙空间从而阻塞流动通道，水合物饱和度越大，流体流动的有效孔隙空间越小；2)流体流动的接触摩擦面随着水合物饱和度增大而增大，在相同的驱动压差下，摩擦阻力也会更大。因此，水合物饱和度越大，其对多孔介质渗透率的影响越显著。

4 结论

1)实验采用球形较好的BZ-02 型玻璃珠为多孔介质，玻璃珠的堆积形式符合等径球体颗粒的斜方排列堆积的理论孔隙度；采用多次注水增压的甲烷水合物生成方法，可有效提高反应釜体系的水合物生成速率；在稳态注水渗透率测量过程中，反应釜体系的渗透率KW先减小而后维持稳定。

2)在等径颗粒模型的基础上，簇状等径颗粒模型假设水合物颗粒为等径球状颗粒，水合物颗粒成簇团状分布在孔隙空间中，其孔隙空间的内表面积A(SH)随着水合物饱和度增大而增大。

3)实验所选用的玻璃珠更符合等径颗粒模型的假设条件，当ARCHIE 饱和度指数n为10 时，簇状等径颗粒模型与实验数值吻合较好，在低水合物饱和度(0～15%)下，含水合物多孔介质的渗透率比KrW随水合物饱和度增大而呈指数递减。