Beating standard quantum limit via two-axis magnetic susceptibility measurement

Zheng-An Wang(王正安) Yi Peng(彭益) Dapeng Yu(俞大鹏) and Heng Fan(范桁)

1Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China

2School of Physical Sciences,University of Chinese Academy of Sciences,Beijing 100190,China

3Shenzhen Insititute for Quantum Science and Engineering,Southern University of Science and Technology,Shenzhen 518055,China

4Guangdong Provincial Key Laboratory of Quantum Science and Engineering,Southern University of Science and Technology,Shenzhen 518055,China

5Shenzhen Key Laboratory of Quantum Science and Engineering,Southern University of Science and Technology,Shenzhen 518055,China

6CAS Center for Excellence in Topological Quantum Computation,University of Chinese Academy of Sciences,Beijing 100190,China

7Songshan Lake Materials Laboratory,Dongguan 523808,China

Keywords: quantum metrology,spin-squeezing,standard quantum limit,fluctuation

1. Introduction

It has attracted plenty of attention in the endeavor to suppress the fluctuation of ˆJnand improve the single-atom resolution.[21,22]Others have worked to circumvent the singleatom resolution requirement.The main idea is to use nonlinear atomic interaction to suppress the fluctuation of ˆJn, which is the so-called echo procedure. The echo procedure can utilize the same nonlinear interaction which is employed to generate multipartite entanglement at the first stage.[23-26]We find that measuring magnetic susceptibilities along two mutually orthogonal axes perpendicular to parameter fieldφcan produce parameter estimation precision beyond SQL.The importance of our work is two-fold. Firstly, it shows that neither single-atom resolution nor nonlinear interaction is necessary on final measurement stage of metrology to achieve precision improvement beyond SQL.Secondly,it employs the most convenient measurement and is robust to detection errors. Thus,it is one step further to achieve metrology gain beyond SQL promised by quantum mechanics in practice.

2. One-axis spin squeezing

We consider an atomic ensemble consisting ofNatoms.They are firstly initialized to the coherent spin state along thexdirection. We then use the one-axis spin squeezing Hamiltonian ˆJ2zto generate multipartite entanglement among the atoms. Following the standard procedure of one-axis spin squeezing,a little adjustment along thexdirection would also be implemented[27,28]

Fig.1. Quasiprobability and magnetic susceptibility. The quasiprobability P(θ,φ)=|〈θ,φ|ψ〉|2 has been calculated for spin ensemble with N =100 spins. |θ,φ〉is the coherent spin state where all the spins pointing along the direction with polar angle θ and azimuth angle φ. The distribution of the quasiprobability is of similar shape for other values of N. The only difference is that the quasiprobability would be more concentrated as the number of spins grows larger. (a) The coherent spin state is initialized along the positive x direction. (b) The one-axis spin squeezed state. (c) The one-axis spin squeezed state rotates along the y axis clockwise through an angle φ. (d)Normalized magnetic susceptibility〈ˆJφ〉/N. The blue solid line describes the atomic ensemble initialized in an one-axis spin squeezed state. When the initial spin squeezed state rotates along the y axis through an angle φ,the curve would be shifted toward right by φ (orange dashed line). Note that〈Jφ〉is cyclic functions of φ and N=1000 here.

3. Interference procedure

The atomic spins would be sent through a magnetic field pointing to the positiveydirection. Let us assume that the overall quantum channel is ˆUφ= e-iφˆJy. The output state of the atomic ensemble is

Measuring the atomic ensemble coming out of the magnetic field, we expect to estimate the value ofφand thus the value of the magnetic field.

4. Magnetic susceptibility measurements along two directions

It is widely believed that there is always an optimal measurement for a particular metrology scheme. In many cases,it can be proven that such kind of optimal measurement exists.[6]Others believe that adaptive feedback measurement can give the optimal information extraction.[16-20]Most of these measurement procedures are too complex to be realized on atomic ensembles. Magnetic susceptibility measurement is easy to be carried out on atomic ensembles.In most cases,it is not an optimal measurement scheme. Our goal here is to use the most simple measurement to achieve as high metrology precision as possible.

There is only one single peak of the〈ˆJφ〉curve which is located atφ=π/2. When the atomic ensemble initialized in a one-axis spin squeezed state comes out of the ˆUφchannel,the peak of the〈ˆJφ〉curve would shift byφ.〈ˆJφ〉would be maximum if and only ifφ=φ+π/2,

4.1. Performance analysis

Fig. 2. Performance of the two-axis magnetic susceptibility measurement scheme for estimating φ. (a) Scaling of the imprecision Δφ versus atomic ensemble size N. (b) The optimal squeezing time ts for different atomic ensemble size N. (c) The imprecision Δφ given by 1000 atomic spins with different squeezing time. There is a single valley of the Δφ versus ts curve and the corresponding optimal squeezing time(marked red star)is employed in our scheme. (d)Fisher information of one-axis spin squeezed state given optimized squeezing time as shown in(b).

We have simulated our metrology scheme for up to 2480 atomic spins.R=2 magnetic susceptibility measurements are carried out for estimating eachφ, of which one is along thexaxis and the other along thezaxis. Thus, we have two experiments employing the same atomic ensemble, which goes through the same initialization and interference procedures plus a final magnetic susceptibility measurement at the end.The only difference is along which(xorz)direction the magnetic susceptibility measurement is carried out. The results of the two measurements are submitted to Eq.(6)to produce an estimationφestofφ. For each randomly chosenφ, we obtain its estimationφestbyR=2 experiments. Note thatφis fixed in these two experiments. We repeat the estimationM=1000 times for differentφbetween 0 and 2πto evaluate Δφin the entire range of values,

As shown in Fig. 2(a), our two-axis magnetic susceptibility measurement scheme can produce parameter estimation with imprecision below standard quantum limit forN16.The scaling Δφwith respect to the atomic ensemble size is

The optimaltsis around the value of 0.4/N2/3as shown in Fig. 2(b). Given the optimized squeezing timets, quantum Fisher informationFof the corresponding one-axis spin squeezed state scalesF=0.833N1.42with respect toN. It matches the scaling of (Δφ)2with respect toN, c.f., Eq. (8).The consistency of our numerical results obtained from different approaches confirms that they are valid and reliable. We must emphasis thattsis optimized to obtain the highest estimation precision given by Eq.(6)instead of the highest quantum Fisher information. Note that the quantum Fisher information is[6]

4.2. Robustness to detection noise

Further, we have investigated the robustness of our metrology scheme against the detection noise. The noise has two possible origins: a) defects of the detection apparatus and b) spin fluctuation agitated by surrounding environment.When measuring ˆJz,we are actually counting how many atoms are occupying the spin up state|↑〉. A defected detector would give usn↑+Δnin one counting, when it should ben↑if the detector is perfect. On the other hand,the environment would agitate a portionpNout of the totalNatoms to flip.

Table 1. Scaling α of the imprecision Δφ with respect to N. α is calculated by fitting Δφ ∝1/Nα. σ is measurement fluctuation induced by environment noise and measurement defects.

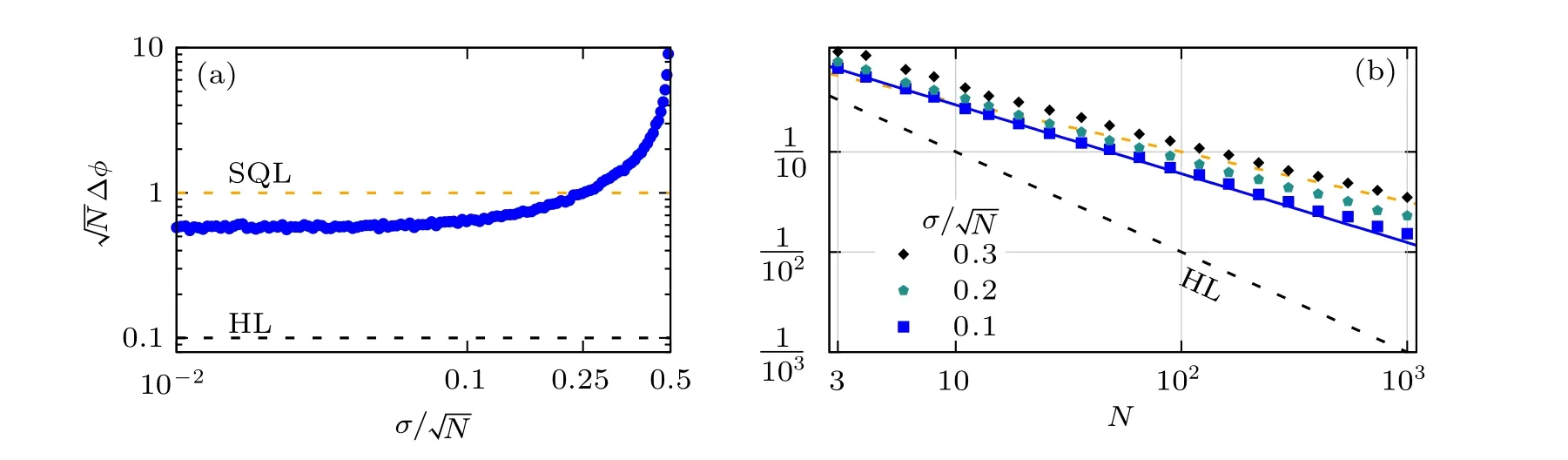
Fig.3. Robustness against detection errors. The dashed orange line corresponds to SQL while the dashed black line to HL.(a)Imprecision Δφ versus fluctuation σ induced by environment noise and measurement defects,given N=100. (b)Scaling of Δφ against different level of the detection defects and environment noise induced measurement fluctuation σ =0.1N,0.2N,0.3N. The solid blue line is the imprecision scale in the noiseless case as shown in Fig.2(a).

5. Summary and outlooks

Acknowledgments

This work was supported by the National Natural Science Foundation of China(Grant Nos. T2121001,11934018,and U1801661), Strategic Priority Research Program of Chinese Academy of Sciences (Grant No. XDB28000000), the Key-Area Research and Development Program of GuangDong Province, China (Grant No. 2018B030326001), Guangdong Provincial Key Laboratory(Grant No.2019B121203002),the Science,Technology and Innovation Commission of Shenzhen Municipality (Grant Nos. KYTDPT20181011104202253 and 2016ZT06D348).