Quantum walk search algorithm for multi-objective searching with iteration auto-controlling on hypercube

Yao-Yao Jiang(姜瑶瑶) Peng-Cheng Chu(初鹏程) Wen-Bin Zhang(张文彬) and Hong-Yang Ma(马鸿洋)

1School of Science,Qingdao University of Technology,Qingdao 266033,China

2School of Information and Control Engineering,Qingdao University of Technology,Qingdao 266033,China

Keywords: multi-objective,quantum walk,search algorithm,accurate probability

1. Introduction

Quantum computing is an emerging computer science and technology in recent years. In the past two decades, this subject has developed rapidly both on theoretically and experimentally, and has become an international research hot spot,with a series of breakthrough research results.[1]Moreover,quantum computing can process the eigenstates of superposition state in parallel. So quantum algorithm has quadratic and exponential advantages over classical algorithm. The research of quantum algorithm has profound theoretical significance and broad application prospect.[2]In 1996, Grover proposed a high performance quantum search algorithm for unstructured databases, which has quadratic property than any possible classical algorithm.[3]Grover search algorithm is formed by repeated application ofUoperator. The number of iterations in the whole process directly affects the probability of output target state. Since then, quantum search algorithms have be continued to study.[4-6]Furthermore quantum walk is a branch of quantum computing,and it is the counterpart of the classical random walk in the field of quantum mechanics.Quantum walk has the generality and the advantage of parallel computation of quantum algorithm. Therefore, scholars have carried out a series of researches and applications using quantum walk,[7-10]and a lot of search algorithms based on quantum walk are proposed. In 2003,Shenvi,Kempe,and Whaley proposed a quantum algorithm based on quantum walk (This algorithm is called the SKW algorithm). The SKW search algorithm can be used to find hypercube vertices marked by Oracle.[11]In 2009,by examiningnneighbors of the measured results,Potoeket al.greatly optimized the probability of finding a solution based on search results,and increased the probability of finding a solution to close to 1.[12]Besides,in the last part of the literature,an improved scheme based on the original SKW algorithm is proposed,but its correctness is not proved.In 2014,Zhuet al.designed a new algorithm to automatically control the iterative process by adding a phase detection. In the case that the number of target states is unknown, when the operator just iterates to the maximum amplitude of the target state,the algorithm can be stopped automatically.[13]Since search algorithms and algorithms that can be transformed into search problems have a wide range of applicability,after these pioneering articles,scholars have conducted in-depth research.In China, Long[14]constantly improve Grover search algorithm;Sheng,[15-17]Zhouet al.[18-21]also in the field of quantum search algorithm and quantum computing have made efforts.

Although the scholar gate has done a lot of work on the quantum walk search algorithm, when searching for multitarget state,the quantum search algorithm still has the problem of many iterations and low precision,which leads to the inefficient search algorithm in the application.Therefore,the design of the multi-target search algorithm for quantum wandering is still a problem, especially when the number of unknown target states is unknown. Based on this problem, an unknown number of target states search algorithm based on quantum walk is designed. In this paper,by modifying the search algorithm of multi-objective states in the following two aspects,an automatic search algorithm based on quantum walking is proposed in the case of multi-objective state positions.Firstly,the iterative process is automatically controlled by adding phase detection gate(the operationPfor short), in order to find the optimal number of iterations of quantum walk. Because in the quantum walk process, iterative operators have a cyclical effect on any system state,that is,the role of iterative operators is not convergent. If the number of iterations is less or more than the optimal number, the probability of eventually reaching the target state is reduced,so we need to stop the algorithm the first time the magnitude of the target state becomes maximum. The optimal number of iterations at this point reduces unnecessary iterations while ensuring that the target state is measured, in other words, the algorithm effectively reduces time complexity. Secondly,by decomposing the Hilbert space where the search space is located into the direct sum of several disjoint subsets,the goal is to increase the accuracy of the search to the target state. Since the accuracy of searching for a single target state has reached 1,the purpose of decomposing the Hilbert space into several dissection subsets of straight sum is to convert the projection measurement of the target state of the multipart into the measurement of the single target state,so that the accuracy of the search for the multi-target state is also greater than 90%. The controllable quantum walk search algorithm has the characteristics of less iteration times, high efficiency and high accuracy in searching the target state.

The paper is organized as follows. In Section 2,the SKW search algorithm and the multi-objective coin operator are introduced. In Section 3,the composition of the new algorithm and the process of searching the algorithm is described. In Section 4, the SKW search algorithm is compared with the controllable quantum walk search algorithm in terms of time complexity and accurate probability of searching the target node. In Section 5, the advantages of the improved search algorithm are obtained and the results are summarized.

2. Background

The SKW algorithm uses Grover walk as the basic algorithm framework and will be based on quantum walk on thencube. The hypercube is a graph withN=2nnodes withndimensions,in which each point can be marked with ann-bit binary string. Two nodes described asxandyon the hypercube. If|x-y|=1, two nodes are connected by an edge,where|x| is the hamming weight ofx. So the Hilbert space of the search algorithm can be writtenH=Hn ⊗H2n. Each state ofHcan be defined as a bit stringxrepresenting the position on the hypercube,and each state ofHcan be defined as a directiondrepresenting the state of the coin space. The shift operatorSmaps a state|d,x〉to the state|d,x ⊕ed〉, whereedis thed-th basis vector on the hypercube. ThenScan be expressed as

In the SKW quantum search algorithm,C0is selected as an N-dimensional Grover operator,andC1is selected asI.Because of the symmetry of hypercube graphs,vertices can be relabeled in such a way that the labeled vertices becomextg=0.Then the initial state is

3. Improvement of algorithm

3.1. Composition of the algorithm

Now we consider the optimization of the quantum walk search algorithm when the number of target states is greater than 1. To formalize the task of finding multiple marked vertices.LetHidenote the subspace spanned by states|d,x〉such that|x|meet the condition:|x|=|x|⊕i,i=1,2,...,n. TheHiisi-th subspace ofH,and meets

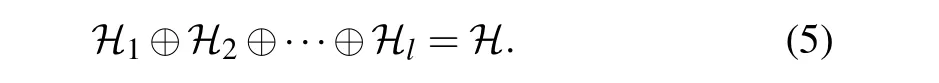
The subspaceHirefer to a sign where the target vertex is denoted byxtg=0.

In addition,it was found that when the phase of the superposition state became negative for the first time,the amplitude value of the search target reached its maximum, and the positivity and negativity of the phase in front of the|++···+〉component based onXdetermined the positivity and negativity of the phase of the superposition state in the paper.[13]Therefore, the phase detection gate can be used to estimate the positive and negative phase. The position where the detection gate moves in should be behind the Oracle operator, that is,when the Oracle operator is applied,the amplitude value of the target component is the largest when the phase and the first negative change. The Oracle operator of quantum walk search algorithm based on complete graph is in the coin operator. So,intuitively, the Phase operator should be embedded intoC＇m,that is,the new quantum walk coin operator should be set as

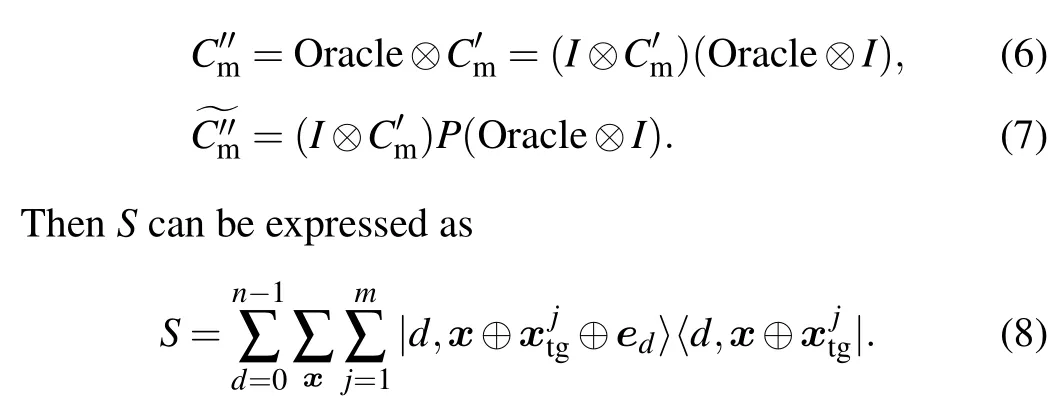
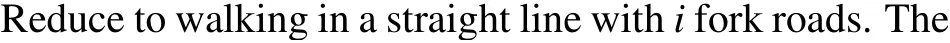
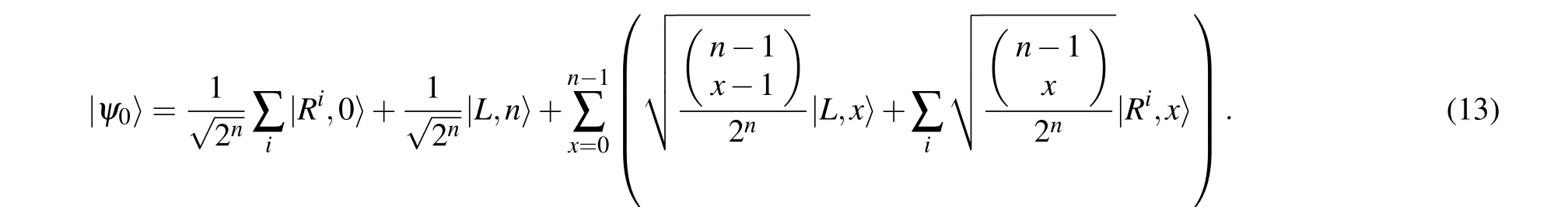
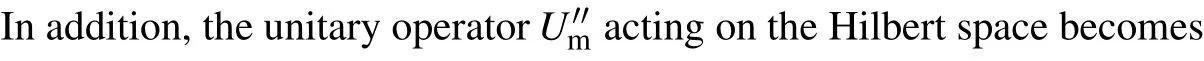
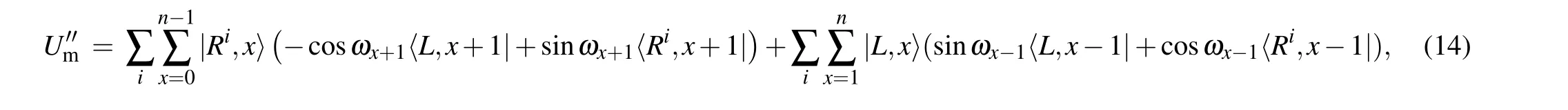
3.2. The decision process of P operator

The determination ofPoperator when the amplitude of element connection of groupsiare about to reach the maximum value is analyzed in detail as follows:

(i) When the amplitude value of the result of the groupi=1 elements|x|does not reach the maximum value through the next mean inversion operator, the groupsi=2,3,...elements|x|is acted on by the Oracle operator. In this case,thePoperator does not stop the algorithm because elements can make the phase sum negative.

(ii) It is assumed that the amplitude of the result of the groupi=2 elements|x|has reached the maximum value,and the Oracle operator is applied,but the groupsi=1,3,...elements|x|has not passed the mean inversion operator and does not reach the maximum value. But the phase sum of the groupi=2 elements|x| is already negative, and the phase sum of the groupsi=1,3,...elements|x| is positive and close to 0. Therefore, the joint phase sum of groupsi=1,2,3,...elements may be positive or negative, that is, there is a certain probability that the algorithm will stop in this iteration.

(iii)In the next iteration, when the solution of the groupi=1 elements|x|has reached its maximum value,the Oracle operator is applied. At this time,the phase sum of the groupsi=2,3,...elements and the groupi=1 elements is negative,so the algorithm must be stopped in this iteration.

In summary,when thePoperator stops the algorithm,the results of groupielements can be measured with a certain probability. However,no matter which group is measured,the maximum amplitude of the element solution can be guaranteed. The circuit diagram is shown below in Fig.1.

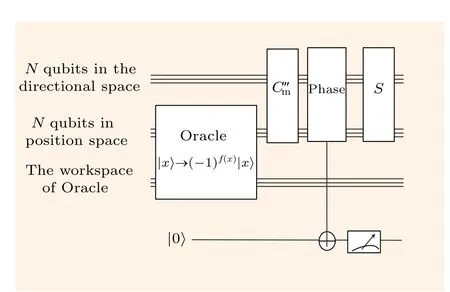
Fig.1. Quantum circuit diagram of search algorithm. As figure 1 shows that in every iteration of the U＇＇m operator,measure the constant bit after performing phase detecting gate. If the projection measurement of the state is |0〉,then the algorithm continues. If the projection measurement of the state is|1〉,the algorithm stops.

3.3. The algorithm process

(I) The initial state is effectively implemented in node space by applyingnbit Hadamard operations to state|0〉. A similar process applies to directional space.

(II)Cycle the following process. The operator is applied to the system state, and the auxiliary bit of measurement is:if the measurement result is|0〉, the cycle is continued; if the measurement result is|1〉,the cycle is ended.

(III)Measure the directional space state.

(IV)End of the algorithm.

4. Analysis of algorithm

4.1. Analysis of success rate of algorithm

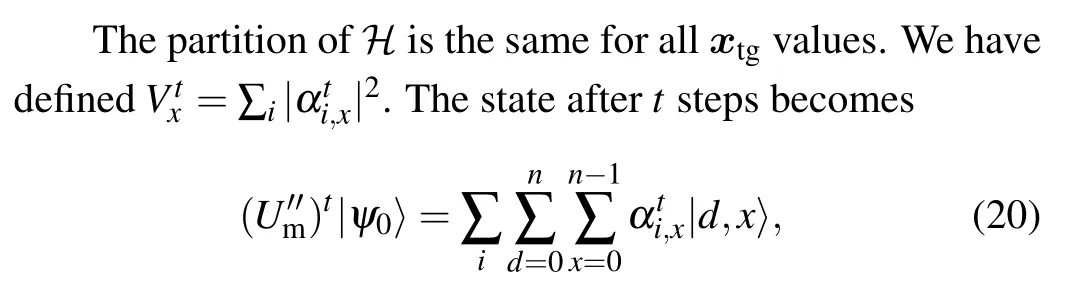
The property(23)can also be tested on the numerical results presented in Fig.2.

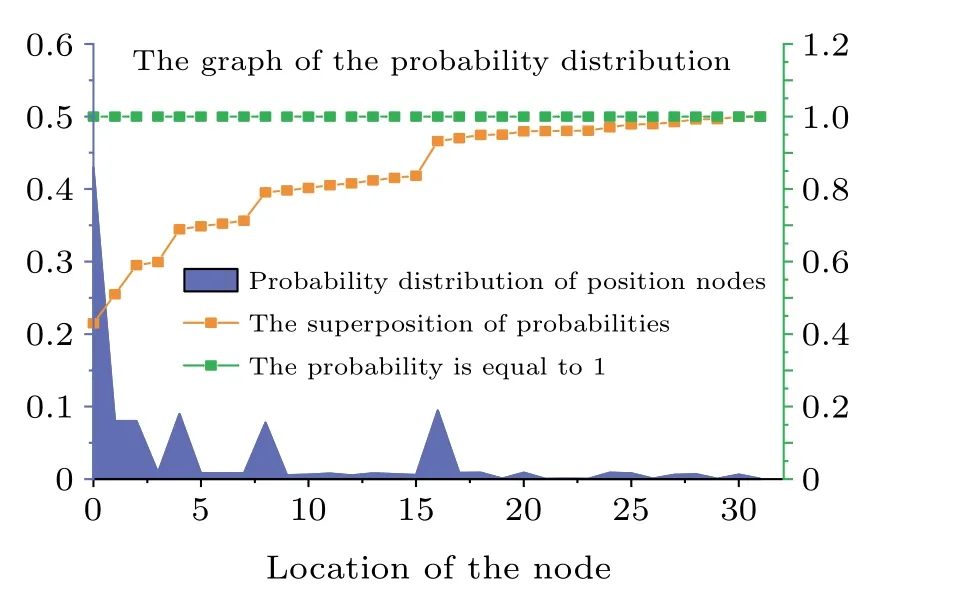
Fig. 2. The graph of the probability distribution. The plot shows the numerical probability distribution of node position after the optimal number of iterations. In accordance with the analytic results, the probability distribution has its maximum for the marked vertex xtg=0(the blue area)reaching a value close to 0.5. In addition,it can also be observed from the graph that nodes near the target node also have high probabilities and the sum of these probabilities(yellow curve)can be compared with the probability of the target node(refer to the axis on the right).

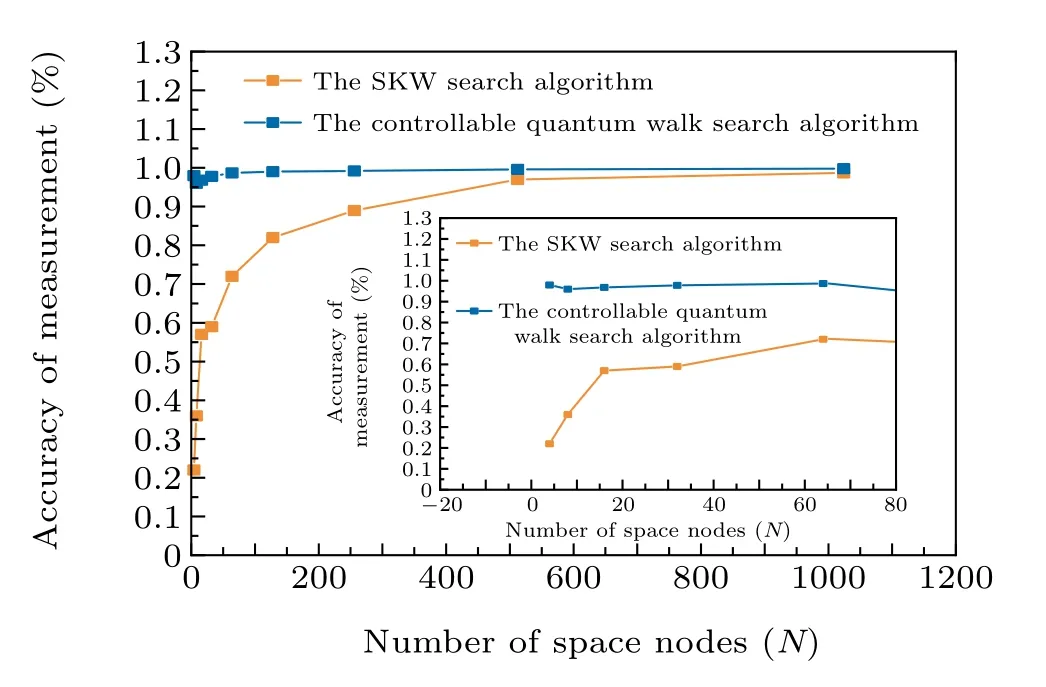
Fig.3. Comparison of measurement accuracy of two search algorithms. Figure 3 shows the variation trend of the accuracy of the two search algorithms to search the target state with the increase of the number of space nodes. For the controllable quantum walk search(blue curve),the accuracy of searching the target node is basically stable at about 90%as the number of space nodes increases.For the SKW search algorithm(yellow curve),with the increase of the number of space nodes,the accuracy of searching the target node is constantly increasing. This shows that only when the number of spatial nodes is large enough, can the SKW search algorithm search the target state more accurately. This also illustrates a limitation of the SKW search algorithm.

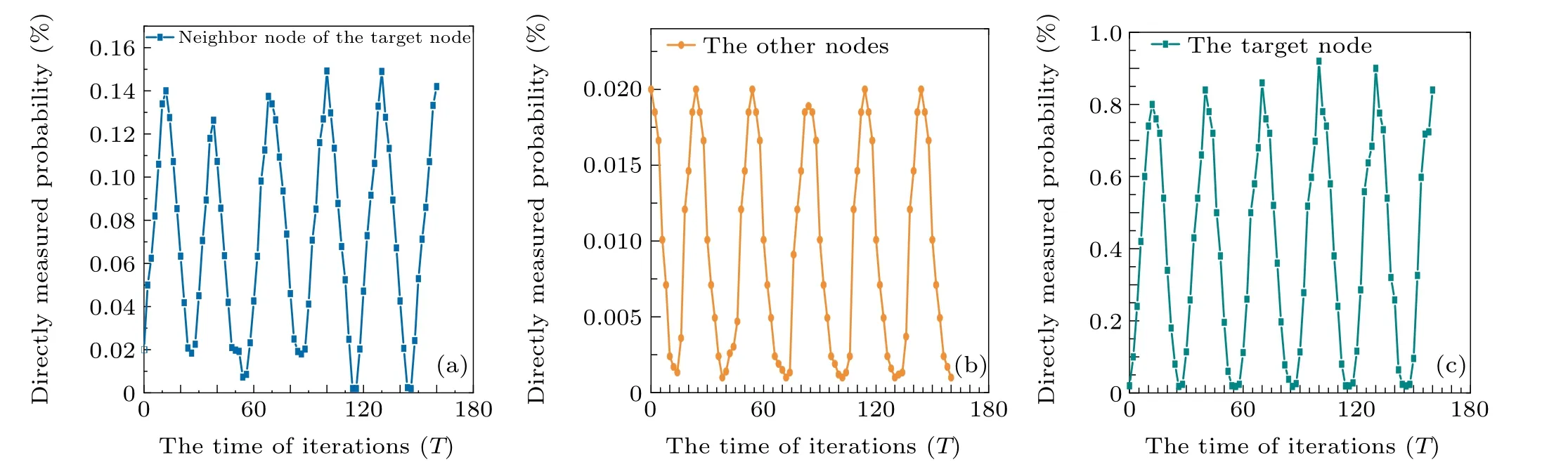
Fig.4. The probability distribution of different nodes. Figure 4 shows us the variation trend chart of the probability of directly measuring nodes of different classes in space as the number of iterations increases, where the blue line represents the neighbor nodes of the target node, the yellow line represents other nodes,and the green line represents the target node. The following results can be obtained from the figure: The increase of the number of iterations does not simply increase or decrease the measurement probability of different types of nodes, but there is an optimal number of iterations. If the optimal number of iterations can be calculated,the target node can be measured with a probability of 90%.

Therefore,since we havep0=(1/2)-O(1/n),the total probability of measuring the target nodes or any of its direct neighbors is

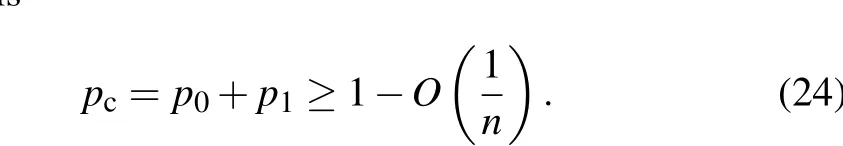
Since the upper bounded ofpcis 1,the total probability must be approachingpc=1 when n is large.Figure 3 is obtained by comparing the accuracy of the quantum walk search algorithm and the SKW search algorithm.

Therefore, if a complete projection measurement of the coin’s state is made, the marker element can be determined with the 1-O(1/n) probability after performing a quantum walk search. The projection measurement of the system state after substituting the operator method for an appropriate number of times will make the final probability of getting the target node higher than 90%.

Finally,we analyze the influence of the operatorPadded on the controllable quantum walk search algorithm in this paper. Figure 4 is the probability distribution of different nodes in the search space is obtained by using the controllable quantum walk search algorithm.

In other words,the operatorPadded in this paper can stop the algorithm directly when the optimal probability is reached for the first time,that is,the optimal iteration. In this way,the target state can be measured with an absolutely high probability (90%), and the optimal iteration number can be achieved,which can improve the search efficiency.

4.2. Analysis of the time complexity of the algorithm

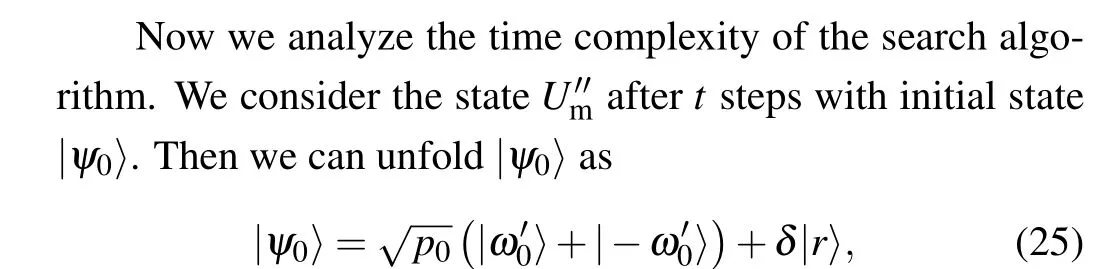
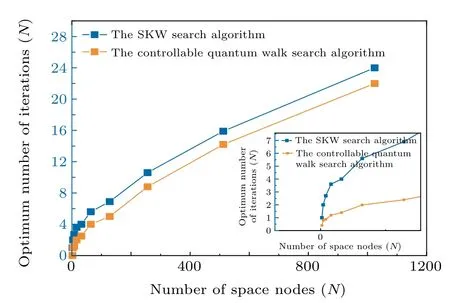
Fig.5. The comparing the the time complexity of two search algorithms.The figure shows the trend that the time complexity of the two search algorithms changes as the number of space nodes increases. It can be seen from the figure that the time complexity of SKW search algorithm is greater than that of the controllable quantum walk search algorithm. In other words,the controlled quantum walk search algorithm can search the target state at a high rate.

5. Conclusion

Acknowledgments

Project supported by the National Natural Science Foundation of China (Grant Nos. 11975132 and 61772295), the Natural Science Foundation of Shandong Province, China(Grant No. ZR2019YQ01), and the Project of Shandong Provincial Higher Educational Science and Technology Program,China(Grant No.J18KZ012). Thanks to Chen Zhenyu,Yan Dandan, and Ma Yulin for their help in the numerical simulation experiment. Special thanks to the scholars who have made important contributions in quantum computing and quantum search algorithm.