GLEASON’S PROBLEM ON THE SPACE Fp,q,s(B) IN Cn*

Pengcheng TANG (唐鹏程) Xuejun ZHANG (张学军)

College of Mathematics and Statistics,Hunan Normal University,Changsha 410081,China

E-mail: 1228928716@qq.com;xuejunttt@263.net

Abstract Let Ω be a domain in Cn and let Y be a function space on Ω.If a ∈Ω and g ∈Y with g(a)=0,do there exist functions f1,f2,···,fn ∈Y such that This is Gleason’s problem.In this paper,we prove that Gleason’s problem is solvable on the boundary general function space Fp,q,s(B) in the unit ball B of Cn.

Key words boundary general function space;Gleason’s problem;solvability;unit ball

1 Introduction

Letα=(α1,α2,···,αn) be a multi-index,where eachαlis a nonnegative integer.In this paper,the following abbreviated notations will be used: |α|=α1+α2+··· +αn,α!=

For any pointz∈B-{0},the involution automorphisms ofBare defined by

such thatφz(0)=z,φz(z)=0 andOtherwise,we defineφ0(w)=-w.

In this paper,the notation “EF” means that there exist two constantsa ＞0 andb ＞0 such thataF≤E≤bF.If there exists a constanta ＞0 such thatG≤aH(G≥aH),then we denote it by “GH” (“G≿H”).

Fors≥0,p ＞0,q+n ＞-1 andq+s ＞-1,the spaceF(p,q,s),which we call the general function space,consists off∈H(B) and

where the complex gradient offis defined by

In [1],we proved that

In [2],Zhao Ruhan first introduced theF(p,q,s) space on the unit disk.Later,many function spaces associated withF(p,q,s) were studied in various domains;see,for example,[1,3–11].In the definition of theF(p,q,s) space,the integral is on the unit ballBor the other domain Ω,for example,a bounded symmetric domain.In this paper,we will consider the corresponding function space of an integral on the unit sphere∂B,which we write asFp,q,s(B).

Definition 1.1Fors≥0,p ＞0,q+s≥0 andq+n≥0,the functionf∈H(B) is said to belong to the boundary general function spaceFp,q,s(B) if

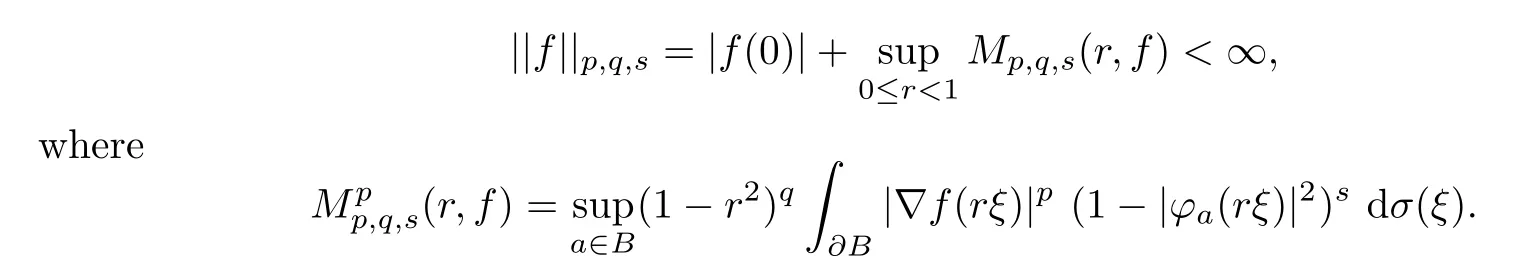
It is easy to prove thatFp,q,s(B) is a Banach space under the norm ||.||p,q,swhenp≥1,and theFp,q,s(B) is also a complete distance space under the distanced(a,b)=||a-b||pp,q,swhen 0＜p ＜1.We may also consider many properties ofFp,q,s(B).Gleason’s problem is one of these properties.

LetYbe a holomorphic function space on the domain Ω ⊂Cn.Gleason’s problem onYis the following: ifa∈Ω andg∈Ywithg(a)=0,are there functionsf1,···,fn∈Ysuch that

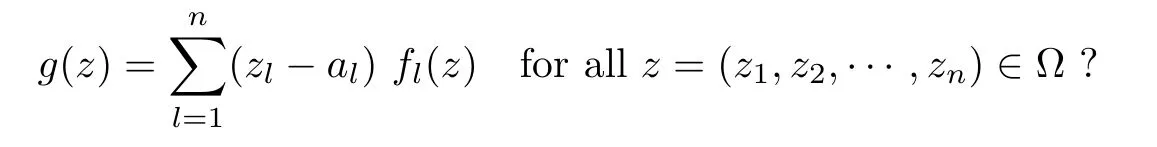
There have been many works addressing Gleason’s problem,for example [12–26].We know that Gleason’s problem is solvable onF(p,q,s) (see [26]).Is this problem also solvable onFp,q,s(B) ? In this paper,we seek to solve this problem.

The following function spaces are also used in this paper:

Definition 1.2For 0＜β≤1,the functionfis in the Lipschitz space Lipβ(B) if

The space Λβ(B)=Lipβ(B) ∩H(B) is called a holomorphic Lipschitz space.By Theorem 7.9 in [27],if 0＜β ＜1,thenf∈Λβ(B) if and only iff∈H(B) and

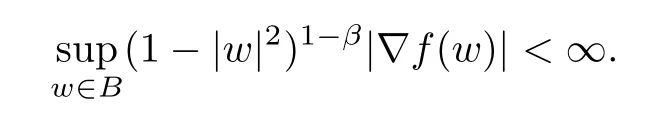
Definition 1.3Forα ＞-1 andp ＞0,the functionf∈H(B) is said to belong to the weighted Bergman space(B) if

where dvα(w)=cα(1 -|w|2)αdv(w),with the constant

2 Some Lemmas

Lemma 2.1(see [14]) Forδ ＞-1,the integrals

have the following properties:

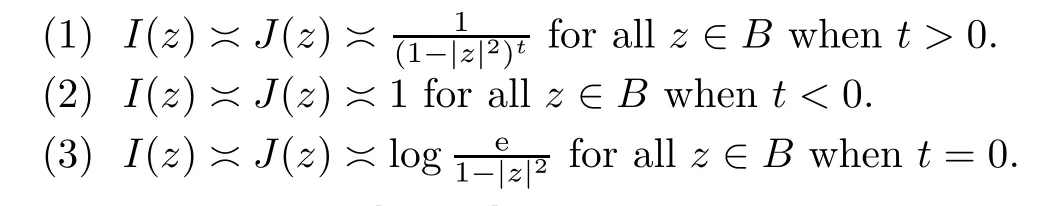
Lemma 2.2(see [28,29]) Letwandabe two points inB.Forl ＞0 andt ＞0,let

Then the following results hold:

Lemma 2.3Fors≥0,p ＞0,q+n≥0,q+s≥0,ifh∈Fp,q,s(B),then

Moreover,the exponent (q+n)/pis the best possible.

ProofFor anya∈B,let=E*(a,1/3) (see [30]) be the Bergman ball.If,then Lemma 2.20 in [27] shows that

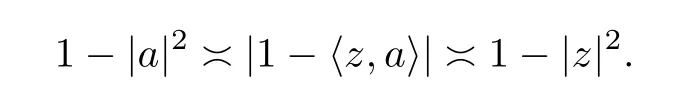
By the proof process of Lemma 2.1 in [30],we may get that

For anyl∈{1,2,···,n},letDlhdenote the partial derivative ofhwith respect to thel-th component.By Lemma 2.24 and Lemma 1.8 in [27],we have that

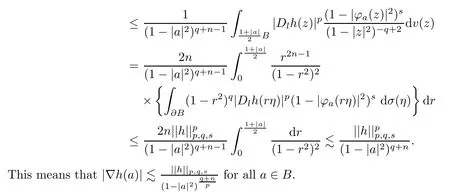
In what follows,we prove that this exponent (q+n)/pis the best possible.

For fixedξ∈∂B,we take

wherew∈B.

Whens=q=0,it follows from Lemma 2.1 that

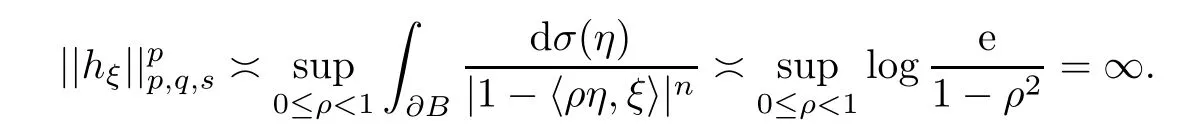
On the other hand,for anyδ ＜n/p,Lemma 2.1 means that

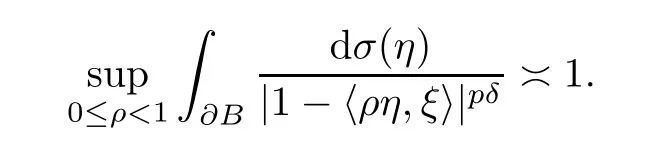
This shows that this exponent (q+n)/pis the best possible whenq=s=0.

In what follows,we consider the other cases.

For the case (i)s≥nandq+n≥0 or (ii)s=0＜q,it is easy to prove that ||hξ||p,q,s≾1,by Lemma 2.1.If 0＜s ＜nandq+s ＞0,thenn(q+n)/(n-s)＞nandn/s ＞1.By Lemma 2.1 and Hlder’s inequality,we have that

Next,we consider the case 0＜s ＜nandq+s=0.

Ifn ＜2s,then Lemma 2.2(3) shows that

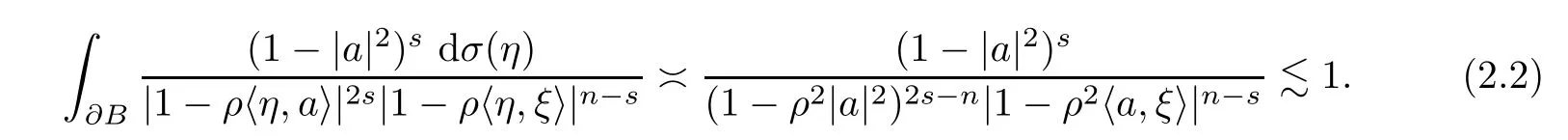
Ifn=2s,then Lemma 2.2(2) and

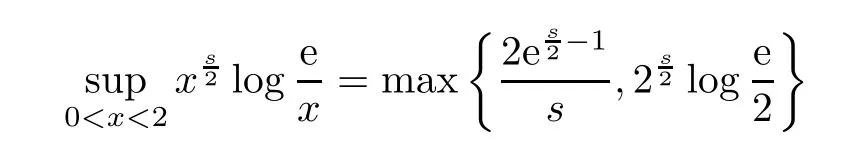
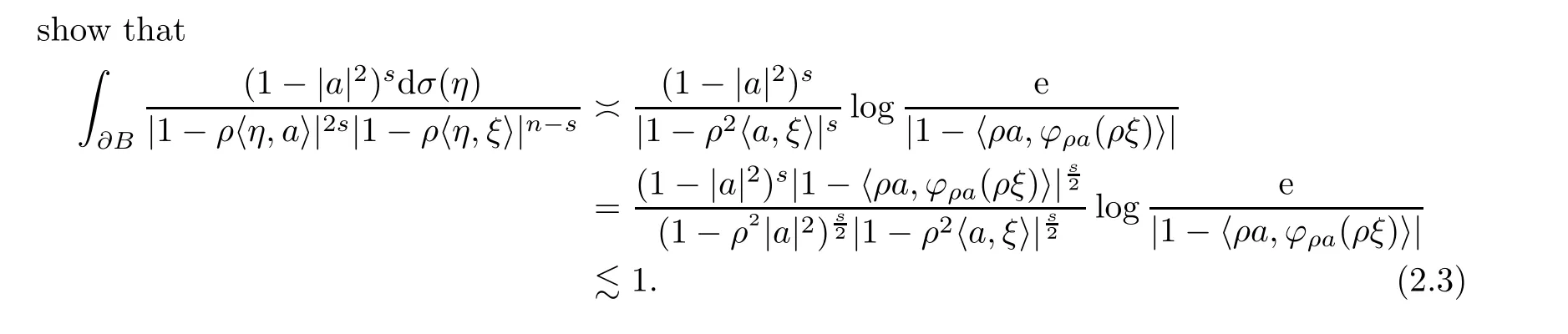
Ifn ＞2s ＞0,then Lemma 2.2(1) means that

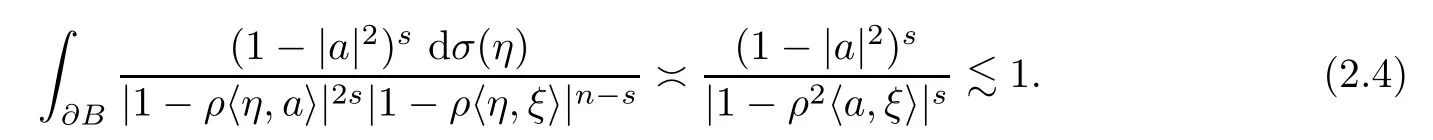
Therefore,(2.1)–(2.4) show that ||hξ||p,q,s≾1.

If there exists someδ ＜(q+n)/psuch that

This contradiction shows that the exponent (n+q)/pis the best possible.

This proof is complete. □

Lemma 2.4(see [29]) Forδ ＞-1 and 0 ≤ρ ＜1,the integral

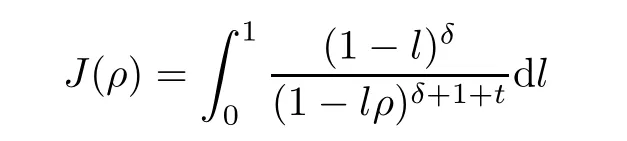
has the following asymptotic properties:

(1)J(ρ) ≍(1 -ρ)-twhent ＞0.

(2)J(ρ) ≍1 whent ＜0.

(3)J(ρ) ≍logwhent=0.

3 Main Results

In order to consider the solvability of Gleason’s problem onFp,q,s(B),we first prove the following result:

Theorem 3.1Lets≥0,p ＞0,q+n≥0,q+s≥0,0＜β ＜1,α ＞β/2+max{1/p-1,0}n-1 andα ＞max{1/p,1} max{q+s,q+n}+max{1/p-1,0}n-1,l∈{1,2,···,n}.Ifφ∈Lipβ(B),then

for allh∈Fp,q,s(B),where

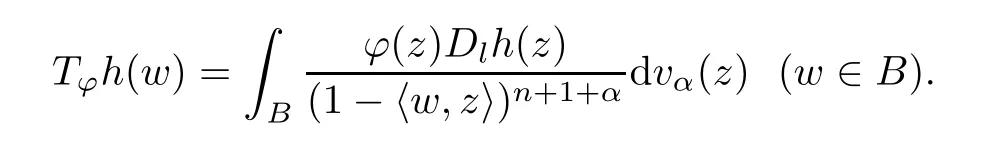
ProofWhenφ∈Lipβ(B),it is clear that

Otherwise,ifz,w∈B,then we have that

We first consider the operator

By (3.2) andφ∈Lipβ(B),we have that

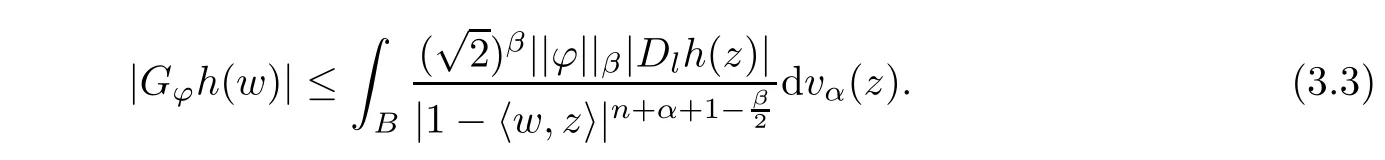
For any 0 ≤ρ ＜1 anda∈B,let

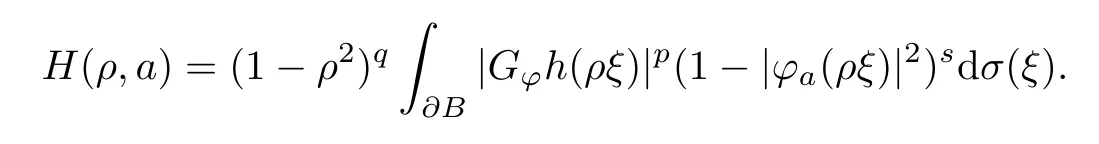
(i) Casep ＞1.

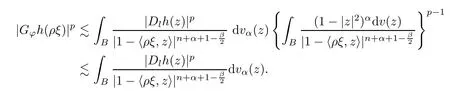
This means that

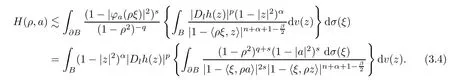
When 2s ＜n,by (3.4) andn+α+1 -β/2＞n,Lemma 2.2(3),Lemma 1.8 in [27],α-q-s ＞-1 and Lemma 2.4,,we may obtain that

When 2s ＞n,by (3.4) andn+α+1 -β/2＞n,Lemma 2.2(4),Lemma 1.8 in [27],α-q-s ＞-1 and Lemmas 2.3–2.4,,s+(q+s)-(2s-n)=q+n≥0,α-q-n ＞-1,Lemma 2.1,s+(q+s)-(2s-n)-(n+α+1-β/2)+(α-q-n)+n+1=β/2＞0,

we can get that

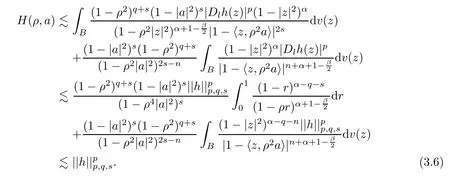
When 2s=n,the conditionsq+s≥0 andα ＞q+n-1 mean that we may chooseδ0=min{(n-β)/4,(α-q-n+1)/2} such thatα-q-n-δ0＞-1,q+2s-δ0≥(α+n+1 -β/2 -2δ0) -(α-q-n-δ0) -n-1=q+2s-β/2 -δ0＞0.By (3.4),Lemma 2.2(5),Lemma 2.3 and Lemma 2.1,we have that

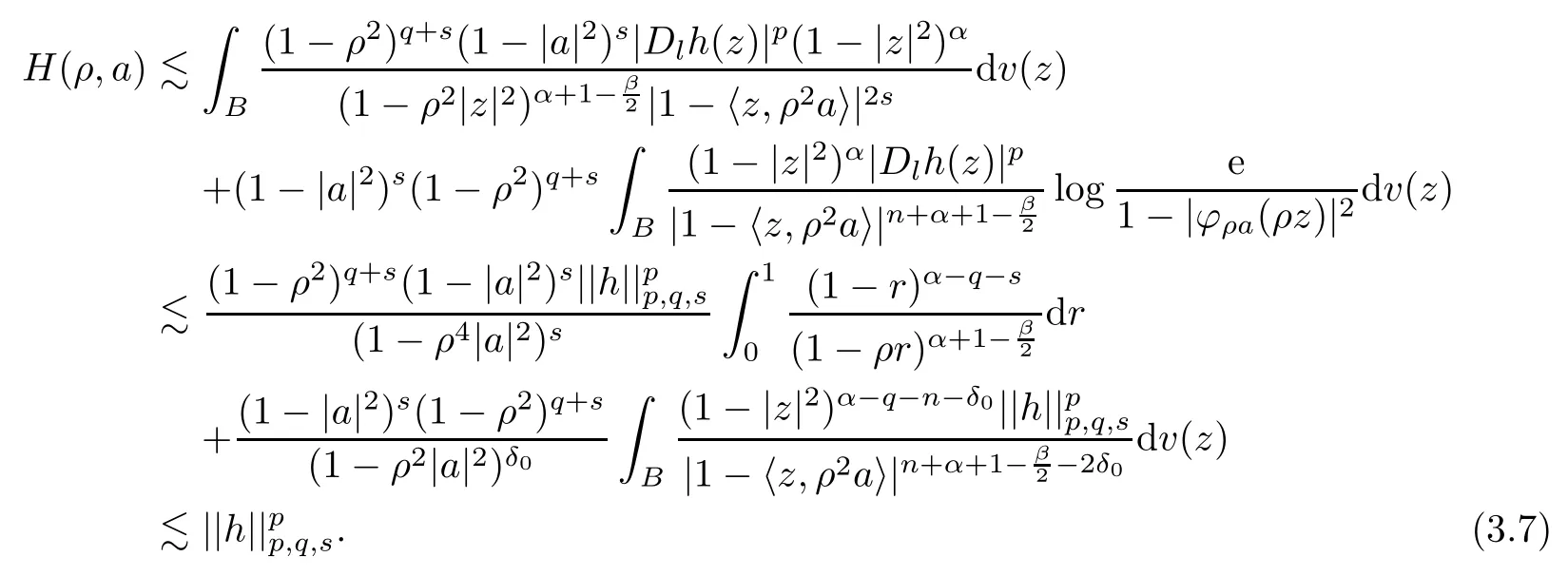
(ii) Case 0＜p≤1.

Forw∈B,we take(z∈B).Applying Lemma 2.15 in [27] toHw,we can obtain that

The above inequality and (3.3) mean that

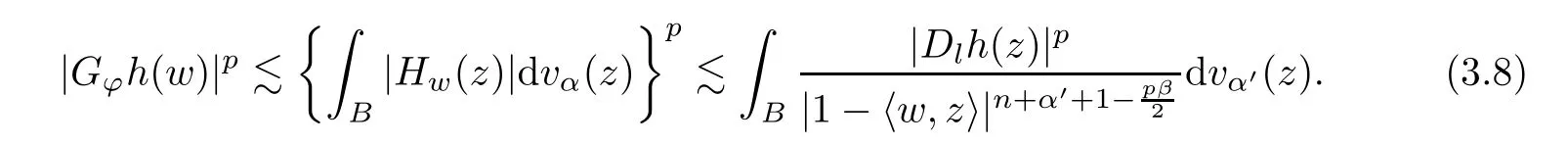
Therefore,by (3.8) and Fubini’s theorem,we may get that

Using (3.9),as long as we usepβ/2 andα′to replaceβ/2 andαin (3.4),respectively,the rest of the proof is similar to the proof of casep ＞1.

The above result and (3.5)–(3.7) mean that we have proved that

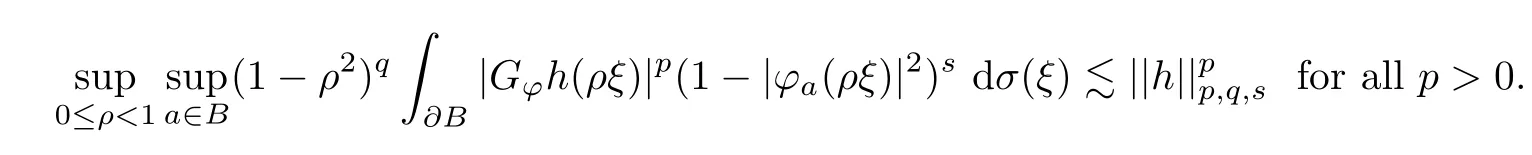
Lemma 2.3 means thatDlh∈(B) whenα ＞(q+n)/p-1 andh∈Fp,q,s(B).It follows from Theorem 2.2 in [27] that

Therefore,Tφh(w)=φ(w)Dlh(w) -Gφh(w).By (a+b)p≍ap+bpfor alla≥0 andb≥0,φ∈Lipβ(B) ⊂C(),we can get that

This means that (3.1) holds.This proof is complete. □

Next,we discuss the solvability of Gleason’s problem onFp,q,s(B).

Theorem 3.2Lets≥0,p ＞0,q+n≥0 andq+s≥0.For any integerγ≥1 anda∈B,there exist bounded linear operatorsWm(|m|=γ) onFp,q,s(B) such that

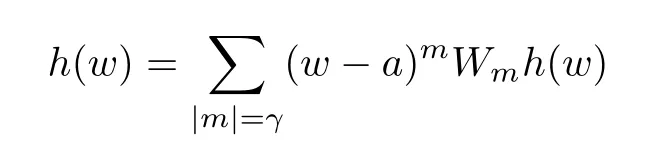
for anyh∈Fp,q,s(B) andw∈BwithDλh(a)=0 (|λ|=0,1,···,γ-1),wheremandλare multi-index.

ProofWe mainly consider the caseγ=1.

For fixeda∈Bandl∈{1,2,···,n},we take that

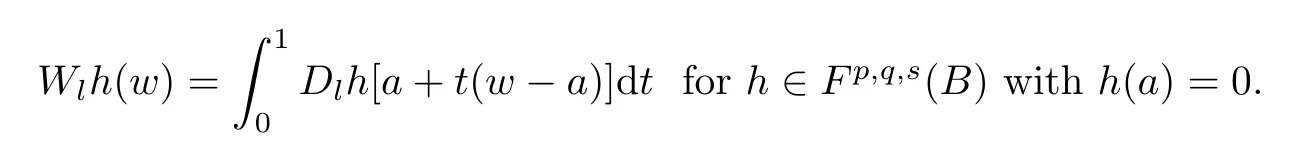
ThenWlis a linear operator and

In what follows,we prove thatWlis bounded onFp,q,s(B) for everyl∈{1,2,···,n}.

We take a positive integerα ＞max{1/p-1,0}n-1/2 andα ＞max{1/p,1} max{q+s,q+n}+max{1/p-1,0}n-1.By (3.10)–(3.11),Fubini’s theorem and a simple calculation,we have that

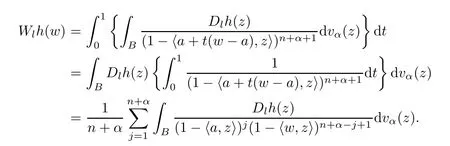
For anyk∈{1,2,···,n},it is clear that

We consider the operator

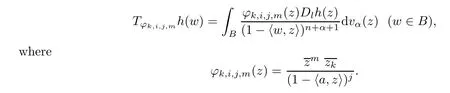
Forγ≥2,the proof is similar to that of Theorem 5 in [25].The main difference is that the calculation is more difficult.We omit the details here.

The proof of Theorem 3.2 is complete. □