THE ASYMPTOTIC BEHAVIOR AND SYMMETRY OF POSITIVE SOLUTIONS TO p-LAPLACIAN EQUATIONS IN A HALF-SPACE*

School of Science,Nantong University,Nantong 226007,China

E-mail: nttccyj@ntu.edu.cn

Lei WEI (魏雷)

School of Mathematics and Statistics,Jiangsu Normal University,Xuzhou 221116,China

E-mail: wlxznu@163.com

Yimin ZHANG (张贻民)†

Center for Mathematical Sciences,Wuhan University of Technology,Wuhan 430070,China

E-mail: zhangym802@126.com

Abstract We study a nonlinear equation in the half-space with a Hardy potential,specifically, where Δp stands for the p-Laplacian operator defined by ,p ＞1,θ ＞-p,and T is a half-space {x1 ＞0}.When λ ＞Θ (where Θ is the Hardy constant),we show that under suitable conditions on f and θ,the equation has a unique positive solution.Moreover,the exact behavior of the unique positive solution as x1 →0+,and the symmetric property of the positive solution are obtained.

Key words p-Lapacian;Hardy potential;symmetry;uniqueness;asymptotic behavior

1 Introduction

In this work,we investigate the existence,uniqueness,asymptotic behavior and symmetry of positive solutions to a class ofp-Lapacian equation,

where Δpstands for thep-Laplacian operator defined by Δpu=div(|∇u|p-2∇u) (p ＞1),andT={x=(x1,x2,· · ·,xN) :x1＞0} (N≥2),θ ＞-p.The first term on the right-hand side of (1.1) contains a singular potentialwhich is a well-known Hardy potential.In the second term,the weight function is,which is degenerate on∂Twhenθ ＞0,and singular on∂Twhenθ ＜0.

For when the potential function has no singularity,problem (1.1) has drawn a lot of attention;for this,we refer readers to [5,6,8–10,18].

Note that if Ω is a bounded smooth domain in RN(N≥2),1＜p ＜∞,the well-known Hardy inequality is (see [12,13])

Here and in what follows,d(x)=d(x,∂Ω).The issue of finding the best constant which is called a Hardy constant is naturally associated with the variational problem of determining

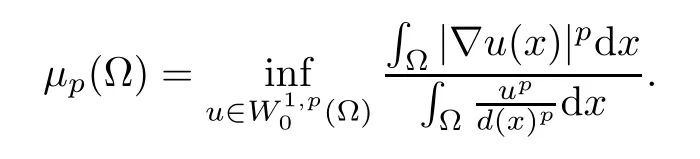
When the dimensionN=1 or when Ω is a convex domain,the Hardy constant is given by (see[1] or [12])

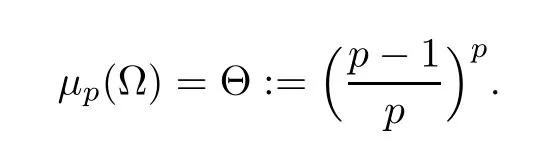
As we know,equation (1.1) serves as ap-Laplacian model for a more general problem in a domain Ω ⊂RN(N≥2),

whereq ＞1,θ ＞-2.For when Ω is a bounded smooth domain,Bandle,Moroz and Reichel in[3] gave some classification of positive solutions to (1.2) for the caseλ≤1/4 (the Hardy constant forp=2),whereas,Du and Wei in [7] considered the caseλ ＞1/4,and obtained the uniqueness and the exact behavior of positive solutions.For when the domain is a half-space,Wei,in [16],studied the case ofλ ＞1/4 and established that (1.2) has a unique positive solution which depends only onx1,and they obtained the exact blow-up rate.Moreover,Bandle,Marcus and Moroz in [2] considered (1.2) withθ=0,λ ＜1/4,and they obtained the existence,uniqueness,nonexistence and the estimate at the boundary of positive solutions.A similar problem with singular potential can be seen in [11,17].

Motivated by the works [7,16],our objective in this paper is to extend the results of [16]to thep-Laplacian equations.We have to overcome some extra difficulties stemming from the nonlinearity of thep-Lalacian operator.In fact,the argument for proving the uniqueness in[16],where the convexity condition offand the linearity of the operator are used,is invalid for thep-Laplacian problem.In addition,the method need to establish the exact blow-up rate in this paper is different from that of [16],and it appears to be new.

We first give the definition of positive solutions of (1.1),which means the following:

Definition 1.1A functionuis said to be a positive solution (subsolution,supersolution)of (1.1) ifu(x) ∈C1(T) withu(x)＞0 inT,and for all functions (non-negative functions)φ(x)in(T),

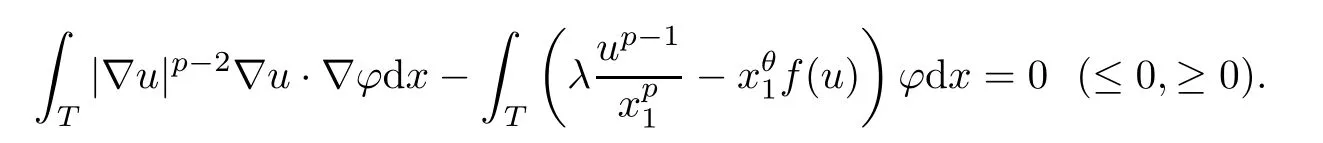
Throughout this paper,we always assume thatand that the following conditions hold:

(f1)f∈C1([0,∞)) andu-(p-1)f(u) is increasing in (0,∞);

(f2),wherer ＞p-1 anda ＞0;

(f3),whereq ＞p-1 andb ＞0.

We always assume thatθ ＞-p,unless otherwise specified.

For convenience,denote that

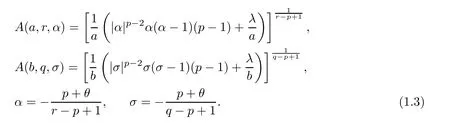
In order to give some information ragarding positive solutions of (1.1),as the arguments in [16] do,we need to establish some key results for the corresponding ordinary differential equation

This is given by the following theorem:

Theorem 1.2Suppose thatθ ＞-p,α,σ,A(a,r,α) andA(b,q,σ) are defined in (1.3).Then the following results hold:

(i) Equation (1.4) has a minimal positive solutionω0and a maximal positive solutionω∞,and any positive solutionωof it satisfies that

(ii) Ifθ≥0,then (1.4) has a unique positive solutionω,and there are positive constantsC1,C2,s*,S*such that

(iii) Ifθ≥0,the unique positive solutionωof (1.4) satisfies that

Corollary 1.3Suppose thatθ≥0,c ＞0 andr ＞p-1＞0.Then

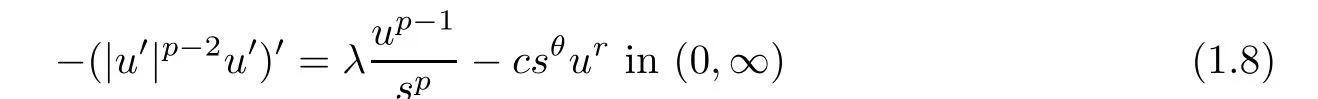
has a unique positive solutionu.Moreover,u(s)=A(c,r,α)sα,whereA(c,r,α) is defined in(1.3).

For a wide class of nonlinear termsf(u),Du and Guo [6] studied the quasilinear equation

withu|∂T=0,whereTis defined as in (1.1).They showed that any positive solution onTmust be a function ofx1only.We can show that this result also holds for problem (1.1).The conclusion can be given by the following theorem:

Theorem 1.4Suppose thatθ≥0.Then,there exists a unique positive solutionW(x)of problem (1.1).Moreover,Wis a function ofx1and satisfies that

whereα,A(a,r,α) andA(b,q,σ) are given in (1.3).

The rest of this paper is organized as follows: in Section 2,we give some preparations,which include two comparison principles and some relations between the Hardy constant and the first eigenvalue.We establish some estimates of positive solutions of (1.4) and prove Theorem 1.2(i) and (ii) in Section 3.Section 4 is devoted to establishing the exact behavior of the unique positive solution to (1.4) and the proof of Theorem 1.2 (iii).In Section 5,we prove Theorem 1.4;that is,we give the existence,uniqueness,asymptotic behavior and symmetry of positive solutions to (1.1).

2 Preparations

2.1 Comparison Principle

First,we cite a comparison result for a class of quasilinear equations ([5,Proposition 2.2]).It is noteworthy that the comparison principle is never obvious for quasilinear operators.

Lemma 2.1Suppose thatDis a bounded domain in RN,and thatα(x) andβ(x)are continuous functions inDwith ‖α‖L∞(D)＜∞andβ(x) ≥0,β(x)0 forx∈D.Letu1,u2∈C1(D) be positive inDand satisfy,in the sense of distribution,that

For the unbounded region,if the subsolution has a suitable estimate,then we also have the following comparison principle:

Lemma 2.2Forτ ＞0,let (f1) hold,and letu1andu2be,respectively,a positive supersolution and a subsolution of

If there are positive constantsCandSsuch that

thenu1(s) ≥u2(s) in (τ,∞).

ProofLetφ1,φ2be nonnegative functions in(τ,∞).Sinceu1is a supersolution andu2is a subsolution of (2.1),a simple calculation gives that

For any∈＞0,denote that

The condition (2.2) implies thatv1,v2are zero nears=τ,andv1,v2are also zero whensis sufficiently large.Hence,v1andv2belong tofor some Ωτ⋐(τ,∞),and are zero outside Ωτ.By an approximate method,v1andv2can be test functions.

Denote that

For convenience,this expression can be simplified by using

A calculation as the proof of Proposition 2.2 in [5] shows that there isc:=c(p)＞0 such that

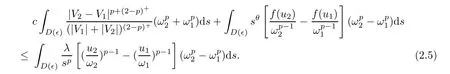
Denote the right hand side of the inequality (2.5) byJ(∈).We claim thatJ(∈) →0 as∈→0.For anyδ ＞0,we denote that

By the condition (2.3),whenδis sufficiently small,there isC ＞0 independent ofδsuch that

From the definition ofD(∈),it is clear that

Due toq ＞p-1＞0,we have that.For anyη ＞0,we may first fix a sufficiently smallδ ＞0 such that,for sufficiently small∈＞0,

Clearly,M(∈) →0 as∈→0.Taking this together with (2.6),we obtainJ(∈) →0 as∈→0.

As the final proof of Proposition 2.2 in [5],J(∈) →0 implies thatD(0)=Ø.Furthermore,it holds thatu1(s) ≥u2(s) whens≥τ.□

2.2 Relation Between the Hardy Constant and the First Eigenvalue

Now we give some relations between the Hardy constant and the first eigenvalue.Assume thatλ1[(δ,L),1/sp] is the first eigenvalue of

Assume that Ω ⊂RN(N≥2) is bounded and thatλ1[Ω,α(x)] is the first eigenvalue of

Hereα(x) is a positive continuous function over Ω.Set

ProofThe conclusions (i) and (iii) can be obtained by the method used in [16,Lemma 2.2].Here,we only give the proof of the conclusion (ii).For a givenδ ＞0 and small∈＞0,suppose thatφ1(s)＞0 is the first eigenfunction with respect toλ1[(∈,1),1/sp];that is,thatφ1(s) satisfies

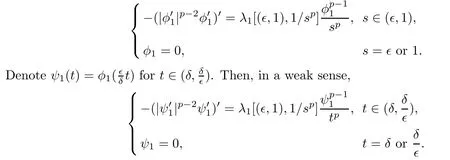
3 Some Estimates and the Uniqueness of Positive Solutions to (1.4)

3.1 The Minimal Positive Solution and the Maximal Positive Solution to (1.4)

In this subsection,the existence of the minimal positive solution and the maximal positive solution of (1.4) will be proved.

Proposition 3.1Equation (1.4) has a minimal positive solutionω0and a maximal positive solutionω∞.

ProofAssuming thatn,mare positive integers,consider problems

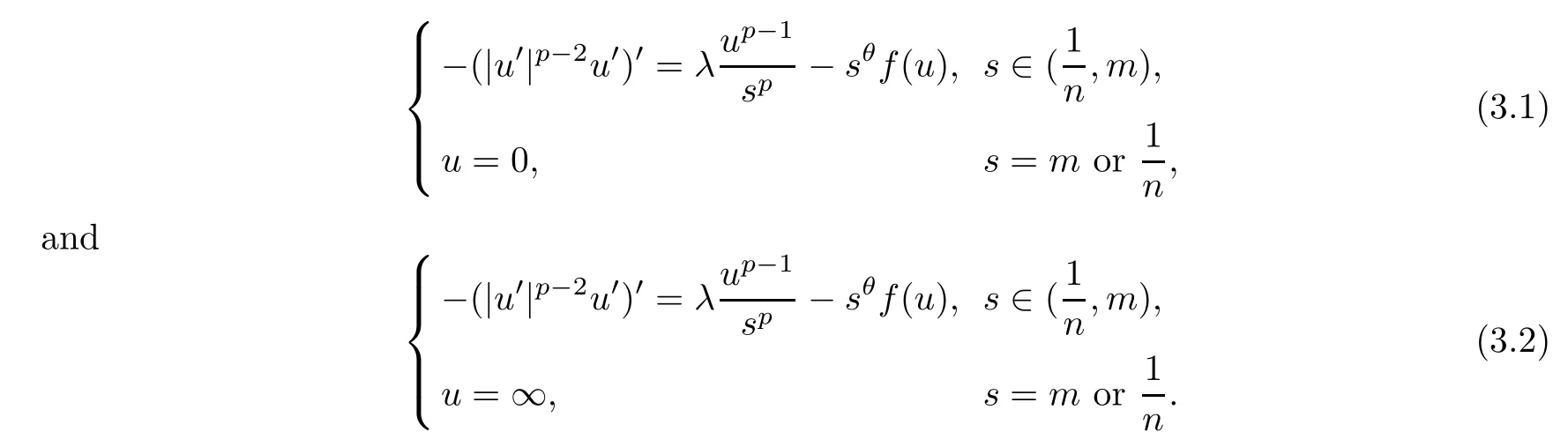
Sinceλ ＞Θ,in view of Lemma 2.3,there existn0andm0such that,for anyn≥n0andm≥m0,one hasλ ＞λ1[(1/n,m),1/sp].From [15,Theorem 9.6.2],there is a unique positive solutionωn,mof (3.1) whenn≥n0andm≥m0.Using Lemma 2.1,we can deduce thatωn,mis nondecreasing inmandn,respectively.Sincefsatisfies (f1) and (f2),we know that (3.2)has a unique solutionun,m(see [4,5]).Using Lemma 2.1,we know thatun,mis non-increasing with respect tomandn,respectively.For 0＜≤nand 0＜≤m,Lemma 2.1 also implies that

Letφbe an arbitrary positive solution to (1.4).For anys∈(1/n,m),Lemma 2.1 indicates thatun,m(s) ≥φ(s).Then,φ(s) ≤ω∞(s) in (0,∞),by lettingn→∞andm→∞.Hence,ω∞must be the maximal positive solution of (1.4).By a method similar to that used above,we can prove thatω0is the minimal positive solution of (1.4). □

Next,we will consider the behaviors ofω0andω∞near the origin and infinity.

Proposition 3.2Assume thatω0is the minimal positive solution of (1.4).Then,(s) ≤0.Moreover,ω0blows up at the origin.

ProofFrom Proposition 3.1,to show(s) ≤0,it suffices to prove that

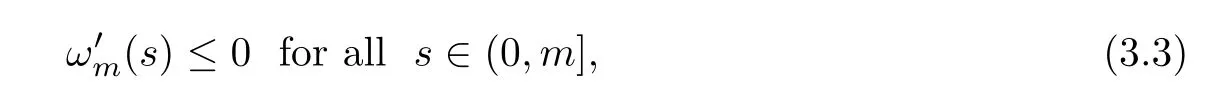
whereωmsatisfies that

The strong maximal principle [14] implies that(m)＜0.In view of the continuity of(s)with respect tos,(s)＜0 holds whens ＜mis close tom.Set

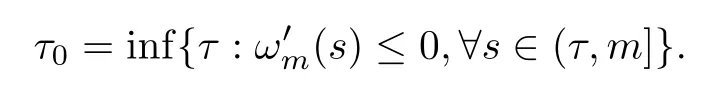
We claim thatτ0=0.By contradiction,we assume thatτ0∈(0,m).

Case 1If there isτ1∈(0,τ0) such that,(τ1)＜0,then there existsτ1＜s1＜s2≤τ0such that

hold.In fact,if (3.5) or (3.6) is not true,then there exists a positive constantδsuch thats1+2δ ＜s2,and

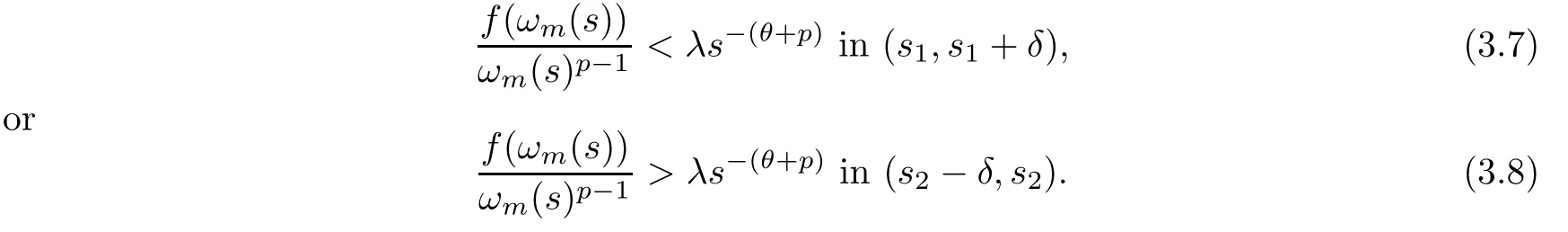
If (3.7) holds,by integrating the equation in (3.4) froms1tos1+δ,we have that

Thus,we can see a contradiction.Similarly,if (3.8) holds,by integrating the equation in (3.4)froms2-δtos2,we have that

which is a contradiction.

On the other hand,when (3.5) and (3.6) hold,bys1＜s2and -(p+θ)＜0,we have that

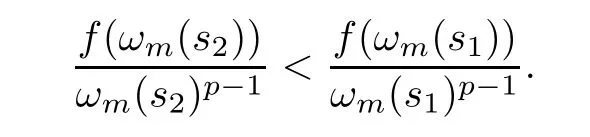
From (f1),the above formulation contradicts with the fact thatωm(s1)＜ωm(s2).Therefore,Case 1 does not apply.

Case 2If,for almost alls∈(0,τ0),(s) ≥0 holds,then,

Usingθ ＞-p,(f1) and (f3),we can deduce that

Hence,fromλ ＞Θ,there isς∈(0,m) such that

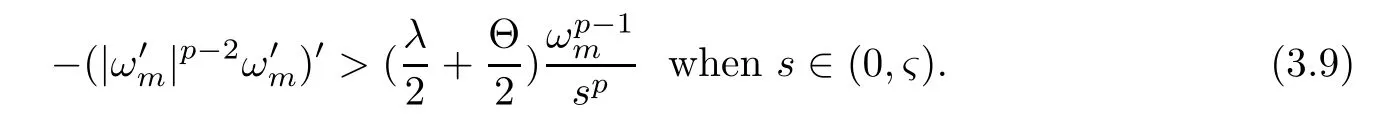
Clearly,for any∈＜ς,ωmis a strictly positive supersolution of

Then,for all∈∈(0,ς),which contradicts with the fact thatλ1[(∈,ς),1/sp] →Θ as∈→0+.

Finally,we will prove thatω0blows up ats=0.If this were not the case,then,for alls ＞0,it would follow from(s) ≤0 that∈(0,∞).As such,a contradiction is obtained. □

Remark 3.3Sinceω0is the minimal positive solution of (1.4) andω0(s) →∞ass→0+,any positive solutionuof (1.4) blows up at the origin.

Proposition 3.4Assume thatω∞is the maximal positive solution of (1.4).We have

ProofBy arguing indirectly,we suppose thatω∞(s) ∈(0,∞].

Since(s) always exists for alls∈(0,∞),by virtue of the convexity and the concavity,there ares2＞s1＞0 such thatω∞(s1)＜ω∞(s2),(s) is nondecreasing nears1,and(s) is nonincreasing nears2.Thus we have that

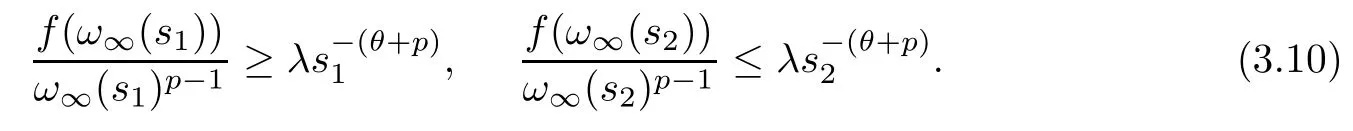
In fact,by the argument for (3.5) and (3.6),we obtain (3.10),which implies that

Using (f1),the above formulation contradicts with the fact thatω∞(s1)＜ω∞(s2).

Fors∈(-1,1),lett1＞2s0and define.A calculation gives that

Assuming thatφ∞(s) is the unique positive solution of the problem (see [5]),

Forθ≥0 ands∈(-1,1),using the comparison principle,we can deduce thatφ(s) ≤φ∞(s).Takings=0,we get that

Then,forθ≥0,fromα ＜0 and the arbitrariness oft1,one has that,which is a contradiction.The caseθ ＜0 can been obtained by a similar proof.Then,holds. □

Proof of Theorem 1.2 (i)By Propositions 3.1–3.4,we can directly see that Theorem 1.2 (i) holds. □

3.2 Some Estimates and the Uniqueness of Positive Solutions of (1.4)

In this subsection,some estimates of positive solutions of (1.4) will be given.First,we establish the existence and uniqueness results of the following auxiliary problem:

Proposition 3.5Suppose thatL ＞0 andθ≥0.Then,the problem

has a unique positive solutionu=ω(s),where,s∈(0,L),andv[γ,L](s)is the unique positive solution of the problem

Moreover,there ares*andC ＞0 such that

ProofFor a givenλ ＞Θ,by Lemma 2.3,there existsγ0∈(0,L/2) such that,for anyγ∈(0,γ0],we have thatλ ＞λ1[1/sp,(γ,L)].Thus,for suchγ,problem (3.12) has a unique positive solutionv[γ,L].We denote bythe minimal positive solution of the problem

are the minimal and maximal positive solutions,respectively,of (3.11) in (0,L].As in the proof of Proposition 3.2,we can obtain thatω(s) →∞ass→0+.

In order to show the uniqueness of positive solutions of (3.11),we only need to show that,for any positive solutionωLof (3.11),ωL(s) ≥Φ(s) holds in (0,L].SinceωLis positive in(0,L),we have thatωL(L-γ)＞ωL(L).Define an auxiliary function

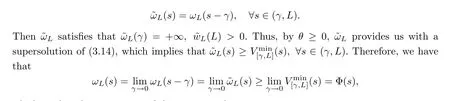
which implies the uniqueness of the positive solutions.

For any∈∈(0,γ0) ands∈(∈,L∈/γ0),set

Then,the function Ψ satisfies the problem

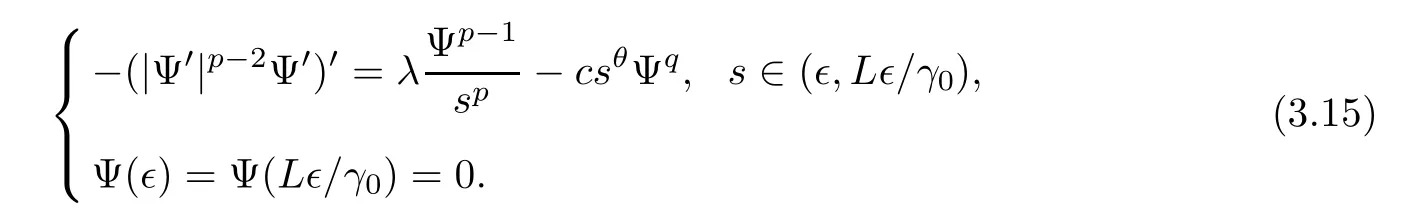
Moreover,we can deduce thatω(s) is a positive supersolution of problem (3.15),and it follows that for anys∈(∈,L∈/γ0),Ψ(s) ≤ω(s).Fromγ0＜L/2,we can know that 3∈/2 ∈(∈,L∈/γ0).Then,for∈∈(0,γ0),we have that

Proposition 3.6Letω0be the minimal positive solution of (1.4).Then,there areC ＞0,s*andS*＞0 such that

whereαandσare defined as in (1.3).

ProofUsing (i) of Theorem 1.2 and (f2),there areℓ ＞0 andc*＞0 such that

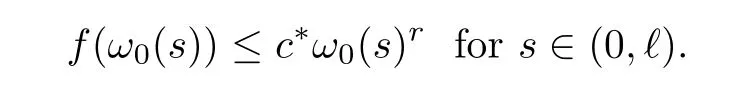
Hence,we have that

Sinceω0is a supersolution of (3.12) withLreplaced byl,from the proof of Proposition 3.5 and(3.13),it follows that (3.16) holds.

Using Proposition 3.4 and (f3),there areL ＞0 andc2＞0 such thatf(ω0(s)) ≤in (L,∞).This indicates that

From (i) of Lemma 2.3,for a givenγ ＞0,there ist0∈(0,γ/2) such thatλ ＞λ1[(t,γ),1/sp] for anyt∈(0,t0].Using standard arguments,there is a unique positive solution for the problem

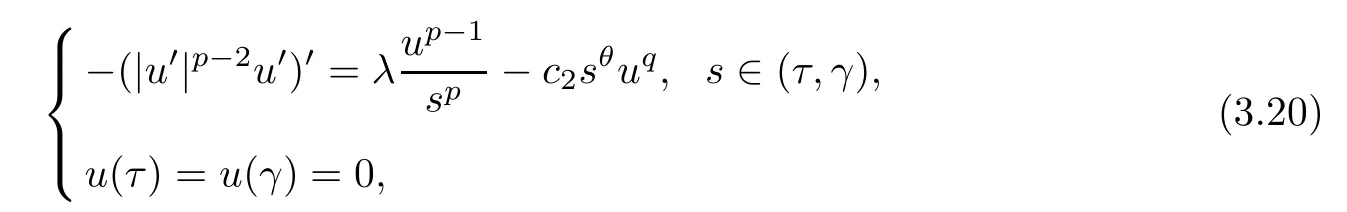
denoted byUt,γ.Set.Forr ＞r*andL≤s≤r,let

By calculating,Ψris a solution of the problem

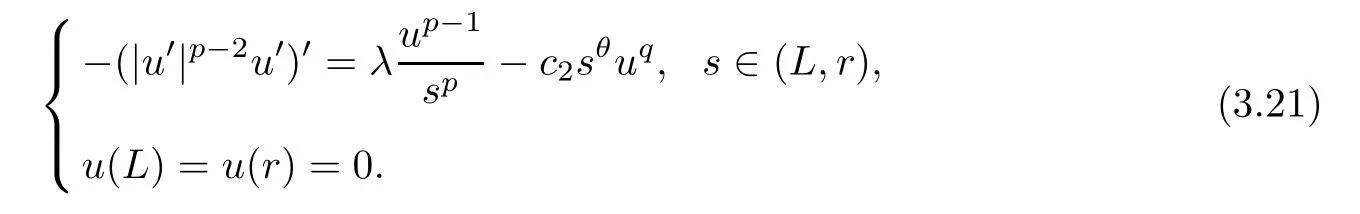
Then,(3.19) indicates thatω0is a supersolution of problem (3.21).It follows from the comparison principle that,for alls∈(L,r),

Then,for arbitraryr ＞r*=max{2L,r*} ands=r/2,it follows from (3.22) that

Fors=r/2 andis nondecreasing with respect tor,we can obtain that

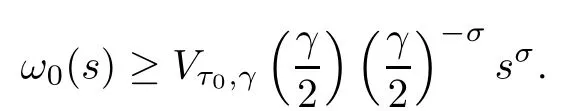
In view of the arbitrariness ofrand takingS*=r*,(3.17) holds. □

Proposition 3.7 There existC2＞0,s*andS*＞0 such that

whereαandσare defined as in (1.3).

Proof Using (i) of Theorem 1.2,(f2) and (f3),there areℓ ＞0,C ＞0 andL ＞0 such thatf(ω∞(s)) ≥Cω∞(s)rass∈(0,ℓ) andf(ω∞(s)) ≥Cω∞(s)qass∈(L,∞).Then,fors∈(0,ℓ),we have that

For anys0∈(0,ℓ/2),setW(s0)={s∈(0,∞): |s-s0|＜s0/2}.It is easy to know thatW(s0) ⊂(0,ℓ).Fors∈(-1,1),set

Ifθ≥0,it follows from (3.25) that

By [5],we know that there exists a unique positive solutionQ∞,rto the following boundary blow-up problem:

Then,the comparison principle shows that,for alls∈(-1,1),it holds thatQ(s) ≤Q∞,r(s).Ifs=0,we have that

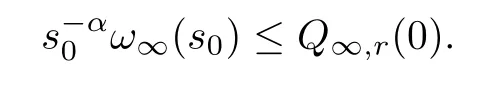
From the arbitrariness ofs0and lettings*=ℓ/2,we can get (3.23).If -p ＜θ ＜0,a similar proof indicates that (3.23) holds.

Letϱ ＞2L,and fors∈(-1,1),.Ifθ≥0,we can deduce that,fors∈(-1,1),

Using the comparison principle,it follows froms=0 thatQ∞,q(0) ≥r-σω∞(ϱ).TakeS*=2L.Then (3.24) holds,in view of the arbitrariness ofϱ.If -p ＜θ ＜0,a similar proof indicates that (3.24) holds. □

Proof of Theorem 1.2 (ii)For any positive solution of (1.4),it follows from Propositions 3.6–3.7 that the inequalities (1.5) and (1.6) hold.

Now we prove the uniqueness of the positive solutions of (1.4).It suffices to show that

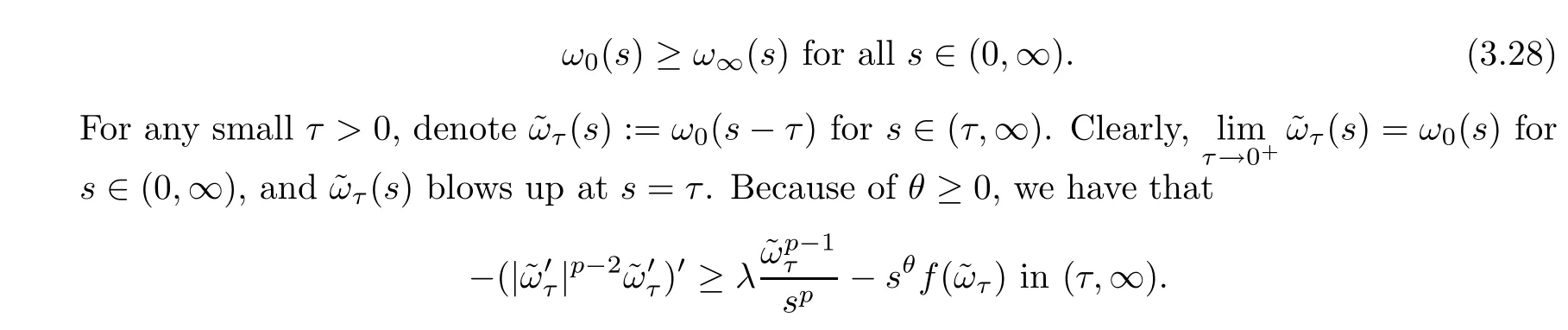
From inequality (3.24) in Proposition 3.7 and Lemma 2.2,it follows that

Furthermore,lettingτ→0+,we obtain (3.28). □

Note that Corollary 1.3 can be derived by Theorem 1.2 (ii).

4 Exact Behaviors of the Unique Positive Solution to (1.4)

Proposition 4.1Suppose thatλ ＞Θ,r ＞p-1＞0,θ≥0,candLare positive constants.Letu0be the unique positive solution of (3.11) and letu∞be the maximal positive solution of

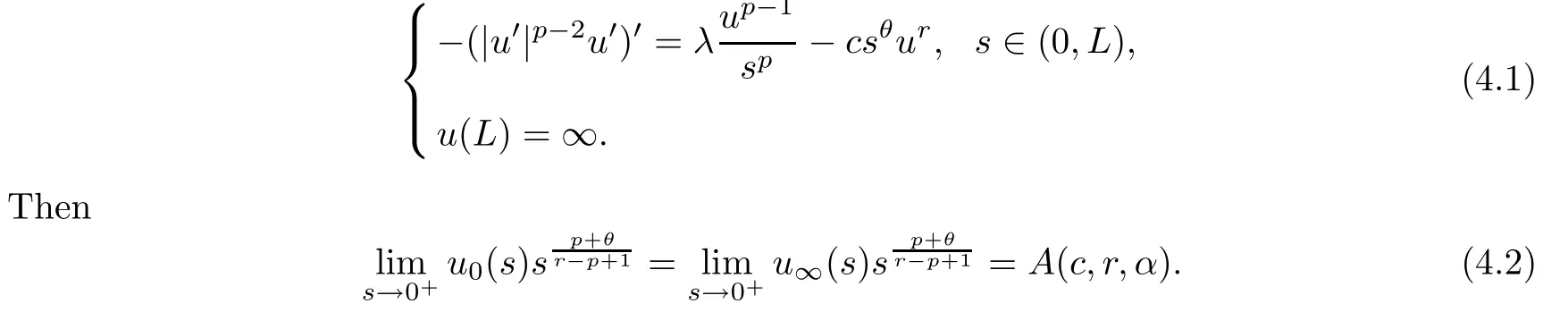
ProofWe first show that (4.1) has a maximal positive solution.By the standard arguments,letunbe the unique positive solution of (see [5])

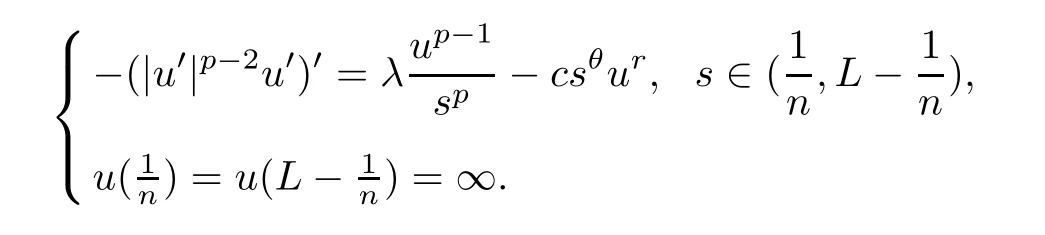
The comparison principle implies thatunis nonincreasing inn.As the proof of Proposition 3.1,we can show thatis the maximal positive solution of (4.1).

Then a simple calculation shows that

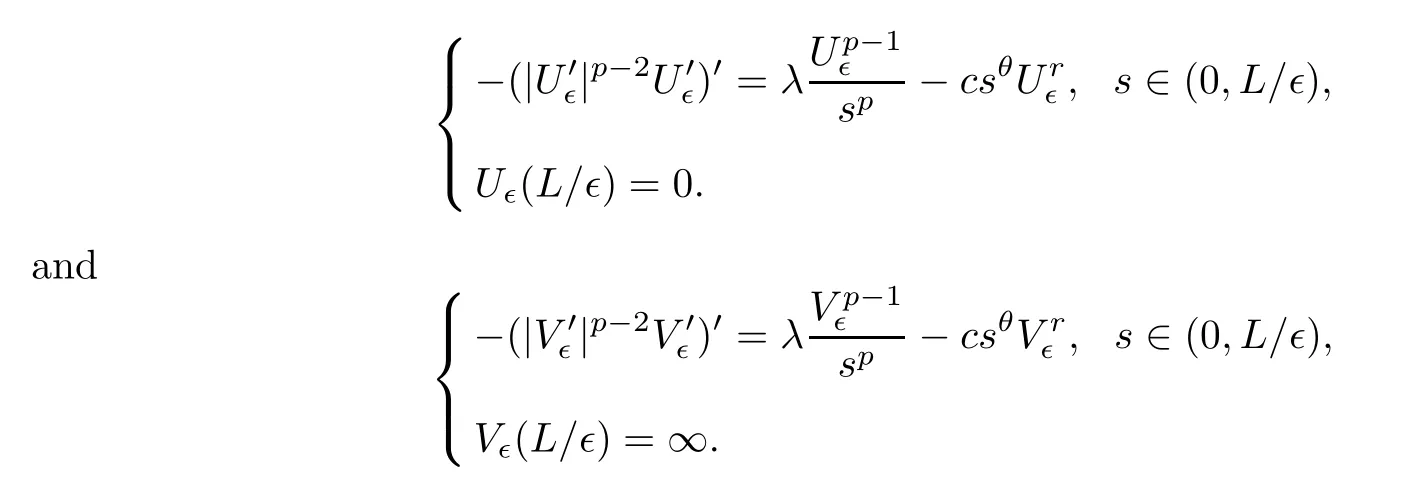
It is not difficult to prove that {U∈} is nonincreasing in∈and that {V∈} is nondecreasing in∈.Moreover,we have that

The regularity theory implies that bothUandVare positive solutions of (1.8).In view of Corollary 1.3,for any 0＜δ ＜K,it follows that

Furthermore,we have that

which implies (4.2). □

Remark 4.2For anyL ＞0,let0be the minimal positive solution of

We first show the existence of the minimal positive solution of (4.4) and the maximal positive solution of (4.5).By Lemma 2.3 (ii),we can take a largeL0＞Lsuch thatλ ＞λ1[(L,l),1/sp]holds for anyl ＞L0.From the standard arguments of logistic equations,it follows that,for anyl ＞L0,

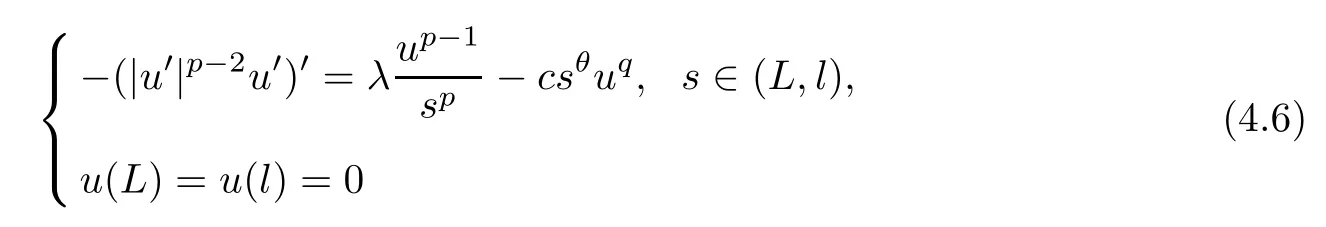
has a unique positive solutionl.By the arguments of the boundary blow-up problems (see[5]),for anyn ＞L+1,the problem

has a unique positive solutionn.As the proof of Proposition 3.1,we obtain thatis the minimal positive solution of (4.4),and thatis the maximal positive solution of (4.5).

Then we have that

As the proof of Proposition 4.1,similarly,we can obtain that

Furthermore,we have that

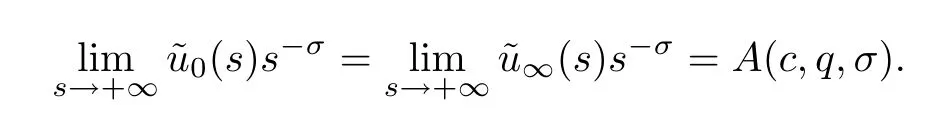
Proof of Theorem 1.2 (iii)Since the unique positive solutionwof (1.4) blows up at the origin,for any∈＞0,by (f2) there is a positive constantLsuch that

Using the comparison principle,it holds that

whereu0(s;∈) is the minimal positive solution of (3.11) withc=a-∈,andv∞(s;∈) is the maximal positive solution of (4.1) withc=a+∈.By Proposition 4.1,we have that

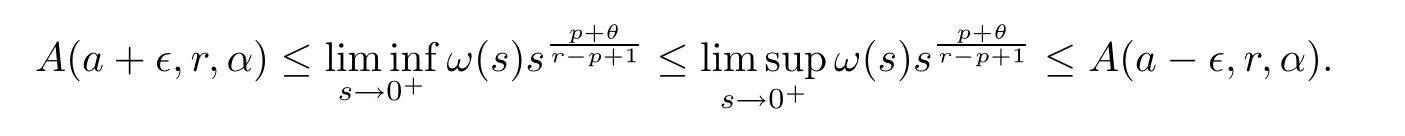
In view of the arbitrariness of∈,we can derive the first equality in (1.7).

Similarly,the second equality in (1.7) can be obtained by using Remark 4.2. □

5 The Proof of Theorem 1.4

Proof of Theorem 1.4The process of this proof is similar to that of [16,Theorem 1.2].□