Ratchet transport of self-propelled chimeras in an asymmetric periodic structure

Wei-Jing Zhu(朱薇静) and Bao-Quan Ai(艾保全)

1School of Photoelectric Engineering,Guangdong Polytechnic Normal University,Guangzhou 510665,China

2Guangdong Provincial Key Laboratory of Quantum Engineering and Quantum Materials,School of Physics and Telecommunication Engineering,South China Normal University,Guangzhou 510006,China

Keywords: Brownian motion,self-propelled particles,stochastic processes

1. Introduction

Self-propelled particles can take energy from the environment and propel themselves into an out-of-equilibrium state.[1,2]Due to the sustained energy uptake and dissipation at the scale of the active unit,these systems exhibit several exotic phenomena that are inaccessible in systems at thermal equilibrium, for instance, swarming, flocking, and the emergence of other collective properties.The phenomenon of collective motion can be observed on vastly different length scales,including in schools of fish,[3]insect groups,[4,5]collections of gliding bacteria,[6-8]driven biopolymers,[9,10]and cellular flows in extended tissues.[11,12]

The external unbiased force can cause the directed motion of the diffusing particles in the ratchet system,which is called rectification. Generally speaking,the ratchet model with rectification can be divided into the following three types:[13](i)Rocking ratchet:[14-16]the transient time asymmetry of the system is caused by the unbiased external force. (ii) Flashing ratchet:[17,18]the asymmetric potential field of the particle randomly transitions between two or more states or adopts the time modulation of the potential to form a directed motion. (iii) Correlation ratchet:[19,20]this model mainly considers the influence of color noise on rectification. In all of the above models, the unbiased driving force can break the thermodynamic equilibrium and induce the rectification of particles. Other types of ratchet models can be summarized as the above three types of extensions or their combinations. For example, a model based on a dual-noise,non-uniform temperature field and an asymmetric spatial environment can be attributed to a rocking ratchet. When the model is proposed in different states, or particles transition between multiple states, the system can be attributed to the flashing ratchet model. Researchers have committed to studying the rectification motion in asymmetric structures from various aspects,such as(i)particle classification: active particles,[21,22]polar particles,[23,24]chiral particles,[25]runtumble particles,[26]and others. (ii)The physical properties of particles: size,shape,and mass.[27,28](iii)Asymmetric structural properties:fixed structures[29]or structures with constant velocity.[30]Most studies on the transport of self-propelled particles have referred to the consideration of the overdamped regime. However,the overdamped approximation is not justified in many situations. The inertial effect of particles exhibits remarkable behaviors,including current reversals and chaotic transport.[31-33]In addition, different noise types[34-36]also have a great influence on the motion of underdamped particles.

Nikita and colleagues studied the stochastic dynamics of self-propelled particles with polar interaction subject to phase lag and revealed the existence of a traveling band, clouds,and vortical structures.[37]However, the influence of rectification has not been considered yet. In this paper, we extend this work[37]by studying the ratchet transport of underdamped particles with polar interaction subject to phase lag. We focus on finding how the inertia effect influences the rectification of particles and investigating the underlying mechanisms of polar interaction and phase lag.

2. Model and methods

We modelNparticles moving in a two-dimensional(2D)space with periodic boundary conditions along thexdirection and hard wall boundary conditions along theydirection (see Fig.1(a)). The shape of the spatially periodic channel is modeled by the half widthh(x),

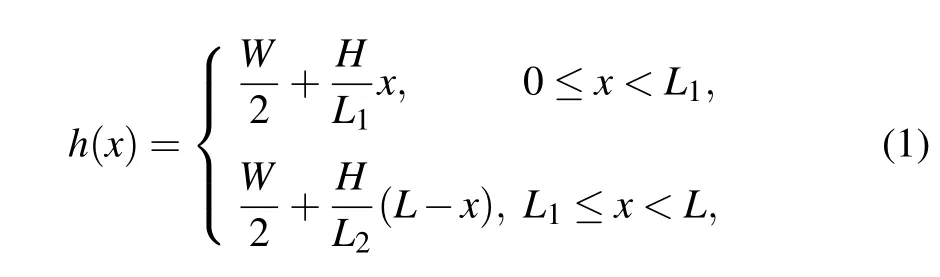
whereLcorresponds to the periodic of the channel,and parametersWand 2H+Wcontrol the minimal and maximal channel width, respectively. The asymmetric parameter is denoted asΔ=(L1-L2)/L. The reflecting channel boundaries are defined by Eq. (1), which ensures the confinement of particles inside the channel.[22]The coordinates of particlesi=1,...,Ncan be described byri ≡(xi,yi) and they are oriented at the angleθiof the polar axisni ≡(cosθi,sinθi). We consider the short range interaction force,Fi=Fxi ex+Fy i ey=∑Fij,acting on particle-particle interactions. Particleievolves according to the following Langevin equation:

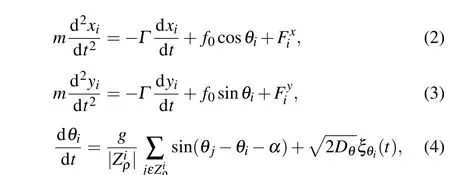
wheremis the mass of the particles,Γis the Stokes friction coefficient,f0is the self-propelled force andDθis the rotational diffusion coefficient.ξθi(t) denotes zero mean white noise with the relation〈ξθi(t)ξθj(t＇)〉=δθiθ jδ(t-t＇).

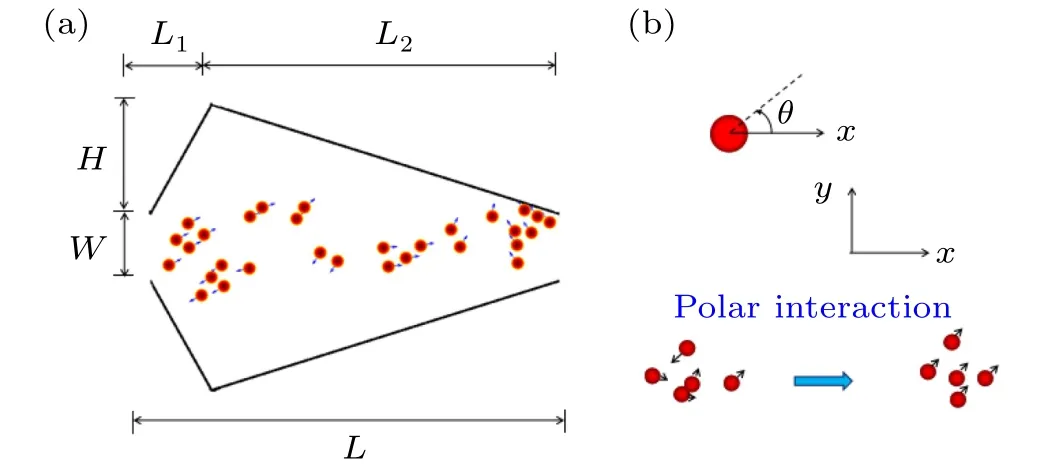
Fig. 1. (a) Schematic illustration of the ratchet device: self-propelled particles move in a two-dimensional periodic channel with periodicity L. The reflecting channel boundaries are defined by Eq.(1),which ensures the confinement of particles inside the channel. (b)Schematic diagram of the polar interaction case. Polar interaction leads to the parallel alignment of the velocity of moving objects.

3. Results and discussion

In the simulation results, the initial position of the particles is randomly distributed in the sample;meanwhile,orientations are also random over the interval[0,2π].We have chosen less than 10-3integration step time and over 107simulation time to reach a steady state. Unless otherwise illustrated, the set parameters areH=4.0,L=15.0,Δ=-0.7,r=0.5,andφa=0.2.

Actually, there are two critical elements of the ratchet setup in nonlinear systems.[41]One is the asymmetry (temporal and/or spatial) that can violate the left-right symmetry of the response because transport in a fully symmetrical system is unbiased. The other is the fluctuating input zeromean force:it should break the thermodynamical equilibrium,which prevents the appearance of any directed transport due to the second law of thermodynamics. For our system, the asymmetry comes from the left-right asymmetry of the channel and the fluctuating input zero-mean force comes from the self-propulsion of active particles.

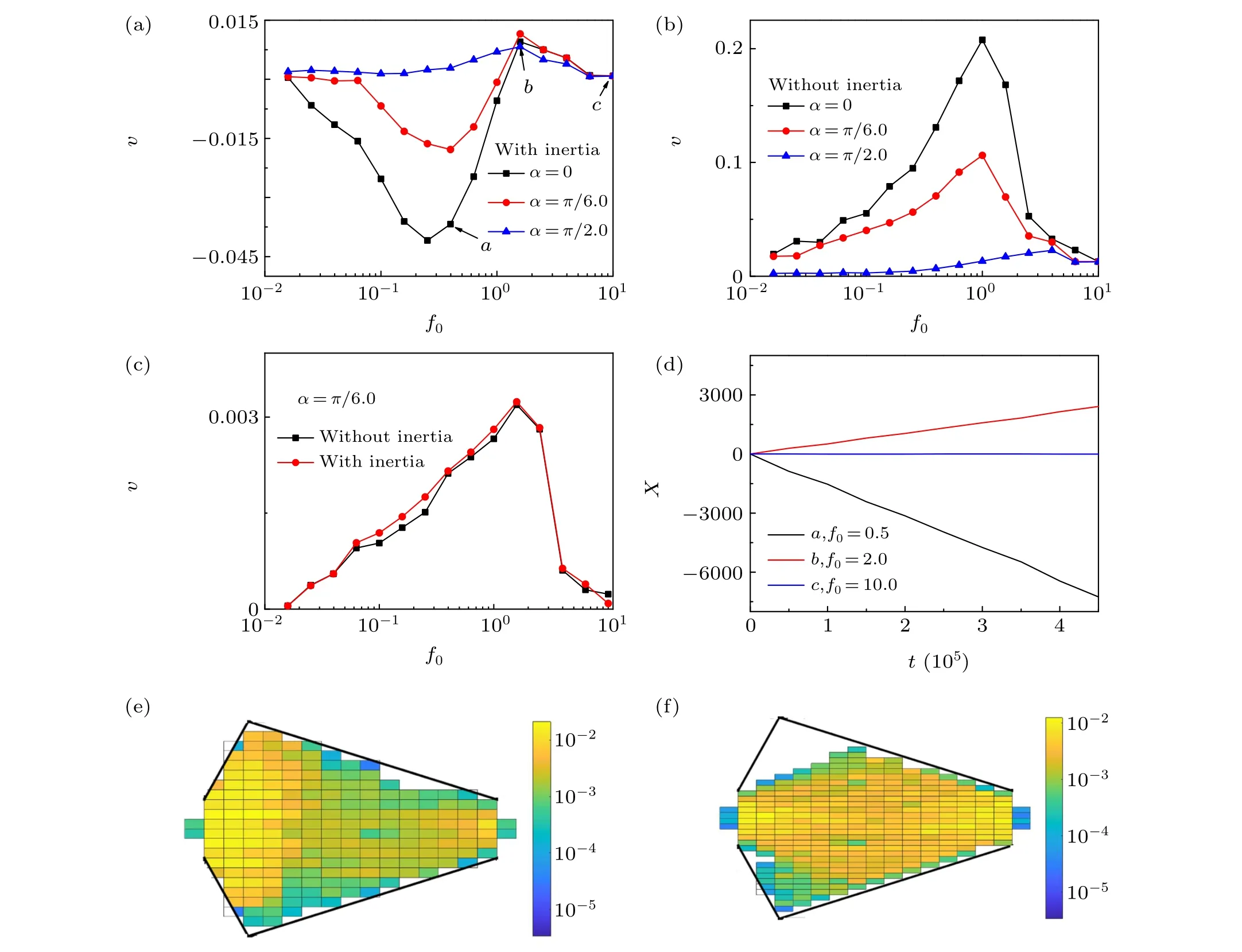
Fig.2. Average velocity v versus the self-propelled force f0 for various values α at Γ =3.0. (a)Underdamped case(with the inertial term). (b)Overdamped case(without the inertial term). (c)Average velocity v versus the self-propelled force f0 at Γ =30.0 and α =π/6.0 when the inertial term is included and neglected. (d) Description of the average position x versus time starting from the random initial condition for various values f0, corresponding to a, b, c in Fig. 2(a). (e) 2D histogram of particle probability density distribution corresponding to a in Fig. 2(a). (f) 2D histogram of particle probability density distribution corresponding to b in Fig.2(a). The other parameters are Dθ =0.01,ρ =1.5,W =3.0,and g=0.1.

For the overdamped case(without inertial term)shown in Fig. 2(b), the particle always moves along the easy direction of the substrate asymmetry (positivev) and no current reversals occur. The ratchet phenomenon can be explained as follows. Note thatΔcontrols the direction of the average velocity.WhenΔ=-0.7,the left side of the structure is steeper and it is easier for particles to move toward the slanted side than toward the steeper side,so on average particles move to the right(positive average velocity). It is important to note that in the overdamped limit current reversals of the non-active particles can be induced by several combined rectification mechanisms in complex systems.[42,43]However,in our simple system,the ratchet effect only occurs in a single direction when the inertia is neglected.

For the underdamped case(with the inertial term)shown in Fig.2(a),the transport behaviors become complex. For the certain value ofα, upon increasingf0, the average velocity firstly increases to its negative maximal value,then decreases,and finally reverses its direction. The most important feature for the underdamped case is the occurrence of current reversal.This phenomenon is also a common feature in collectively interacting non-active systems,[44-46]where the reversal mechanism is different from that in the present system.

Now we will explain the above behaviors. The direction of transport is determined by the competition between the slope of the structure and the distance from the lowest to the highest part of the asymmetric structure. When the distance from the lowest to the highest part of the asymmetric structure dominates the transport(particles can easily pass the barrier),and the distance from the slanted side is longer than the steep side, the particles are easily thrown out from the steep side,resulting in negative average velocity. As shown in Fig.2(e),most of the particles are concentrated on the steep side; thus,on average the average velocity is negative. Asf0increases,the effect of inertia weakens; the slope of the structure dominates the transport (particles cannot easily pass the barrier),and the left side of the asymmetric structure is steeper and thus particles prefer to gather on the slanted side(see Fig.2(f)),resulting in particles on average moving to the right. Of course,if the structure is negligible, the ratchet effect will disappear.Note that the direction of the particles also depends on the magnitude ofα; please refer to Fig. 5 for a specific explanation. For a very large value ofΓ(e.g.,Γ=30.0), shown in Fig. 2(c), the system reduces to its overdamped version and thus the curves are almost identical for both underdamped and overdamped cases.

In Fig.2(d),we plot the average positionxof particles as a function of the timetstarting from the random initial condition for various valuesf0,corresponding toa,b,cin Fig.2(a).Ataandb,|x| increases over a long period of time, which means that particles continuously flow in the right(or left)direction near the optimal valuef0. Atc,xis near zero for a long time, illustrating that the directed transport is destroyed for largef0.

The dependence of the average velocityvon the friction coefficientΓfor various valuesαare presented in Fig. 3. In the underdamped regime, at short timescales (t ≪1/Γ), the dynamic of particles is dominated by inertia and the trajectory cannot be self-similar, which is termed “ballistic Brownian motion”.[47]In the overdamped regime, particles show diffusive motion at short timescales.[48]According to Eq.(7),there exists competition between the friction coefficientΓand the self-propelled forcef0. This means that at small values ofΓ, the self-propulsion force plays a key role in transport and thus the average velocity is prominent.WhenΓ →∞,the selfpropulsion force is completely suppressed and rectification is destroyed,thusv →0. However,for intermediate values ofΓ(e.g.1.0＜Γ ＜10.0)and desirable values off0(e.g. f0=0.5 see Fig.3(a)),the distance from the lowest to the highest part of the asymmetric structure dominates the transport; the particles are easily thrown out from the steep side and thus the average velocity is negative. However,for the case off0=2.0[see Fig.3(b)],the slope of the structure dominates the transport;the average velocity is always positive and there exists an optimal value ofΓat whichvis maximal.

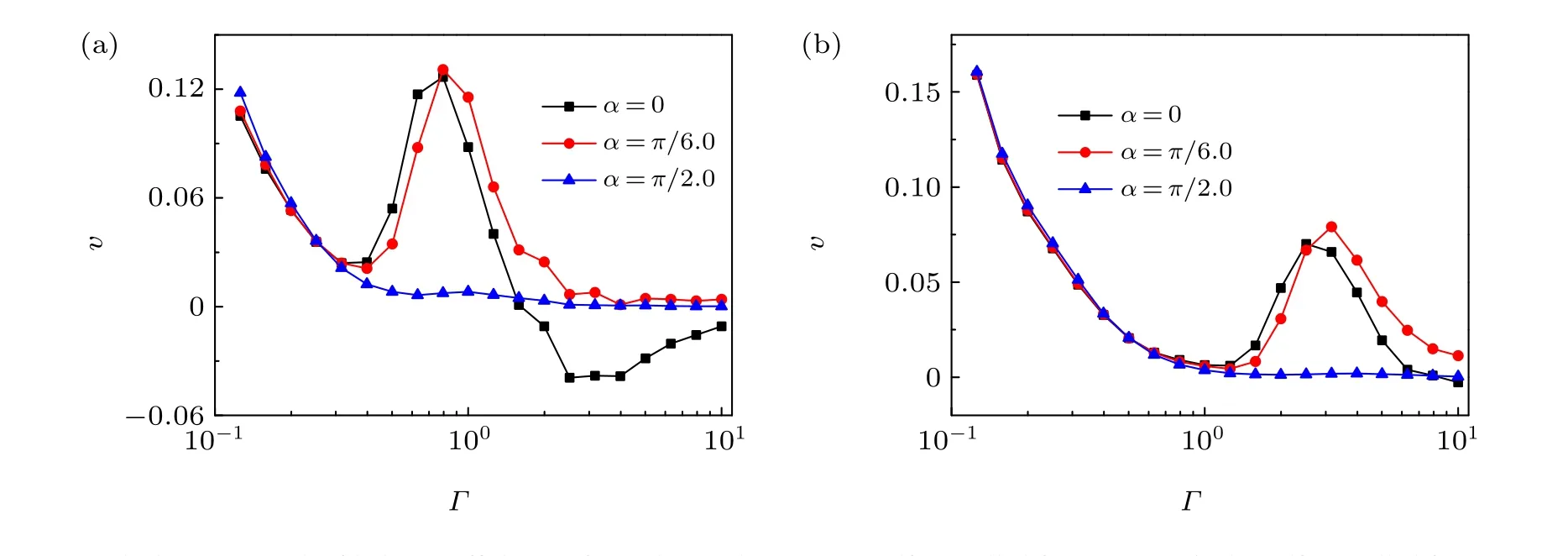
Fig. 3. Average velocity v versus the friction coefficient Γ for various values α. (a) Self-propelled force f0 =0.5. (b) Self-propelled force f0 =2.0. The other parameters are Dθ =0.01,W =3.0,ρ =1.5,and g=0.1.

We present the average velocityv versusthe polar interaction strengthgfor variousαin Fig.4. When the polar interaction is considered, particles show clustering behaviors. Note that the size of the cluster increases with polar interaction strength.Wheng →0,the polar interaction can be ignored and particles cannot form a cluster. Asgincreases,the polar interaction takes effect and particles form some clusters. Also,the clusters begin to interact with asymmetric structures. For the case off0=0.5,shown in Fig. 4(a), particles are very sensitive to the distance from the lowest to the highest part of the asymmetric structure and particles can be easily thrown out from the steep(left)side,resulting in negative average velocity. For the case off0=2.0,shown in Fig. 4(b), the slope of the structure dominates the transport and thus the average velocity is always positive. Wheng →∞,all particles form a big cluster and the effect of asymmetric structures is negligible;the ratchet effect will disappear and thusvreduces to zero. The corresponding polar order parameterPas a function ofgis plotted in Fig.4(c). Because the polar interaction dominates the transport,particles move in the same direction and form a big cluster(see Fig.4(d)),leadingP →1.

Fig.4. Average velocity v versus the polar interaction strength g for various values α at Γ =3.0. (a)Self-propelled force f0=0.5. (b)Self-propelled force f0 =2.0. (c) Polar order parameter P as a function of the polar interaction strength g for various values α at Γ =3.0 and f0 =2.0. (d) Representative trajectories of particles(different particles are differentiated by color)moving inside the channel at g=21 and α=0.0 described by a in panel(b). The other parameters are Dθ =0.01,W =3.0,and ρ =1.5.

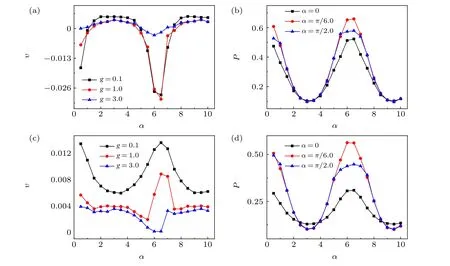
Fig.5. Average velocity v and polar order parameter P versus the phase lag α for various values g at Γ =3.0. (a)and(b)The self-propelled force f0=0.5.(c)and(d)The self-propelled force f0=2.0. The other parameters are Dθ =0.01,W =3.0,and ρ =1.5.

Figures 5(a)and 5(b)show the average velocityvand polar order parameterPover the phase lagα. Forα=0, we can feature the phenomenology of the Vicsek model. In this model,two solutions are possible: one observes the formation of the polar order when the noise is small, whereas particles exhibit disordered motion.Due to the current value of the rotational diffusion coefficientDθ=0.01,our system satisfies the former scenario. In this case (α=0.0), particles form some clusters andPattains a maximal value,shown in Figs.5(b)and 5(d). The presence of the phase lag causes the synchronized particle system to start rotating(see the trajectory of the particles in Fig.6(a)),which suppresses the rectification and polar strength. Therefore, both the average velocity and the polar order decrease. The introduction of phase lag can be considered as a substitution of chirality explicitly by the rotation frequency of each particle.[37,49,50]In addition,when we perform analysis of the right-hand side of Eq. (9), it is found that the term ofαhas a periodic effect on the rectification. Thus, the above discussion is valid only based on the minimum period regime ofα.

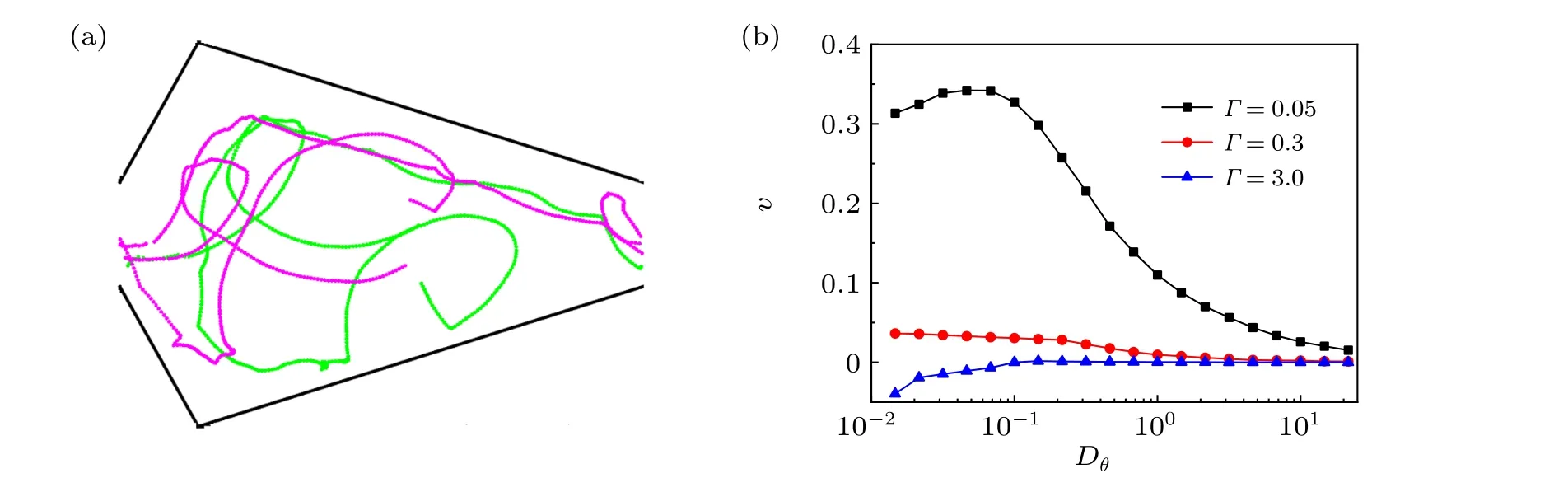
Fig.6. (a)Representative trajectories of particles(different particles are differentiated by color)illustrate the underlying mechanics between α and the polar interaction: for large α (α=π/2.0),particles follow circular orbits and frustrate the polar interaction. The other parameters are g=1.0,Dθ =0.01,ρ=1.5,W =3.0,and f0 =2.0. (b)Dependence of the average velocity v on the rotational diffusion coefficient Dθ for various values Γ. The other parameters are f0=0.5,g=0.1,α =0.0,W =3.0,and ρ =1.5.

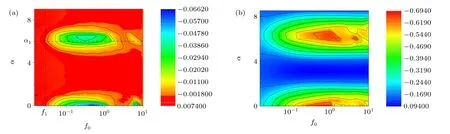
Fig. 7. (a) Contour plots of v as a function of f0 and α. (b) Contour plots of P as a function of f0 and α. The other parameters are Dθ =0.01, g=0.1,Γ =3.0,W =3.0,and ρ =1.5.

Figure 6(b)depicts the impact of the rotational diffusion coefficientDθon the rectification of self-propelled particles.The correlation function of the orientation is expressed as〈n(t)·n(t＇)〉=e-Dθ|t-t＇|.[51]WhenDθ →∞, this correlation converts to the delta function, the persistence length decreases(eventually vanishes)and the self-propelled force acts as a zero mean white noise;thus,the system is in equilibrium and the rectification disappears. WhenDθis small,the curvesv(Dθ) are different for two cases: (A) for the damping case(e.g. Γ=0.3,3.0) and (B) for the weak damping case (e.g.Γ=0.05). For the damping case(Γ=0.3,3.0),the momentum relaxation timeτ=1/Γis far less than the persistence timeτp=1/Dθ=100. Thus, rotational diffusion dominates the transport;this case is similar to the adiabatic regime in the forced thermal ratchet.[52]This means that the self-propelled angleθiremains nearly the same and the average velocity approaches its maximal values. For the weak damping case(e.g.Γ=0.05), the momentum relaxation timeτbecomes large,and the damping process competes with the rotational diffusion. When increasingDθfrom zero, the thermal noise, by pulling the particles towards the channel,acts as lubricant and thus the average velocity increases. WhenDθ →∞, the system begins Brownian motion and becomes homogeneous,thus suppressing the rectification.

To investigate the dependence ofvandPonαandf0in detail, we show the contour plotsvandPas a function ofαandf0in Figs. 7(a) and 7(b). By adjustingf0andα, the curves ofvandPchange periodically. Whenαis increased from zero, the average velocity is always positive atf0＜f1;interestingly,in the period range ofα ∈[0,2π](0＜α ＜α1),the particle changes its direction twice atf0＞f1. The critical values off1andα1depend on the system parameters.

4. Conclusion

In this work, we have numerically studied the ratchet transport of underdamped particles subject to phase lag in a 2D asymmetric channel. We found that when the inertial term is included,the transport behaviors become complex.For very small values ofΓ, the average velocity is always positive.For intermediate values ofΓ,the average velocity is negative for a small self-propelled force and positive for a large selfpropelled force. For very large values ofΓ, the system can be reduced to an overdamped version. In addition, there exists an optimal value of the polar interaction strength at which the rectification is maximal. We have shown that it is possible to change the direction of the particles in the presence ofα.On increasing the phase lag from zero, the average velocity can change its direction serval times for characteristics of criticalf0. Moreover,by introducing the phase lag,particles start to rotate and might suppress the rectification. For the damping case, the average velocity decreases monotonously with increasingDθ;however,for the weak damping case,there exists an optimal value ofDθat which the average velocity is maximal.

Acknowledgments

Project supported by the National Natural Science Foundation of China (Grant No. 12075090), the Key-Area Research and Development Program of Guangdong Province,China (Grant No. 2019B030330001), the Science and Technology Program of Guangzhou City(Grant No.2019050001),the Natural Science Foundation of Guangdong Province,China (Grant No. 2017A030313029), and the Major Basic Research Project of Guangdong Province, China (Grant No.2017KZDXM024).