基于PCA的火电厂电气设备故障诊断方法

聊方伦,周 平

(1.安徽安庆皖江发电有限公司，安徽 安庆 246008；2.浙江浙能嘉华发电有限公司，浙江 平湖 314201)

1 引言

我国工业技术快速发展，相对应的生产装置也呈现出大型、高效以及自动化趋势发展。在现实应用中相关用户对设备要求也在不断提升，在保证设备高效节能的同时，还需要保证设备在正常运行中减少故障产生，但由于大多数电气设备都是高科技产品，在实际运用中难以避免出现故障问题。诊断技术一般是在设备正常运行状态下，寻找出运行出现异常的地方，并根据故障数据判定相对应的解决对策，以此完成诊断。诊断的目的是在可以保证人员安全的同时，尽量减少因故障产生的影响，也是为了保障设备的基本安全，延长其使用寿命，从根本上提升设备生产效率，获取出最大化的经济效益。

黄葆华等人利用SBM和FPSDG的优点，将两者融合得到基于SBM-FPSDG 的设备故障监测诊断方法，以高压加热器为研究对象，利用其历史运行数据建立SBM模型，根据设备运行特性建立了故障单元库和概率，可以实现高压加热器监测及故障诊断[1]。周璐婕等人提出一种基于反向传播BP 神经网络的车载设备智能故障诊断方法。为了避免主特征信息的冗余，采用主成分启发式属性约简算法进行降维降噪。另外，由于BP神经网络对初始权值比较敏感，采用遗传算法对BP神经网络的初始权值和阈值进行了优化[2]。

虽然上述两种方法最后可以实现故障诊断，但由于该方法并不会针对故障特征提取分析，所以会出现计算量大的问题，因此本文提出基于PCA的火电厂电气设备故障诊断方法。PCA(principal component analysis，主元分析)作为一种不依赖于系统数学模型的建模方法，它可以将多个相关变量同时转化为几个不相关的变量，为火电厂电气设备故障诊断提供一种新的途径。引用BP神经网络与遗传算法相结合的诊断方法，利用其参数及结构完成诊断。

2 PCA下火电厂电气设备故障诊断

2.1 PCA主元数量确定

该方法可以根据不同的正交向量，让计算过程中的数据变化呈现在向量方向中，以便获取出传感器数据之间的相关性[3]。

首先在电气设备正常运行时，选取出一段传感器采集数据，并把数据构成数据矩阵，在矩阵集合中将n和m描述为采样点数以及传感器数量。为了能够有效除掉因量纲不同带来的不合理影响，便需要对进行标准化计算，获取出对应数据集合，构建PCA 的过程统计模型如下所示：

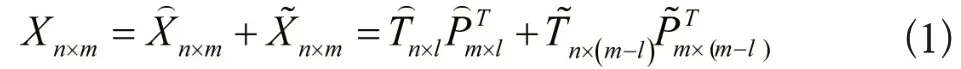
计算结果的主元数量精准程度，可以直接影响到后续步骤的实际取值结果，所以创建系统主元模型中，需要以确定主元数量为基本前提，此处本文采用最优重构法[4]，通过下列计算确认构建其模型的主元数量。该方法定义不可重构方差为：

根据上式计算结果可以明显看出，uj的取值结果与有明显的关系，而则和计算主元个数有着直接联系。为了可以在每个故障数据方向上都能实现重构计算，本文根据下式计算结果，挖掘出可以符合其所有条件的主元个数来判定是否为最优重构，有：

式中将a和l分别描述为计算中可能发生变化数据的数量以及实际存有的主元数量。通过计算不同的主元个数，即可分别获取出uj，这样即可得知选取与其结果相对应的主元数量为最优主元数。

根据上式计算结果以及主元数据的所有投影，把最开始m个数据变量降低到目前这些l 个主元，l 维的主元空间便替换的之间的m维过程数据空间，还会除掉两个空间之间的相关性[5]。

2.2 故障特征提取

结合上述计算分析，采用PCA 对故障特征数据提取降维计算过程如下：

(1) 原始数据标准化：

根据上式计算结果，即可获取出新的标准化矩阵：

(2) 构建相关矩阵，求解特征取值与向量

根据上述计算可得知，PCA 不仅可以减少后续计算的次数，而且可以提高整体性能[6]。

2.3 基于BP神经网络和遗传算法的故障诊断

经过上述计算得知，BP神经网络在电气设备故障诊断过程中，极为容易出现误差，导致后续诊断失误情况，因此本文提出遗传算法与BP 神经网络相结合。其基本运算过程如图1所示。

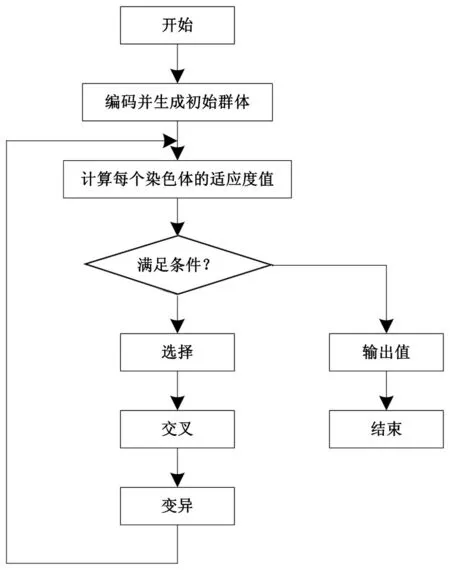
图1 遗传算法流程图

遗传算法以及BP 神经网络都是基于生物学原理研究的数学计算方法，本文在诊断故障设备的过程将其结合，是为了能够从中获取出两种算法不同优点，在有效诊断的同时，得出有效的解决途径[7]。

在实际计算过程中，首先利用遗传算法对BP网络中的结构及参数进行优化处理，从而获取出最优取值的网络结构、初始权值、阈值以及学习速率。

2.3.1 结构与算法过程

计算过程中可以将BP 算法分为正向传播、反向传播，其工作过程如下：在正向传播中，样本从输入层通过所有隐藏层传输到输出层，在输出层比较当前输出和预期输出。如果满足误差要求，则完成计算；如果不满足，则进行反向传播[8]。

在正向传播计算过程中，首先需要将数据样本从输入层转换到输出层，转到输出层之后将目前计算结果和实际期望取值进行对比，经对比结果得知，如果符合误差条件要求，那就结束计算，如果不满足，则执行反向传播；再现将返回一个错误信号，并修改单个神经元阈值以将误差最小化[9]。

其中具体计算流程如下述：

第一步：选取出合适的输入样本Xk和目标样本Tk，并将其代入至神经网络计算中；

第二步：正向计算。正向计算过程中分别将输入层第i个神经元输出以及第h个神经元输出表示为：

第三步：计算输出层第i个神经的输出以及输入

第四步：求解输出误差

第五步改善输出层、隐含层的全部阈值、权值：

第六步：计算BP神经网络总误差

第七步：判断是否达到预定的培训时间，如果符合条件则结束训练，反之，返回步骤二继续训练。

2.3.2 隐层节点数和学习速度确定

由于神经网络的隐层节点数和学习速度是由实验测试确定的，所以在确定隐层节点数时，学习速度为0.1。对5-10 个隐层节点的BP 网络进行了10 次全训练，分别计算了平均运行长度和训练转化率。表1列出了不同隐层节点的BP网络的平均转换阶段数和平均工作时间，即10个培训班的培训专业数[11-12]。

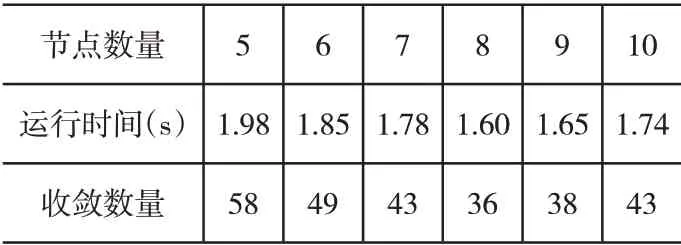
表1 不同隐含层节点数的平均收敛次数及运行时间

由表1可知，当隐层节点数为8 时，网络收敛速度较低，工作时间较短，无故障训练。因此，神经网络层BP的隐节点数被定义为8个。

由表2可知，当网络中的学习率为0.1-0.3 时，网络中的收敛阶段数较少，工作时间也较短，且无训练失败。在此之后，BP神经网络的学习速度为0.15。

表2 不同学习速率的平均收敛次数及运行时间

2.3.3 故障诊断输出

其中具体计算流程如下：

步骤一：遗传算法中的每个种群集合都将代表BP网络中的一个结构及参数；

步骤二：保持在数据初始状态下，构建BP神经网络；

步骤三：BP 网络输入层中输入一组遗传数据样本，并利用遗传样本训练，获取出神经网络的输出误差取值；

步骤四：根据上一步进行检测，查看是否有遗漏没有计算的样本，如果没有则将步骤三的取值，将其看作为适应度函数，然后分别计算每个样本的适应度取值；

步骤五：针对遗传算法中的数据交叉可能性进行计算，利用交叉以及突变的遗传方法产生新的种群；

步骤六：根据步骤五的结果，若是不符合下一步骤的条件则转为上述步骤三，符合条件下一步；

步骤七：结束遗传基本，计算出目前每个数据集合的适应函数取值，并在众多取值中选取出最高值，看为最优单位。根据数据单元解码计算，获取出最优神经网络结构、初始权值、阈值以及学习速率，并根据其结果构建最优神经网络。

步骤八：最优BP 网络中输入层采样一组数据样本，计算得出训练网络的实际输出；

步骤九：再次检测数据是否经过训练计算，如果没有返回步骤八；

步骤十：计算误差与实际是否差距过大，若是满足E＜σ条件就可以结束训练计算[13-14]。

在实际应用中本文根据编码方式随机产生含有80个个体的初始群体，每个个体的编码长度为25+((8×25+25×4+25+4)+1)。其中，前面的是25 个是连接基因，采用二进制编码方式，每个个体初始化为0 或 1；后面的((8×25+25×4+25+4)+1)个是参数基因，采用实数编码方式。其中，(8×25+25×4+25+4)个是权阈基因，初始化为(-1，1)的实数，最后的一个是速率基因，初始化为(0，1)的实数。

3 仿真实验

为了能够进一步验证本文方法的有效性，将在实际仿真环境中，对电气设备中的轴承进行故障诊断验证。一般情况下大型电气设备轴承是比较容易出现故障的地方，所以在实际仿真中采用对轴承对的检测来进一步验证本文方法的实际有效性，以及检测故障的诊断能力。

实际仿真数据采用某数据库提供的轴承故障数据集合，然后将其分为三种，分别是外圈故障、内圈故障以及滚珠故障。从三个数据集合中分别抽取出1500 个样本，其中1000个样本进行训练，另外500个用于测试。

诊断过程中分别为将本文方法与文献方法[1]、[2]进行诊断精准度对比，其中对比结果如下表所示。

表3 故障诊断准确度对比表/%

从上表中即可看出，与文献方法相比，本文方法在三种故障方面都具有较高的诊断率，由此可得知本文方法所使用的PCA进行故障特征提取时，具有较大的优势。

将网络诊断实际输出和期望输出进行对比，输出结果如图2所示。其中神经网络隐含层节点数、收敛步数、学习速率以及网络误差分别设置为13、9、0.182以及0.048。

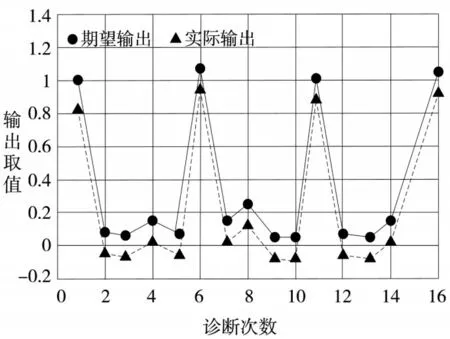
图2 故障诊断输出对比图

从上述图2可以看出，本文算法输出结果与实际值相差极小，同时图3能够看出，本文算法经过多次计算，误差都能有效保持在0.1之下，获得的结果误差在实际运用过程中可忽略不计，可广泛使用。

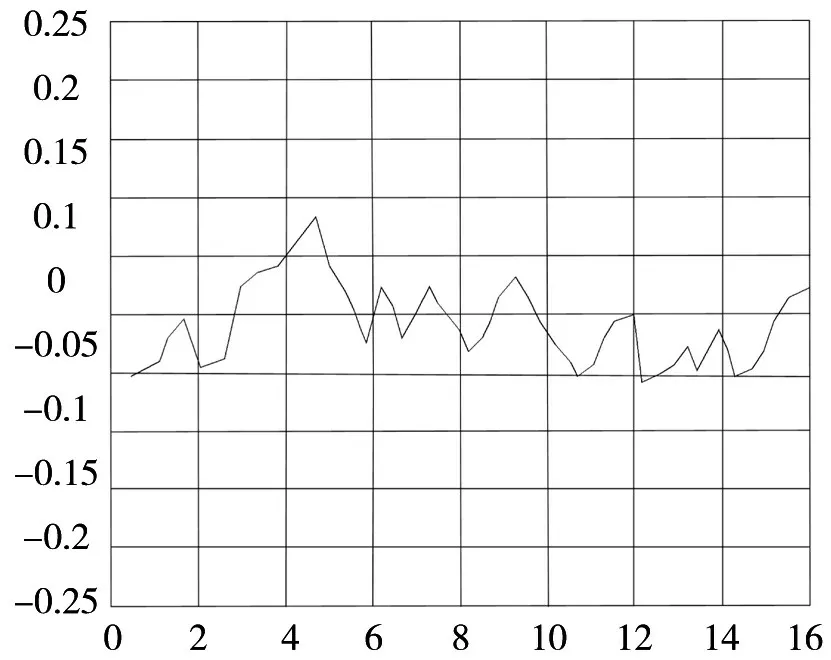
图3 故障诊断误差曲线图

4 结束语

由于电气设备故障诊断方法，容易出现因故障特征提取困难导致诊断失误等情况，本文提出基于PCA的火电厂电气设备故障诊断方法。根据PCA算法计算得知相关性，确定主元数量，并构建主元分析模型，随后采用BP神经网络进行故障诊断，计算中发现BP用于诊断会出现隐含层节点数难判定的情况，基于此本文采用GA+BP相结合算法，构建合适的网络结构进行诊断。虽然可以有效解决其缺陷，但在故障提取计算中，需要严谨的计算，因为主元数量一旦有差异，那么后续步骤都会失误，所以仍有待优化。