基于改进型SMO的PMSM无传感器鲁棒控制方法

王丽 高远 袁海英

摘  要：为提高永磁同步电机无传感器控制系统的控制性能和抗干扰能力，提出一种改进型滑模观测器无传感器鲁棒控制方法。该方法引入双曲正切函数替代传统滑模观测器的开关函数，并采用锁相环技术对转子状态信息进行提取，以削弱观测器的抖振效应和提高转子状态估计精度;为抑制转子状态估计误差和不同负载工况等干扰，提高无传感器控制系统的整体性能，设计速度环自抗扰控制器来替代传统的PI调节器。控制系统仿真结果表明：相比传统方法，该方法不仅能有效抑制抖振，提高转子状态的估算精度，而且进一步提高了电机无传感器转速跟踪控制的性能和鲁棒性。

关键词：永磁同步电机;改进型滑模观测器;自抗扰控制;鲁棒性;估计精度

中图分类号：TM351           DOI：10.16375/j.cnki.cn45-1395/t.2022.02.007

0    引言

近年来，永磁同步电机（permanent magnet  synchronous motor，PMSM）调速系统广泛应用于纯电动汽车、机器人、工业传动等领域。PMSM控制系统普遍采用机械式传感器检测反馈电机的转子状态（速度和位置）信息，这不仅增加系统设备的安装维护成本和体积，而且传感器检测效果易受电磁、温度等因素干扰，对电机调速控制性能造成不良影响，甚至会出现传感器故障，导致控制系统失稳等问题[1]。为提高PMSM调速控制系统的容错能力，近年来，PMSM无传感器控制技术备受关注。针对PMSM无传感器控制问题，提出了扩展卡尔曼滤波方法、模型参考自适应方法、滑模观测器（sliding mode observer，SMO）方法等[2-4]。

传统的SMO方法采用不连续的滑模面切换开关控制函数，使得PMSM转子状态估计存在抖振效应，导致转子状态观测精度降低[5]。为抑制或降低滑模抖振效应，提高转子状态估计精度和无传感器控制效果，有学者采用准滑模函数思想，在SMO中引入饱和函数或分段指数函数等具有连续性的切换函数来替代传统的符号开关函数[6-7]。文献[8]采用低通滤波加相位补偿的方法滤除高频抖振，同时对滤波导致的相位延迟进行补偿，然而该方法固定的滤波器截止频率和相位补偿环节无法适用于大范围调速且负载变化的无传感器控制情形。近年来，有报道采用截止频率可变的滤波器或级联滤波器等对观测器输出进行高频抖振滤波，虽能滤除高次谐波和减小相位偏差，但截止频率和相位补偿值的调节律设计使方法变得复杂，计算量变大[9-10]，且还存在相位延迟的补偿环节情况[11]。

现有的PMSM无传感器控制系统大都采用速度环、电流环的双闭环比例积分（proportional integral，PI ）矢量控制，虽然PI控制器结构简单，但自适应能力不强，控制效果易受到估计误差、系统参数、外部负载等摄动干扰的影响，无法获得令人满意的电机控制动静态性能及鲁棒性[12]。近年来，有学者在探寻高精度鲁棒观测器，同时也对PMSM的速度环开展先进控制算法研究，提出了速度环的积分滑模控制[13]、模糊PI控制[14]、分数阶滑模控制[15]等方法，旨在提高无传感器控制系统的整体 性能。

为提高基于SMO的PMSM无传感器调速控制系统的整体性能和鲁棒性，本文设计一种改进型SMO，通过采用连续光滑的双曲正切函数代替传统SMO中不连续的开关函数，以有效抑制观测器输出的抖振效应。考虑双曲正切函数输出的连續性，为降低观测器输出延迟和误差，省去传统SMO中的低通滤波器环节，引入锁相环技术（phase-locked loop，PLL）替代反正切函数求解运算来提取估计反电动势中的转子状态信息。此外，鉴于线性自抗扰控制器（linear active disturbances rejection controller，LADRC）是一种鲁棒性控制器，设计速度环LADRC 替代传统的转速环PI控制器，以有效抑制时变负载及系统参数摄动、估计误差等扰动对PMSM无传感器转速控制性能的不良影响，提高控制系统的整体性能。改进型SMO的PMSM无传感器鲁棒控制系统的仿真对比结果验证了工作的有效性。

1    PMSM的数学模型

考虑两相定子绕组电感大小相同的表面贴式PMSM，其在α-β静止坐标系下的定子电流方       程为[16]：

[diαdt=-RsLsiα+1Lsuα-1Lseα，diβdt=-RsLsiβ+1Lsuβ-1Lseβ.]             （1）

式中：[iα]、[iβ]分别表示定子在[α]、[β]轴上的电流分量，[uα]、[uβ]分别表示定子在[α]、[β]轴上的电压分量，[Rs]和[Ls]分别是定子绕组的电阻和电感，[eα]、[eβ]分别为[α]、[β]轴上的反电动势分量，并满足如下方程：

[eα=-φfωrsinθ，eβ=φfωrcosθ.]                   （2）

其中：[φf]为永磁体磁链，[ωr]为转子角速度，[θ]为转子旋转角度。

采用[id]=0的矢量控制方式，则PMSM在d-q坐标系下的机械运动方程为：

[dωrdt=32PnφfJiq-BJωr-TLJ]，              （3）

式中：[iq]表示[q]轴定子电流，[TL]为负载转矩，[Pn]为电机极对数，[J]和[B]分别代表转动惯量和阻尼系数。

2    PMSM转子状态的改进型SMO

PMSM转子状态的SMO方法的核心是设计恰当的定子电流滑模控制器，实现估计电流与实际电流间的误差为0，此时所观测得到的反电动势可视为真实的反电动势，通过制定有效的提取算法，从反电动势估计中获取转子状态信息[4-6]。

图1为PMSM的传统SMO原理结构框图[7]。图中，[iα]和[iβ]分别为定子在α、β轴上的估计电流分量，[eα0]和[eβ0]为含有高频抖振分量的反电动势估计分量，[eα]和[eβ]则表示反电动势估计分量。图1所示的传统SMO原理方案，由于采用符号开关控制函数，导致反电动势的高频抖振效应会干扰反电动势频谱，降低估计精度，对控制系统带来不良影响，所以这不仅需要低通滤波器对反电动势平滑滤波，而且还需增加相位补偿器对相位的滤波延迟予以补偿。转子位置信息通过arctan（.）函数进行提取，虽然简单，但这种开环提取方式存在较大误差。

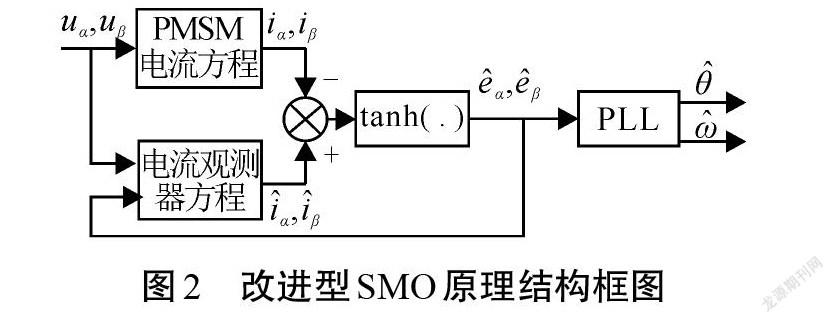
为获得连续的估计反电动势，降低或避免传统SMO不连续开关控制函数所导致的高频抖振效应，同时提高电机无传感器控制系统的转子状态观测精度和稳定性，本文利用准滑模的控制思想，引入双曲正切函数tanh（.）构建滑模控制律来获得连续的估计反电动势，在一定程度上可省去为抑制高频抖振而设置的低通滤波器及其后续的相位补偿环节，进而降低观测器的实现复杂度。为提高轉子状态估计精度，采用具有反馈结构的PLL技术，从观测的反电动势中提取出转子转速[ωr]和转角信息[θ]。本文提出的改进型SMO原理结构框图如图2所示。

定义定子电流估计误差向量[i=iα， iβT=iα-iα， iβ-iβT]，滑模面函数[S=i]。结合图2所示的原理，利用式（1）建立定子电流滑模观测器的状态方程：

[diαdt=-RsLsiα+1Lsuα-1Lseα，diβdt=-RsLsiβ+1Lsuβ-1Lseα.]              （4）

式（4）中反电动势估计[e=eα， eβT]，设计采用如下的连续切换滑模控制器函数表示：

[e=eαeβ=ktanh（S）=ktanh（i）=ktanh（iα）ktanh（iβ）]，       （5）

式中：[k]为滑模增益系数。

定义电动势向量[e=eα， eβT]，利用式（1）、式（4）和式（5）可得到电流的估计误差方程：

[didt=-RsLsi+1Ls（e-ktanh（i））].          （6）

建立如下的李雅普诺夫函数：

[V=12STS].                           （7）

对式（7）两边进行时间求导，结合式（6）可得：

[V=STdSdt=（i）Tdidt=-RsLs（i）Ti+（i）TLs（e-ktanh（i））≤] [-RsLs（i）Ti+1Ls（i）Te-ktanh（i）].     （8）

类似于文献[17]的证明方法，选择滑模增益系数[k]，当[ktanh（i）>e]时，如下的滑模面可达条件成立：

[V=STdSdt=（i）Tdidt≤0].                   （9）

根据滑模变结构控制理论，当误差系统在滑模面上运动时，能实现滑模面[S=i=0]， 以及[dSdt=didt=0]。此时，定子的估计电流和实际电流相等，式（5）的控制律逼近真实的反电动势。

图3为PLL技术从估计反电动势中提取转子转速和转角信息的原理框图。当[e→e]时，根据图3所示原理，并结合式（2）可以得到：

[Δe=（-eαcosθ-eβsinθ）→ωrφfsin（θ-θ）].   （10）

选择恰当的锁相环PI调节器参数，使得转角估计误差[θ-θ]较小时，式（10）可等效为：

[Δe=ωrφf（θ-θ）].                   （11）

3    速度环LADRC的设计

自抗扰控制是一种鲁棒性控制方法。为抑制电机负载、参数时变以及电机转子状态估计误差等扰动对PMSM无传感器控制系统的不良影响，提高转子状态观测器与速度环调节器的整体系统性能，使系统获得较高精度的转子状态鲁棒观测和较高的转速调控性能及抗干扰能力，降低控制器的结构复杂程度，本文设计一种不含跟踪微分器环节的一阶LADRC来替代传统的转速环PI调节器。因此，该LADRC主要由线性扩展状态观测器和线性误差反馈控制律两部分构成。

考虑PMSM的系统参数变化、负载摄动以及转子状态估计误差等对电机转速的控制影响，结合线性自抗扰控制理论设计LADRC[18]。将机械运动方程式（3）改写成包含扰动项和控制项的形式：

[dωrdt=fωr， TL+bu]，                     （12）

式中：扰动项[f（ωr， TL）=-BJωr-TLJ]，控制项

[b=32PnφfJ]，[u=iq]。

用改进型SMO获得估计转速替代真实转速，可设计如下的线性扩展状态观测器对估计转速以及转速环所受扰动进行观测。

[e=z1-ωr，z1=z2-β1z1-ωr+bu，z2=-β2z1-ωr.]           （13）

式中：[z1]表示对估计转速[ωr]的扩张观测器估计，[z2]表示转速环扰动估计，[β1、β2]为转速环观测器增益。

根据上式，可求出线性扩张状态观测器的特征多项式[λ（c）]：

[λ（c）=c2+β1c+β2]，                    （14）

式中：[c]表示特征根。定义[ω0]表示线性状态观测器的期望带宽，并构建期望的特征多项式：

[λ∗（c）=（c+ω0）2].                    （15）

采用极点配置方法可设计出观测器的增益     系数：

[β1=2ω0，β2=ω20].                   （16）

為提高电机转速跟踪控制的动静态性能和鲁棒性，同时减少转速控制误差对SMO输出的不良影响，设计如下表达式的线性误差反馈控制律以获得抵消扰动后的速度环控制信号[u]：

[u0=kp（ω∗r-z1）-kdz2，u=-z2+u0b.]           （17）

式中：[ω∗r]为系统期望转速，[kp]和[kd]分别为误差反馈控制律的比例参数和微分参数。

选取转速闭环的带宽[ωc]和阻尼比[ξ]，可按如下公式计算获得线性误差反馈控制律参数：

[kp=ω2c，kd=2ξωc].                   （18）

在实际应用中，通常选取临界阻尼比[ξ=1]，[ω0=（5-10）ωc] 。根据式（13）和式（17），可得如图4所示的转速环LADRC结构图。

4    仿真结果与分析

根据图5所示的PMSM无传感器控制系统结构图，在MATLAB/Simulink环境下，将改进型SMO和转速环LADRC进行模块化程序实现，搭建PMSM无传感器控制系统仿真模型并开展仿真实验研究。仿真中，按表1所列数值设置PMSM的系统参数，选取滑模观测器滑模切换增益参数[k=300];选取转速环LADRC相关参数：[b=397]、[β1=8 600]、[β2=4 3002]、[kp=4302]、[kd=860];锁相环参数[kp1=50]、[ki1=0.1]。

为验证本文方法（改进型SMO+速度环LADRC）的有效性，仿真中考虑PMSM负载转矩突变、期望转速跳变和系统参数时变的不同运行工况，并对比传统方法（传统SMO+速度环PI调节器）的无传感器控制效果。其中，传统方法转速环PI调节器参数为[kp2=0.9]、[ki2=0.6]。

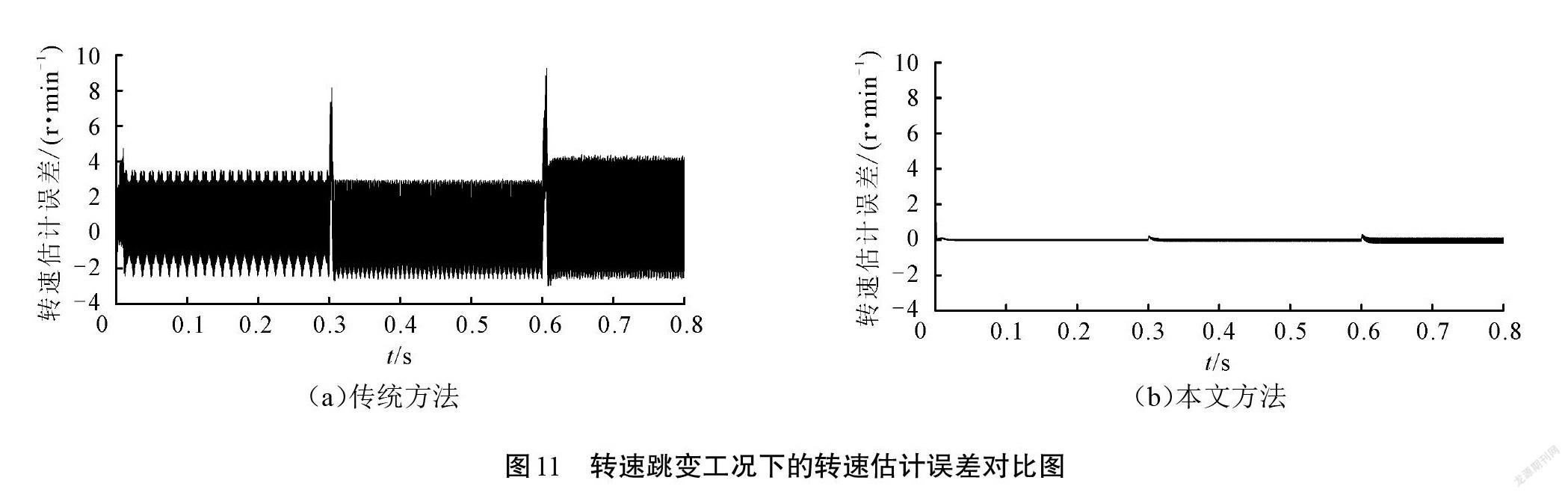
假定电机等效电阻R发生20%范围内的随机波动，考虑PMSM期望转速[ω*r]=1 000 r/min，启动负载转矩TL=1 N·m，在0.4 s时由TL= 1 N·m跳变至  TL=8 N·m的负载突变运行工况，图6—图8分别为负载突变工况下的实际转速曲线、估计转速曲线和估计误差曲线。并考虑在0 s、0.3 s、0.6 s时期望转速[ω*r]分别取300 r/min、600 r/min、1 000 r/min的变速运行工况，图9—图11分别为该变速工况下的实际转速曲线、估计转速曲线和估计误差曲线。

通过图6、图7和图9、图10的仿真结果曲线可以看出，即使在电机电阻参数时变、负载突变和变速的电机运行工况下，传统方法和本文方法都可对电机转速进行有效估计，均能实现转速对期望转速的稳定跟踪控制。但是，相比于传统方法，本文方法具有更好的无传感器控制效果，表现为启动或转速增加跳变节点均无超调，负载突变时仍具有很好的跟踪控制性能。同时，通过图8和图11的估计误差曲线可以看出，即使在负载突变、不同期望转速和电阻参数时变的情况下，本文方法都能实现对转子转速更为精确的观测，相比于传统方法，本文方法估计误差的抖振变化幅度明显降低。这表明：本文方法一方面通过设计改进型SMO以降低高频抖振效应和提高转子状态观测精度;另一方面设计速度环LADRC以抑制扰动对无传感器控制性能的不良影响，使得整个PMSM的无传感器控制系统的转速输出性能和鲁棒性得以整体提升。

5    结论

本文为提高基于SMO的PMSM无传感器调速控制系统的控制性能和鲁棒性，从提升电机无传感器控制系统整体性考虑，提出一种将改进型SMO与速度环LADRC相结合的控制方法。改进型SMO采用连续光滑的tanh（.）函数代替不连续的开关函数sgn（.），通过获得连续变化的反电动势估计来抑制滑模切换的高频抖振效应，与传统SMO相比，减少了低通滤波器环节和相位补偿环节;同时采用具有反馈结构的锁相环技术提高转子状态信息估计的准确性。速度环LADRC主要消除电机负载转矩变化和转速估计误差等扰动对电机转速跟踪控制性能的不良影响，以及确保在变速工况、负载跳变和系统参数时变的情况下SMO仍实现对实际转速的快速准确估计。不同电机运行工况下的PMSM无传感器控制系统仿真对比结果验证了所提出方法的有效性。本文采用速度环LADRC替代传统PI控制方法虽增加了控制器的运算复杂度，但通过改进SMO来避免传统方法中低通滤波器和相位补偿环节的滞后作用，从而平衡满足整体系统对算法的实时性要求，使系统的整体性能获得较好的提升。因此，利用现今的高速微处理器技术对该控制方法进行ECU系统开发，具有较强的实际应用可行性。

参考文献

[1]     刘计龙，肖飞，沈洋，等. 永磁同步电机无位置传感器控制技术研究综述[J].电工技术学报，2017，32（16）：76-88.

[2]     洪帅，高远，张银，等.基于SRUKF的永磁同步电机无传感器控制研究[J].广西科技大学学报，2019，30（1）：46-51，66.

[3]     高远， 刘传国，文家燕，等. 基于分数阶自适应转速估计的永磁同步电机无传感器控制研究[J].微电机， 2015，48（5）：85-89.

[4]     潘森林，高瑾. 永磁同步电机无速度传感器控制技术综述[J].微电机，2018，51（3）：62-69.

[5]     YUAN L， XIAO F， SHEN J Q，et al. Sensorless control of high-power interior permanent magnet synchronous motor drives at very low speed[J].IET Electric Power Applications，2013，7（3）：199-206.

[6]     GUO Z Q，PANDA S K. Design of a sliding mode observer for sensorless control of SPMSM operating at medium and high speeds[C]//2015 IEEE Symposium on Sensorless Control for Electrical Drives （SLED）. IEEE，2015.

[7]     张立伟，李行，宋佩佩，等. 基于新型滑模观测器的永磁同步电机无传感器矢量控制系统[J].电工技术学报，2019，34（S1）：70-78.

[8]     陈长龙，樊贝，胡堃. 永磁同步电动机新型滑模观测器无传感器控制[J].微特电机，2013，41（3）：44-47.

[9]     黃震，严彦，郑晨飞，等. 基于改进滤波器的无传感器永磁同步电机新型滑模观测器设计[J].电机与控制应用，2020，47（3）：28-33.

[10]   MURSHID S，SINGH B. An improved SMO for position sensorless operation of PMSM driven solar water pumping system[C]//2020 IEEE International Conference on Power Electronics，Smart Grid and Renewable Energy （PESGRE）. IEEE，2020.

[11]   高仁璟，李希伟. PMSM无传感器控制的新型滑模观测器设计[J].电机与控制应用，2014，41（11）：7-13.

[12]   于金鹏， 陈兵， 于海生，等. 基于自适应模糊反步法的永磁同步电机位置跟踪控制[J]. 控制与决策， 2010， 25（10）： 1547-1551.

[13]   袁帅，陈家新，周宇. 基于扩张状态观测器的改进型积分滑模结构设计[J].传感器与微系统，2021，40（6）：107-109.

[14]   郑飞，吴钦木. 基于模糊PI的永磁同步电机矢量控制[J].计算机与现代化，2021（1）：7-11.

[15]   缪仲翠，张文宾，余现飞，等. 基于转速估计的PMSM分数阶积分滑模控制[J].太阳能学报，2021，42（3）：28-34.

[16]   袁雷，胡冰新，魏克银，等. 现代永磁同步电机控制原理及MATLAB仿真[M]. 北京：北京航空航天大学出版社， 2016.

[17]   GAO Y，LIANG C H. A new 4D hyperchaotic system and its generalized function projective synchronization[J].Mathematical Problems in Engineering， 2013，2013：1-13.

[18]   韩京清. 自抗扰控制技术[M]. 北京：国防工业出版社，2008.

A sensorless robust control method based on

improved SMO for PMSM

WANG Li1， GAO Yuan*1，2， YUAN Haiying1

（1. School of Electrical， Electronic and Computer Science， Guangxi University of Science and Technology，

Liuzhou 545616， China;  2.Guangxi Key Laboratory of Automobile Components and Vehicle Technology （Guangxi University of Science and Technology）， Liuzhou 545006， China）

Abstract： A sensorless robust control method based on an improved sliding mode observer is proposed to improve the sensorless control performance and anti-interference ability of permanent magnet       synchronous motor. Firstly， the hyperbolic tangent function is used to replace the switching function of the traditional sliding mode observer.  Secondly， the phase-locked loop technology is also used to       extract the rotor state information so as to restrain the chattering effect of the observer and improve the estimation accuracy of rotor state. Then， an active disturbance rejection controller of speed-loop is      designed to replace the traditional PI controller so as to improve the overall performance of the         sensorless control system by reducing estimation errors and disturbance of different loading conditions. The simulation results of sensorless control system show that this method can not only suppress       chattering and improve the estimation accuracy of rotor state effectively， but also further improve the sensorless speed-tracking control performance and robustness.

Key words： permanent magnet synchronous motor; improved sliding mode observer; active               disturbance rejection control; robustness; estimation accuracy

（責任编辑：罗小芬）