基于溢流前缘长度变化的驼峰堰过流能力拟合
王洪俊
(中山市水利水电勘测设计咨询有限公司,广东 中山 528400)
1 前言
巴依托卡依渠首是一座拦河式渠首工程,主要建筑物包括泄洪冲沙闸、引水闸、溢流堰及上、下游河道整治段四部分。溢流堰堰面定型设计为驼峰堰,堰高1.5 m,堰长200 m,溢流堰防冲采用浆砌石斜坡式防冲。本次除险加固设计洪水标准为:P=3.33%,即30年一遇,设计洪峰流量为789 m3/s,闸前设计水位1269.80 m,此时泄洪闸通过流量735 m3/s,溢流堰通过流量54 m3/s。考虑到溢流堰堰顶高程,当水位低于堰顶高程,通过溢流堰的流量为0,水流全部通过泄洪闸下泄。对于开阔的平原地区,驼峰堰堰型选择不受地形条件限制,在低水头工况下,该堰型泄流能力较大,且结构简单,故应用范围较广。常用的驼峰堰过流能力计算方法很多,但是大多数计算方法均采用查图计算的方式,适用范围相当有限,对于地形陡峭的山区峡谷,驼峰堰堰型设计受到较大限制[1],无法直接套用现有泄流计算公式。
2 研究方法
为增大溢流前缘长度,以增加其过流能力,并降低堰顶水头,驼峰堰在平面上大多呈折线形布置。平原河道水库驼峰堰布置不受地形限制,能通过增大展长,充分利用其低水头工况下超大的泄流能力;而对于山区峡谷水库,因受地形限制较大,驼峰堰溢洪道控制数通常较少。
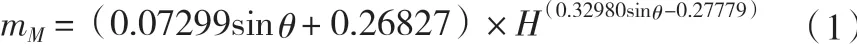
式中:mM为驼峰堰流量系数;H为堰顶水头,m; 为驼峰堰单峰角度,(°)。
上式中的流量系数取值随驼峰堰堰顶水头增大而呈减小趋势,能较好体现随水头增大驼峰堰水流流量持续增加的变动状态。进而可得出驼峰堰堰顶过流流量,公式如下:

式中:QM为驼峰堰模型堰顶过流流量,m3/s;bM为模型控制段设计宽度,m;HM为模型堰顶水头,m。
由式(1)所计算得出的驼峰堰流量系数其变动趋势与工程应用相符,并能体现出随水头增大,过堰水流流量随之增加的趋势特征,但是其过流能力计算结果和堰顶水头之间不满足Q=f(H1.5)的函数关系,且拟合过程中也出现了量纲不吻合现象,其在原型计算中应用时还必须按照几何比尺L放大处理,即将模型流量系数计算结果与几何比尺的0.2次方相乘,得到原型流量系数计算结果mp:

在以上分析过程中,均假定以模型控制段过流宽度为驼峰堰过流宽b,且不考虑实际泄流过程中随堰顶水头增加溢流前缘长度所发生的变化。
3 驼峰堰过流能力拟合
3.1 过堰水流流态
根据试验,驼峰堰过堰流态可划分为完全薄壁堰流、不完全薄壁堰流Ⅰ、不完全薄壁堰流Ⅱ、真空实用堰流等四个阶段。在较小流量工况下,水流流经驼峰堰峰头并贴侧堰壁下流时,侧堰水流表现为挑射状;流量增大后,侧堰水舌下缘逐渐出现空腔,并逐渐转移至下游峰头处,最后连接成带状和片状空腔;流量持续增大后,侧堰带状和片状空腔持续转化为小气泡移动至下游并最终完全消失。导致驼峰堰流量增大后侧堰水舌下缘出现真空的原因主要在于流量达到一定水平后,水流表现为实用堰流,但因驼峰堰水流长度较短,无法对堰水流施加顶托作用。
通过分析驼峰堰水流流态的变化,随堰顶水深增大,其溢流前缘实际长度L持续减小,其溢流前缘展长优势逐渐下降至控制段宽度b,其流态也逐渐从薄壁堰流转向真空实用堰流。通过分析原因发现,随水头增大驼峰堰过流能力不断降低的主要原因在于溢流前缘长度L持续减小。根据对驼峰堰水流流态变动趋势的分析,可借助薄壁堰流量计算公式(4)以及实用堰成果进行驼峰堰水流流态拟合。
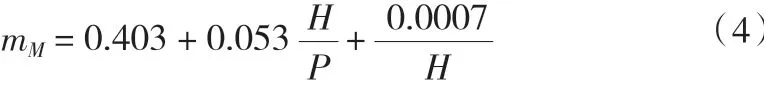
式中:P为驼峰堰堰高,m;其余参数含义同前。
3.2 过流能力
在驼峰堰单峰角度不同,但堰高及试验条件相同的情况下驼峰堰和实用堰过流能力试验结果见表1。

表1 驼峰堰和实用堰过流能力试验结果
3.3 溢流前缘长度拟合
在流量较小时,驼峰堰溢流前缘长度与实际溢流展长十分接近,而随流量持续增大,其长度逐渐减小,最终与控制段宽度相等。为此,可认为驼峰堰实际流量系数取值在薄壁堰和实用堰之间,故综合流量系数M表示如下:

也即,流量系数m和堰流前缘长度L以及堰顶水头H存在相关关系,可将式(5)变形为:

相关文献同时将驼峰堰溢流前缘长L表示为单峰角度的函数,具体如下:

式中:c为驼峰堰侧堰长,m;a为驼峰堰峰头长度的1/2,m。
根据现有的驼峰堰过流能力研究成果,将溢流前缘长度值代入堰流基本公式发现,在既定流量和水头下,流量系数与溢流前缘长度呈反向变动关系。通过薄壁堰流量系数公式及实用堰过流能力相关试验结果,可得出流量系数取值,具体见表2。表中试验结果代入驼峰堰堰流基本公式,便可计算出不同驼峰堰单峰角度试验方案下水头变化对应的溢流前缘长度值。
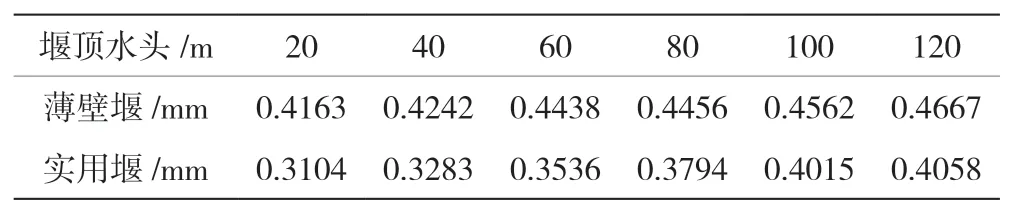
表2 流量系数取值
根据水流流态,进行驼峰堰溢流前缘长度与堰顶水头关系曲线的加密点绘,结果见图1。
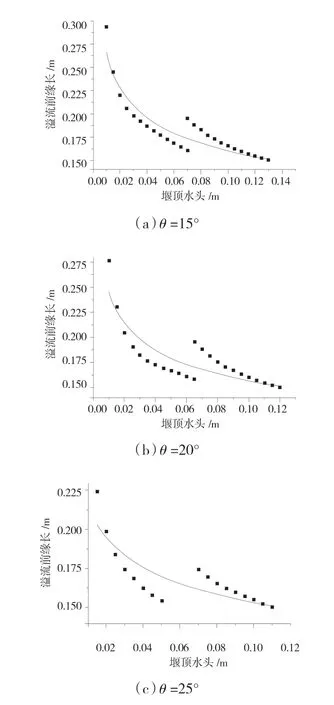
图1 驼峰堰溢流前缘长度与堰顶水头关系曲线
根据图1中所体现的溢流前缘长度与堰顶水头关系可知,薄壁堰溢流前缘长度与堰顶水头关系点位位于曲线左侧,而实用堰溢流前缘长度与堰顶水头关系点位则位于曲线右侧,两条曲线存在明显的分离,且单峰角度越大分离程度越明显。在曲线偏折处,水头相同情况下薄壁堰过流能力明显大于驼峰堰,薄壁堰所计算得堰流前缘长度值偏小;而实用堰过流能力则明显小于驼峰堰,实用堰所得堰流前缘长度值偏大。驼峰堰过堰水流流态变化是造成这种现象的主要原因,其单峰角度越大,水流过渡至实用堰的堰流也越早。
采用指数函数L=aoHbo进行驼峰堰溢流前缘长度与堰顶水头关系的回归分析,所得出的不同单峰角度下驼峰堰拟合结果具体见表3。
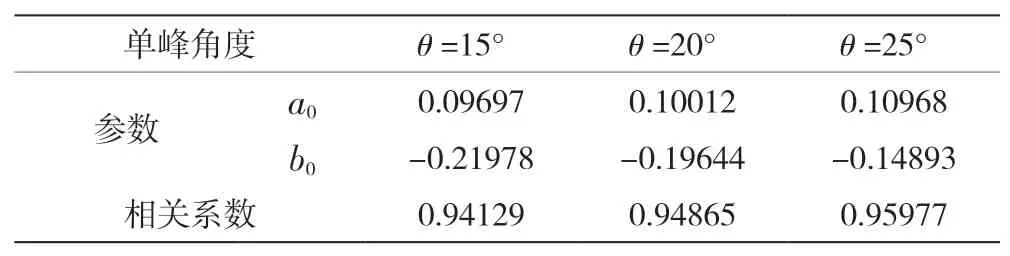
表3 驼峰堰溢流前缘长度与堰顶水头关系拟合结果
根据表3拟合结果,在不同单峰角度下驼峰堰溢流前缘长度与堰顶水头的相关系数均在0.94以上,且不同单峰角度对应的ao和bo取值存在差异,为此,进一步进行ao、bo及sin 的拟合分析,结果见图2。
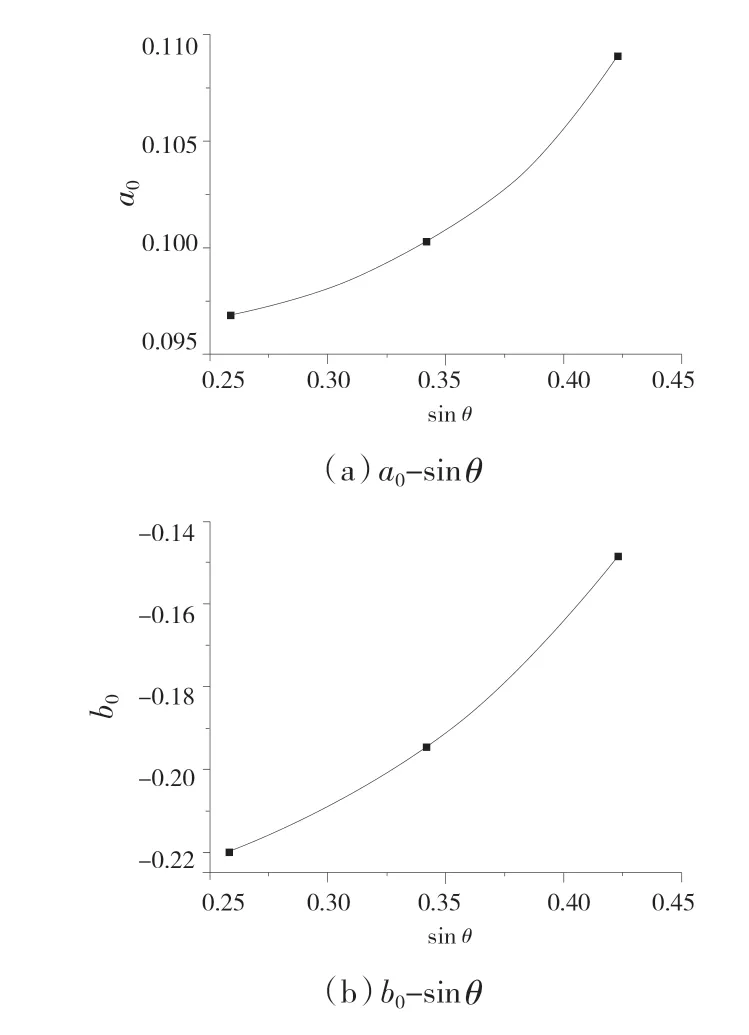
图2 a0、b0及sin 的拟合分析结果
根据结果可以看出,ao、bo及sin 等参数存在较高的相关性,故可以将ao、bo表示如下:

由此,可以得出驼峰堰溢流前缘长度的表达式,即:

式(10)为随水头变化的驼峰堰堰流前缘长度计算公式,据此便可得出不同单峰角度及堰顶水头条件下溢流前缘长度的拟合结果,具体见表4。
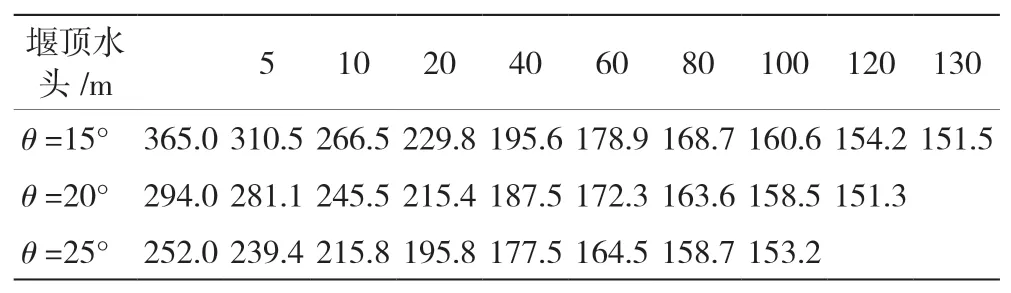
表4 不同单峰角度及堰顶水头条件下溢流前缘长度的拟合结果
流量较小时所得出的驼峰堰溢流前缘长与实际展长十分接近,而溢流前缘长度随堰顶水头的增大而不断减小,且待流量值达到一定程度后,驼峰堰便转变为真空实用堰,溢流前缘长及控制段宽取值完全一致,且不再变化。与此同时,在水头条件相同时,随着单峰角度的增大,驼峰堰从薄壁堰过渡至实用堰也更为容易[3]。
3.4 流量系数
在式(1)和式(2)的基础上,用溢流前缘长度形式表示过堰流量,公式如下:

由于流量相等,即Qm=QL,所以:mLL=mMbM,也即:化简后,流量系数可表示如下:
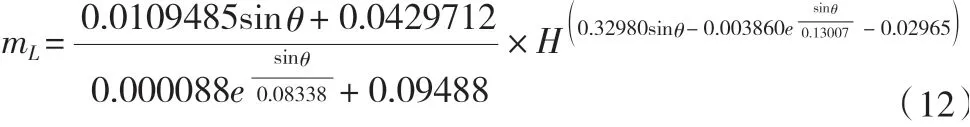
根据式(12)可以得出不同单峰角度下所对应的驼峰堰流量系数取值,具体见表5。

表5 不同单峰角度的驼峰堰流量系数
3.5 流量计算
将式(10)和式(12)代入驼峰堰堰流基本公式后得出如下公式:
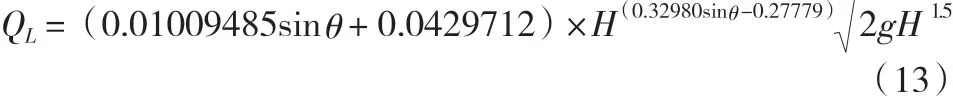
进行驼峰堰过流流量试验值和拟合公式计算值的比较,具体见表6。
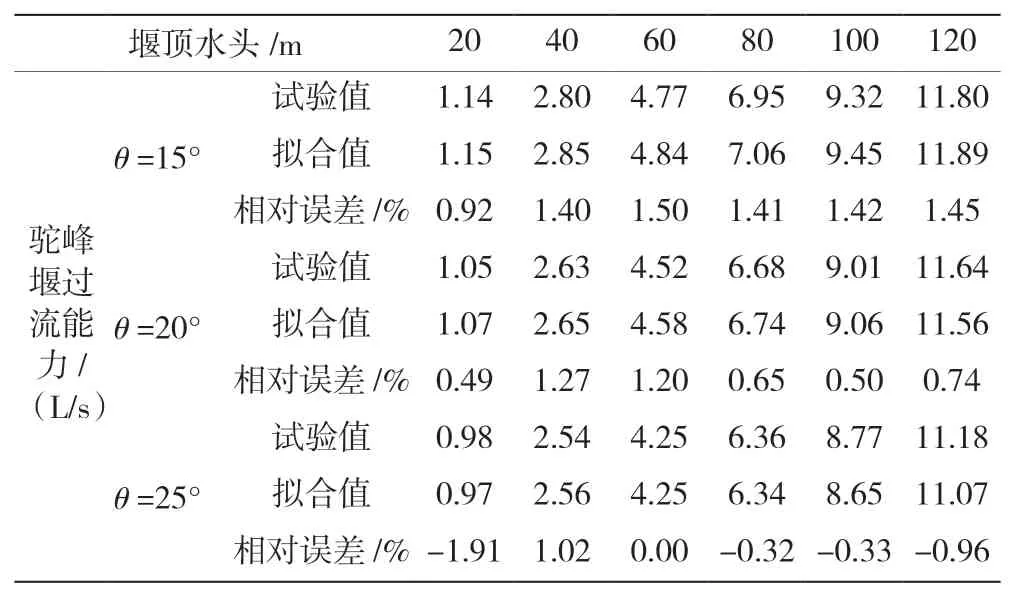
表6 驼峰堰过流流量试验值和拟合值比较
通过对驼峰堰过流流量试验值和拟合值的比较可以看出,当驼峰堰单峰角度=15°时,试验值和拟合值相对误差最大值为1.45%;当驼峰堰单峰角度=20°时,试验值和拟合值相对误差最大值为1.27%;而当驼峰堰单峰角度=25°时,试验值和拟合值相对误差最大值为-1.91%,拟合精度符合工程应用。
4 结论
综上所述,本文依托驼峰堰水工模型试验成果,并以堰流基本公式为基础进行流量系数和驼峰堰堰顶水头的拟合分析,并得出驼峰堰流量拟合公式。基于此得出了可直接用于原型驼峰堰过流能力计算的流量系数公式,且驼峰堰过流流量试验值和拟合值相对误差满足工程应用要求,本文分析结果对水工工程应用具有借鉴指导价值。

