基于数字滤波算法的时域激电场Cole-Cole 模型参数最优化计算

刘瑞泽, 孟庆鑫, 乔圣扬

河北地质大学, 河北 石家庄 050031

0 引言

时间域谱激发极化法是通过测量人工场源引起的大地视时变电阻率特征, 寻找电性异常体, 并根据岩、 矿石时谱参数, 评价电性异常体的一种电法勘探方法[1]。 时谱激电法能获得反映地下不同时间地质信息的电性谱[2], 拥有一定的应用前景[1]。 近年来, 国内外研究者将谱激电法应用于金属矿物分析[3]、 不同流体饱和度岩层[4]、 岩样渗漏率计算[5]、 工程地质勘探中垃圾填埋场污染范围[6]、 监测地球化学场[7]等方面; 同时, 随着科技进步、 仪器设备的改进, 时谱激电法在数据采集[8]、 测量高信噪比[9]等技术方面得到改善, 以及有关时谱激电新的计算方法的引入[10]。 综上所述, 科研人员不仅拓宽时谱激电法的应用领域, 而且完善了理论方法和技术手段, 这些都使时谱激电法得以发展。 上述成果仍需要推广至其他领域, 也需要将其他领域的一些好的理论成果和技术引入到时谱激电法中; 而且, 以往主要研究的是视时变电阻率, 极化率的大小[11]等参数, 在处理一些复杂介质问题时, 这些参数反映出的电性差异不明显, 甚至不能区分电性异常体, 而且解释方法单一[12]。 随着研究的不断深入, 研究者发现谱激电特征参数能够区分复杂介质的电性差异, 这种应用多参数联合解释电性差异的方法日趋普遍[13]。 为了更好的对野外观测数据进行解释, 谱特征参数的最优化计算是有必要的。 故本文将在数字滤波算法的基础上, 完成时谱激电法谱特征参数的最优化计算; 通过理论算例, 验证反算出的谱特征参数的精度; 进行不同充电时间的谱特征参数最优化计算, 分析不同充电时间对谱特征参数精度的影响。

1 时谱激电正演

自激发极化法广泛应用于实际生产后, 研究者在激电谱特性区分矿化类型[14]、 利用在复平面中不同的复电阻率频谱类型定性评价异常源性质[15]、 利用激电衰减时和衰减度等特性找地下水[16]等方面取得重要成果; 此外, 也有研究者在定量描述激电谱特性方面做过许多研究, 其中柯尔-柯尔模型的提出[17][18]提供了对激电谱定量描述的手段。 本文基于柯尔-柯尔模型和数字滤波算法来研究谱特征参数。

1.1 柯尔-柯尔模型

当通过岩、 矿石的供电电流密度不大时, 岩、 矿石的激电效应具有线性规律, 并且在时间范围内可以用不变的参数来描述, 是一个线性不变系统。 Madden和Cantwell、 Pelton 等[17]借 用 了 一 种 与 Cole 和Cole[19]提出的张弛模型类似的传递函数, 来描述复电阻率频谱的性质, 将等效电路模型称之为柯尔-柯尔模型, 函数称之柯尔-柯尔阻抗表达式。

研究者提出的柯尔-柯尔阻抗表达式为[17]:

式中:Z(0)、m、τ、c分别为频率为零时的阻抗、极化率、 时间常数和频率相关系数, 并将其称为柯尔-柯尔参数。Z(0) 的单位为Ω,τ的单位为s,m和c无量纲。

根据上式不难得到在频率域中的复电阻率的柯尔-柯尔表达式[1]:

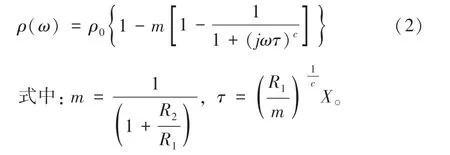
在这一复电阻率的柯尔-柯尔表达式中,ρ0为频率为零时的电阻率, 其余参数与阻抗表达式中的相同,也将这些参数称之为柯尔-柯尔频域谱特征参数。ρ0的单位为Ω,τ的单位为s,m和c无量纲。

1.2 基于数字滤波算法柯尔-柯尔模型的频-时转换

研究者常将柯尔-柯尔模型应用于频域激发极化法中, 并用柯尔-柯尔谱特征参数描述激电谱特性。研究者的研究证实了谱特征参数可以很好的定量描述多数岩、 矿石的激电谱特性, 并指出可以根据岩、 矿石的谱特征参数寻找激电异常体。 本文采用Guptasarma[20]研发的一种计算瞬变响应的数字滤波算法, 对柯尔-柯尔模型进行“频-时” 转换, 以此求取时间域中的电阻率柯尔-柯尔模型。

为了计算复电阻率的柯尔-柯尔表达式ρ(ω) 在t时刻的响应ρ(t) , 首先确定频域复电阻率的虚分量、实分量。 研究者推导出的含有虚分量和实分量的复电阻率表达式为[1,17]:

本数字滤波算法只需要频域复电阻率的实分量,即为:

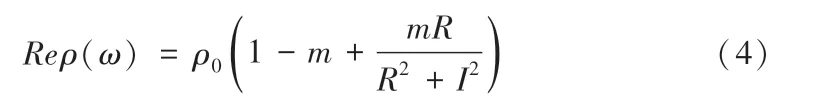
再根据数字滤波的离散式[20]:

Guptasarma 提出的数字滤波算法要用到21 个滤波系数, 然后通过累加的方式来求取电阻率或电位差。

转换成时间域电阻率或电位差的公式后, 要通过建模试算, 观察不同谱特征参数的时间域谱激电法电阻率或电位差特性曲线变化特征[21]。

根据前人的研究文献资料[11,21], 设置多组不同的谱特征参数, 依据不同物质的充电饱和特性和常用观测时道, 以时间作为自变量, 电阻率作为因变量, 来观测不同谱特征参数引起曲线的变化特征。 通过编程的方式, 来绘制不同谱特征参数对应的电阻率和电位差随时间变化的曲线图。

图1 为时间常数和极化率取定值, 时间相关系数在变化的时变电阻率曲线图。 在时间轴为对数比例尺、 时变电阻率为算数比例尺的坐标轴中, 时变电阻率与时间在时间常数取值附近有中心对称的趋势。 并且在远离中心对称点处, 随着频率相关系数数值的增加, 时变电阻率随时间变化的曲线斜率逐渐减小, 而在中心对称点附近, 则随着频率相关系数数值的增加, 时变电阻率随时间变化曲线的斜率增大。

图1 时间常数和极化率取定值, 不同的时间相关系数对应的时变电阻率曲线图Fig.1 The time constant and polarizability are fixed values,and the time-varying resistivity curves corresponding to different time correlation coefficients

图2 为极化率和时间相关系数一定, 时间常数在变化的时变电阻率曲线图。 在时间轴为对数比例尺、时变电阻率为算数比例尺的坐标轴中, 不同时间常数所对应的时变电阻率与时间的关系曲线的变化趋势是一致的, 不同时间常数所对应的时变电阻率随时间的变化曲线可以通过左右平移得到。

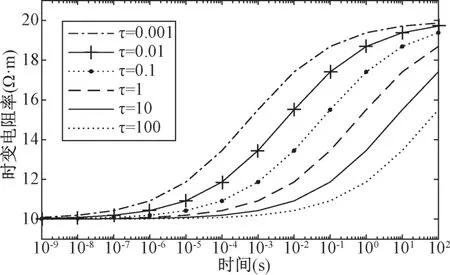
图2 极化率和时间相关系数取定值, 不同的时间常数对应的时变电阻率曲线图Fig.2 The polarizability and time correlation coefficient are taken a fixed value, and the time-varying resistivity curve corresponding to different time constants

图3 为时间常数和时间相关系数一定, 极化率在变化的时变电阻率曲线图。 在时间轴为对数比例尺、时变电阻率为算数比例尺的坐标轴中, 时变电阻率时谱有如下特征: 结果恒为正值, 其数值随时间增大单调地增加; 在长时间供电时, 时变电阻率趋于ρ(∞), 在短时间供电时, 时变电阻率趋于ρ(∞)(1-m) 值。

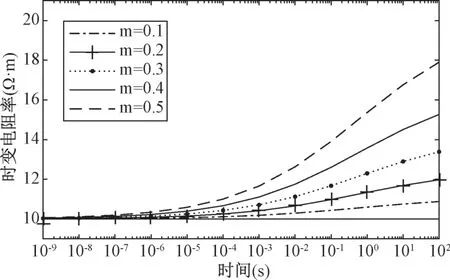
图3 时间常数和极化率取定值, 不同的极化率对应的时变电阻率曲线图Fig.3 The time constant and the polarizability are fixed values, and the time-varying resistivity curves corresponding to different polarizabilities

图4 为不同谱特征参数对应的充放电曲线图。 在横坐标为充电时间, 纵坐标为电位差的充放电曲线中, 不同的谱特征参数对应着不同的充放电曲线。 不同的谱特征参数对应着不同的极化异常现象, 可以通过谱特征参数来区分极化异常。

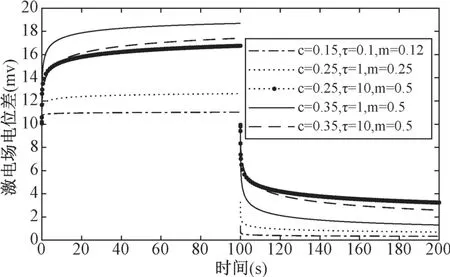
图4 不同谱特征参数对应的充放电曲线图Fig.4 Charge and discharge curves corresponding to different spectral characteristic parameters

2 时间域激电场视谱特征参数最优化计算

根据上文中提到的通过数字滤波算法, 将频域复变电阻率表达式进行“频-时” 转换后, 得到时间域电阻率表达式, 利用编程软件, 完成时谱特征参数最优化计算。 其中, 根据之前的研究[10], 选择常用的理论算例(主要为时间常数和相关系数的选择), 来进行谱特征参数的最优化计算, 并通过理论算例来验证该最优化算法计算的精度。

2.1 目标函数的构建

本文的目标函数采用最小二乘原理来进行构建。首先谱特征参数最优化计算目标函数中的元素(采用了比值的形式, 目的是只对τ,c进行最优化计算, 减少参数, 降低多解性) 为:

式中:mona,moffa分别表示充电和放电时的视充电率, 而视充电率可通过一次场、 二次场电位差的比值获得。

谱特征参数最优化计算的目标函数为:

2.2 视谱特征参数最优化计算的算法步骤

步1: 给出τ1,c1, 0 ≤ε≤1;

k =1。

步2: 如果 ▽φ(τk)2+ ▽φ(ck)2≤ε, 则停;

dk=(-▽φ(τk),-▽φ(ck))。

步3: 如果k=1, 则利用不精确搜索方式求a1,否则,*(dk),k: =k+1, 转步2。

进行视谱特征参数最优解计算时, 首先设置初始时间常数τ1和相关系数值c1, 以及拟合精度, 将初始值和实测数据代入目标函数, 然后根据上述步骤对目标函数迭代求解, 最终满足拟合精度时的时间常数和相关系数就是本文要求的视谱特征参数。 根据上述算法步骤, 进行计算机编程。

步4: (τk+1,ck+1) = (τk,ck) +ak

2.3 理论算例验证

根据之前研究者使用柯尔-柯尔模型进行激发极化法仿真研究时[18][10], 得出了25 组CC 参数模型(c范围从0.1 到0.6,τ范围从0.001 到100 s), 每组谱特征参数模型对应于充电过程中4 个时间点(0.92、0.5、 0.3 和0.2 s) 的测量数据。 依据理论算例, 基于2.1、 2.2 构造的目标函数和算法步骤通过编程软件, 最优化计算出的谱特征参数结果如表1。

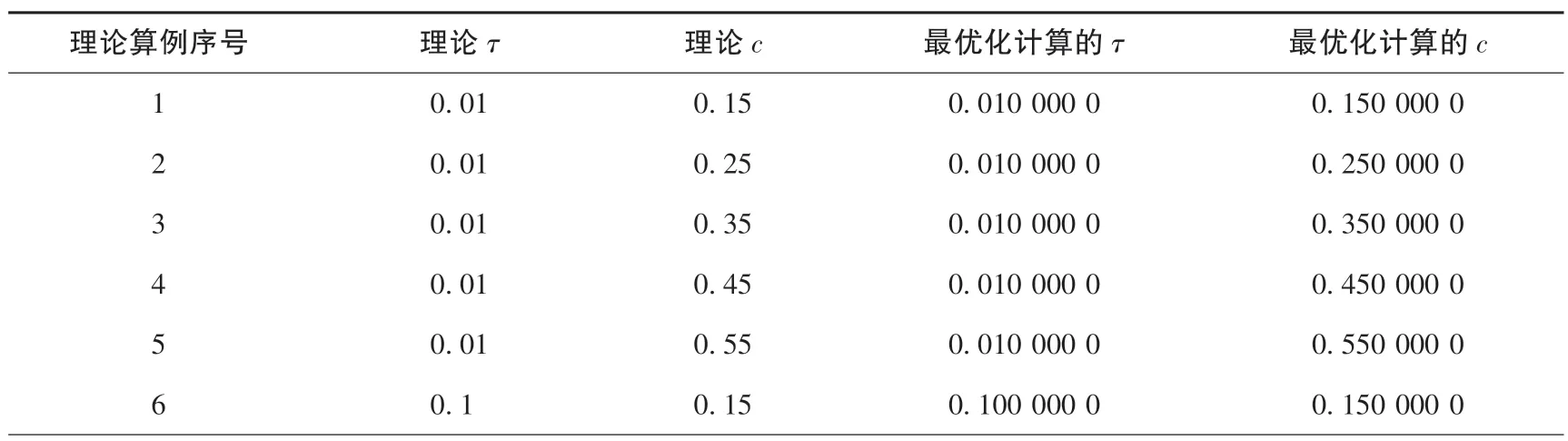
表1 理论算例模型谱特征参数与最优化算法计算出的谱特征参数结果的对比Table 1 Comparison of the spectral characteristic parameters of the theoretical calculation example model and the results of the spectral characteristic parameters calculated by the optimization algorithm

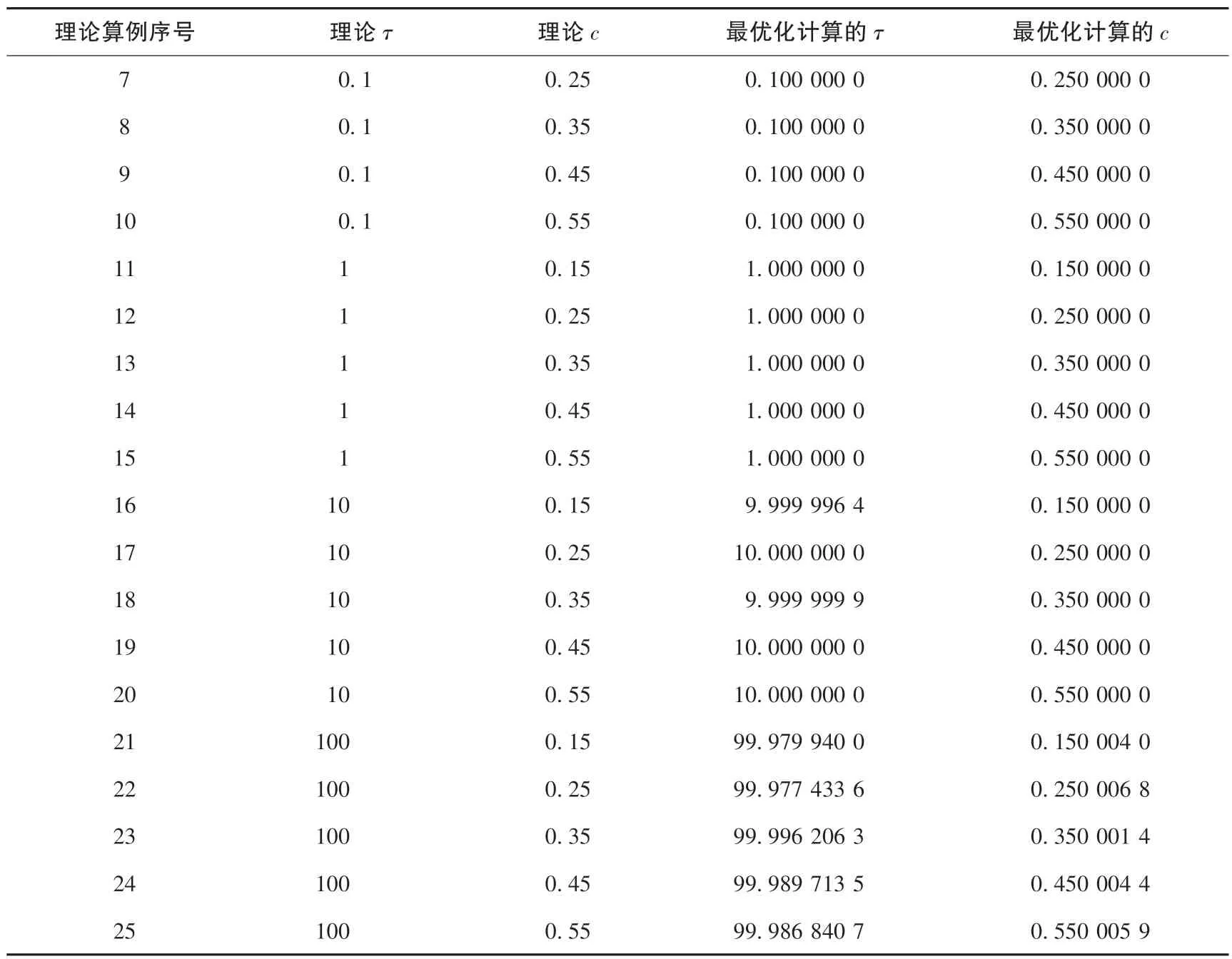
续表1

表1 的左侧为具体谱特征参数(τ、c) 试算模型数值, 表1 的右侧是25 组理论算例模型的谱特征参数最优化计算结果。 从视谱特征参数最优化算法计算出的谱特征参数τ、c的结果来看, 反算的谱特征参数于所设的理论算例高度一致。 通过计算反算谱特征参数与理论的谱特征参数的相对误差发现, 它们的相对误差都小于1‰。 这说明谱特征参数的最优化计算结果与理论值有很高的拟合精度, 该算法对理论算例来说是可行的。

3 结论

(1) 基于数字滤波算法对柯尔-柯尔模型进行频时变换得到了时域表达式, 根据该表达式绘制了不同时刻和谱特征参数条件的时谱曲线, 分析可知, 不同谱特征参数对应的时谱曲线有明显的不同, 可以根据谱特征参数所反应的时变特性来区分极化异常体。

(2) 本文构建了比值形式的目标函数, 该目标函数需要反算的视谱特征参数少, 在当前主流仪器观测时道较少的情况下, 具有降低反算结果的多解性。

(3) 通过理论算例试算, 证明本文编写的视谱特征参数最优化算法是可行的, 而且反算的结果精确度较高。

(4) 本文只验证了试理论算例的谱特征参数, 之后的研究, 要将该方法应用于简单地质模型进行验证,最终目的是将该方法应用于野外实测数据的处理, 以计算的谱特征参数来寻找异常区域。 同时也发现, 数字滤波算法转换后的柯尔-柯尔模型计算量比较大, 接下来的研究将降低此算法的计算量大的问题。