基于水面蒸发量及气温因子的潜水蒸发量计算模型研究
王怡宁,丁佳楠,吕海深,宋翠萍,周超,刘竹梅,陆云燕
▪水土资源与环境▪
基于水面蒸发量及气温因子的潜水蒸发量计算模型研究
王怡宁1, 2,丁佳楠2*,吕海深2,宋翠萍3,周超4,刘竹梅2,陆云燕2
(1.南京水利科学研究院,南京 210029;2.河海大学,南京 211100;3.江苏省水利勘测设计研究院有限公司,南京 210000;4.安徽省(水利部淮委)水利科学研究院 五道沟实验站,安徽 蚌埠 233000)
【】探究不同气象因子对潜水蒸发量的影响。利用五道沟水文试验站0.3 m2口径的蒸渗仪测定潜水蒸发量,以及气象观测场的相关仪器测定气象数据,选取2006—2015年潜水蒸发量和气象实测数据,分别构建了砂姜黑土和黄潮土基于埋深因子的裸地潜水蒸发量与水面蒸发量、气温单气象因子和双气象因子计算模型。砂姜黑土各计算模型2在0.88左右,平均绝对误差()为1.50 mm/10 d,均方根误差()为2.30 mm/10 d;黄潮土各计算模型2为0.92,平均绝对误差()为1.94 mm/10 d,均方根误差()为2.80 mm/10 d,均有较高的精度,且黄潮土各拟合模型的精度要高于砂姜黑土。单气象因子计算模型的2为0.92,平均绝对误差()为1.80 mm/10 d,均方根误差()为2.60 mm/10 d;双气象因子计算模型的2为0.94,平均绝对误差()为1.40 mm/10 d,均方根误差()为2.05 mm/10 d,双气象因子拟合效果高于单气象因子。2种土壤多气象因子复合模型,其平均绝对误差()分别为2.21 mm/10 d和2.91 mm/10 d,均方根误差()分别为3.31 mm/10d和3.93 mm/10 d,估算精度较优。潜水埋深、水面蒸发量及气温对潜水蒸发量具有显著影响,可根据各地区获得的气象资料选择合适的计算模型。
潜水蒸发量;水面蒸发量;气温;埋深
0 引言
【研究意义】潜水蒸发是指潜水在土壤吸力的作用下,向包气带土壤中输送水分,并通过土壤蒸发和植物蒸腾而进入大气的过程。多年来许多学者对潜水蒸发的规律做了大量的研究,均认为影响潜水蒸发的2个主要因素为:土壤输水能力[1-2]和大气蒸发能力[3-4],土壤输水能力的大小主要取决于潜水埋深、土壤质地以及土壤含水量等,而大气蒸发能力的大小主要取决于地表温度、平均气温、水面蒸发量等气象要素,二者相互影响,相互作用。对潜水蒸发规律的探讨有助于研究地下水浅埋区农作物耗水机制、灌溉制度、地下水位调控以及土壤次生盐碱化等问题[5-8]。
【研究进展】目前国内外学者对潜水蒸发计算模型做了大量的研究探讨,主要体现在二方面:一是利用经验法建立潜水蒸发计算模型,例如现有的经验公式阿维里扬诺夫公式[1]、清华大学公式[1]张朝新公式[9]、叶水庭公式[9]等均是采用经验法;二是利用理论法建立潜水蒸发的机理模型。束龙仓等[1]对阿维里扬诺夫和叶水庭公式进行比较,并提出改进形式,结果表明改进后的公式拟合精度较原有公式有所提高;唐海行等[9]对已有的经验公式进行改进,引入土壤水分运动参数概念,并对改进后的公式进行验证;张永明等[10]采用中国科学院阿克苏水平衡试验站1990—1996年数据,通过分析裸地潜水蒸发计算模型的控制条件,建立了新的计算模型,结果表明所建立的模型符合控制条件;刘路广等[11]在叶水庭公式的基础上加入了降雨量因子,建立了以水面蒸发、降雨量以及潜水埋深为因变量,潜水蒸发量为自变量的计算模型;许莹莹等[12]利用主成分分析从多个气象因子中提取主要因子作为解释变量,与潜水蒸发量建立多元回归模型,结果表明众多气象因子可以分为3个主成分,与其建立的多元回归模型精度较高,可用于潜水蒸发量的计算;刘诚明等[13]采用与太阳辐射密切相关的气温、地温等气象因子与潜水蒸发量的相关系数建立对数模型,结果表明利用与太阳辐射有关的气象因子推算潜水蒸发量可行。【切入点】目前众多学者对潜水蒸发的计算模型做了大量的研究,目前的经验公式大多涉及水面蒸发这一气象因子,对其他气象因子涉及不多。【拟解决的关键问题】为了能更精确地计算潜水蒸发量,可尝试同时用多个不同的气象因子进行组合模拟估算。本文采用五道沟地区2006—2015年的潜水蒸发量以及气象要素实测资料,采用水面蒸发和气温2种气象因子分别对基于埋深与潜水蒸发关系的影响进行分析研究,并构建潜水蒸发计算模型。
1 试验与方法
1.1 试验区概况
五道沟水文实验站是淮河平原综合性实验站,位于淮北平原的南部,蚌埠市北25 km处新马桥原种场境内,占地面积1.4万m2。淮北平原位于我国的南北过渡地带,是我国重要的粮棉油产区,也是水资源开发利用程度高的缺水地区。淮北平原四季分明,属暖温带半湿润季风气候区,多年平均降水量800 mm左右,主要集中在6—8月,易旱易涝,地下水位埋深为1~5 m,南部区地下水年变幅为1~3 m,属于地下水浅埋区,水交换频繁。实验站内配有大型地中蒸渗观测室以及气象观测场等设施,实验区内代表土壤为砂姜黑土和黄潮土,积累了60余年不间断的长系列水文实验资料。
1.2 试验方案
本文选取五道沟实验站2006—2015年砂姜黑土裸地0.2、0.4、0.6、0.8、1.0、2.0、3.0、5.0 m控制潜水埋深和黄潮土裸地0.2、0.4、0.6、1.0、2.0、3.0、4.0 m控制潜水埋深0.3 m2口径蒸渗仪潜水蒸发量,采用水面蒸发及气温2个气象因子的实测资料,分别对潜水蒸发与水面蒸发量和气温进行分析,并依次建立计算模型,最后将所得的各计算模型进行组合调试,得到以水面蒸发量、气温以及埋深为因变量,潜水蒸发量为自变量的多元综合模型,通过计算平均绝对误差()以及均方根误差()来判断模型的精度是否满足要求。
1.3 模型评价指标
本文采用决定系数(2)、平均绝对误差()以及均方根误差()3个统计指标对模型精度进行评价,各统计指标的计算式见式(1)—式(4)。
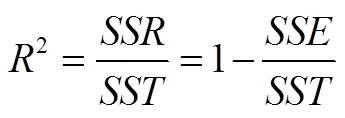
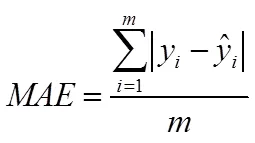
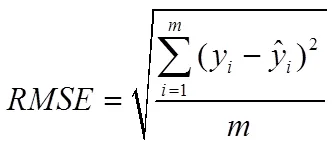
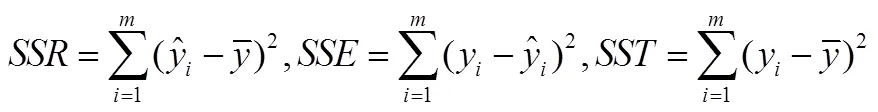
式中:y为潜水蒸发量实测值;为潜水蒸发量计算值;为样本数,=1,2,…,为样本序数;为回归平方和;为残差平方和;为总平方和。2越大,说明自变量对因变量的解释程度越高,即模型的精度越好,平均绝对误差()和均方根误差()的值越小说明模型精度越高。
2 结果与分析
2.1 潜水蒸发量与水面蒸发量的关系模拟
2.1.1 水面蒸发量与潜水蒸发量关系分析
利用2006—2015年数据,分析裸地砂姜黑土和黄潮土0.2、0.4、0.6 m不同埋深处的10 a平均旬潜水蒸发量与旬水面蒸发量的变化关系,二者关系如图1所示。由图1可知,砂姜黑土和黄潮土裸地情况下潜水蒸发量与水面蒸发量均呈幂函数关系,根据判定系数2可知,二者关系显著,这与相关研究[14-16]结果一致。说明潜水蒸发量均随着水面蒸发量的增大而增大,当水面蒸发量增大到一定程度时,潜水蒸发量趋于某一极限值。这是因为潜水蒸发量同时受大气蒸发能力和土壤输水能力的共同影响,当大气蒸发能力小于土壤输水能力时,潜水蒸发量主要受大气蒸发能力的影响,随水面蒸发量的增大而增大;当土壤输水能力小于大气蒸发能力时,此时潜水蒸发量主要受土壤输水能力限制,缓慢增加并趋于极限值。

图1 不同土质潜水蒸发量与水面蒸发量关系图
由图1可知,相同埋深不同土质条件下,潜水蒸发量与水面蒸发量呈现出的关系存在差别,水面蒸发量对黄潮土的影响大于砂姜黑土,这是因为砂姜黑土较黄潮土的黏性更强,土壤空隙更小,透水性差,不利于水分的传输迁移。
2.1.2 模型拟合
根据2006—2015年裸地砂姜黑土和黄潮土2种土质的10 a平均潜水蒸发量以及水面蒸发量,建立以潜水埋深及水面蒸发量为自变量,潜水蒸发量为因变量的计算模型,通过调试得到如式(5)—式(6)的具体计算模型:
砂姜黑土:
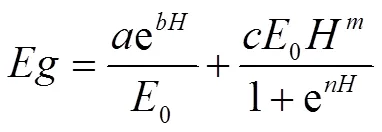
黄潮土:
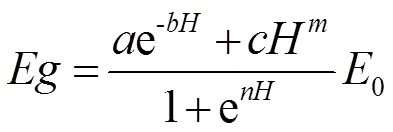
式中:为潜水蒸发量(mm);0为水面蒸发量(mm);为潜水埋深(m);、、、、均为拟合参数。
利用Matlab编程软件,采用2006—2015年的10 a平均潜水蒸发量和水面蒸发量进行拟合,得出各参数值,进而得到具体的计算模型,如式(7)—式(8)。
砂姜黑土:

黄潮土:
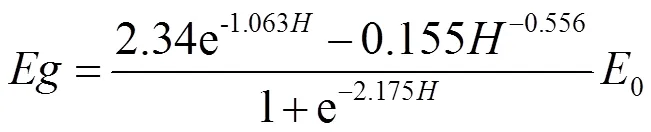
式(7)各统计指标的值分别为:2=0.898,=1.368 mm/10 d,=2.203 mm/10 d,决定系数2>0.7,平均绝对误差()和均方根误差()均在3 mm/10 d以内,说明模型拟合效果较好(0<≤5 m);式(8)的统计指标值分别为:2=0.958,=1.935 mm/10 d,=2.338 mm/10 d,说明模型的拟合效果较好,可用于潜水蒸发量的计算(0<≤4 m)。
2.2 潜水蒸发量与气温的关系及模型拟合
2.2.1 潜水蒸发量与气温关系分析
采用2006—2015年数据,绘制裸地砂姜黑土和黄潮土不同埋深处10 a平均旬潜水蒸发量与气温随时间变化过程线如图2。由图2可见,10 a平均潜水蒸发量的变化趋势与气温呈较高的一致性,这与相关研究中[17],潜水蒸发量与气温呈较强的正相关关系的结果一致。气温一般在7、8月最高,而此时的潜水蒸发量却呈现出下降的趋势,这是因为7、8月为淮北平原的汛期,降雨较其他月频繁,此时潜水蒸发量的大小受降雨的影响较为显著。由图2(a)可知,气温对砂姜黑土潜水埋深0.4 m以内影响较大;而由图2(b)可知,气温对黄潮土潜水埋深1.0 m以内影响较大。这是因为砂姜黑土黏粒量占13.1%,粉粒量占49.4%,砂粒量占37.5%,黄潮土中黏粒量占2.0%,粉粒量占11.5%,砂粒量占37.5%。砂姜黑土的黏粒和粉粒量高于黄潮土,说明砂姜黑土较黄潮土黏性更大,空隙更小,阻水能力更强,不利于水分的迁移,而黄潮土土壤黏性小空隙大,有利于水分的输送,透水性要强于砂姜黑土。
2.2.2 模型拟合
根据2006—2015年10 a平均裸地潜水蒸发量及气温数据拟合模型,建立以潜水埋深及气温为自变量,潜水蒸发量为因变量的计算模型,具体模型形见式(9)—式(10)。
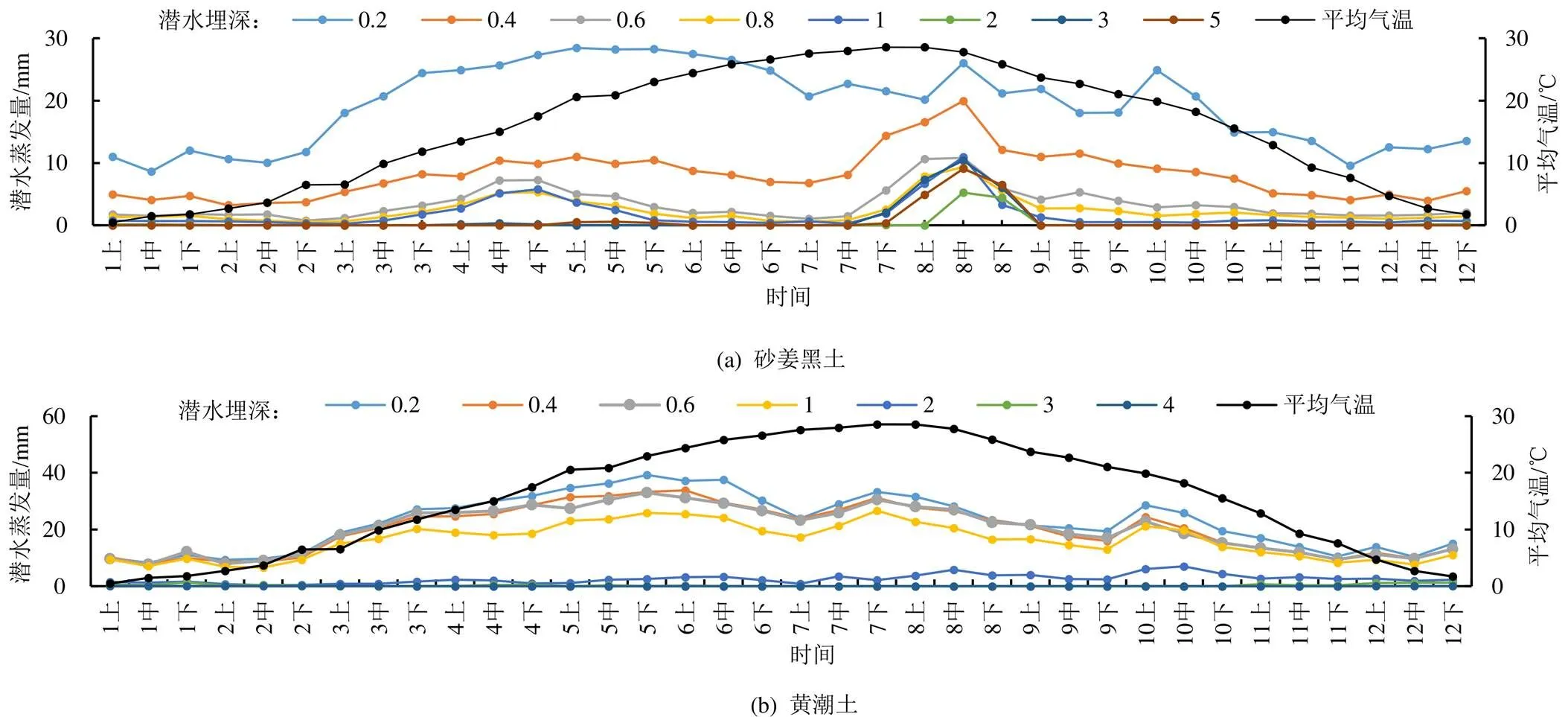
图2 不同土质潜水蒸发量与气温变化趋势图
砂姜黑土:
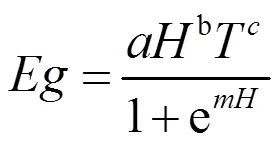
黄潮土:

式中:为气温(℃);其他符号意义同前。
采用2006—2015年多年10 a平均裸地潜水蒸发量和气温,利用Matlab编程软件进行模型拟合,得出各参数值,进而得到具体的计算模型,如式(11)—式(12)。
砂姜黑土:
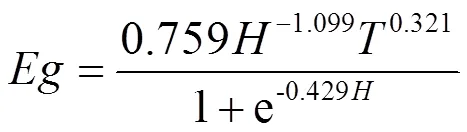
黄潮土:

式(11)中检验其精度的各统计指标值分别为:2=0.860,=1.634 mm/10 d,=2.556 mm/10 d,决定系数2>0.7,且平均绝对误差()和均方根误差()均小于4 mm/10 d,则说明该拟合模型的精度符合要求(0<≤5 m);式(12)中检验精度的各统计指标值分别为:2=0.903,=2.416 mm/10 d,=3.505 mm/10 d,符合模型的精度要求。说明上述模型均能用于潜水蒸发量的计算(0<≤4 m)。
2.3 潜水蒸发量与水面蒸发量及气温双气象因子模型
2.3.1 模型拟合
上文分别分析了水面蒸发量及气温单个气象因子对不同土质下裸地潜水蒸发的影响,并分别求得了相应的潜水蒸发量计算模型式(7)、式(8)和式(11)、式(12)。为使求得的计算模型更加准确以及更加接近于实际,可利用水面蒸发量及气温2个气象因子综合求解潜水蒸发量,即分别将式(5)和式(9)相加,将式(6)和式(10)相加,得到如式(13)—式(14)的计算模型:
砂姜黑土:
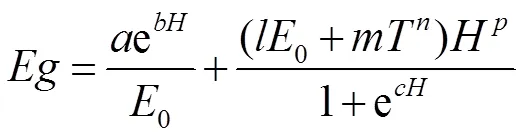
黄潮土:

式中:、、、、、、、均为拟合参数;其他符号意义同前。
利用2006—2015年五道沟实验站长期实测资料对上述公式进行拟合,得到各拟合参数的具体数值,从而得到具体的潜水蒸发量的计算模型,具体模型见式(15)—式(16)。
砂姜黑土:
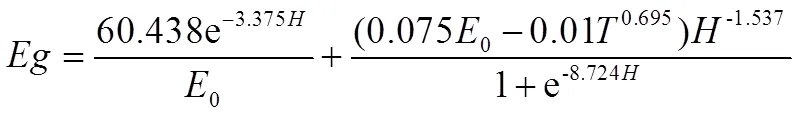
黄潮土:

式(15)中各模型评价指标的值分别为:2=0.898,=1.340 mm/10 d,=2.180 mm/10 d,决定系数2>0.7,且平均绝对误差()和均方根误差()均在4 mm/10 d以内,说明该计算模型达到精度要求(0<≤5 m);式(16)中判断模型精度的各统计指标值分别为2=0.968,=1.484 mm/10 d,=2.025 mm/10 d,满足精度要求(0<≤4 m),可用于不同土质潜水蒸发量的计算。
由上述分析可知,以水面蒸发量和气温2个气象因子为研究对象的模型精度要比以单个气象因子作为研究对象的模型精度高,说明以双气象因子作为自变量的计算模型的可信度高于单气象因子的计算模型。
2.3.2 模型评价
采用五道沟水文实验站2018—2019年裸地潜水蒸发量及气象数据对上述模型进行检验,潜水埋深较浅时,潜水蒸发量较明显,因此以0.2 m埋深为例,绘制砂姜黑土和黄潮土在此埋深处的旬潜水蒸发量实测值与估算值对比图,见图3。
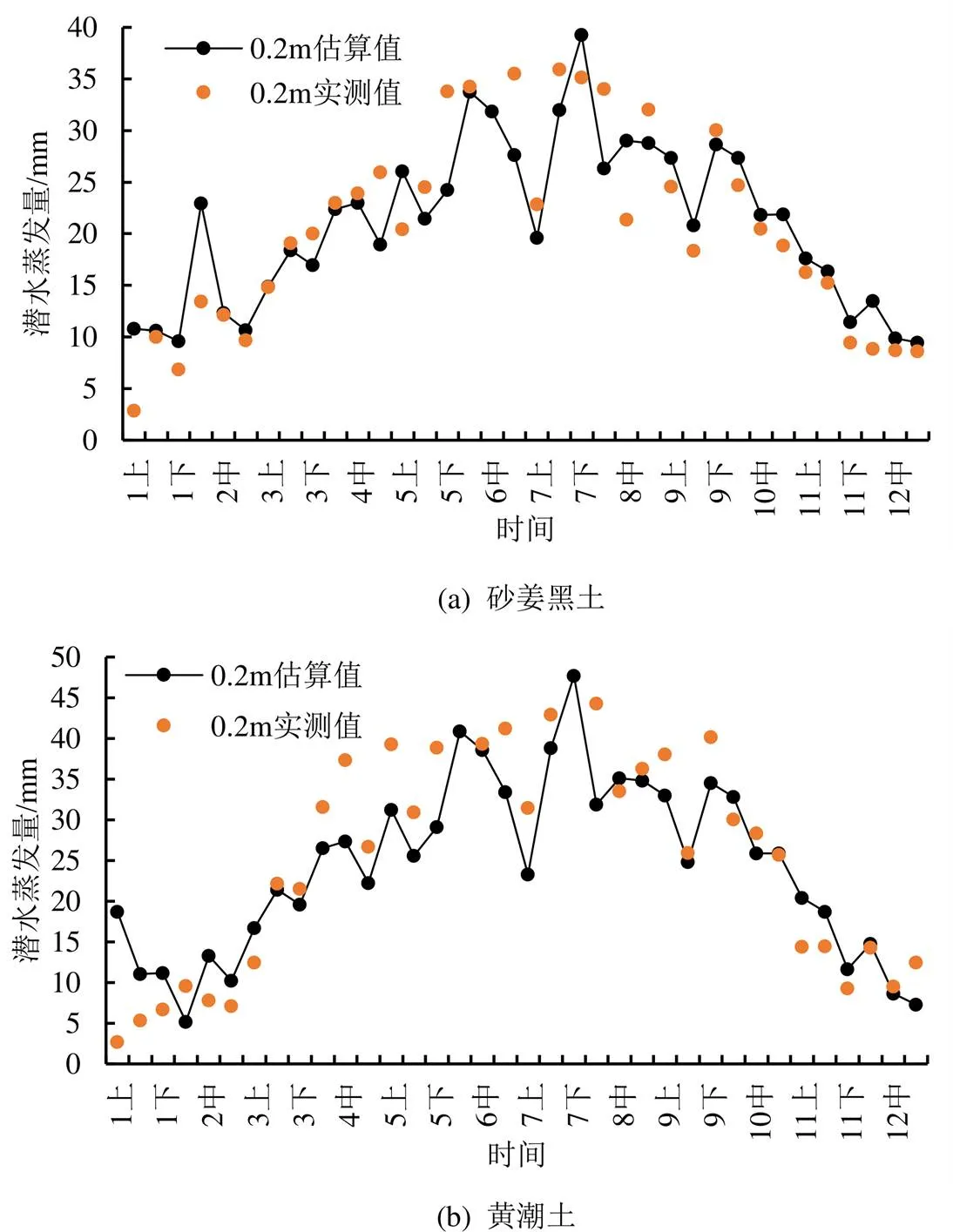
图3 不同土质0.2 m埋深潜水蒸发量估算值和实测值对比
裸地砂姜黑土和黄潮土不同埋深处的各评价指标值见表1、表2。由表1、表2可知,砂姜黑土和黄潮土各埋深的平均绝对误差()和均方根误差()均小于4,说明上述2种土壤拟合模型的估算效果均优。
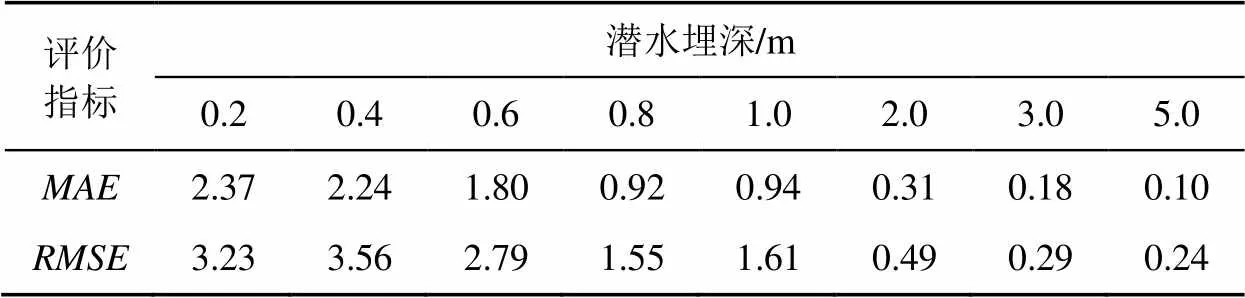
表1 砂姜黑土评价指标值
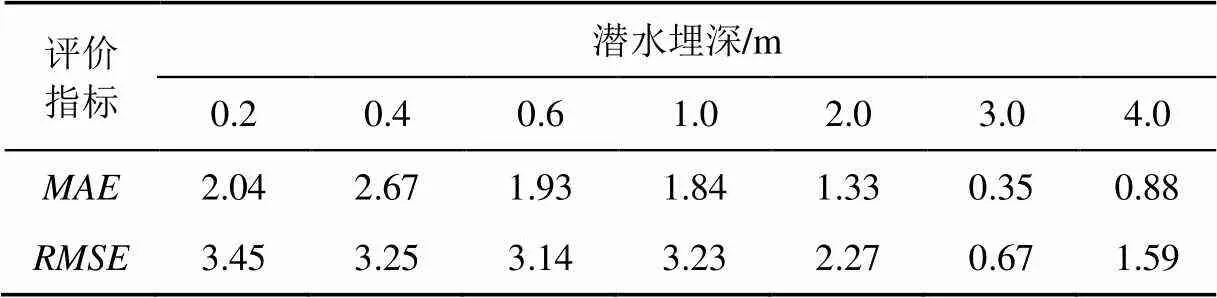
表2 黄潮土评价指标值
为进一步证明上述模型的精度是否达到要求,利用2018—2019年数据对式(15)和式(16)进行整体评价,得到式(15)的评价指标值为:平均绝对误差()=2.212 mm/10 d,均方根误差()=3.306 mm/10 d;式(16)的评价指标值为:平均绝对误差()=2.908 mm/10 d,均方根误差()=3.926 mm/10 d。均满足精度要求,式(15)和式(16)可用于裸地潜水蒸发量的计算。
3 讨论
本文以五道沟水文实验站为研究区域,探究不同气象因子对裸地潜水蒸发量的影响,旨在证明裸地潜水蒸发量与气象要素密切相关,这与许莹莹等[12]、刘诚明等[13]的研究结果一致。
以水面蒸发和平均气温为例,分析水面蒸发量和气温对不同土质裸地潜水蒸发量的影响,并分别建立相关计算模型,结果表明,黄潮土各计算模型精度高于砂姜黑土,双气象因子计算模型精度高于单气象因子模型的精度,拟合模型均能用于潜水蒸发量的计算。本文的创新点在于拟合了潜水蒸发量与水面蒸发量、潜水蒸发量与气温的单气象因子模型以及潜水蒸发量与水面蒸发量、气温的双气象因子模型,这与刘路广等[11]的研究存在差异,其在叶水庭公式的基础上加入了降雨量因子,建立了以水面蒸发量、降雨量及潜水埋深为自变量,潜水蒸发量为因变量的计算模型。
本文主要选取了水面蒸发量和气温2个气象因子进行研究,其他气象因子对不同土质裸地潜水蒸发量的研究还有待进一步研究。
4 结论
1)砂姜黑土和黄潮土裸地情况下潜水蒸发量与水面蒸发量均呈幂函数关系,且函数关系显著。分别建立了以水面蒸发量和潜水埋深为自变量,潜水蒸发量为因变量的裸地砂姜黑土和裸地黄潮土的计算模型,模型评价指标2、、均达到精度要求,模型拟合效果较好。
2)裸地情况下,潜水蒸发量的变化趋势与气温呈较高的一致性,对二者进行模型拟合,得到砂姜黑土和黄潮土2种土质裸地情况下的潜水蒸发量计算模型,模型评价指标2、、均达到精度要求,模型拟合效果较好。
3)双气象因子拟合的模型精度要高于单气象因子拟合的模型精度,单气象因子所拟合的模型也能用于计算潜水蒸发量,采用双气象因子的复合模型可提高计算精度。
[1] 束龙仓, 荆艳东, 黄修东, 等. 改进的无作物潜水蒸发经验公式[J]. 吉林大学学报(地球科学版), 2012, 42(6): 1 859-1 865.
SHU Longcang, JING Yandong, HUANG Xiudong, et al. On the development of improved empirical formulas for calculating the phreatic water evaporation for bare land[J]. Journal of Jilin University (Earth Science Edition), 2012, 42(6): 1 859-1 865.
[2] 贾瑞亮, 周金龙, 高业新, 等. 干旱区高盐度潜水蒸发规律初步分析[J]. 水科学进展, 2015, 26(1): 44-50.
JIA Ruiliang, ZHOU Jinlong, GAO Yexin, et al. Preliminary analysis on evaporation rules of high-salinity phreatic water in arid area[J]. Advances in Water Science, 2015, 26(1): 44-50.
[3] 王思如, 雷慧闽, 段利民, 等. 气候变化对科尔沁沙地蒸散发和植被的影响[J]. 水利学报, 2017, 48(5): 535-544, 550.
WANG Siru, LEI Huimin, DUAN Limin, et al. Simulated impacts of climate change on evapotranspiration and vegetation in Horqin Sandy Land[J]. Journal of Hydraulic Engineering, 2017, 48(5): 535-544, 550.
[4] 王振龙, 刘淼, 李瑞. 淮北平原有无作物生长条件下潜水蒸发规律试验[J]. 农业工程学报, 2009, 25(6): 26-32.
WANG Zhenlong, LIU Miao, LI Rui. Experiment on phreatic evaporation of bare soil and soil with crop in Huaibei plain[J]. Transactions of the Chinese Society of Agricultural Engineering, 2009, 25(6): 26-32.
[5] 贾云茂. 裸地条件下农田潜水蒸发规律及其计算[J]. 山西科技, 2008, 23(6): 116-118.
JIA Yunmao. Rules and calculation of the groundwater evaporation in bare farmland[J]. Shanxi Science and Technology, 2008, 23(6): 116-118.
[6] 周超, 王振龙. 砂姜黑土区有无作物生长潜水蒸发规律模拟实验[J]. 安徽农学通报, 2018, 24(24): 81-83.
ZHOU Chao, WANG Zhenlong. Simulation experiment on phreatic water evaporation law with or without crop growth in Shajiang black soil area[J]. Anhui Agricultural Science Bulletin, 2018, 24(24): 81-83.
[7] 尚松浩, 毛晓敏. 潜水蒸发研究进展[J]. 水利水电科技进展, 2010, 30(4): 85-89, 94.
SHANG Songhao, MAO Xiaomin. Research progress on evaporation from phreatic water[J]. Advances in Science and Technology of Water Resources, 2010, 30(4): 85-89, 94.
[8] 张振华, 史文娟, 褚桂红. 干旱区潜水蒸发的影响因素和计算方法分析[J]. 水资源与水工程学报, 2008, 19(6): 78-80.
ZHANG Zhenhua, SHI Wenjuan, CHU Guihong. Influence factor and calculation method of phreatic evaporation in arid region[J]. Journal of Water Resources and Water Engineering, 2008, 19(6): 78-80.
[9] 唐海行, 苏逸深, 张和平. 潜水蒸发的实验研究及其经验公式的改进[J]. 水利学报, 1989, 20(10): 37-44, 72.
[10] 张永明, 胡顺军, 翟禄新, 等. 塔里木盆地裸地潜水蒸发计算模型[J]. 农业工程学报, 2009, 25(1): 27-32.
ZHANG Yongming, HU Shunjun, ZHAI Luxin, et al. Models for calculating phreatic evaporation from bare soil in Tarim Basin[J]. Transactions of the Chinese Society of Agricultural Engineering, 2009, 25(1): 27-32.
[11] 刘路广, 崔远来, 冯跃华. 引黄灌区潜水蒸发规律与计算方法研究[J].灌溉排水学报, 2011, 30(3): 18-22, 33.
LIU Luguang, CUI Yuanlai, FENG Yuehua. Change law and calculation method of phreatic evaporation in the Yellow River irrigation district[J]. Journal of Irrigation and Drainage, 2011, 30(3): 18-22, 33.
[12] 许莹莹, 李薇, 王振龙, 等. 基于主成分分析的裸地潜水蒸发与气象要素关系模拟[J]. 水文, 2020, 40(4): 7-13, 39.
XU Yingying, LI Wei, WANG Zhenlong, et al. Simulation of relationship between evaporation and meteorological elements of bare ground diving based on principal component analysis[J]. Journal of China Hydrology, 2020, 40(4): 7-13, 39.
[13] 刘诚明, 戚莓, 邱胜彬. 用气象因子推算潜水蒸发[C]//新疆水利学会获奖论文集(1989—1998). 1999: 211-219.
[14] 于海龙, 姜峰, 苏浩. 气象因素对潜水蒸发影响探讨[J]. 水土保持应用技术, 2011(3): 24-25.
YU Hailong, JIANG Feng, SU Hao. Discussion on the influence of meteorological factors on diving evaporation [J]. Technology of Soil and Water Conservation, 2011(3): 24-25.
[15] 武金慧, 李占斌. 水面蒸发研究进展与展望[J]. 水利与建筑工程学报, 2007, 5(3): 46-50.
WU Jinhui, LI Zhanbin. Advances and prospect of research on water surface evaporation[J]. Journal of Water Resources and Architectural Engineering, 2007, 5(3): 46-50.
[16] 苏浩, 单丽. 辽宁中部平原区潜水蒸发影响因素及变化规律[J]. 东北水利水电, 2007, 25(9): 32-34, 72.
SU Hao, SHAN Li. Influence factor of phreatic water and variation law in centre plain of Liaoning Province[J]. Water Resources & Hydropower of Northeast China, 2007, 25(9): 32-34, 72.
[17] 陆小明, 杨秒, 王振龙, 等. 淮北平原气象因素对裸地潜水蒸发的影响[J]. 灌溉排水学报, 2019, 38(4): 84-91.
LU Xiaoming, YANG Miao, WANG Zhenlong, et al. Metrological factors affecting evaporation of shallow groundwater in the absence of plants in Huaibei plain[J]. Journal of Irrigation and Drainage, 2019, 38(4): 84-91.
Estimating Shallow Groundwater Evaporation Based on Surface Evaporation and Ambient Air Temperature
WANG Yining1,2, DING Jia’nan2*, LYU Haishen2, SONG Cuiping3, ZHOU Chao4, LIU Zhumei2, LU Yunyan2
(1.Nanjing Institute of Water Resources, Nanjing 210029, China; 2.Hohai University, Nanjing 210098, China;3.Jiangsu Water Conservancy Survey and Design Research Institute Co., Ltd., Nanjing 210000, China; 4.Anhui Province (Huaiwei Committee of the Ministry of Water Resources) Wudaogou Experimental Station of Water Conservancy Research Institute, Bengbu 233000, China)
【】Evaporation loss via capillary rise is an important component of groundwater cycle but difficult to measure in situ. This paper presents an empirical formula to estimate it using surface evaporation and ambient air temperature, based on long-term experimental data obtained from a hydrological experimental station.【】Groundwater evaporation from phreatic surface of shallow groundwater was measured from lysimeters with cross section of 0.3 m2at Wudaogou Hydrological Experiment Station, and the meteorological data were measured from a weather station installed at the station. There were two soils, a fluvo-aquic soil and a lime concretion black soil. For each soil, we established a regression model using temperature and surface evaporation, either separately or in combination, to estimate groundwater evaporation. 【】For the lime concretion black soil, the average2of the models using single or two meteorological factors was 0.88, and its associated average absolute error () and root mean square error () were 0.15 mm/d and 0.23 mm/d, respectively. For the yellow fluvo-aquic soil, the associated results were2=0.92,=0.194 mm, and=0.28 mm/d. When using a single meteorological factor, the average2for the two soils using all models was2=0.92, and its associatedandwere 0.18 mm/d and 0.26 mm/d, respectively. In contrast, in using the two meteorological factors, the average2for the two soils using all models was 0.94, and its associatedandwere 0.14 mm/d and 0.205 mm/d, respectively. 【】For a given area, the evaporation of its shallow groundwater via capillary rise depends on surface evaporation and ambient air temperature. Since air temperature and surface evaporation are closely correlated, we can use either one of the two factor or their combination to estimate the groundwater evaporation.
shallow groundwater evaporation; surface water evaporation; air temperature; groundwater depth
王怡宁, 丁佳楠, 吕海深, 等. 基于水面蒸发量及气温因子的潜水蒸发量计算模型研究[J]. 灌溉排水学报, 2022, 41(3): 69-74.
WANG Yining, DING Jia’nan, LYU Haishen, et al. Estimating Shallow Groundwater Evaporation Based on Surface Evaporation and Ambient Air Temperature[J]. Journal of Irrigation and Drainage, 2022, 41(3): 69-74.
2021-03-25
国家青年基金项目(52109029);国家自然科学基金项目(41571015);国家重点研发计划项目(2017yFC0404504)
王怡宁(1992-),女。工程师,博士研究生,主要从事水文水资源研究。E-mail: wyn6563@163.com
丁佳楠(1997-),江苏泰州人。硕士研究生,主要从事水文水资源统计与分析。E-mail: 2461112179@qq.com
A
10.13522/j.cnki.ggps.2021105
1672 - 3317(2022)03 - 0069 - 06
责任编辑:赵宇龙

