黄土地区拱形骨架边坡防护机理及结构优化

张洪杰

（中国铁路兰州局集团有限公司 兰州工程建设指挥部，甘肃 兰州 730031）

0 引言

在黄土地区的铁路建设中，常因降雨导致自身结构稳定出现问题，其原因主要为雨水入渗造成边坡土体含水量增加，土体强度和基质吸力降低，造成安全系数显著降低。因此，在边坡修建时应采用骨架防护，以保证其自身结构的整体性和稳定性［1-3］。骨架防护是通过混凝土或浆砌片石对边坡进行人工加固而形成的框架式构筑物，可防止边坡滑塌溜坍，常见骨架防护结构型式主要为矩形和拱形［4-5］。相对于其他结构，拱形骨架具有跨度大、节省材料、承载能力强等优点，对于结构尺寸的优化具有重要作用［6-7］。研究拱形骨架在边坡防护中的影响并进行结构优化具有重要意义。

近年来，骨架防护对于边坡的影响效应越来越受到关注，但在骨架结构优化方面的理论研究较少。原泽等［8］通过试验模拟降雨对裸坡和骨架防护边坡的冲蚀作用，提出骨架边坡防护对于坡面径流、土体冲蚀等有明显降低作用，但骨架尖角或边缘部位受雨水冲蚀作用明显，影响边坡稳定性；连继峰等［9-10］结合Mohr-Coulomb 理论，提出在降雨条件下无限长土质斜坡的顺坡破坏模式，该模式可更好地进行土坡浅层稳定分析；连继峰等［11-12］还通过无限长斜坡浅层稳定分析，提出矩形骨架防护效应，并进行了骨架结构优化分析；崔维孝［13］在总结当前铁路路基防护形式的基础上，进行植物防护、空心砖防护、骨架防护等防护形式下的经济性对比分析，提出防护优化方案，在保证结构稳定的基础上进一步节约了成本。

在黄土地区铁路边坡防护中，为保证骨架结构安全以及在边坡稳定的基础上建立骨架优化方案，应深入开展拱形骨架边坡防护机理的理论研究。基于土坡浅层稳定分析方法，结合骨架受力情况分析其破坏模式，建立边坡稳定安全系数与骨架参数的关系，提出拱形骨架防护下边坡浅层稳定性分析方法，以保证黄土地区在降雨作用下的边坡骨架防护结构的安全性、经济性。

1 工程概况

兰州至张掖三四线铁路黄土路堑高边坡工程项目位于甘肃省兰州市永登县，边坡主要地层岩性为上部的第四系风积砂质黄土和下部泥岩。上部黄土厚度>50 m，土质较均匀，为Ⅱ级普通土；下部泥岩，岩体较完整且岩质较软，为Ⅳ级软石。经调查，该地区全年不同月份降雨量相差较大，呈现夏秋季多、冬季少的不均匀特点，全年最高降雨量可达80 mm，且强降雨频繁。边坡土体结构较差，易受雨水侵蚀，短期强降雨使表层土体含水量迅速升高，抗剪强度迅速下降，边坡浅层稳定受到严重威胁。因此，应采取相应的防护措施，保证路堑高边坡稳定性。

对该地区原状土进行取样并开展三轴压缩试验，测得土体抗剪强度（见表1）。该路堑边坡坡度为1∶1.5，拱形骨架防护结构矢跨比为1∶5。对降雨作用下边坡浅层滑塌的现场情况进行调查，发现滑动深度较浅，约1.5 m。因此，取滑动深度z=1.5 m、侧压力系数K0=0.75、摩擦系数μ=0.35、混凝土重度γc=25 kN/m3。由于黏性土的黏聚力影响，使库伦被动土压力增大。因此，在进行库伦被动土压力计算时，应考虑黏聚力作用，计算与该黏性土抗剪强度相等的无黏性土内摩擦角，将其视为该黏性土体综合内摩擦角。综合内摩擦角可按照式（1）计算，各项土体抗剪强度指标见表1。

表1 土体抗剪强度指标

式中：φ为综合内摩擦角；φ为内摩擦角；c为黏聚力；γ为重度；z为滑动竖向深度，取1.5 m；α为边坡坡面倾角。

2 稳定性分析

骨架结构作为一种边坡防护措施，对于提高边坡浅层稳定性、保证边坡服役性能具有重要作用，其对边坡的防护效应主要体现在加强边坡浅层土体的稳定性。

2.1 无防护土坡浅层

无防护土坡浅层土体结构受力示意见图1。对于土坡某宽度土条，受雨水软化影响竖向滑动深度为z，受相邻土体作用力为E，相互抵消，不会对土体稳定分析产生影响。土体承受抗滑力为R、下滑力为H，由重力沿滑面的分力T、W产生。

图1 无防护土坡浅层土体结构受力示意图

因此，无防护结构的土坡中，浅层稳定安全系数fs计算如下：

2.2 拱形骨架结构防护土坡浅层

拱形骨架防护边坡结构和拱形骨架单元结构分别见图2、图3。沿横骨架浇筑0.1 m×0.1 m 的凸起结构，其中，影响边坡浅层稳定安全系数的拱形骨架结构参数，包括横竖骨架宽度b、骨架埋设深度h、横骨架净距lh、竖骨架净距lv，对于单个拱形骨架防护单元，其防护宽度Lh=lh+b，防护高度Lv=lv+b。

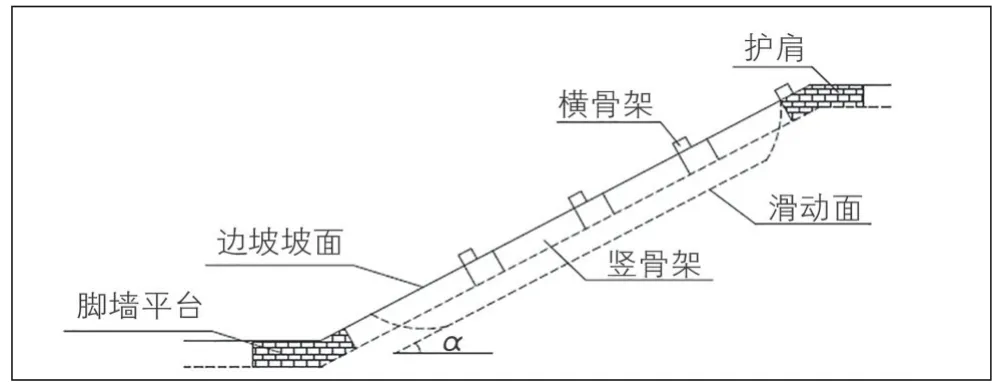
图2 拱形骨架防护边坡结构

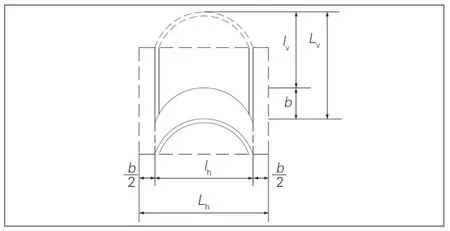
图3 拱形骨架单元结构

边坡滑动土体被拱形骨架结构分割，骨架结构对内部土体的承担作用主要由横骨架自身结构强度及骨架与土体间的摩擦力提供，竖骨架将横骨架承担的荷载进行支撑并传递至脚墙平台。因此，基于无防护顺流土坡浅层分析方法，定义拱形骨架结构防护土坡安全系数Fs为抗滑力与下滑力之比，即：

式中：K1、K2分别为边坡土体替换为相等面积的骨架结构后，对边坡浅层稳定安全系数的提高参数；V1、V2分别为横、竖骨架的体积；p为骨架防护结构的总抗力，主要包括横骨架结构抗力及横竖骨架与土体间的摩擦力。

基于拱形骨架结构防护土坡浅层稳定分析方法，分别考虑横竖骨架宽度b、骨架埋设深度h、横骨架净距lh、竖骨架净距lv等4 个骨架参数对安全系数的影响程度。

3 骨架参数对安全系数的影响

3.1 骨架截面参数对安全系数的影响

骨架截面参数包括横竖骨架宽度b和骨架埋设深度h。根据调查结果，骨架防护结构净距通常选取2～3 m。因此，进行骨架截面参数影响分析时，选取横骨架净距lh=竖骨架净距lv=2.5 m。骨架截面参数对安全系数的影响见图4。

（1）骨架宽度不同。如图4（a）所示，当骨架宽度不变时，安全系数随骨架埋设深度增大而增大，其原因是骨架埋设越深，骨架与土体之间接触越牢固，两者作用效果更强，横骨架挡土抗力更大，边坡土体浅层安全系数得以提高。

（2）骨架埋设深度不同。如图4（b）所示，当骨架埋设深度h>0.2 m 时，安全系数随骨架宽度增大而增大，其原因为增大骨架宽度，使边坡防护结构面积增大、土体面积减小，在增大骨架与土体摩擦力的同时，减小了降雨入渗量，安全系数得以提高；当骨架埋设深度h<0.2 m 时，安全系数随骨架宽度增大而减小，其原因是骨架埋设较浅，骨架结构与土体接触较少，骨架宽度增大造成骨架自质量增大，边坡土体对骨架结构作用效果较弱，横骨架挡土作用减弱，进而导致边坡滑塌。因此，当骨架埋设深度过浅时，增大骨架宽度反而会引起边坡浅层安全系数降低。为保证边坡结构安全，骨架埋设深度≥0.2 m。

骨架宽度和埋设深度的增大都会使安全系数增大，但两者影响程度不同。如图4（c）所示，h-Fs关系曲线相比于b-Fs关系曲线斜率更大，表明骨架埋设深度对安全系数的影响更显著，而骨架宽度会影响骨架与土体的摩擦作用，骨架埋设深度会影响横骨架挡土抗力。因此，横骨架挡土抗力在提高边坡浅层安全系数、保证边坡结构稳定方面起主要作用。

图4 骨架截面参数对安全系数的影响

3.2 骨架净距对安全系数的影响

横骨架净距lh和竖骨架净距lv都是通过影响横骨架挡土抗力来影响边坡安全系数。

（1）竖骨架净距影响。

拱形骨架破坏模式见图5。如图5 所示，对于某竖骨架净距转化阈值lsp，当lvlsp时，为破坏模式Ⅱ，骨架防护边坡破坏模式发生转换，边坡往往由于骨架结构破坏，进而引起滑塌。

图5 拱形骨架破坏模式

骨架结构抗力主要来源于横骨架自身结构提供的挡土抗力和竖骨架的侧壁摩擦力，对于2 种破坏模式，骨架防护承载力计算如下：

式中：EⅠ和EⅡ分别为2种破坏形式下的骨架结构抗力；Ep为库伦被动土压力，即，Kp为库伦被动土压力系数；对于黏性土，内摩擦角应选取综合内摩擦角；F为竖骨架侧壁产生的摩擦力，即F=K0γcosαh2μ。

当lv=lsp时，EⅠ=EⅡ，可通过式（6）、式（7）得到2种破坏模式的转化阈值，即：

式中：θ为破坏模式Ⅱ中滑动破坏面与坡面的夹角。

由式（8）可知，影响转化阈值的骨架参数有横骨架净距和骨架埋设深度，若取横骨架净距为3 m，对于不同骨架埋设深度，其对应破坏模式的转化阈值见表2。

表2 不同埋设深度破坏模式的转化阈值 m

因此，对于横骨架净距为3 m 的拱形骨架防护结构，其竖骨架净距与骨架结构抗力的关系曲线见图6。

图6 lv-E关系曲线

如图6所示，当lvlsp时，为破坏模式Ⅱ，结构抗力大小基本不变，近似为土体被动土压力，其原因为当骨架结构处于破坏模式Ⅱ时，lv较大，使骨架结构防护面积和竖骨架的侧壁摩擦力更大，骨架防护边坡更易出现土体挤压破坏，而非骨架滑动破坏。

（2）横骨架净距影响。

土体荷载作用下的横骨架受力见图7，作用在横骨架上的土体荷载简化为均布荷载q，两端为固定端支承和铰接支承的拱结构，满跨均布荷载作用下的横骨架弯矩见图8。

图7 土体荷载作用下的横骨架受力

如图8 所示，满跨均布荷载作用于两端铰接支承的拱形结构时，其拱顶弯矩最大；当满跨均布荷载作用于两端固定支承的拱形结构时，在拱顶或两侧支座处产生较大弯矩。结合文献［14］提出的拱形结构两端固定支撑时，满跨均布荷载作用下的内力计算方法，得到3 个极限弯矩大小关系：M1>M3>M2。因此，在进行骨架材料强度校核时，应考虑弯矩M1的影响，即：

图8 满跨均布荷载作用下的横骨架弯矩

由于横骨架长度lh远大于骨架宽度b和骨架埋设深度h，在考虑骨架结构内力影响时，弯矩影响作用＞剪力影响作用，仅需考虑弯矩产生的正应力满足自身材料强度要求，即：

（3）骨架净距对安全系数的影响。

经调查发现，骨架防护结构净距通常选取2～3 m，取b=h=0.4 m，分析骨架净距大小对安全系数的影响。骨架净距对安全系数的影响见图9。

图9 骨架净距对安全系数的影响

由图9可知，横竖骨架净距的增大都会引起骨架防护边坡安全系数的减小，故骨架结构越密，边坡结构的安全系数越大；由于lv-Fs关系曲线斜率>lh-Fs关系曲线斜率，表明相对于横骨架净距，竖骨架净距对安全系数的影响更显著。

3 拱形骨架防护边坡结构优化

横竖骨架宽度b、骨架埋设深度h、横骨架净距lh和竖骨架净距lv作为骨架结构参数，不但影响骨架防护边坡浅层稳定，也影响骨架结构单位防护面积所需的材料用量。因此，基于边坡浅层稳定和横骨架结构强度，建立拱形骨架防护边坡结构优化模型，得到最少骨架结构材料用量下的结构参数。单位防护面积下的骨架结构体积V计算如下：

式中：A为骨架结构防护单元面积。

当骨架结构埋设深度h不变时，若lvlsp，为破坏模式Ⅱ，随着lv增大，若要保持骨架结构安全系数不变，则需要增大骨架宽度b以提高横骨架挡土抗力，单位防护面积下的骨架结构体积随lv和b的增大而增大。lv越小，骨架结构竖向排列越密，给现场施工带来不便，因此取lv=lsp为竖骨架净距最优解。

lv=lsp时，不同横骨架净距lh对应的骨架结构优化结果见图10。如图10 所示，g（1）曲线为边坡稳定安全系数不变时的b-h关系曲线，根据实际工程要求，安全系数Fs取1.25。由图可知，当安全系数Fs保持不变时，b与h呈负相关；g（2）曲线为基于骨架结构强度得到的b-h关系曲线，其中，该曲线上方区域包含的b、h值不满足强度要求。因此，g（1）与g（2）曲线交点对应的b、h值为满足边坡浅层稳定和骨架结构强度条件的临界值，该临界值对应的单位防护面积下的骨架结构体积为优化结果Vmin，不同横骨架净距lh对应的临界b、h值及优化结果Vmin见表3。

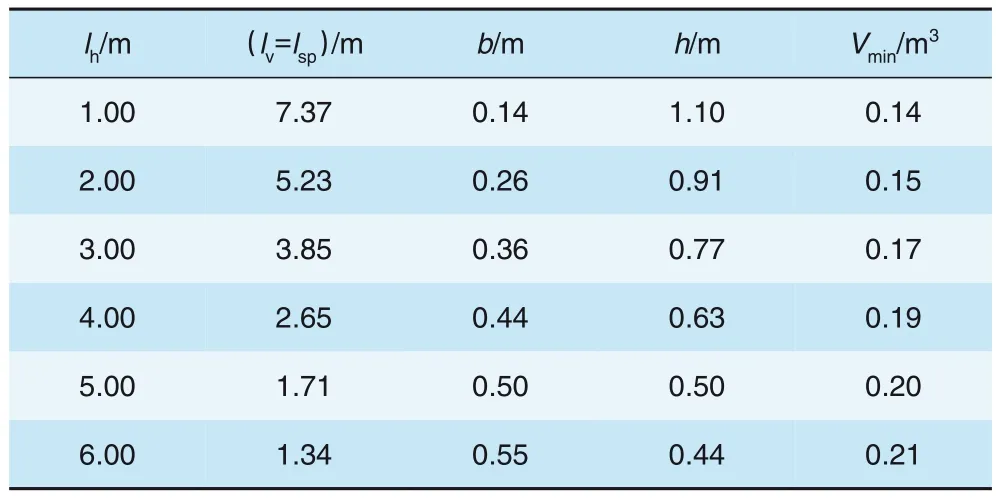
表3 拱形骨架结构尺寸优化结果

图10 骨架结构优化结果

由表3可知，骨架结构宽度越小，Vmin越小。但是，骨架结构宽度过小会影响骨架结构施工质量，实际设计要求规定b≥0.30 m。因此，取b=0.36 m，得到拱形骨架结构优化结果为：lh=3.00 m、lv=3.85 m、h=0.77 m，对应单位防护面积的骨架结构最小体积Vmin=0.17 m。

4 结论

以实际工程为背景，对其在拱形骨架防护作用下的稳定性展开研究，通过分析拱形骨架防护作用的机理以及不同骨架参数对边坡稳定系数的影响程度，在保证边坡安全稳固和骨架强度足够的前提下对拱形骨架进行结构优化研究，得到以下结论：

（1）边坡安全系数与骨架参数有关。当骨架净距保持不变时，横竖骨架宽度b和骨架埋设深度h增大都会引起边坡承载力增大，且骨架埋设深度h对承载力变化影响更大；当横竖骨架宽度b和骨架埋设深度h不变时，安全系数随着骨架净距增大而减小，且横骨架净距影响更大。

（2）对于边坡骨架防护结构，根据竖骨架净距lv的变化，出现2 种不同破坏形式，即单元底部剪切滑动破坏（模式Ⅰ）和骨架挡土结构破坏（模式Ⅱ）。2 种破坏模式间存在转化阈值lsp，当竖骨架净距lsp时，为破坏模式Ⅱ。2 种破坏模式下，骨架防护结构承载能力不同，承载力随着竖骨架净距lv增大而增大，当lv=lsp时，承载能力达到最大，近似于边坡土体库伦被动土压力。

（3）当竖骨架净距达到转化阈值lsp时，为竖骨架净距最优值。依托V与骨架参数的关系，在不同横骨架净距下，分别得到竖骨架净距最优值对应的横竖骨架宽度b与骨架厚度h的关系，基于前提条件确定满足工程施工条件的最小b、h值，此时对应的横骨架净距为最优值，最终得到骨架结构最优参数。