填充石膏基轻质材料的冷弯型钢复合墙体受剪承载力分析
吴函恒,隋 璐,聂少锋,周天华,袁涛涛
(1. 长安大学建筑工程学院,西安 710061;2. 中铁第一勘察设计院集团有限公司,西安 710043)
冷弯型钢结构体系具有自重轻、装配式建造、低碳环保和综合效益高等优点,已经在欧美和日本等国家被广泛使用。近年来,由于我国大力发展和推广装配式建筑[1 − 4],该体系越来越受到青睐。冷弯型钢组合墙体是冷弯型钢结构房屋的主要抗侧力构件,其通常由冷弯型钢龙骨和墙面板(石膏板、OSB板、水泥纤维板和薄钢板等)组成。但由于冷弯型钢组合墙体的抗侧刚度和受剪承载力偏低,限制了建筑层数,冷弯型钢结构仅在低层房屋体系中应用广泛。然而我国人口密集,土地资源紧张,推广多高层冷弯型钢结构房屋更符合我国的国情,因此,提高冷弯型钢组合墙体的抗侧刚度和承载力成为目前亟待解决的问题。
在水平荷载作用下,冷弯型钢组合墙体受力复杂,影响墙体受剪承载力的因素诸多,国内外学者往往通过试验研究来确定墙体的受剪承载力[5 − 7]。Derveni等[8]、Zeynalian等[9 − 10]、Mowrtage等[11]、Fiorino等[12 − 13]分别研究了墙面板类型、螺钉形状、螺钉间距、立柱间距、支撑类型对墙体承载能力的影响;王宇航等[14]对带斜撑冷弯薄壁型钢组合墙体进行试验研究,表明斜撑能够有效提高墙体的承载能力;闫维明等[15]研究了加载方式、墙体开洞尺寸等因素对锁铆连接冷弯型钢开洞组合墙体抗剪承载力的影响。少部分学者通过理论分析来确定墙体的受剪承载力。刘斌等[16]对喷涂式轻质砂浆-冷弯薄壁型钢组合墙体进行了试验研究,并探讨了抗剪承载力设计值的计算方法;郭鹏等[17]根据冷弯型钢骨架墙体两种不同的破坏模式,提出墙体受剪承载力的计算公式。
传统的冷弯型钢组合墙体隔热和隔声性能差,且在两侧墙面板之间形成空腔,影响居住的舒适感和安全感,与中国传统建筑理念相悖。为了解决这一问题,国内学者对带有填充材料的冷弯型钢组合墙体开展了试验研究和理论分析。Xu等[18]对填充轻质泡沫混凝土的冷弯型钢墙体开展试验研究,并提出了墙体抗剪强度的估计算值。郁琦桐等[19]对轻钢龙骨玻化微珠保温砂浆复合墙体进行试验研究,并提出了墙体抗剪承载力的计算方法。田稳苓等[20]对新型泡沫混凝土轻钢龙骨组合墙体试验研究,提出抗剪承载力的计算公式。吴函恒等[21]以石膏基轻质材料为填充物,提出了一种新型冷弯型钢填充式复合墙体,如图1所示。试验研究表明,该填充材料能够明显提高墙体的抗侧性能。
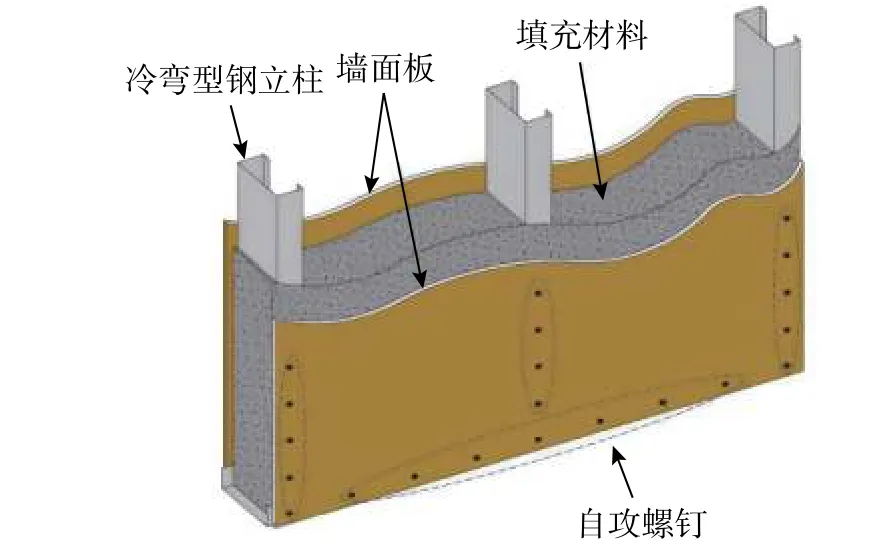
图1 填充石膏基材料的冷弯型钢复合墙体Fig.1 Cold-formed steel composite walls with lightweight gypsum fillings
在课题组试验研究[21 − 22]的基础上,本文分析了传统冷弯型钢复合墙体和填充石膏基轻质材料的冷弯型钢复合墙体的破坏模式,并基于叠加法建立墙体的受剪承载力计算模型,建立复合墙体受剪承载力计算公式,研究结论可为工程应用和规范编制提供参考。
1 试验概况及破坏形态
1.1 试验概况
对3组11片足尺冷弯型钢复合墙体进行低周往复加载试验研究[21 − 22],试件编号和分组情况如表1所示。试件的高度均为3000 mm,宽度均为2400 mm。墙体立柱采用冷弯薄壁C型钢,规格分别为C90×40×14×1.2和C140×40×14×1.5,其中边立柱由2肢冷弯薄壁C型钢背靠背拼合而成,中立柱为单肢冷弯薄壁C型钢。墙体的导轨采用冷弯薄壁U型钢,规格分别为U93×35×1.2和U144×35×1.5。
墙面板分别采用防水石膏板(12 mm厚)和OSB板(9 mm厚)。由于墙面板的产品尺寸(长×宽)为2440 mm ×1220 mm,根据《低层冷弯薄壁型钢房屋建筑技术规程》(JGJ 227−2011)[23]的建议,在墙面板在距离试件底部560 mm处和中立柱处分别设有一道水平拼接缝和竖向拼接缝。同时,为了传递倾覆弯矩和水平剪力,在墙体四角设置抗拔件,并在上下导轨上设置抗剪件。试件构造和详细尺寸如图2所示。
1.2 试件破坏形态
1)空腔墙体
冷弯型钢空腔墙体的抗侧性能主要由墙面板的蒙皮支撑效应来提供,该蒙皮支撑效应一方面取决于墙面板的材料强度和厚度,另一方面取决于冷弯型钢龙骨与墙面板之间螺钉连接的强度。在剪力作用下,螺钉连接处会出现螺钉内陷、螺钉倾斜和墙面板挤压破坏等现象(图3(a)、图3(b)),当达到承载能力的极限状态时,由于自攻螺钉连接破坏致使墙面板与冷弯型钢骨架出现相对滑移,变形不同步,墙面板蒙皮作用丧失。因此,冷弯型钢空腔墙体的破坏形态主要表现为墙面板与冷弯型钢龙骨之间自攻螺钉连接的破坏(图3(c)、图3(d))。

图3 空腔墙体的破坏特征Fig.3 Failure characteristics of unfilled specimens
2)填充式墙体
除了墙面板提供蒙皮支撑效应外,石膏基轻质材料作为填充物可为墙体提供抗侧刚度和承载能力。由于填充材料被冷弯型钢龙骨划分成若干块,在剪力作用下,各填充块形成斜向受压带,最终出现角部被压碎的破坏形态(图4(a))。而试件HS-90-3和HS-90-4的破坏却出现在冷弯型钢立柱与导轨的连接部位,墙体骨架丧失了对填充材料的约束作用,从而导致填充材料支撑效应的失效。产生上述现象的原因为:HS-90-3和HS-90-4填充材料的强度较HS-90-2偏高,而冷弯型钢龙骨的截面尺寸较140系列偏小,墙体骨架先于填充材料发生破坏。而除HS-90-3和HS-90-4外,其余填充式墙体的破坏模式均为填充材料的角部压碎。因此,填充式墙体的破坏模式可归纳为两类:一类为填充材料的角部压碎(图4(a));另一类为冷弯型钢龙骨的破坏(图4(b))。当填充材料的强度偏低、龙骨的截面尺寸偏大时,易于发生填充材料的破坏;当填充材料的强度偏高、龙骨的截面尺寸偏小时,易于发生冷弯型钢龙骨的破坏。各墙体试件的破坏模式如表2所示。

图4 填充式墙体的破坏特征Fig.4 Failure characteristics of infill specimens
2 受剪承载力分析
2.1 承载力模型
由冷弯型钢填充式墙体的破坏形态可知,当墙体达到承载能力的极限状态时,蒙皮支撑效应和填充材料的支撑效应均已失效。根据极限平衡理论,建立基于叠加法的受剪承载力计算公式,可用于计算填充式墙体的受剪承载力,其表达式为:

式中:Vu为填充式墙体的受剪承载力;VSu为墙面板蒙皮支撑效应对受剪承载力的贡献;VGu为填充材料支撑效应对受剪承载力的贡献。
2.2 墙面板蒙皮效应的贡献VSu
从破坏模式来看,墙面板和冷弯型钢龙骨之间螺钉连接的破坏导致了蒙皮支撑效应的失效。因此螺钉连接的强度决定了蒙皮支撑效应对墙体受剪承载力的贡献。采用整体分析法,考虑所有螺钉受力对墙体受剪承载力的影响,分析时,提出基本假定如下(图5):
1)墙体上端和下端(导轨)的自攻螺钉所承担的剪力可以分解为沿着X方向的水平分量Fex和沿着Y方向的竖向分量Feyi,沿着X方向的水平分

根据合力方程,墙体上(下)端自攻螺钉所承担的剪力为:
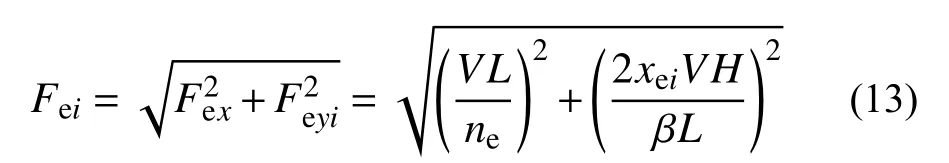
根据式(10)和式(13),墙体上(下)端单颗螺钉所承担的剪力Fei、墙体左(右)侧边上单颗螺钉所承担的剪力Fs分别与单位长度墙体所承受的剪力V的之比值可表述为:

当墙面板与冷弯型钢龙骨之间的自攻螺钉连接发生剪切破坏时,墙面板的蒙皮支撑效应为墙体提供的承载能力达到极限状态。因此,由式(14)和式(15)可以得到墙面板蒙皮支撑效应贡献VSu的计算式为:

式中:Pu为由“冷弯型钢—单颗自攻螺钉—墙面板”连接体的剪切强度,取课题组的相关试验数据[24];αmax为αs和αei的较大值,即αmax=max{αs,αei};η为考虑墙面板拼接滑移效应的折减系数。
采用空腔墙体(HS-90-1、HS-140-1)和文献[25]中的试验数据来确定折减系数η,相关试验值和通过式(16)得到的理论计算值如表3所示。从表中可以看出:折减系数η的变化范围在0.896~0.947,综合设计考虑,折减系数建议取为0.9。则墙面板蒙皮支撑效应对墙体受剪承载力的贡献可按式(17)计算。
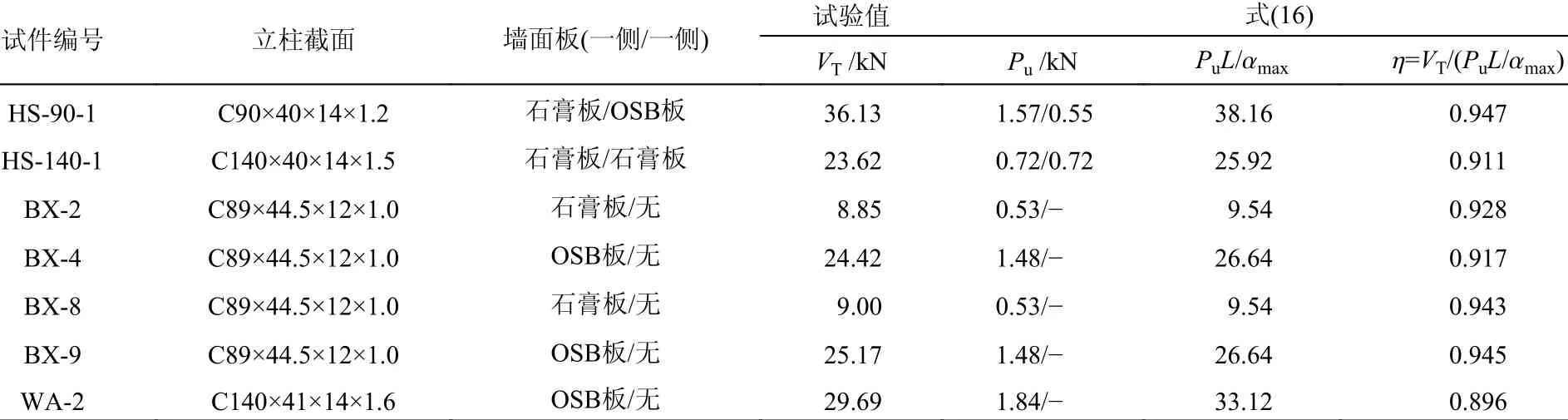
表3 考虑墙面板拼接滑移效应的折减系数ηTable 3 Reduction factor η considering the seam slipping of wall boards

2.3 填充材料支撑效应的贡献VGu
1.2节表明:当填充材料对墙体的支撑效应失效时,墙体存在两种破坏模式:一种为填充材料的角部被压碎,填充块失去支撑作用;另一种为墙体龙骨的破坏,导致墙架对填充材料块的约束作用丧失。由于填充材料的抗拉强度较低,且填充块与冷弯型钢墙架之间的交界面上没有设置连接件。因此,在侧向力作用下,该交界面并不能传递拉应力,填充块与冷弯型钢墙架之间的相关作用力只存在于斜向受压区,如图6所示。填充块与墙架的受压交界面上存在正应力(σh,σv)和剪应力(τh,τv)。基于此,当分析填充块与冷弯型钢墙架之间的相关作用时,提出以下假定:
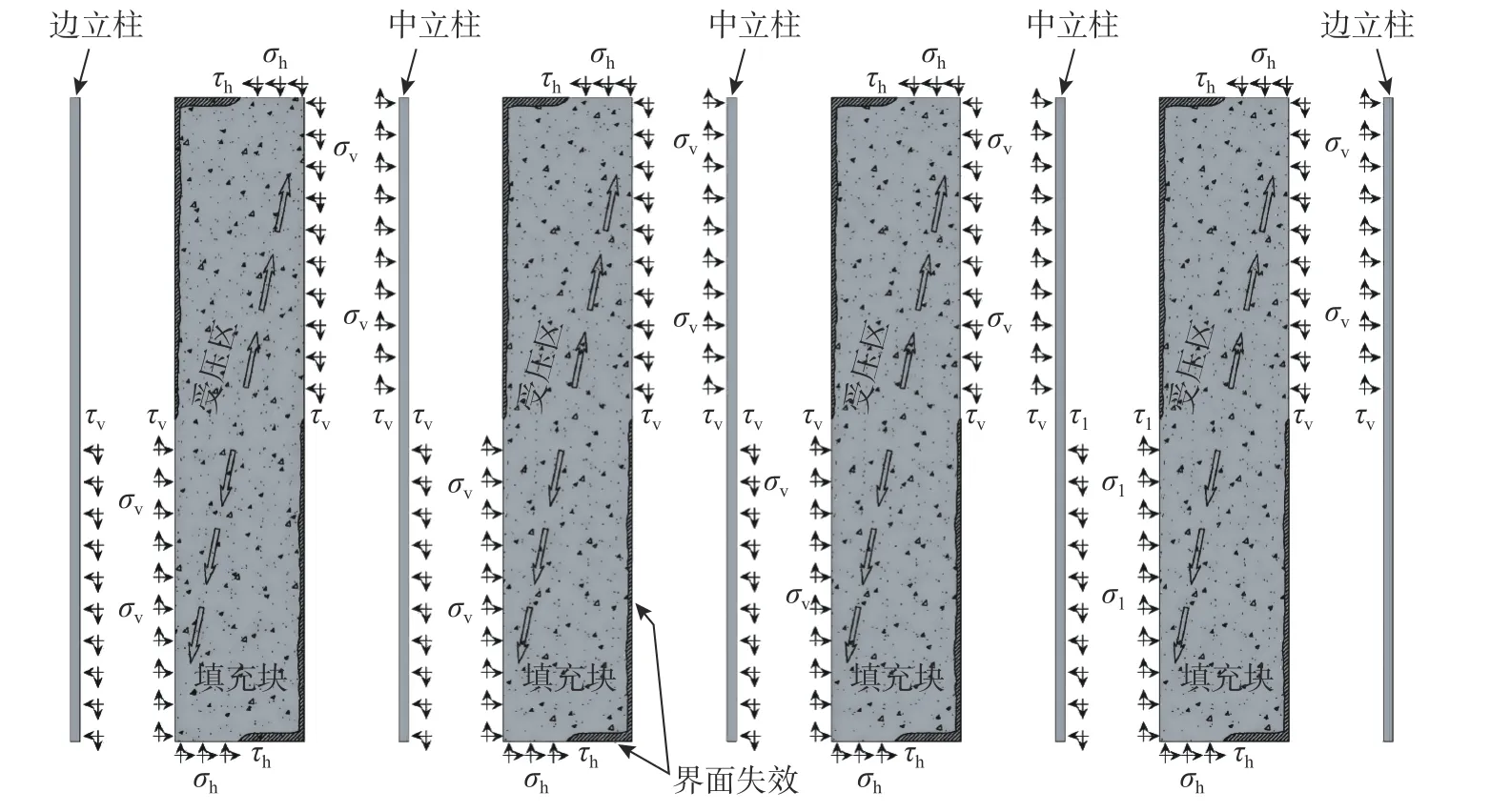
图6 填充块和冷弯型钢龙骨之间的相关作用力Fig.6 Interaction forces between gypsum pieces and CFS studs
1)由于填充块的高宽比较大,忽略填充块顶部和底部受压界面上的正应力σh和剪应力τh;
2)假定填充块竖向受压区高度为x,该受压界面上的正应力σv和剪应力τv沿着高度x均匀分布,如图7所示;
3)如图7所示,n−1个中立柱和2个边立柱将所承受的水平力传递给每个填充块,每个中立柱的上下端均承担正应力和剪应力,而两个边立柱只有上端或下端承担正应力和剪应力,因此两个边立柱的受力之和与单个中立柱所承担的力相同。假定每个填充块受力相同,则每个中立柱(相当于两个边立柱之和)传递的剪力为P/n。而边立柱顶端和底端传递的剪力分别为PR和PL。
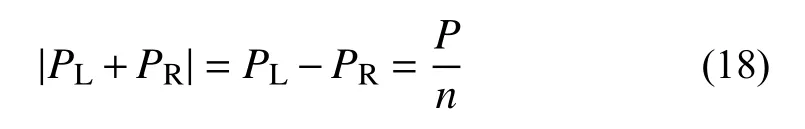
如图7所示,对每个填充块任意一个角点建立弯矩平衡方程,如式(19)所示:
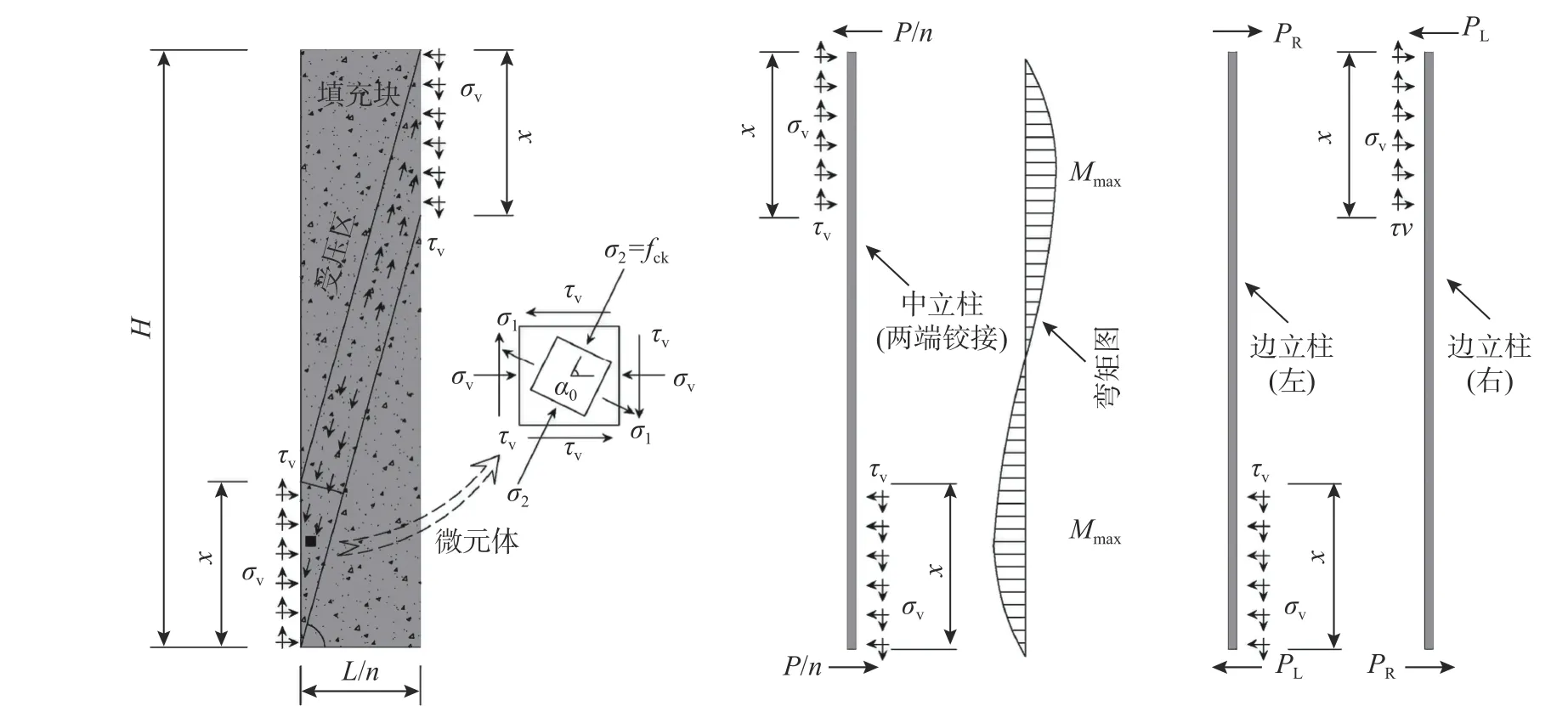
图7 受剪承载力计算模型Fig.7 Calculation model of shear bearing capacity

式中:t为填充块的厚度;σv为填充块竖向正应力;τv为填充块竖向剪应力。
同时,建立中立柱上端点或下端点的弯矩平衡方程,如式(20)所示:

简化式(20),可得式(21):

分别对边立柱的上、下端点建立弯矩平衡方程,可得如下关系式:

将式(22)与式(23)作差,可得:

基于两种破坏模式,分别研究填充材料支撑效应对墙体受剪承载力的影响。
1)填充块角部受压破坏
探视的时间快要过去了,管教干部已进来提醒。一直跟儿子对峙着的父亲这才掉过头来。我发现他与刚才的强悍判若两人,竟是一脸的悲戚。他低声说:“里面的日子不好过,看他黑了,也瘦了。”
如图7所示,在压应力σv和剪应力τv的作用下,取填充块角部的微元体进行分析,其主应力分别为:

式中:σ1为主拉应力;σ2为主压应力。
根据第一强度理论,当填充块角部压碎时,主压应力σ2等于填充材料的抗压强度fck,即:
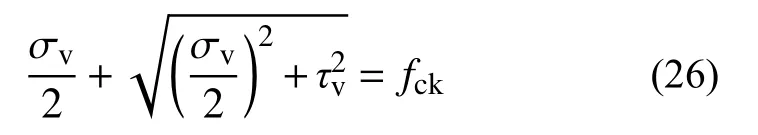
从图7可以看出,α0为主压应力σ2和微元体水平方向的夹角。通过平面应力分析可得:

为了确保斜向受压带的方向与主压应力σ2的方向一致,由图形关系得出:

联立式(27)和式(28),消除α0,可得:
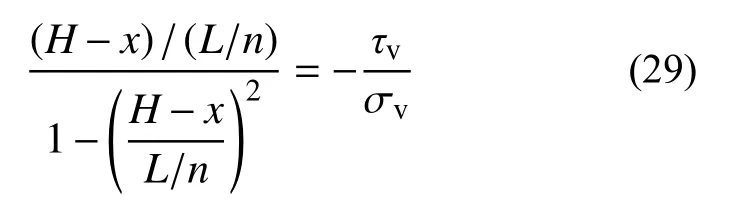
联立式(19),式(21)和式(29),可得式(30):
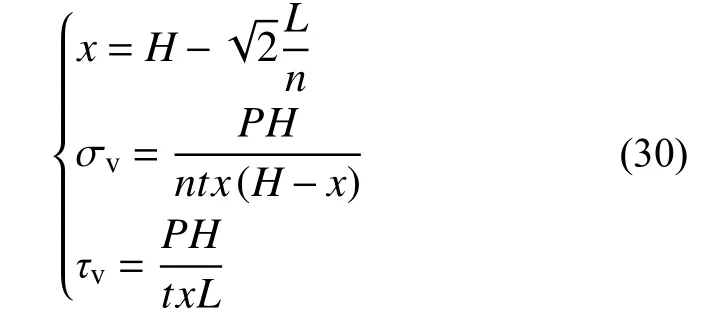
将式(30)代入式(26),可以得到填充材料支撑效应对墙体受剪承载力的贡献:
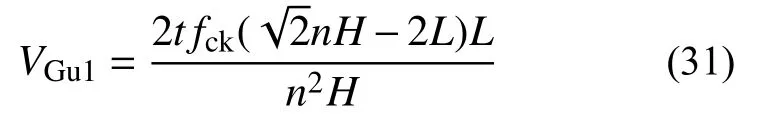
2)冷弯型钢立柱的弯曲破坏
假定冷弯型钢立柱为两端铰接,在正应力σv的挤压作用下,立柱的弯矩分布如图7所示。立柱任意一点的高度定义为l,则沿高度l方向上任意一点的弯矩可表示为:
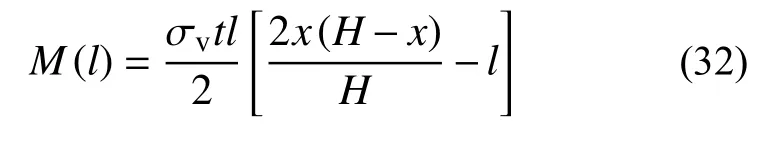
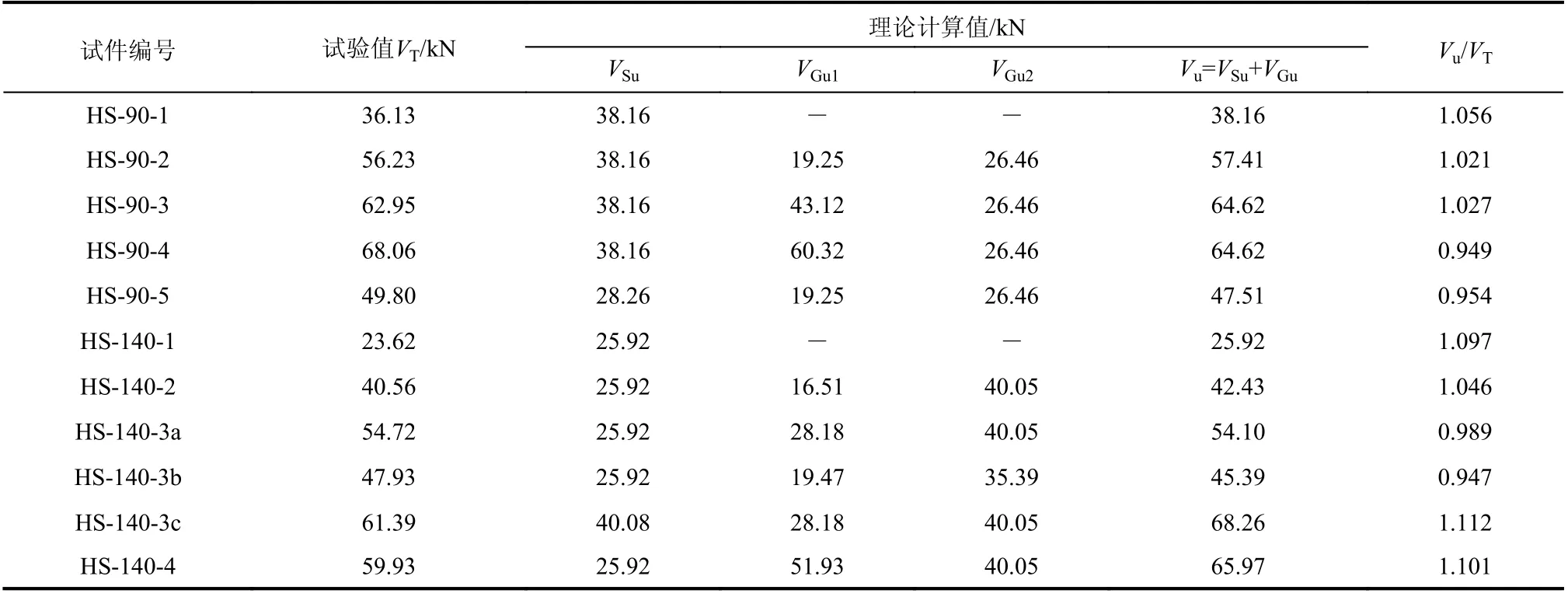
当l=x(H−x)/H 当立柱承担的最大弯矩M(l)max达到极限弯矩Mu时,立柱发生弯曲破坏,即: 将式(30)代入式(34),可得墙体的受剪承载力为: 由文献[26]可知,由于填充材料的包裹效应,冷弯薄壁型钢立柱在屈服之前不发生局部屈曲,因此以边缘纤维屈服作为立柱受弯的极限状态,则立柱的极限弯矩可以表达为: 式中:Wx为冷弯型钢立柱的全截面模量;fy为钢材的屈服强度。 最终,填充材料支撑效应对墙体受剪承载力的贡献取VGu1和VGu2的最小值,即: 为了验证上述计算方法的准确性,将墙体受剪承载力的计算值和试验结果进行对比,结果如表4所示。从表中可以看出,计算值和试验值的比值在0.947~1.112,表明该方法能够较为准确地预测填充石膏基轻质材料的冷弯型钢组合墙体的受剪承载力。 由表4可以看出,对填充材料强度偏低的墙体(HS-90-2、HS-90-5、HS-140-2、HS-140-3),VGu1的计算值小于VGu2的计算值,这表明填充材料先于冷弯型钢立柱破坏,而对于填充材料强度偏高的墙体(HS-90-3、HS-90-4、HS-140-4),VGu2的计算值小于VGu1的计算值,这表明冷弯型钢立柱先于填充材料破坏。因此,提高填充材料的强度并不能一直提高墙体的受剪承载力,反容易使冷弯型钢立柱先行发生破坏。由于,在实际使用中冷弯型钢立柱还需要承担竖向荷载,因此,建议通过设计避免冷弯型钢立柱发生先行破坏,即: 表4 受剪承载力计算值与试验值对比Table 4 Comparisons of shear capacity between test values and calculated values 将式(31)和式(35)代入式(38),填充材料的抗压强度建议满足下式,即: 在试验研究的基础上,对传统冷弯型钢空腔墙体和和填充石膏基轻质材料的冷弯型钢复合墙体的破坏形态进行分析,并提出填充式墙体的受剪承载力计算方法,主要结论如下: (1) 填充材料的使用能够显著地提高冷弯型钢复合墙体的受剪承载力,填充式墙体的破坏模式包括墙面板蒙皮作用失效和填充材料支撑效应的失效。 (2) 当填充材料支撑效应失效时,会出现两类破坏模式:一类为填充块角部受压破坏;另一种为冷弯型钢立柱的破坏。强度偏高的填充材料容易使冷弯型钢立柱发生破坏。 (3) 考虑到墙面板蒙皮效应和填充材料支撑效应对墙体抗剪承载力的贡献,提出了基于叠加法的受剪承载力计算公式,将理论计算值与试验值进行对比,结果表明:采用本文的计算方法,能较好地预测填充式冷弯型钢墙体的受剪承载力。
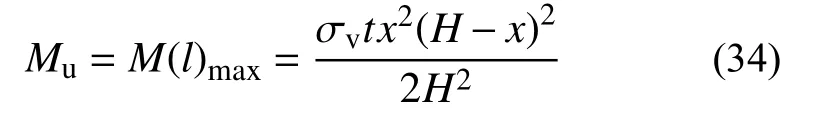



3 正确性验证

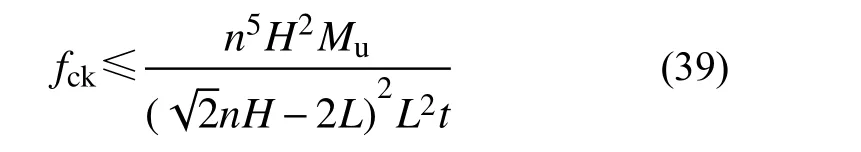
4 结论

