水泥混凝土路面板早龄期徐变效应研究

胡昌斌，孙增华，王丽娟

(福州大学土木工程学院，福建，福州，350008)

水泥混凝土路面板早龄期阶段由于受到水化热、环境因素影响，会在板内产生非线性温度梯度和湿度梯度，产生温度翘曲、湿度卷曲和内应力[1−3]，显著影响路面的耐久性和长期性能[4−6]。徐变作为混凝土的固有材料特性，会对路面板早龄期初始性状、翘曲变形和应力产生松弛影响效应，进而影响路面早期和长期性能。

混凝土早期徐变的产生机制是混凝土内水泥凝胶体层间空隙结构及内部水分移动等微观结构变化的综合响应[7]，受到混凝土水灰比[8]、温湿度条件[4−10]、应力强度比与加载龄期[11]、拉压应力状态[12]等因素显著影响。早期混凝土徐变作用非常显著，而成熟期阶段徐变表现为一种非常缓慢的过程[2]。

为描述和预测混凝土徐变行为，学者们提出了渗流理论、塑性流动理论、粘性流动理论、粘弹性(滞弹性)理论、微裂缝理论[10]、固化理论[13−15]和微预应力-固结理论[16−17]等，并逐步完善了对混凝土徐变机理解释和徐变计算理论与模型建立[18]。

徐变对路面结构性能的影响研究分为试验研究和基于数值仿真的理论研究两个方面。试验方面，Hansen等[4]基于零应力温度的概念发现徐变提高了高温天气施工路面板零应力温度，降低了低温天气下零应力温度；Yeon等[6]基于徐变系数的步进法和现场试验发现高温环境条件施工的路面板早龄期应力在徐变下松弛60%，低温工况下，徐变松弛早龄期应力松弛50%。

理论研究方面，1984年国内严作人[19]利用有效模量法建立考虑徐变的路面板温度应力计算公式，发现徐变降低温度应力峰值约29%；美国HIPERPAV利用Westman徐变预估模型采用松弛系数法，分析发现徐变使路面应力峰值下降约60%[20]；张君等[21−22]采用应力松弛系数法分别建立了考虑徐变效应的非线性温度应力和湿度收缩应力计算方法，发现徐变松弛应力约40%；魏亚等[23]采用徐变函数结合ABAQUS程序分析发现徐变分别松弛了湿度翘曲和湿度应力36%和45%；Lee等[24]采用GKM模型建立1/4路面结构三维有限元分析模型，发现徐变松弛应力峰值66%，位移峰值下降约50%，胡昌斌等[25]采用GKM模型对整板结构早龄期性状行为分析发现徐变降低早龄期翘曲82%。

以上徐变效应研究显示，徐变对路面板的早期变形和初始应力有显著的松弛效应，应力松弛量级甚至达到1 MPa以上，同时也会影响初始变形和初始应力的分布[23,25]。目前徐变效应已作为路面早龄期行为分析的5个重要参数之一被列入重要的效应研究对象[1−2]。一方面拟通过深刻揭示早龄期阶段的路面板结构的徐变效应和规律，获得路面板的力学计算基准值[1−4]，同时也可以理论指导路面工程实践在结构、材料设计和施工设计，加以利用，提升水泥混凝土路面的性能。

综合目前路面板早龄期徐变效应理论研究可以看到，目前的徐变模型相对简化，许多性质和因素还没有描述，特别是环境场的影响；在结构方面也缺乏早龄期三维结构徐变效应的认识。目前相关研究采用的徐变模型：一类是解析理论研究采用的松弛系数法或徐变系数法[19−23]；另一类是数值分析广泛采用的基于流变学理论的广义麦克斯韦链模型(GMM)、广义开尔文链模型(GKM)等徐变模型[24−25]。以上这两类模型都没有和实际的施工材料、施工环境参数直接挂钩，特别是不能很好考虑现场的温湿度的影响。三维早龄期结构行为仿真分析的缺失和理论模型的简化，直接阻碍了理论机制上对路面板早龄期徐变的三维结构效应、具体材料、环境参数的理论影响和敏感性的掌握，也直接阻碍了路面早龄期徐变理论在结构设计、材料设计和施工环境控制方面的工程应用。

鉴于以上，本文拟优化徐变模型，采用Bažant等[16−17]提出的考虑温度和湿度影响的微预应力-固结理论徐变模型，综合考虑材料、结构及环境等影响因素，建立考虑结构约束的三维路面板早龄期力学行为数值仿真程序，重点对路面板三维结构早龄期徐变效应机制，具体结构、材料、施工环境等参数的影响规律和敏感性进行揭示，厘清徐变对路面板早龄期翘曲和应力的影响机制。

1 路面早龄期性状数值仿真程序建立

1.1 Bažant微预应力-固结理论徐变模型

Bažant等[16−17]在GKM模型基础上，提出微预应力-固结理论模型。该模型考虑了温度和湿度对混凝土徐变特性的影响，通过引入等效龄期、缩减时间变量，统一了变化的温、湿度条件对混凝土徐变的影响，可有效反映现场实际条件下温、湿度对混凝土徐变特性的影响及其作用效应。

根据微预应力-固结理论，单轴应力作用下，混凝土总应变由6部分应变组成(如图1所示)，即：

图1 流变模型Fig.1 Rheological model

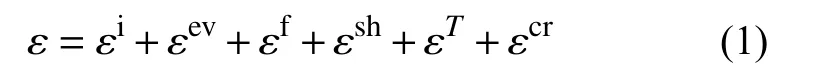
式中： εi为瞬时应变； εev为粘弹性应变； εf为纯粘性应变； εsh为湿度应变； εT为温度应变； εcr为由于混凝土内部裂缝引起的非弹性应变。

研究显示，温度升高显著增大徐变作用[9,26−27]，微预应力-固结理论通过引入两个时间参数来描述温湿度的影响：一是等效龄期te，反映温湿度的影响；二是缩减时间tr，描述温湿度对微结构尺度上层间破坏与恢复速率的影响。te、tr表达式如下：

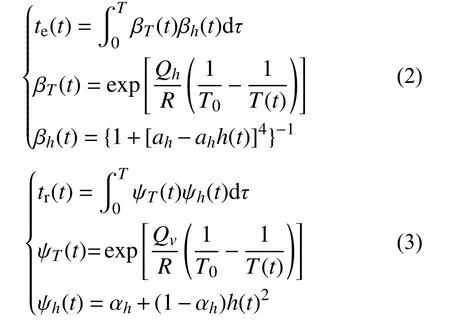
式中：T为绝对温度；T0为参考温度；h为砂浆毛细孔湿度；R为气体常数；Qh为水化过程中的活化能；Qv为粘性生长过程中的活化能；ah、 αh为常数。

为进行有限元数值计算，需要建立增量应力应变关系。粘弹性应变 εev和纯粘性应变 εf呈非线性，为此，需要将各应变分量或控制各应变分量的主要变量变换成一阶微分方程形式。

根据增量形式 Δεev=Δγn/ve,m可得粘弹性应变εev的增量形式表达为：

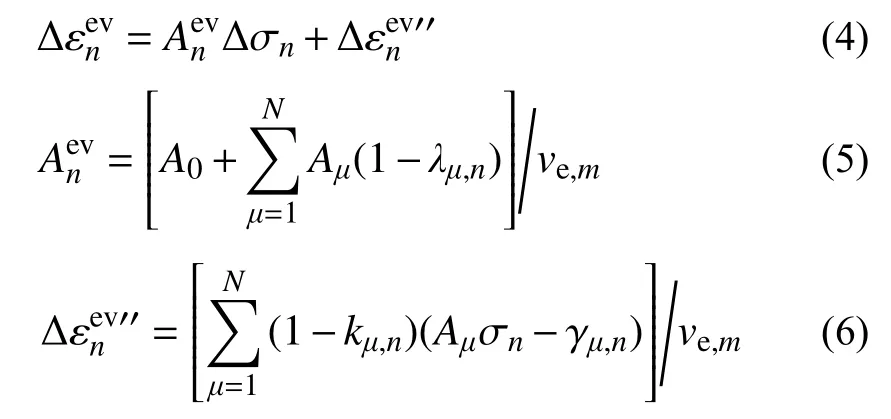
式中：N为Kelvin链单元的个数；kμ,n=exp(-Δyμ,n)，Δyμ,n=ψ(tn+1/2)Δtn/τμ，τμ为Kelvin链第μ个单元的延迟时间；Aμ为Kelvin链第μ个单元弹簧刚度；m=n+1/2，ve,m为混凝土水化过程中固结物质的体积分数； γμ为Kelvin单元的应变，假定时间增量步Δt=tn+1+tn内，应力 σ保持不变，积分得到：

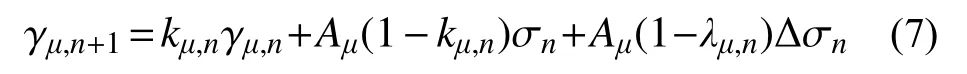
式中，Δ σn=σn+1-σn，γμ,n+1=γμ(tn+1) ， γμ,n=γμ(tn)，ψm=ψ(tn+1/2) ，λμ,n=(1-kμ,n)/Δγμ,n。

利用中心差值积分，纯粘性应变增量形式为：

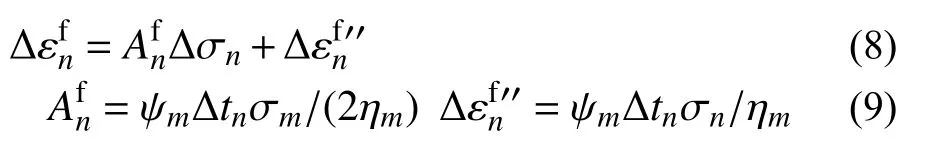
式中， ψm=ψ(tn+1/2) ， ηm=η(Sm) ，Sm=S(tn+1/2)，σm=σ(tn+1/2)=σn+Δσn/2。为得到粘性应变增量，还需得到tn+1/2时刻的微预应力值S(tn+1/2)，根据中心差分法，设S(tn+1/2)=Sn+ΔSn/2，得：

对于裂缝损伤应变 εcr，通过指数算法积分，认为时间增量步内Ccr、Ccr′、εcr′保持不变，可得到：

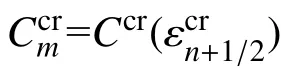
综上可得混凝土应力-应变的增量关系为：

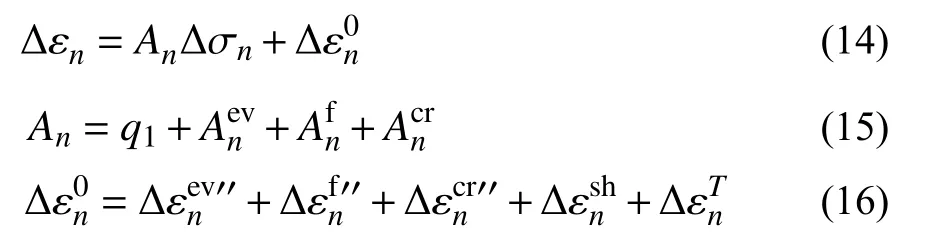
微预应力-固结理论模型的自由参数包括q1、q2、 α 、q4、c和k1，q1与 瞬 时 应 变 εi有 关，q2、α与粘弹性应变 εev有关，q4、c和k1与纯粘性应变 εf有关，均通过徐变试验确定。采用有限单元法编制路面三维仿真程序时，假定单元材料各向同性，上述关系式均转换为ε 、 σ 、 γ 、 εev′′、 εf′′、εcr′′等张量形式，并结合弹性矩阵D和徐变泊松比矩阵C建立应力-应变张量关系。

1.2 三维不均匀温度场模型建立

路面板温度场模拟采用胡昌斌等[28]提出的路面早龄期温度场程序。为反映路面板在现场实际复杂环境条件下的三维不均匀温度场，本文考虑了三维热传导。三维温度场模拟需考虑传热源更为复杂，各离散体单元热源包括水化热、相邻单元热传导、太阳辐射、大气热交换、蒸发散热、基层热传导。各不同位置单元示意如图2，代表不同的热源组成。

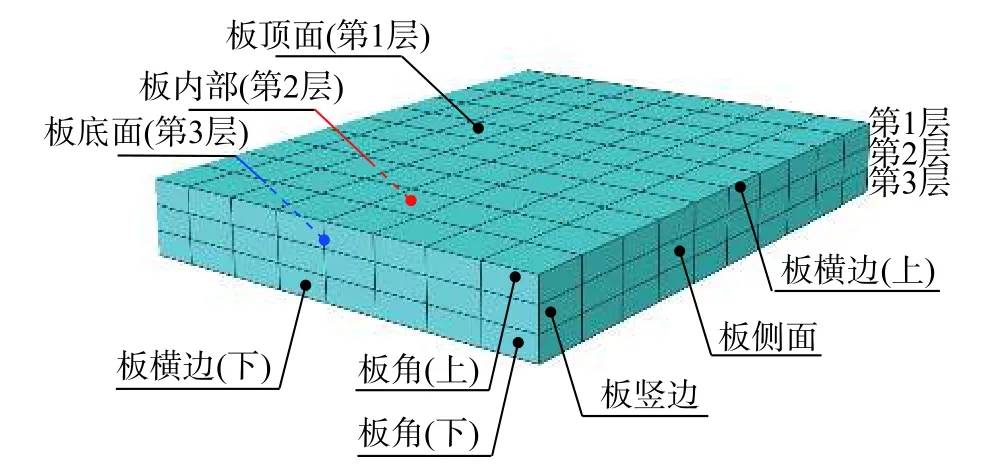
图2 路面板混凝土位置分类示意图Fig.2 Classification of element position of slab

图3示意了温度场仿真程序分别基于二维热传导和三维热传导时路面板整体温度分布的对比，基于三维热传导理论建立的温度场仿真程序能够更好地模拟路面板在复杂环境条件下的三维不均匀特性，与实际工况更为吻合。

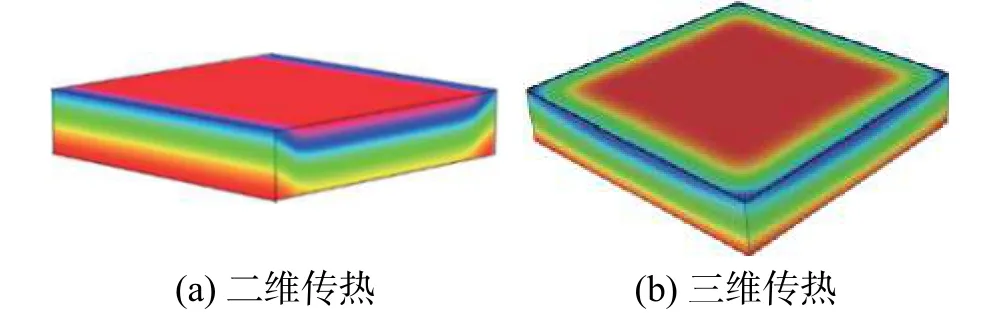
图3 温度场数值模拟技术改进前后对比Fig.3 Comparison of temperature before and after improvement

与文献[28]中的二维温度场数值程序相比，三维不均匀路面温度场模拟仅在各单元热传导平衡方程上存在不同，三维温度场数值模拟程序中水化放热、气温、太阳辐射、水分蒸发等参数模型选取及相关参数取值见文献[28]。

1.3 结构约束模型选取

路面板结构约束主要包括接缝接触面约束和板底与基层之间的接触面约束，本文选用Barbero等[29]对复合多层板的层间接触本构描述为理论基础的界面接触本构模型，分为法向接触模型和切向接触模型，模型如图4所示。

图4 界面接触本构模型示意Fig.4 Interface contact constitutive model

有限元法对接触面的模拟，主要有薄层接触单元和厚度为0的接触单元两种方法。鉴于薄层接触单元计算接触力精度较低，而零厚度单元适合接触面的罚刚度模型，计算精度可保证[30]，本文采用零厚度单元模拟接触面的约束。

1.4 有限元模型建立

通过ABAQUS软件对单块板的路面结构模型尺寸进行预分析，并结合程序的计算效率，确定路面板结构模型尺寸与单元大小，如图5所示。面层、基层和路基采用实体单元C3D8，层间接触和面层四周约束采用零厚度接触面单元I3D8。路基底面固定约束，侧面采用水平方向固定约束。

图5 路面结构有限单元模型Fig.5 Finite element model of pavement structure

综上，并结合已有的路面早龄期湿度场模拟程序FZU-JPEM[31]、张君湿度应变预估模型[32]，基于Fortran平台编制建立了路面板早龄期力学行为仿真程序FZU-SLAB。程序框架与基本流程如图6所示。

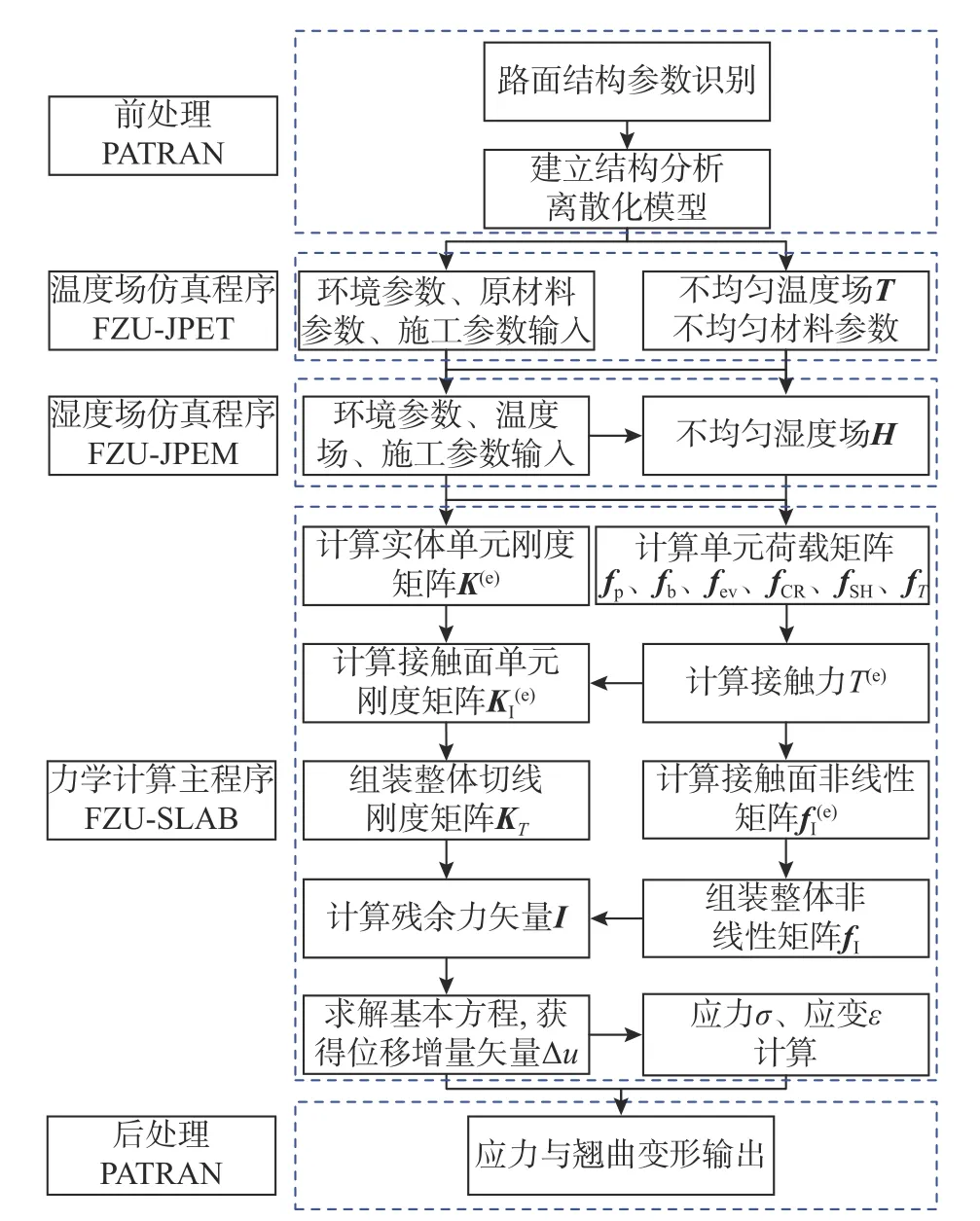
图6 程序框架与计算流程Fig.6 Program framework and calculation process

2 模型参数与分析工况

2.1 徐变模型参数

对于常温下混凝土基本徐变，微预应力-固结理论徐变模型可简化为B3模型[14]，包含了参数q1、q2、q3、q4，且 α=q2/q3，通过常 温徐变试验结果确定参数q1～q4和 α[17,27]。微预应力-固结理论在基本徐变的基础上增加参数c、c0和k1，且c0=2c/q4，通过变温试验结果瞬态分析确定参数c和k1。

室内试件试验分为表面密封、非密封2组，采用位移传感器LVDT监测早龄期混凝土在恒定荷载作用下的变形，同步监测无加载状态下的自由收缩应变和湿度收缩应变。室内试验方案见表1。

表1 试验方案Table 1 Testing program

通过徐变试验结果和B3模型[14]确定q1、q2、q4和 α，对于参数c和k1，Bažant等[17]对不同温度下徐变试验拟合结果表明，c值变化小，为1×10−8MPa−1·d−1～3×10−8MPa−1·d−1，而k1不变，为3 MPa·K−1。通过对上述参数敏感性分析发现，参数c和k1对徐变结果影响很小。因此，参数c和k1取值采用Bažant的试验结果，c取1×10−8MPa−1·d−1，k1取3 MPa·K−1。

此外由于拉压徐变存在异性，根据徐变机理，对非老化流变柔度参数进行修正，令压缩徐变参数，且k取2时，压缩徐变模拟精度较高。

同时结合魏亚等[27]采用的最小二乘法，调整参数取值，寻找最优计算参数，使测量应变结果与计算结果偏差较小，所得徐变模型参数见表2。

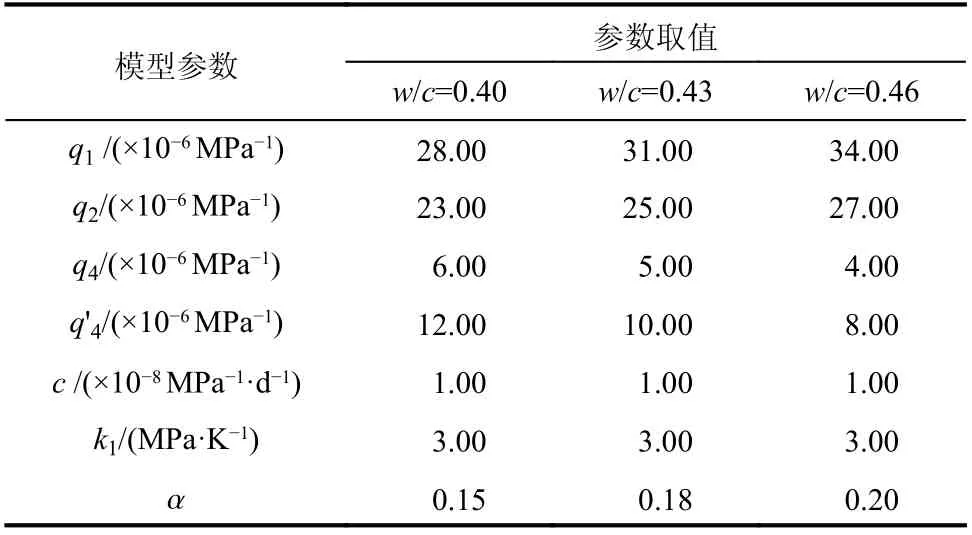
表2 徐变模型参数取值Table 2 Parameter value of creep model

混凝土徐变函数试验结果与计算结果如图7所示，可以看出徐变函数计算结果与实测结果较为吻合。

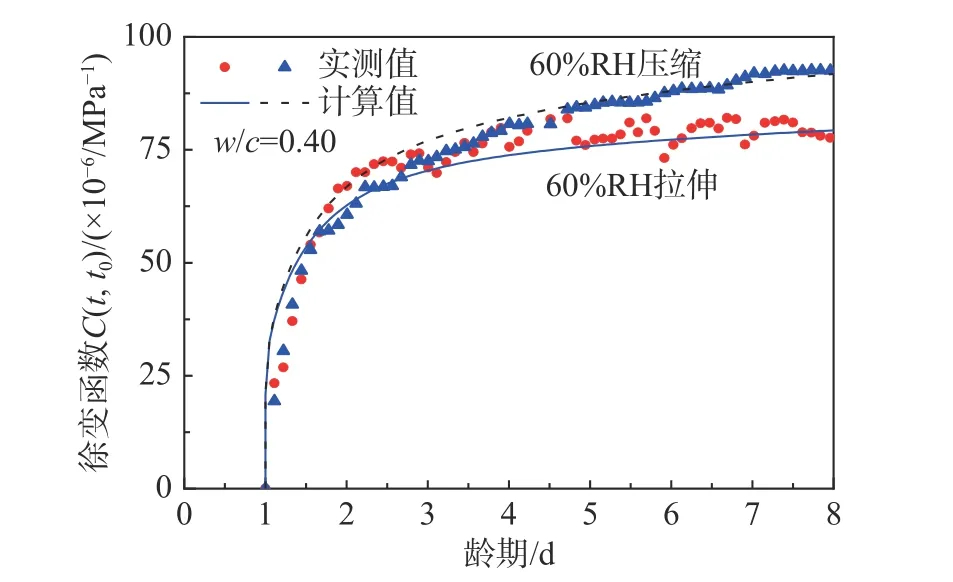
图7 试验结果与计算仿真结果对比Fig.7 Comparison between experimental and numerical data

此外，受压混凝土试件的总应变试验结果和程序计算结果的对比如图8所示。将实测结果的应变初始值叠加混凝土1 d龄期之前的应变调整值Δε0后，应变试验值与计算结果也较为吻合。

图8 总应变试验与模拟验证Fig.8 Experiment and numerical simulation of total strain

2.2 结构模型参数

三维路面结构模型参数主要包括结构参数、材料参数和结构约束参数，见表3，各参数取值均为其取值范围内的典型代表值[25,33−34]。本文第4部分对主要参数取值进行了敏感性分析。

表3 结构模型与材料参数Table 3 Parameters of structural model and materials

2.3 分析工况

徐变效应分析内容包括徐变对无约束和有约束路面板早龄期翘曲和应力的影响效应，以及温、湿度条件与材料对徐变效应的影响性质，分析对比工况设计见表4。分析时，路面温度荷载选取福州高温夏季早上施工工况；湿度荷载考虑了早龄期不利的不可逆干缩[35]，并简化为板顶板底湿度梯度差(忽略湿度梯度昼夜波动)，温、湿度荷载如图9所示。

表4 徐变效应分析工况设计Table 4 Case designing of creep effect analysis

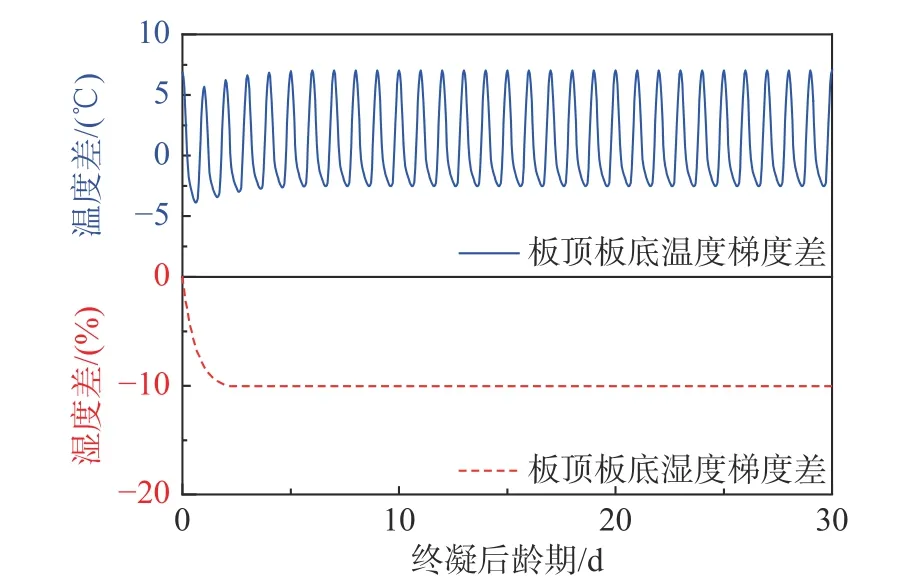
图9 温、湿度荷载Fig.9 Temperature and humidity loading

3 路面板三维徐变效应与性质分析

3.1 无约束路面板结构三维徐变效应

首先以4个板边均无约束的路面板为基准，分析路面板结构三维徐变效应。图10为夏季典型温、湿度荷载共同作用下四边无约束路面板的翘曲和应力时程，图11和图12分别为60 d龄期时翘曲应力峰值对应时刻的翘曲与应力分布状态。

图10 徐变对路面板结构翘曲与应力的影响Fig.10 Effect of creep on curling and stress of pavement slab

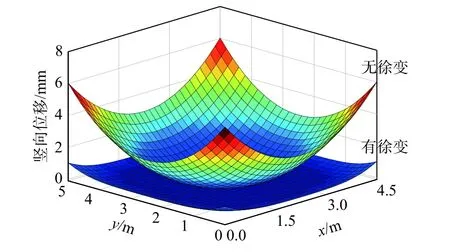
图11 徐变对路面板翘曲形状的影响Fig.11 Effect of creep on curling shape of pavement slab

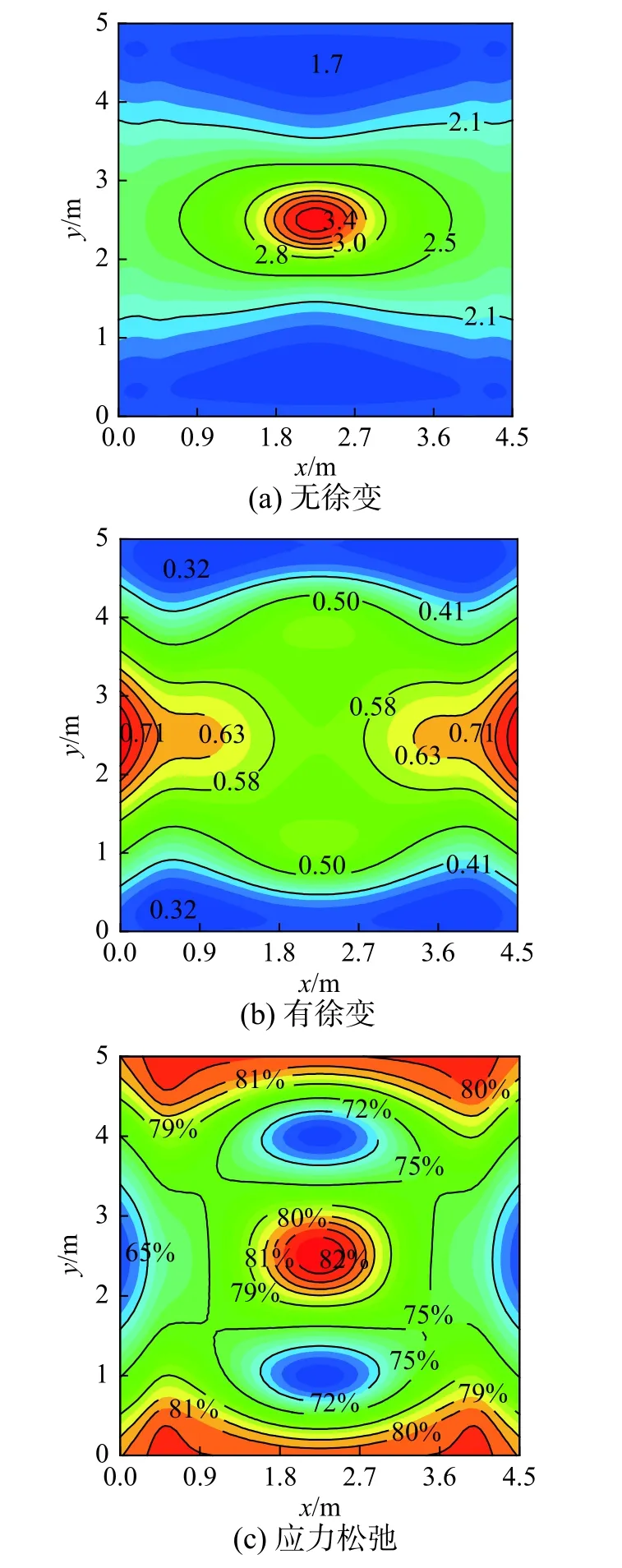
图12 板顶应力与徐变应力松弛分布 /MPaFig.12 Distribution of stress and stress relaxation at slab top

分析图10～图12发现：

1)徐变显著降低了路面板的板角翘曲和应力峰值。60 d龄期时，不考虑徐变下翘曲峰值为6.2 mm，板顶应力峰值为3.4 MPa；考虑徐变后，翘曲峰值为1.1 mm，板顶应力峰值为0.6 MPa，对应徐变松弛了翘曲和应力分别为82%、82%。

2)路面板不同位置，徐变应力松弛系数呈三维不均匀分布，徐变使最大应力位置发生改变。图12中，不考虑徐变时，板中位置的应力最大，而考虑徐变作用后，应力最大值位于板边中部，应力分布状态也发生了变化。应力松弛系数范围在65%～82%，也存在不均匀分布。

3)板角翘曲在温湿度荷载和徐变共同作用下，幅值周期波动衰减，60 d龄期内均为凹形翘曲形态。初期阶段，板顶为拉应力，板底为压应力，但随龄期增长，板顶应力表现为拉应力幅值降低、压应力幅值逐渐增加，出现拉压应力周期性波动，板底应力变化规律与板顶相反。

4)徐变作用效应显著性与时间的关系。以温度周期荷载作用下的一个波动周期内，路面板板顶和板底的“拉应力势能”(0.5个周期内的拉应力阴影面积S1)与“压应力势能”(0.5个周期内的压应力阴影面积S2)的差值进行比较判别。不同龄期拉压应力势能对比如表5，可以看出30 d龄期时两者相差15%以上，而到60 d龄期时两者相差6%，逐渐趋缓。

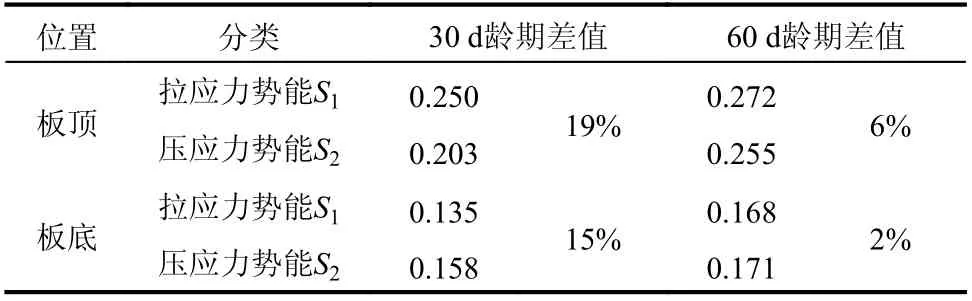
表5 不同龄期应力势能对比Table 5 comparison of t stress potential energy at different ages

5)应力和翘曲早龄期波动变化。

应力波动方面，仿真显示路面板仅在早龄期初期阶段会出现短暂的以拉应力或压应力为主的应力波动状态，在结构徐变持续作用30 d后，其内部各位置应力均为拉压循环应力，不存在始终为单纯的拉应力或压应力状态。

翘曲形态方面，仿真显示早龄期温湿度荷载与徐变持续作用30 d后，路面板结构会存在一个板角始终向上的凹形翘曲或是以凹形翘曲为主的翘曲形态，较少出现以凸形翘曲为主的形态，而不是平直状态。这与现场的监测试验结果一致[1,36]。

3.2 有约束路面板结构三维徐变效应

以单边约束、对边约束、三边约束和四边约束4种典型型式分析结构约束对路面板徐变效应的影响。温度荷载工况选择典型高温夏季早上施工，并洒水养护(前15 d龄期内暂未产生干缩)，图13给出了单边、对边、三边以及四边约束工况下板顶表面的应力松弛系数分布，图14给出了相应约束型式下考虑徐变后板顶表面的最大主应力云图。为对比路面板在四边无约束和四边约束条件下，徐变对翘曲与应力的影响，图15对比了前15 d龄期内的翘曲和应力时程曲线，图16给出了四边有、无约束时板顶表面应力松弛分布。图13、图14和图16中云图纵横坐标刻度与名称均与图12相同。

图13 不同约束型式下徐变松弛系数分布Fig.13 Distribution of creep relaxation coefficient under different constraint types

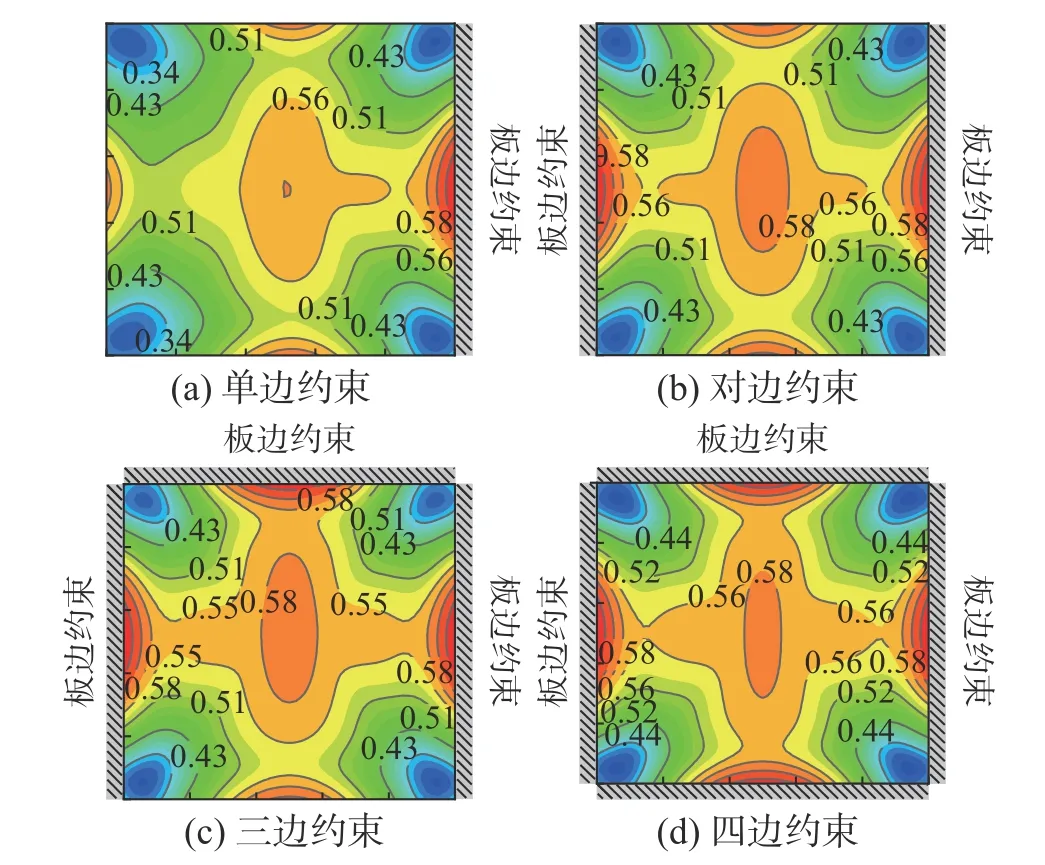
图14 板顶表面最大主应力云图/MPaFig.14 Cloud map of maximum principal stress on top surface

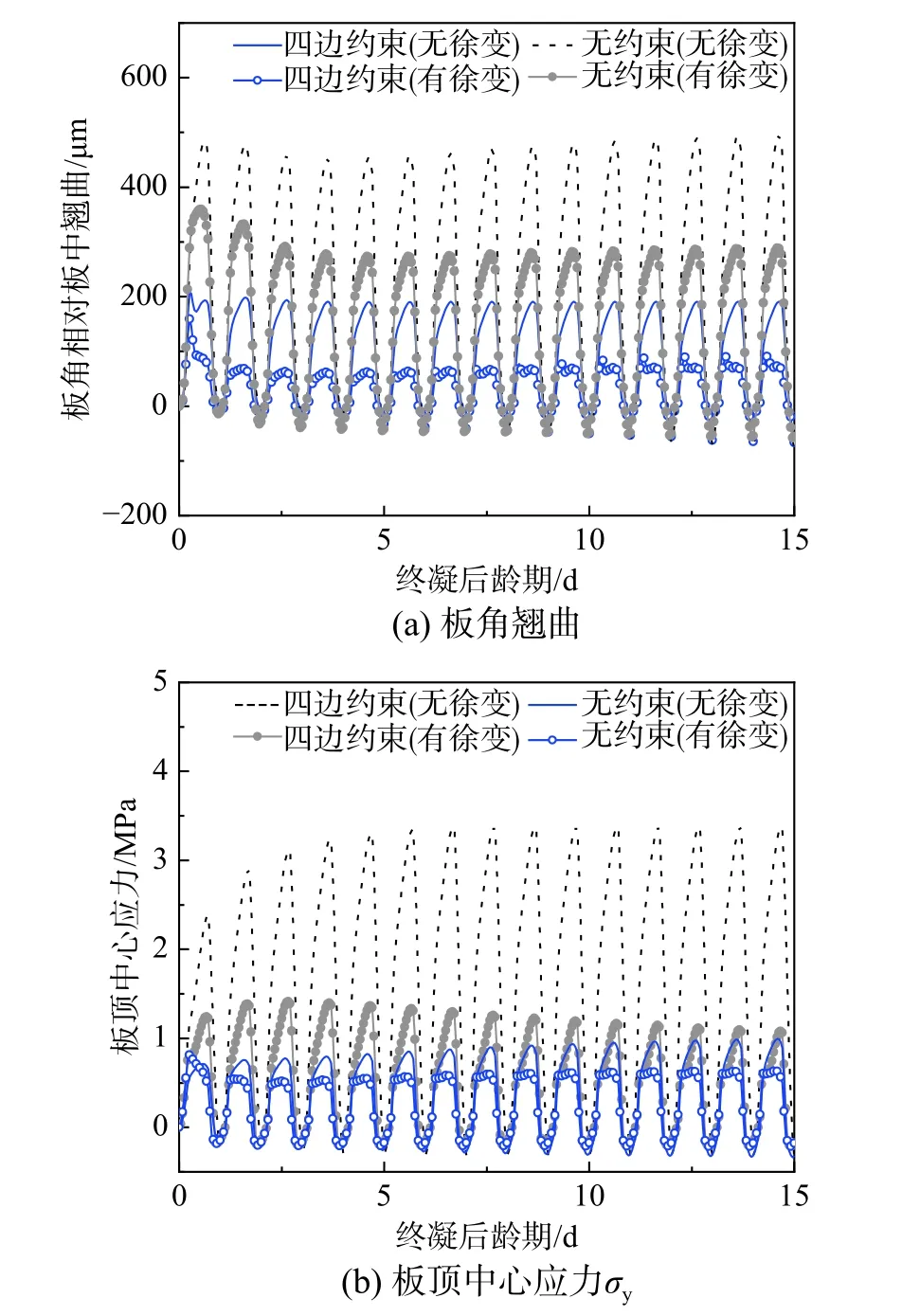
图15 有无约束条件下路面板早龄期翘曲与应力时程Fig.15 Curling and stress history of pavement slab with and without constraints

从图13～图16可以看出：

图16 有无约束下徐变对板顶应力的松弛系数分布Fig.16 Relaxation distribution of creep induced stress on slab top with and without constraints

1)板边不同约束型式显著影响徐变松弛效应分布，对应力松弛量级影响较小。不对称约束条件下，徐变松弛效应也呈不对称分布，应力最大松弛位置向受约束的板边靠近。如图13(a)和图13(c)单边和三边约束的路面板，特别是单边约束情况下，徐变松弛效应不对称分布更明显，应力最大松弛位置位于靠近受约束的右侧板边，而不是在板中心位置。板边对称约束条件下(对边与四边约束)，徐变松弛效应分布对称。应力松弛量级方面，单边、对边、三边、四边约束工况对应的最大松弛量分别为69%、69%、71%、71%，相差较小。此外，图13的云图中，四边约束工况下的红色区域面积显著大于单边约束工况，说明增加板边约束会提高路面板的徐变松弛效应。

2)徐变和板边约束共同影响下，路面板的最大应力位置位于受约束的板边中部，应力分布对称性与板边约束对称性一致。图14中，单边约束条件下，最大应力位置在右侧受约束板边的中部；双边约束工况下则位于左、右两侧板边中部，三边和四边约束工况亦是如此。

3)板边约束增加提高了徐变松弛效应量级、改变徐变松弛效应分布。图15中，四边自由的路面板，考虑徐变后翘曲和应力分别降低了42%、36%；而四边约束的路面板，考虑徐变后翘曲和应力分别降低了52%、66%。约束条件使徐变对路面翘曲和应力的松弛效应提高10%和30%。图16对比板边有无约束工况可以看出，四边无约束的自由板应力最大松弛位置集中在板中心，而四边有约束的路面板应力最大松弛位置向受约束的板边靠近。

4)结构约束对路面板徐变效应的综合影响有以下特点。路面板约束越大，对提高路面板早龄期徐变效应、降低路面板翘曲有利；但另一方面，有约束的路面板内应力总体上大于无约束的路面板。不对称结构约束会引起不对称翘曲变形和应力，徐变效应也会对应约束情况而改变。同时，无论是板边无约束还是板边有不同型式的约束，徐变均造成了路面板早龄期最大初应力位置发生改变，最大初应力位置从不考虑徐变的板中位置转移至板边中部，建议路面破坏模式分析时，综合考虑徐变效应对应力量级和最大应力位置的影响。

3.3 温度条件对路面板徐变效应的影响

选取不同的整体平均温度条件、施加相同的温度梯度差(图9)，并与未考虑温度影响的GKM徐变模型的仿真结果进行对比，分析温度条件对路面板徐变效应的影响。图17给出了徐变对路面板早龄期翘曲和应力的影响，由于早期徐变显著，图中显示终凝后前48 h的翘曲和应力变化。

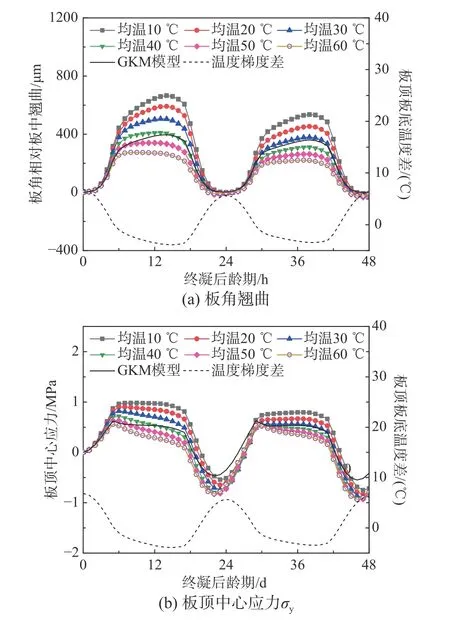
图17 不同温度下徐变对早龄期应力和翘曲的影响Fig.17 Effect of creep on stress and curling in early age under different temperatures

从图17可以看出：随着温度的升高，早龄期混凝土徐变作用显著增大，路面板应力和翘曲量级显著降低。混凝土平均温度10 ℃工况，板顶中心最大应力为0.98 MPa，板角翘曲幅值为665 µm，而平均温度60 ℃工况，板底中心最大应力仅为0.57 MPa，板角翘曲幅值为275 µm，同比降低了42%和58%。

分析可以发现，温度对路面板早龄期行为的影响有2个角度：一个角度是高温条件下不利的温度梯度和湿度梯度会引起面板翘曲和应力；但从影响徐变的另一个角度，高温条件增加了徐变的松弛作用，忽略温度对徐变影响将低估高温、高估低温条件下的徐变效应，进而高估了高温和低估了低温条件下路面板的早龄期翘曲和应力。

3.4 湿度条件对路面板徐变效应的影响

为了对比分析早期不同养护时长造成的湿度条件变化对路面板徐变效应的影响，养护时长选择1 d、3 d和7 d，认为养护结束后产生湿度梯度差，温湿度荷载大小如图9所示，其中加载湿度梯度差的时间点分别为终凝后1 d、3 d、7 d。图18显示了不同养护时长工况下，徐变对路面板前28 d内的翘曲和应力影响情况，图19对比了1 d和7 d养护时间下板顶表面徐变松弛分布，图19云图纵横坐标刻度和名称与图12相同。

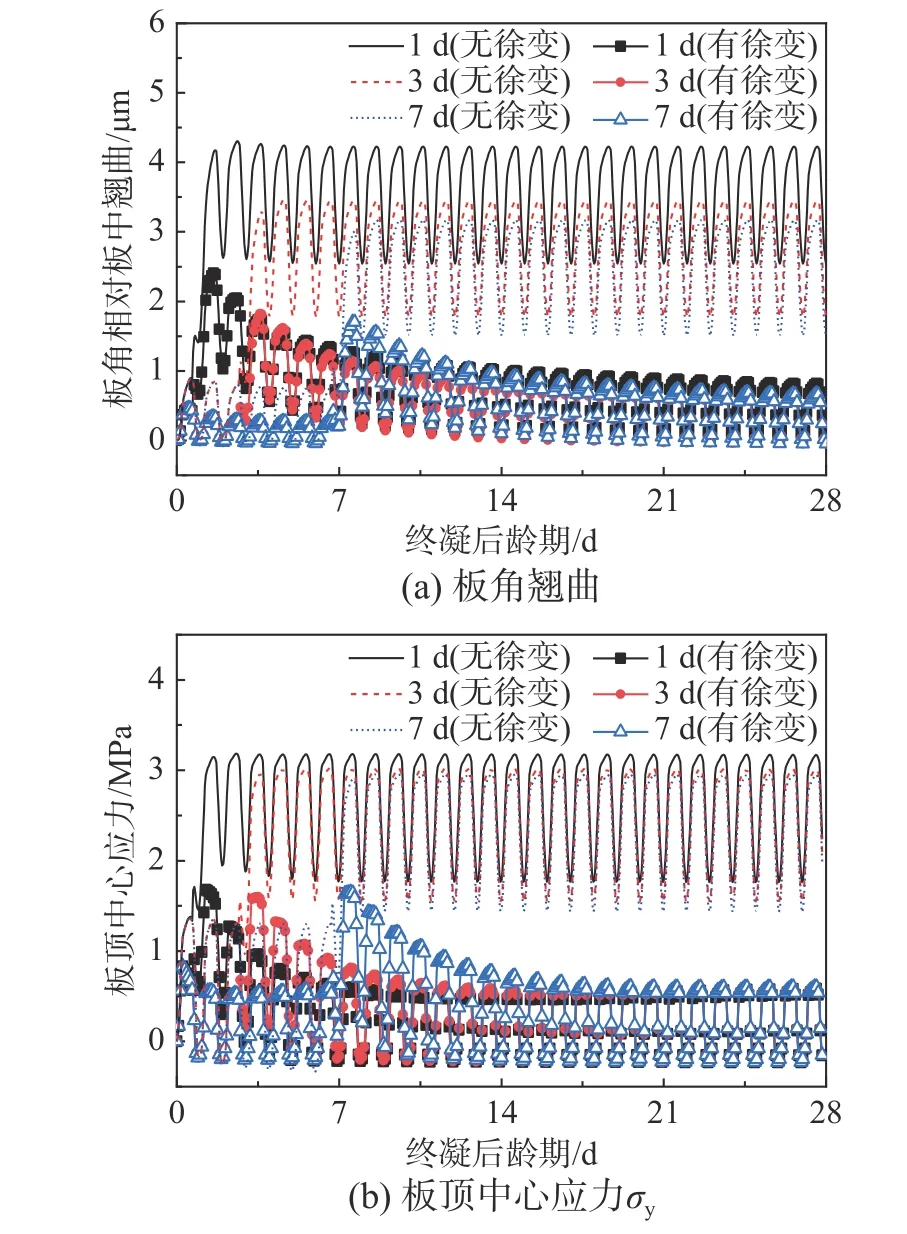
图18 不同养护龄期对应的路面板翘曲和应力时程Fig.18 Curling and stress history of pavement corresponding to different curing ages

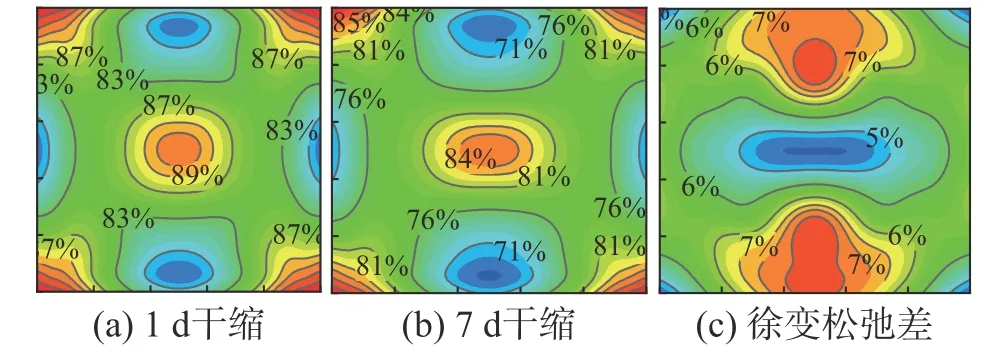
图19 不同养护龄期下徐变对板顶应力的松弛系数分布Fig.19 Relaxation distribution of creep induced stress on slab top under different curing ages

从图18和图19可以看出：不同龄期产生湿度干缩对路面板早龄期翘曲和应力以及徐变效应均有一定的影响。干缩龄期越早，路面板的徐变效应越明显。1 d、3 d和7 d干缩龄期情况下，28 d龄期后，徐变降低板中应力峰值分别为89%、86%和84%，降低板角翘曲峰值分别为86%、83%和81%。说明干缩龄期越早，徐变对路面板的应力峰值和翘曲峰值的松弛效应约显著。从第28 d板顶表面的徐变松弛量分布来看，1 d干缩龄期工况下应力松弛比例在75%以上，而7 d干缩龄期工况下应力松弛比例在66%以上，两者相差约9%。从云图分布来看，干缩龄期对徐变效应的分布特性影响较小。

3.5 材料参数对路面板徐变效应的影响

考虑到保证道面的耐磨性，我国路面混凝土基本都是采用干硬性混凝土配合比设计，混凝土石子用量、水泥用量、砂率、水灰比等参数调整范围小，基于已有研究对各材料因素对混凝土徐变影响敏感性的研究结果发现，敏感性从高到低依次是水灰比、水泥用量、减水剂、骨料性状[37]。选取水灰比作为代表参数，对比不同水灰比对路面板徐变效应的影响，图20给出了水灰比为0.40和0.46时路面板早龄期徐变松弛系数分布云图，图20云图纵横坐标刻度和名称与图12相同。从图20可以看出，水灰比提高，路面板应力徐变效应增加。水灰比为0.40、0.46情况下，板顶中心应力分别松弛47%和55%，整体上，徐变对路面早龄期松弛效应提高8%以上，徐变应力松弛分布云图没有明显改变。

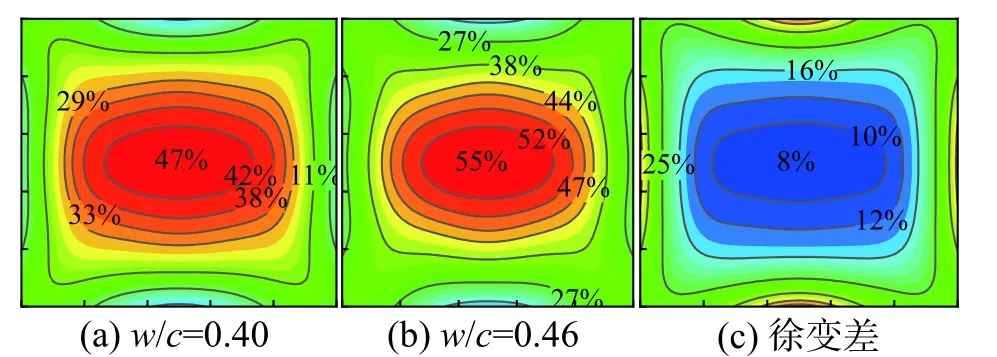
图20 不同水灰比下徐变对板顶应力的松弛系数分布Fig.20 Relaxation distribution of creep induced stress on slab top under different water cement ratios

值得注意的是，实际路面工程中混凝土很少情况下水灰比达到0.46，大多数在0.38～0.40之间，这间接说明道面混凝土配合比改变对路面板徐变效应影响较小，路面混凝土材料徐变相比泵送混凝土要小。在材料方面适当降低水泥的强度增长速度对于增加大徐变有利。

4 敏感性分析

为系统对比结构、材料、施工参数对路面板结构徐变效应影响的敏感性，基于建立的三维路面板早龄期数值仿真程序，分两个角度进行分析：1)徐变参数和其他参数对板早龄期变形和应力的影响敏感性比较；2)各参数对60 d龄期时徐变松弛效应的影响敏感性比较。

4.1 路面板早龄期徐变效应影响敏感性

敏感性观测对象为第60 d的板角翘曲峰值和板顶中心处应力峰值，表6和图21给出了主要参数以及敏感性等级，其中对路面板翘曲或应力的影响超过40%的参数为Ⅰ级，参数影响性最为显著，影响在20%～40%的参数为Ⅱ级，影响在20%以下的参数为Ⅲ级，影响性较低。

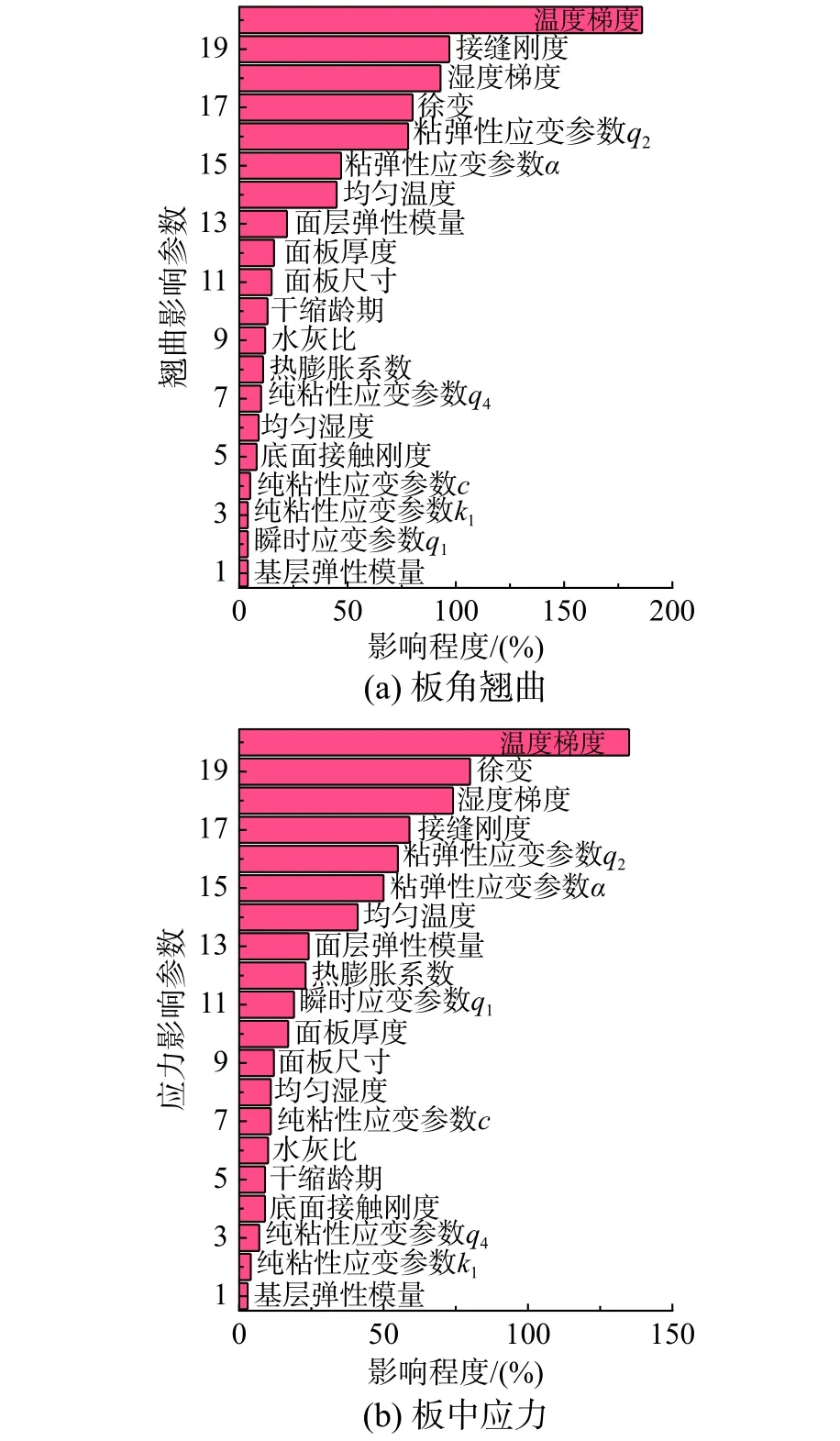
图21 参数对路面板早龄期翘曲和应力的影响敏感性Fig.21 Effect sensitivity of parameters on early-age curling and stress of pavement slab

表6 路面早龄期性状参数敏感性分析结果Table 6 Parameter sensitivity analysis results of pavement early-age curling and stress

敏感性分析结果显示，徐变(含模型参数q2、α)对路面板早龄期翘曲和应力的影响量级与温湿度荷载、接缝约束的影响量级相当，影响最为显著；整体温度，面层混凝土模量和热膨胀系数次之；面板尺寸，板厚，干缩龄期，水灰比，徐变参数q1、q4、c、k1，基层模量以及底面约束等影响较低。

对徐变模型参数的敏感性分析可以用来判断各参数对徐变作用的贡献程度，可以看出，代表水化固化产物粘弹性质的徐变参数q2、α影响显著，说明粘弹性应变在徐变性质中起主导作用，与水灰比、水泥类型、强度等材料参数有关。

各参数中，温湿度梯度、面层混凝土模量、热膨胀系数、干缩龄期、面板尺寸、板厚和基层模量与路面板翘曲和应力正向相关；徐变、水灰比、整体温湿度条件与路面板翘曲和应力为负向相关；接缝约束和底面约束与路面板翘曲为负相关，而与路面板应力是正向相关的。

4.2 路面板早龄期徐变效应的参数影响敏感性

对路面板早龄期徐变效应的影响敏感性进行分析。参数与取值范围见表7，以参数对60 d龄期时徐变效应的改变范围作为敏感性评价指标。在各参数取值范围内，对路面板板顶中心应力峰值的徐变松弛量级改变超过20%的参数为Ⅰ级，影响性最为显著，板顶中心应力峰值徐变松弛改变量级在10%～20%、低于10%的参数分布为Ⅱ、Ⅲ级，影响敏感性分析结果见表7和图22。

从表7和图22可以看出，徐变参数q2、温度梯度、板边约束、湿度梯度、整体温度条件和面板尺寸对路面板徐变效应的改变量在20%以上，影响最为显著；徐变参数q1及α、干缩龄期、面层弹性模量、热膨胀系数以及混凝土水灰比的影响在10%～20%，影响次之；整体湿度条件、底部约束、面板厚度、基层弹性模量以及徐变参数q4、c、k1对路面板徐变效应的影响最低。

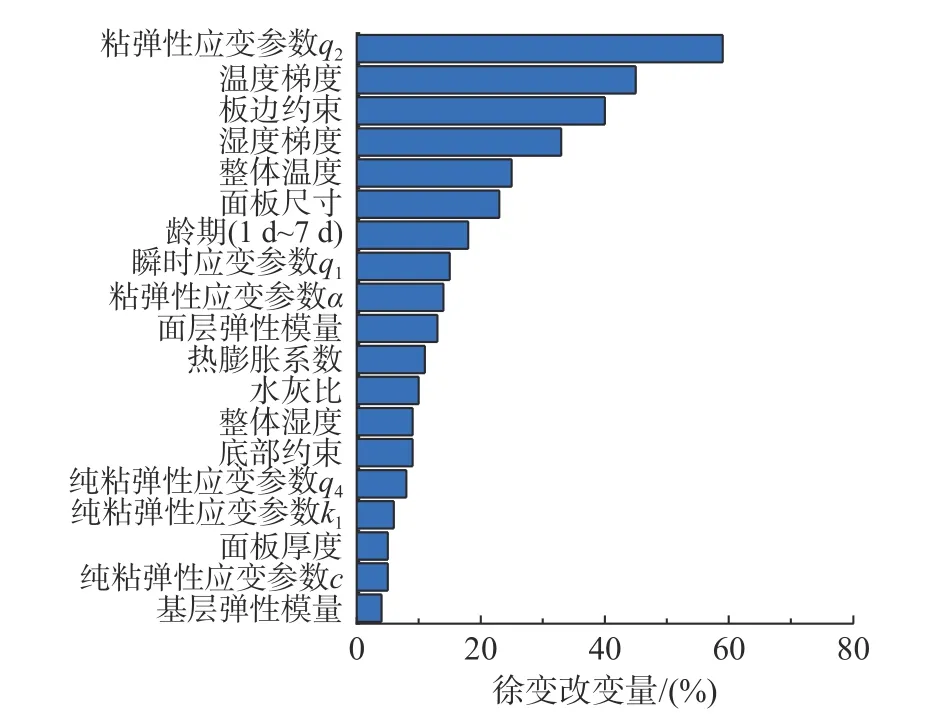
图22 主要因素对路面板徐变效应的影响Fig.22 Influence of main factors on creep effect of slab

表7 路面徐变效应参数敏感性分析结果Table 7 Parameter sensitivity analysis results of pavement early-age curling and stress

5 比较与讨论

5.1 理论与现场试验比较

为了解本文程序对实际路面工况的模拟效果，选取胡昌斌等[25]在福建漳州省道208开展现场足尺板竖向位移实测结果及其数值仿真结果进行对比。路面板结构尺寸、材料参数以及温湿度条件等数据资料见文献[25]，混凝土水灰比为0.40，徐变参数见表2。板角竖向位移对比结果见图23。

由图23可以看到，翘曲峰值模拟方面，文献[25]模拟板角翘曲峰值与实测翘曲峰值误差在50%以上，特别是在第5 d龄期内，文献[25]翘曲峰值计算值约为翘曲实测值的3倍。而本文程序得到的板角翘曲峰值与实测翘曲峰值误差仅为10%左右。在计算值与实测值的平均误差方面，文献[25]的计算结果与实测值的平均误差为6.90 µm，本文为5.07 µm，模拟精度提高了26.5%。

图23 板角竖向位移校核Fig.23 Verification of vertical displacement of slab corner

5.2 理论研究比较与工程建议

本文研究与以往理论研究进行比较，具体比较对比的理论见表8。

表8 路面板徐变效应已有分析理论Table 8 Analysis theory of pavement creep effects

理论对比显示：

1)路面板徐变效应量级方面，以往分析理论和本文研究均表明徐变降低了路面板的翘曲和应力，对比分析理论①～⑦发现，徐变松弛温度应力或湿度应力峰值在29%～66%，本文考虑结构、环境、材料等因素影响后发现，徐变的应力松弛系数在40%～90%，有了明显增大。分析认为分析理论①、③～⑥单独关注温度荷载或湿度荷载，可能低估了不利的温度梯度和湿度梯度作用；同时分析理论①～⑦未考虑高温条件、板边约束对徐变效应的影响。

2)本文考虑了三维结构的徐变效应，发现徐变松弛效应在空间上分布不均匀，板边约束型式显著影响徐变松弛分布的对称性，使应力最大松弛位置向受约束的板边转移。通过应力时程曲线循环波动周期内的“拉应力势能”与“压应力势能”之间的比例差小于5%进行观察，宜选择60 d作为分析徐变影响效应的时间。

3)综合以上可以认识到，徐变对路面板早龄期翘曲和应力有显著的松弛效应，可充分利用徐变的松弛效应降低早龄期性状对路面板的不利影响。从敏感性结果来看，徐变与结构约束共同作用的影响最为显著，板边约束分布可以调控路面板应力最不利位置，使路面板翘曲和应力分布更为均匀。

4)可以从提高徐变效应降低路面板早龄期初始翘曲与初始应力角度，提高路面性能，结构方面可适当考虑增加路面板四周接缝约束刚度，提高徐变的早龄期松弛效应，可显著降低路面板的不利翘曲变形；材料方面采用低热缓凝水泥等适当降低水泥的强度增长速度，对徐变有利，使徐变充分松弛路面板早龄期应力；施工方面采用水凝胶养生剂养生法逐级降低湿度，充分利用面板昼夜周期环境温度诱发的循环变形和早龄期高徐变作用，降低初始永久变形，提高道面平整度。

6 结论

基于微预应力-固结理论的徐变模型，综合考虑材料、结构以及环境对徐变的影响，建立三维水泥混凝土路面板早龄期力学行为仿真程序，揭示了路面板三维徐变效应机制和工程参数对路面板徐变效应的影响特性，并与已有理论进行了比较，研究表明：

(1)徐变对路面板的作用是一种松弛效应，显著降低了早龄期翘曲和应力，其对翘曲和应力的影响量级与温湿度梯度、结构约束的影响量级相当，最为显著；徐变效应也受到温湿度梯度、板边约束和整体温度等因素的显著影响。

(2)徐变、水灰比、整体温度与路面板翘曲和应力负向相关；温湿度梯度、混凝土模量、热膨胀系数、面板尺寸、板厚、基层模量与路面板翘曲和应力正向相关；接缝约束和底面约束与路面板翘曲为负相关，而与应力正向相关。

(3)徐变松弛效应在空间上分布不均匀，板边约束型式显著影响徐变松弛分布的对称性，应力最大松弛位置向受约束的板边中部靠近；路面板徐变松弛效应有显著经时特性，前7 d早期徐变效应最为显著，60 d后趋于稳定；温度梯度与整体温度提高，徐变松弛效应显著增加。

(4)理论比较显示，忽略温、湿度对徐变的影响会低估高温、高估低温条件下的徐变效应，考虑三维结构徐变效应，可获得更全面的路面板力学计算初始基准值，工程中可基于徐变效应设计降低路面板早龄期初始翘曲与初始应力，提高路面性能。