基于MATLAB软件平台的局放信号波形分析
蒋池剑 余祖良 郑智勇




摘 要:局部放电是引起电力设备绝缘缺陷的主要因素,准确检测局部放电信号对于提高电气设备的可靠性至关重要。然而,局部放电信号中往往夹杂着大量噪声,严重影响判断。鉴于此,采用MATLAB软件编程,利用希尔伯特-黄变换算法,通过主体函数EMD(y),实现对局部放电真实信号的提取。实例检测结果表明,该方法具有一定的有效性和可靠性。
关键词:希尔伯特-黄变换;MATLAB软件;局部放电;信号提取
中图分类号:TM93 文献标志码:A 文章编号:1671-0797(2022)07-0042-04
DOI:10.19514/j.cnki.cn32-1628/tm.2022.07.011
0 引言
局部放电现象多出现于高压电气设备中,这种放电会造成导体间的绝缘局部短接,加速电气设备绝缘介质的老化和损坏,从而缩短设备的使用寿命,严重时还会引发绝缘击穿,损坏设备,造成人员生命、财产损失。然而,局放放电量小,发热不明显,很难对其识别和判断。当局放现象明显时,局放的发热量往往已经造成一定的绝缘材料损失。
局部放电是电力变压器中绝缘缺陷的主要特征之一,且由于变压器在电力系统中的重要地位,准确检测局部放电成为延长变压器使用寿命、提高电力系统稳定性的重要措施。目前,国内外采用的局部放电识别方法主要有超声波法、电气法和超高频法等。这些方法各有千秋,但正确应用的前提都是提取出局部放电的信号。然而,局部放电信号中往往夹杂着大量无关噪声,严重影响判断[1]。对此,1998年,中国台湾海洋学家黄锷在希尔伯特变换的基础上提出了希尔伯特-黄变换[2],依靠这种变换方法可以较为方便准确地提取和分离故障信号、干扰信号。黄锷教授在完成对希尔伯特-黄变换的研究后,上传了其变换的程序包,但程序包难以解码,内部程序不可见,对于其他学者而言难以进行进一步的优化,故本文尝试独立于该程序包,利用MATLAB撰写希尔伯特-黄内核变换代码,并利用其对局放波形进行分析和研究。
1 希尔伯特-黄变换算法
希尔伯特-黄变换(HHT)算法是由中国台湾海洋学家黄锷于1998年提出的,其基于希尔伯特变换并有所改进。该方法分为经验模态分解(EMD)和希尔伯特谱分析(HSA)[3-4],其处理信号的方式为:先对该信号进行经验模态分解,分解出符合一定条件的模态因子(IMF),然后对所有模态因子进行希尔伯特谱分析,得到相应的希尔伯特谱,最终将所有的希尔伯特谱汇总,便能得到原始信号的希尔伯特谱。
HHT会对原始信号y(t)进行检测,若其不单调,便对其进行经验模态分解。其主要步骤为,首先绘出该信号的上下包络线bs和bx,然后计算包络线的均值j1:
j1=(1)
随后用原信号减去均值,得到一个新的信号y11(t)。
y11(t)=y(t)-j1(2)
对得到的y11(t)进行检测,检测条件如下:(1)信号的极值点数和信号的零点数相差不超过1;(2)信号的上下包络线的局部均值为0。若其不满足以上条件,重复m次上述步骤,直到其满足以上条件。得到满足条件的信号y1m(t),其被称为模态因子IMF。得到一个IMF后,令y1m(t)=r1(t)并记录,然后用原信号减去该IMF,所得的残余信号称为c1(t)。若c1(t)仍不单调,则再次对其进行EMD分解,直到满足IMF条件并得到新的ri(t)和残余信号ci(t)。重复该步骤n次,直至分解出的cn(t)单调,并得到n个ri(t)和一个单调信号cn(t),该单调信号被称为残余信号。至此,原信号被分解为n个IMF和一个残余信号,即:
y(t)=ri(t)+cn(t)(3)
再將这n+1个信号进行希尔伯特变化,得到瞬时频率、瞬时能量、信号谱等,将所得的结果输出,即完成信号的分解。
其核心为EMD处理。从频域上来看,是高频逐渐到低频;从时域上来看,其特征时间尺度逐渐扩大。同时,在某些情况下,为了防止过度分解,往往需对其设置一个尺度,该尺度称为SD,如式(4)所示:
SD=(4)
一旦计算出的SD小于某个阈值,则认为该次分解已经足够小,并立即结束该次EMD计算。一般将阈值设置为0.2~0.3。
2 希尔伯特-黄变换的代码实现
了解了希尔伯特-黄变换的原理后,采用MATLAB编程实现这一变换。其主体函数如下EMD(y)所示,y是输入信号。实现希尔伯特-黄变换的重点和难点在于如何实现EMD变换。
function a = EMD(y)
while ~dangdiao(y)
y1=y
sd=Inf
while (sd > 0.1) | ~imf(y1)
s1 = getspline(y1);
s2 = -getspline(-y1)
h = y1-(s1+s2)/2
sd = sum((y1-h).^2)/sum(y1.^2)
y1=h
end
a{end+1} = y1
y=y-y1
end
end
在EMD(y)函数中包括3个副函数,函数名分别为“dangdiao” “imf” “getspline”。其中函数“dangdiao”用来判断输入信号是否为单调函数,若不为单调函数则进行循环;函数“imf”用来判断信号是否满足IMF条件,若不满足则继续循环;函数“getspline”为绘制上下包络线函数。而sd作为限制尺度,用于防止过度分解。
函數“dangdiao”用以判断信号在一定区间内是否为常数,其代码如下:
function u=dangdiao(y)
u1 = jizhidian(y);
if u1 > 0
u = 1;
else
u = 0;
end
end
函数“jizhidian”为极值检测函数,能够测量出原始信号的单调方式。若原始信号既有单调增区间,又有单调减区间,则返回值为0;除此之外,返回值为1。
function n=jizhidian(y)
k=find(diff(y)>0)
m=find(diff(y)<0)
k1=size(k)
m1=size(m)
if m1==0 | k1==0
n=1
else
n=0
end
end
函数“imf”函数的原理是测量原始信号的零点和极点的数量。若零点和极点的数量相差超过1,则不满足IMF条件,返回值为1,否则返回值为0。其中,“peaks”函数作用为寻找信号全部的极值点,其将信号求二阶导,若一阶导值大于0,而二阶导值小于0,则其必是极大值点。由此寻找出信号全部的极值点。
function u=imf(y)
N=length(y)
u1=sum(y(1:N-1).*y(2:N) < 0)
u2=length(peaks(y))+length(peaks(-y));
if abs(u1-u2)>1
u=0
else
u=1
end
end
函数“getspline”基于“spline”函数进行包络线的绘制。“spline”是一个较为复杂的函数,其能从输入数据中寻找内在联系,并以此绘制出包络线。
function s=getspline(y)
N1=length(y);
p=peaks(y);
s=spline([0 p N1+1],[0 y(p) 0],1:N1);
end
运行上述代码,就可以实行信号分析,提取出原始信号的主体部分、次要信号以及噪声信号。
3 二维希尔伯特-黄变换的代码实现
与一维信号EMD变换不同,BEMD变换主要面向二维图片或波形,其处理流程与EMD变换类似,但增加了信号识别和信号特征提取,具体处理流程如图1所示。
BEMD变换代码实现函数主要由三部分组成:主体函数、包络线绘制函数和单调判断函数。其主体函数用于储存分离出的IMF和余项;而包络线绘制函数通过对函数进行描点处理,寻找其极值点,并以此绘制包络线;同样,单调判断函数也通过对函数的描点处理,判断其是否单调。其代码如下:
clear all
img=imread('wave.jpg')
[r,c,d] = size(img);
if d ~= 1
img = im2double(rgb2gray(img));
else
img = im2double(img);
end
imshow(img)
k=1;
m=0;
input_img=img;
A={}
while(~dangdiao(input_img))
[imf_de res_de]=baoluoxian(input_img);
A{k}=imf_de;
input_img=res_de;
k=k+1
end
A{k}=res_de;
function [imf_de res_de]=baoluoxian(input_img)
[width height]=size(input_img);
x=1:width;
y=1:height;
input_img_temple=input_img;
SD=Inf
while(1)
[zmax imax zmin imin]=extrema2(input_img_temple);
[xmax ymax]=ind2sub(size(input_img_temple),imax);
[xmin ymin]=ind2sub(size(input_img_temple),imin);
if SD<0.2
break
else
[zbs,~,~]=gridfit(ymax,xmax,zmax,y,x);
[zbx,~,~]=gridfit(ymin,xmin,zmin,y,x);
zbav=(zbs+zbx)./2
imf_de=input_img_temple-zbav;
SD=sum(sum(imf_de-input_img_temple).^2)/sum(sum(imf_de).^2);
input_img_temple=imf_de;
end
res_de=input_img-imf_de;
end
end
function m=dangdiao(input_img)
[zmax imax zmin imin]=extrema2(input_img);
[xmax ymax]=ind2sub(size(input_img),imax);
[xmin ymin]=ind2sub(size(input_img),imin);
xx=size(xmax,1)
xn=size(xmin,1)
u1=xx*xn
if u1>0
m=0
else
m=1
end
end
4 实例测试
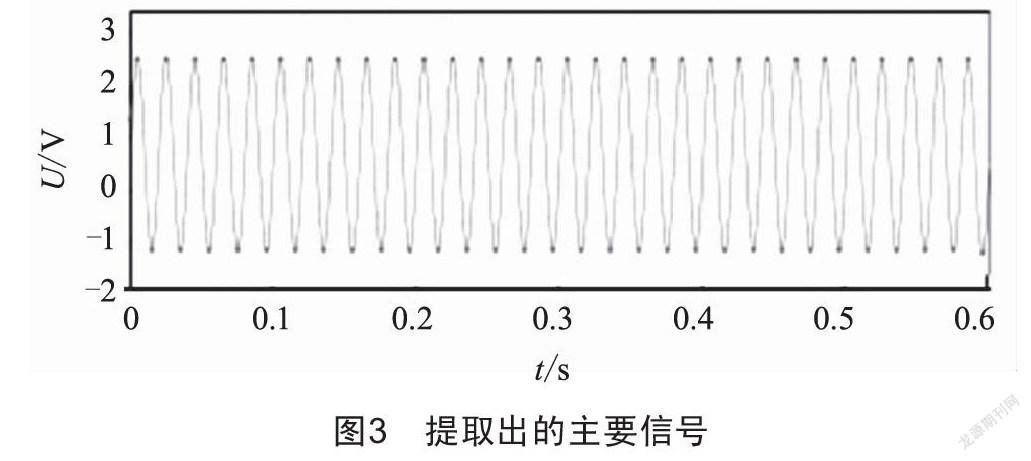
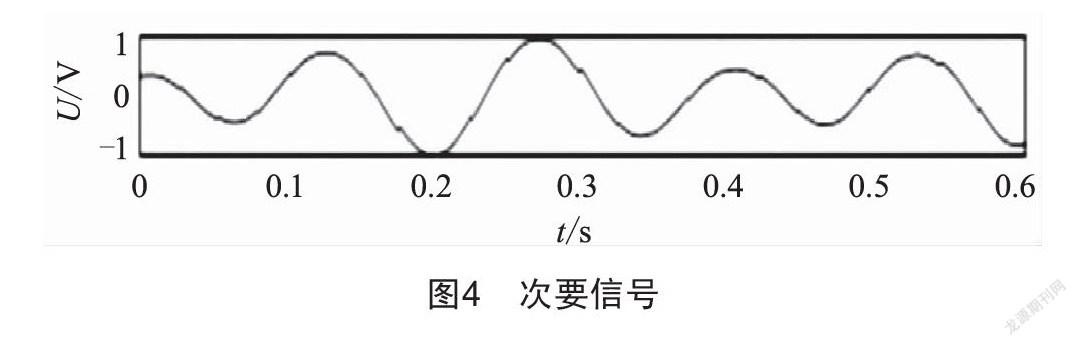
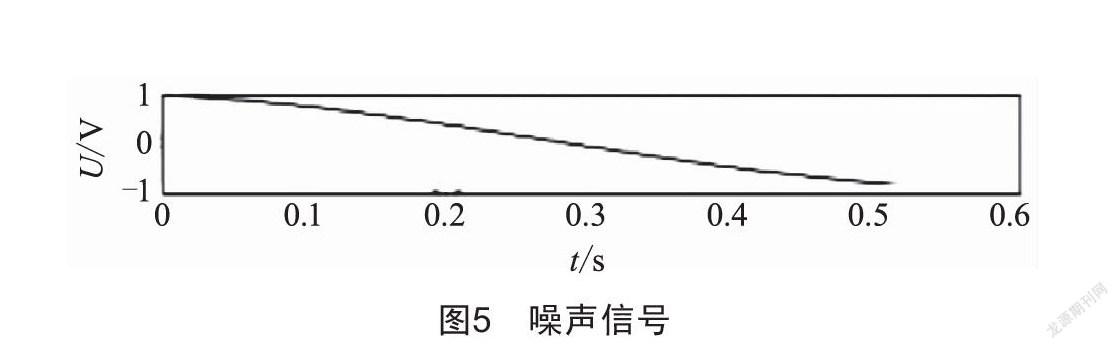
图2为某变电站10 kV开关柜的局部放电信号波形图,采用本文方法利用MATLAB对其进行信号提取和分解,得到的真实信号如图3所示,次要信号如图4所示,噪声信号如图5所示。本文方法能很好地将真实信号从原始信号中剥离出来。
5 结语
本文研究了HHT的变换方式,利用MATLAB软件代码逐步实现了该变换,并取得了一定的成果。相比于简单的希尔伯特变换,希尔伯特-黄变换增加了EMD处理,能够更好地处理非线性复杂信号,且相较于常用的傅里叶变化和小波变换,其拥有较强的自适应性,泛用性更好。在出现奇异信号(不规则信号)时,主要采用积分分解法的傅里叶变化和小波变换会出现巨大的计算量,且容易产生虚假信号,严重影响判断;而希尔伯特-黄变换能够很好地处理奇异信号。
[参考文献]
[1] 罗新,牛海清,宋廷汉,等.基于S变换和概率神經网络的局部放电特征提取及放电识别方法[J].南方电网技术,2020,14(7):17-23.
[2] 李光辉.基于希尔伯特黄变换及其改进方法的信号分析研究与应用[D].成都:成都理工大学,2012.
[3] 曾祥,周晓军,杨辰龙,等.基于经验模态分解和S变换的缺陷超声回波检测方法[J].农业机械学报,2016,47(11):414-420.
[4] 邬蒙蒙,周怀来,林萍,等.改进的完备经验模态分解和广义S变换相结合的地震信号衰减分析[J].地球物理学进展,2020,35(5):2001-2008.
收稿日期:2022-01-11
作者简介:蒋池剑(1978—),男,浙江人,高级工程师,研究方向:抽水蓄能电站生产管理。
通信作者:郑智勇(1978—),男,湖南人,工程师,从事电气设备管理工作。

