高速矩形水舌表面破碎的大涡模拟

吴 鹏，张 华

(华北电力大学水利与水电工程学院，北京 102206)

坝身泄洪孔或泄洪洞泄洪时的挑流水舌会发生雾化现象，其雾源有三个部分，分别是水舌扩散掺气、水舌入水喷溅、水舌空中相碰而产生的雾化[1- 5]。其中第一雾源主要来自水舌表面破碎，虽然其雾源量较小，但第一雾源的特性与第二、第三雾源的特性密切相关，并且是第二与第三雾源的基础。因此，高速矩形水舌的表面破碎机理是一个重要的科学问题。

对于水舌表面初次破碎机理这个问题，可追溯到小尺度自由射流的研究，对其的研究已取得如下的研究进展。施红辉等人推广了Ryhming模型，确定了喷嘴内部结构对脉冲喷流特性的影响[6]。金晗辉等人对三维小宽高比矩形喷嘴射流流场进行了数值研究，着重分析了流场中各典型截面上流场速度的分布特点、脉动速度分量的特征[7]。Abbas等人重点研究了主动与被动扰动同时作用下喷流的时空动力学[8]。Jaberi等人通过理论和实验研究了矩形和椭圆液体射流的轴变换现象的振荡波长和频率[9]。Zhang等人通过实验发现了受外部扰动的矩形喷嘴喷射出的微喷流的破裂特性[10]。李子丰等人使用OpenFOAM中的VOF-LPT耦合算法模拟了射流雾化过程，为更大尺度的模拟射流提供了可行的高效模拟方案[11]。

但在这些研究中，大部分忽略了重力因素或其影响微乎其微，而重力对于挑流雾化的大尺度水舌表面破碎的影响不可忽略。除了重力因素，涡结构也是最主要的影响因素之一。刘宣烈认为，入口处由于流速脉动等因素，使水舌围绕其运动迹线摆动，促使涡产生，加剧涡之间的相互作用，加速了水舌的破碎[12]。吴持恭综合了表面波破碎理论、边界层发展理论以及紊动强度理论，认为水流内部不同尺度的涡体是导致水舌表面初次破碎的主要原因之一[13]。

为研究高速矩形水舌的初次破碎，采用流体体积法与大涡模拟法对其进行数值模拟计算。速度边界使用涡流法，在入口处加入随机点涡阵，凸显随机点涡阵作用条件下，矩形水舌的破碎和雾化特性。为进一步研究挑流水舌的后续破碎、雾化奠定基础。

1 数学模型

1.1 基本假定

(1)水舌为不可压缩性流体；

(2)不计初始风场速度。

1.2 水舌运动基本方程

研究水舌在气相环境下的运动，满足如下连续性方程：

(1)

动量方程：

(2)

式中，ui—速度张量，m/s；ρ—密度，kg/m3；p—压强，Pa；ν—运动粘度，m2/s；fi—单位质量力，m/s2。

1.3 体积分数法与液滴转换模型

流体体积的相方程为

(3)

式中,α—相体积分数。

为统计与分析破碎后液滴的分布，采用流体体积法-离散颗粒法的液滴转换模型[14]。该方法结合了欧拉-欧拉法的VOF(Volume of Fluid)模型和欧拉-拉格朗日的DPM(Discrete Phase Model)模型，如果液体块满足设置条件，即当其体积小于体积标准或其球形度大于球形度标准时，则将其转化为离散的液滴粒子，然后将这些粒子从连续相的欧拉体系中转移到离散相的拉格朗体系中。该模型常用于模拟燃气轮机、内燃机和其他类似应用中的液体雾化[15]。

(4)

式中,Q—球形度；Vp—液体块体积，m3；Sp—液体块表面积，m2。

1.4 大涡模拟模型

(5)

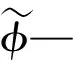
过滤操作后产生的亚格子模型主要捕捉小尺度涡，其亚格子尺度应力τij为

(6)

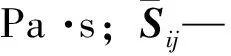
因为挑流水舌在射出时会产生涡结构，所以采用LES中的WMLES(Algebraic Wall-Modeled LES)模型[16]，其允许在高雷诺数下计算壁面有界流动，而无需像传统LES那样在高雷诺数下大幅提高网格分辨率。同时选择WMLES中的S-Ω模型，该模型提供零涡流粘度，可以计算转捩效应，在分裂计算层计算中不会产生过大的涡流粘度[17]。其亚格子尺度的涡流粘度μt为

(7)

式中,κ—von Kármán常数，取值为0.4187；CSmag—Smagorinsky常数，取值为0.2；dw—离固壁的垂直距离，m；Δ—修改后的网格比例尺；y+—垂直于固壁的内部比例；S—应变率。

1.5 速度边界条件

挑流水舌在通过泄洪孔或泄洪洞射出的这个过程中，由于墙体与水流的相互作用，会产生强烈的扰动效果，导致在进入自由气相时，涡结构其实已经存在，在后续的水舌破碎中发挥重要作用。所以该模型的速度边界采用涡流法速度边界，如图1所示，在入口截面上给予随机分布的点涡[18]。

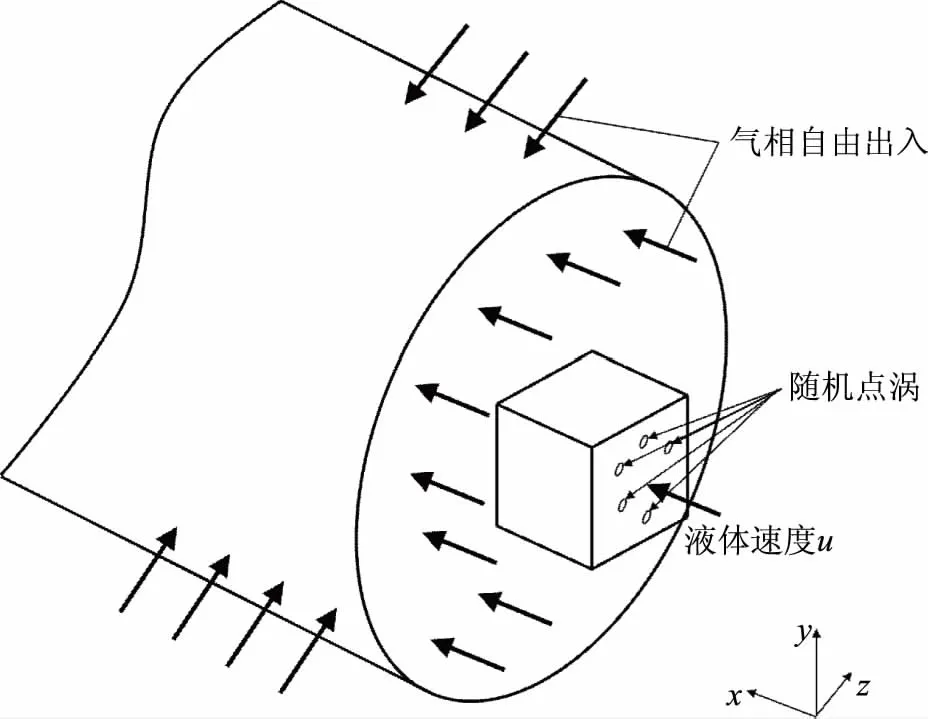
图1 随机点涡位置示意图

通过扰动涡度场(即垂直于流向方向的平面上的二维平面)在指定的平均速度剖面上添加扰动，该涡旋法是基于涡旋量的二维演化方程的拉格朗日形式和毕奥-萨伐尔定律[19]。

(8)

(9)

式中,ω—涡量大小，s-1；x—位置向量；xi—点涡的位置向量；η—涡旋点的空间分布；Гi—速度环量，m2/s；A—入口截面面积，m2；k—湍流动能，m2/s2；N—涡旋点的数量。

将这个随机点涡阵的扰动速度场速度离散化后

(10)

(11)

式中,z—流向方向的单位向量;σ—涡旋点的大小，m；ε—平均湍流耗散率，m2/s3。

故瞬时速度为

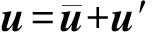
(12)

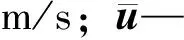
在水舌入口边界上，将随机点涡阵所诱导的扰动速度，添加到指定的平均速度上，以实现涡结构对水舌速度边界条件的影响。

2 水舌数值模型的计算

2.1 网格划分与计算条件

基于有限体积法，采用对矩形水舌与空气初始交界面加密后的蝶形网格，如图2(a)所示，矩形入口为0.01m×0.01m，这种网格可以更好地刻画水舌表面的发展变化，易于获得重点关注区域的数据。

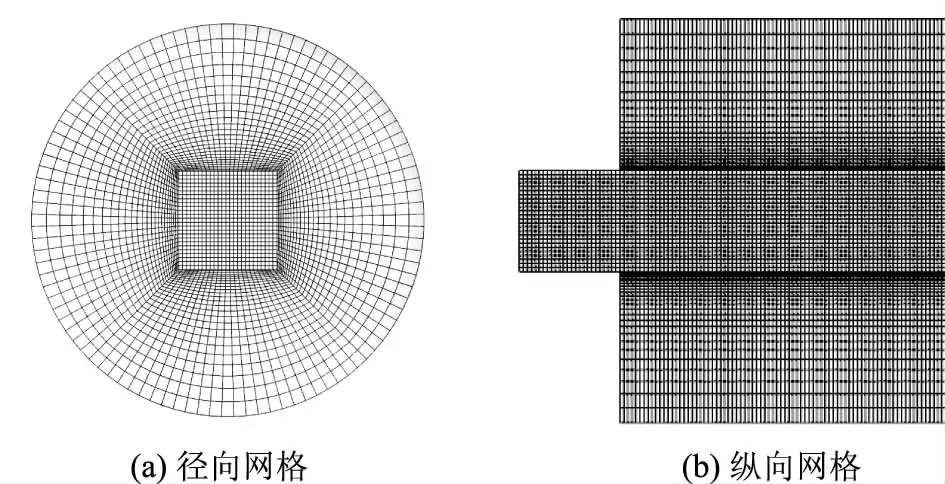
图2 计算域网格

现设计5种入口平均速度不同的计算方案，其分别为20、35、50、65、80m/s，速度变化在1.0～0.8u，为凸显涡结构的作用，取I=10%[20]。它们液体参数与计算工况如表1与表2所示。

2.2 模型验证

为便于对比，采用圆射流的数值计算结果来验证本文的数值模型。应用本文的数值模型对小尺度圆射流进行模拟，入口直径为2mm，平均速度为120m/s，湍流强度为5%，表面的液相体积分数为0.2，时间为0.0003s，如图3(a)所示。

表1 液体参数

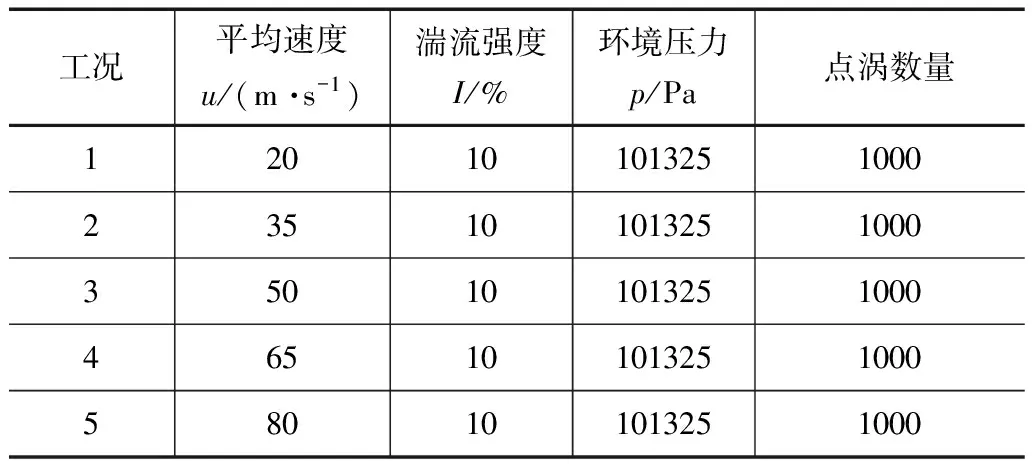
表2 计算工况

而文献21中，通过实验拍摄得到的圆形射流如图3(b)所示，其入口直径为2mm，时均速度约为98m/s[21]。

通过计算结果和实验结果的对比，在喷口附近，现有一段表面相对光滑的阶段，沿流向的后一段表面出现鳞状突起。两者射流表面的斑图基本一致，中心速度相差不大，说明本文的数值模型正确。

3 各工况计算结果与分析

使用本数值模型对上述计算工况1～5进行数值模拟，并对各工况结果中的水舌形变、掺气、涡结构、液滴分布进行分析。

3.1 水舌形变

观察计算工况1的液相体积分数为0.2的水舌，其整体形态如图4(a)所示，根据形变可以将水舌分为如下三个阶段。

初始阶段：入口附近的水舌呈现光滑表面，随后四条直角边开始出现起伏的“波浪”形状，并且形变逐渐加剧，成为“锯齿”形状，如图4(b)所示。

过渡阶段：表面的“锯齿”加深，逐渐形变成“丝状”形状，存在少量的液滴脱落，如图4(c)所示。

破碎阶段：直角边的“丝状”从中间断裂，破碎分离出大量的小液滴，如图4(d)所示。

高速矩形水舌的径向截面形状会沿流向距离发生变化。以计算工况1为例，在水舌的初始阶段，如图5(a)和图5(b)所示，其整体还能够保持着接近矩形的形状。在过渡阶段，即图5(c)和图5(d)，原来的矩形边界由直线逐渐形变成为波浪状，波峰波谷分布逐渐不规则，波峰越来与凸出，波谷也越来越凹陷，其四个顶角的形变较大。进入破碎阶段，即图5(e)和图5(f)，液滴大量脱落后，水舌截面边界线条逐渐圆润。由于重力的影响，截面整体形状接近水滴形状，上窄下宽，掺气程度也是上小下大。在整个水舌表面破碎的过程中，纵向的水舌截面未产生长轴与短轴的变换，即轴变换现象[22]，说明表面张力产生的毛细管效应不明显。

为了描述这种矩形水舌截面边界的形变，本文提出如下无量纲形变关系式：

图3 本文计算结果与文献21的对比图

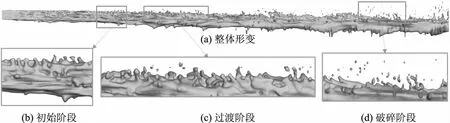
图4 t=0.03s，水舌的形变(水舌方向：自左向右)

(13)

式中,ζ为矩形“波浪”边界的形变参数；S—径向截面液相体积分数为0.98的等高线面积，m2；L—径向截面液相体积分数为0.98的等高线周长，m。

应用式(13)可以计算得出，圆，ζ=π/4；而正方形，ζ=1，可见形变参数ζ反映了正方形比圆的形变要大。当水舌截面产生“波浪”型边界时，其面积一定比相同周长下的正方形更小，ζ也随之变大，即“波浪”波高越大，“波浪”波长越小，ζ的值也越大。故无量纲形变参数ζ能够评价水舌截面的不规则形变。

5个计算工况下的形变参数ζ沿流向方向的变化如6所示。在计算工况1、2中，形变参数ζ都是先震荡增大后震荡减小，存在一个最大形变峰值，意味着水舌在运动过程中存在一个紊动到稳定的过程。而随着速度的增加，雷诺数也增大，最大形变发生的位置向后移动，从x/d=5后移到x/d=50，并且最大形变程度增大，从ζ=1.4346增大到ζ=2.9282，同时震荡强度也增强。

图5 t=0.03s，径向截面液相体积分数沿流向距离的变化

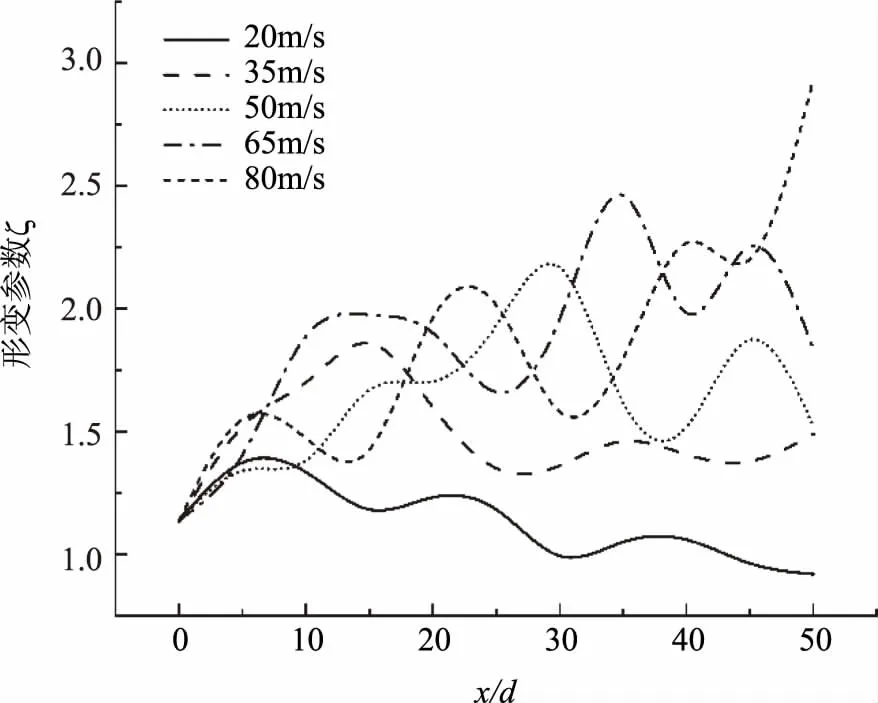
图6 形变参数沿流向的变化

3.2 水舌掺气

掺气程度也是水舌表面初次雾化过程中很重要的组成部分，本文提出无量纲的掺气面积比公式：

(15)

式中,C—掺气面积比；S0.20—径向截面中液相体积分数大于0.20的面积，m2；S0.98—径向截面中液相体积分数大于0.98的面积，m2。

各工况下，掺气面积比沿流向距离的变化如图7所示。由于液流速度与气相速度的差值大，两相交界面发生强烈摩擦，水舌掺气程度快速上升。其中，随着速度的增加，掺气程度的波动也越来越剧烈，峰值也随之增大。

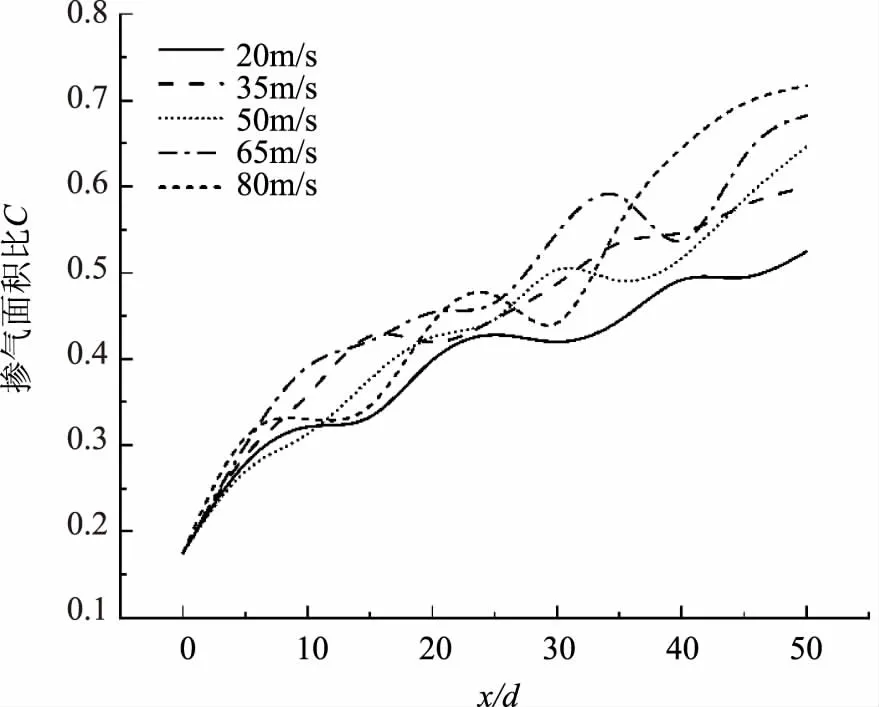
图7 掺气面积比沿流向的变化

3.3 涡结构与形变的关系

涡结构是影响水舌表面破碎的重要因素之一，可以通过涡量的大小来追踪涡结构，如图8所示。

在矩形水舌处于初始阶段时，即图8(a)至图8(c)，涡结构主要集中在入口内表面与水舌的表面附近，并且涡量极大，而水舌内部也存在部分离散的涡结构。

随着水舌流动，涡结构开始发展扩散，因为气相的密度比液相的密度小，更加容易受到涡结构的影响，所以涡结构主要是从液相向气相扩散，集中于水舌表面。从图8(c)和图8(d)可以明显发现，在水舌的过渡阶段中，形变部位附近涡结构集中，涡量较大，说明涡结构是导致水舌表面初次破碎的重要原因之一。

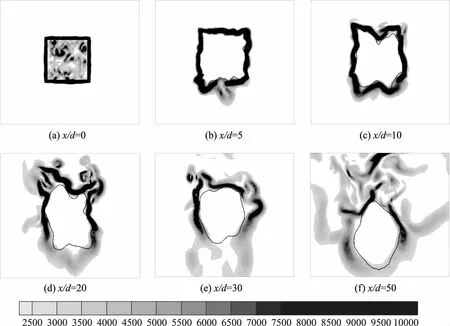
图8 t=0.03s时，涡量大小沿流向的变化

在矩形水舌的破碎阶段，即图8(e)至图8(f)，涡结构已经完全扩散至气相中，部分的涡结构开始脱落，并且在重力的影响下，主要集中于水舌的两侧与上侧。

3.4 液滴分布

使用液滴转换模型后，分离的液滴被转换为离散的粒子，图9与图10是其直径与空间的分布。

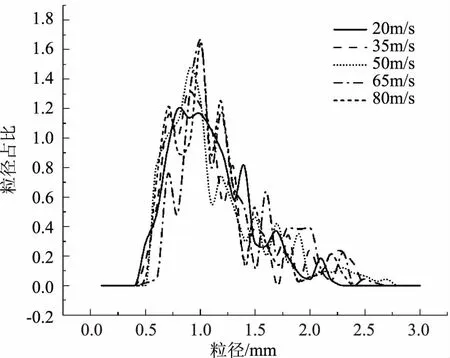
图9 液滴直径分布

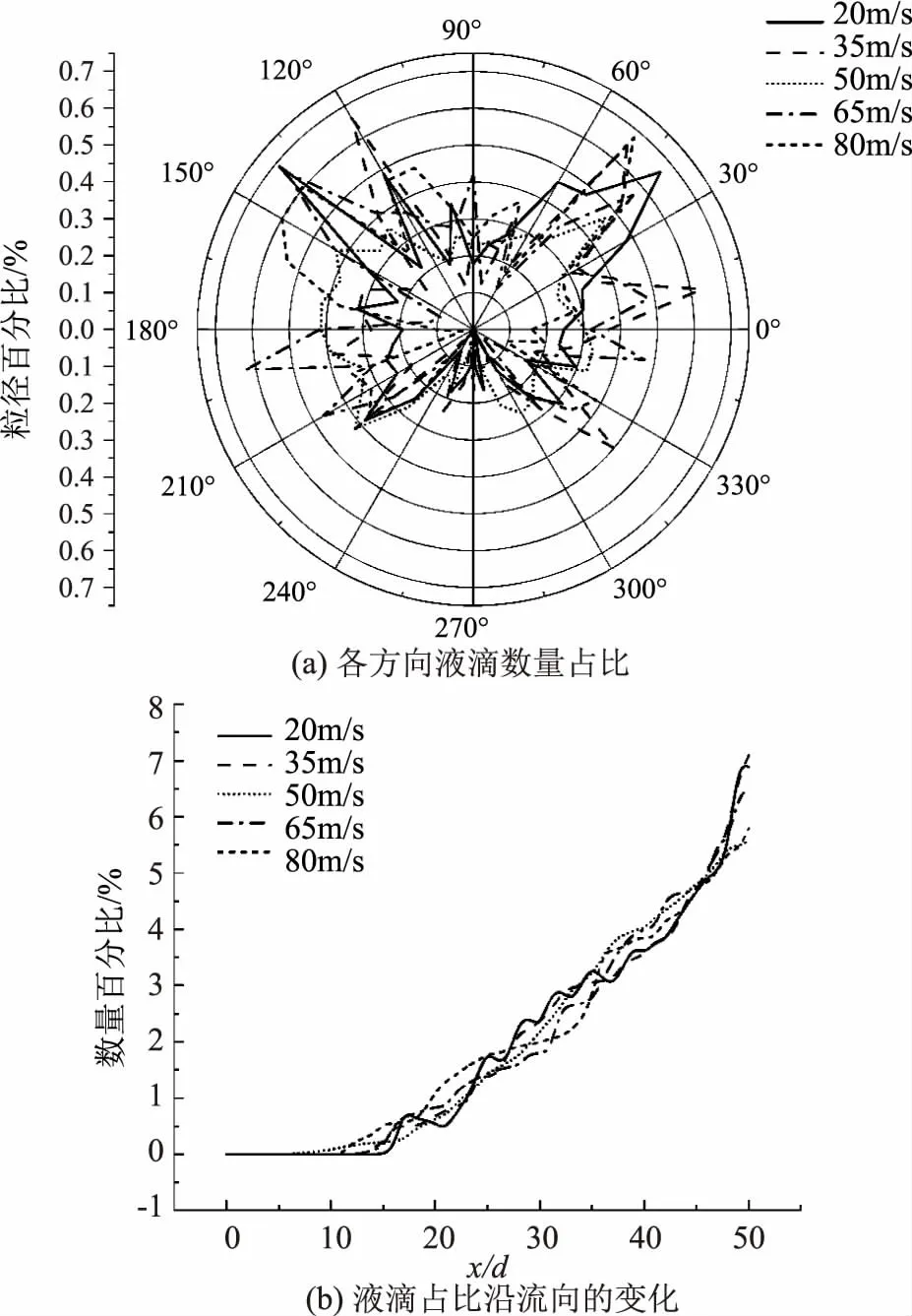
图10 液滴的空间分布

通过液滴的直径分布图，如图9所示，可以发现水舌表面在初次破碎后形成的小液滴的直径粒径范围在0.3～2.6mm，是一个“单峰”集中分布，其中主要集中在1.0mm左右。随着速度的增加，粒径分布更加集中，粒径占比的峰值也越大。

液滴在截面上的方向占比如图10(a)所示，破碎而出的液滴在水舌截面的上下部分的占比差异较大，在0°～180°内的液滴数量占比远远大于180°～360°的数量占比。说明在重力的影响下，水舌上表面比下表面更容易破碎，飞溅出更多的液滴。并且水舌截面的上部分中，45°与135°左右的液滴数量占比最高，而下部分的225°与315°左右的数量占比较大。主要原因在于顶点位置的液相与气相的接触面积更大，所受扰动更大，再加上涡结构的发展，导致顶点更容易形变凸出后分离液滴。说明矩形水舌在破碎过程中，最主要的喷溅点位于上表面的两个顶点附近的区域。

而图10(b)是液滴在流向方向上的数量分布。流向距离越远，分离出的液滴越多；速度越快，破碎距离越小，液滴也越早分离。

4 结论

本文针对高速矩形水舌的表面破碎过程做了数值模拟，得出以下结论：

(1)建立了高速矩形水舌运动的数学模型。在水舌入口处设置随机点涡阵来体现水舌入口处的随机扰动，模型能够刻画矩形水舌表面形变、表面破碎、液滴形成等过程。

(2)矩形水舌表面的初次破碎分为三个主要过程：初始阶段、过渡阶段、破碎阶段。涡结构最开始主要集中于水舌的内外表面附近，从水舌表面向气相发展、扩散、脱落，并在重力的影响下，集中于水舌的左右两侧以及上侧。速度越大，越早破碎。

(3)在重力与扰动的作用下，矩形水舌的初次破碎位置主要位于上表面的两条指直角边附近，液滴粒径为0.3～2.6mm，集中于1.0mm。入口平均速度越大，粒径分布越集中。