苏州河河口水闸闸门底轴转动变形测量方法研究
王 江
(上海勘测设计研究院有限公司,上海 200434)
苏州河也称吴淞江源于太湖,在苏州河河口汇入上海黄浦江,苏州河河口水闸是苏州河河口防潮、排涝等功能的重要控制建筑物[1]。水闸底轴直径2m,全长111.21m,为国内外规模最大的底轴驱动式翻版闸门。工程建设期间国内著名的院校及科研机构进行了多项试验及创新,比如同济大学、河海大学进行了水工建筑物有限元模拟及水闸整体分析;南京水利科学研究院、浙江大学进行了金属结构有限元模型分析及翻板门模型实验等[2]。鉴于底轴结构的重要性,闸门底轴采用了激光准直系统及静力水准进行自动化监测[3],但水闸自建成至今运行已达14年之久,闸门进行安全检测后发现底轴激光准直系统数据失真,底轴运行时存在径向位移,底轴中间波纹管密封系统局部失效,漏水量大,出现险情,对底轴进行径向位移测量及波纹管同步测量并制定修复方案迫在眉睫。针对闸门底轴圆心等结构部位转动过程中的实时高精度测量,国内、外学者研究相对较少,在空间精密测量领域国内外学者展开了丰富的研究,范春燕[4]采用高精度全站仪测量系统模拟全局测量空间构件实验,分析了不同平差方法的优劣;何应鹏[5]采用近景摄影测量与传统全站仪测量进行有机的结合,实现了无控制点的摄影测量方案;李洋、瞿剑苏等[6]采用激光跟踪仪与全站仪联合测试,实现了超长距离位置信息的标定。基于底轴运动特性,采用静态人工测量无法满足测试需要,采用全站仪自动跟踪测量技术对底轴进行动态测试能够满足精度及效率要求[7- 8]。
根据上述背景,本文通过简化底轴圆心变化及波纹管同步性测量模型,采用三维网严密平差方法建立了全局测量坐标体系,运用后方交会方法将3台全站仪测量坐标系联系到同一坐标系中进行底轴圆心变化跟踪测量。建立圆柱坐标系,通过全站仪跟踪测量,比较2个棱镜圆柱极坐标的轴向、径向、切向3个分量之差,计算中间波纹管南北转动同步偏差。
1 工程概况
苏州河河口水闸采用100.0m×7.76m翻板钢闸门,闸门底轴直接驱动旋转,转角范围0°~90°,全关时门叶呈竖直状,全开时门叶向外江侧卧倒呈水平状。闸门底轴分南、北两段,每段长度约55m,支承在10个支铰座上。底轴两端穿过启闭机房闸墙后与启闭机拐臂相连,拐臂后另设有1个固定支铰。南北轴中间断开,采用波纹管柔性连接,波纹管外设有橡胶密封套结构,穿墙止水采用盘根止水型式。水闸结构纵剖面图、横剖面如图1—2所示。
2 底轴圆心变化及波纹管同步性测量模型及测量方法
2.1 测量模型
苏州河河口水闸闸门底轴运行过程中存在轴向、
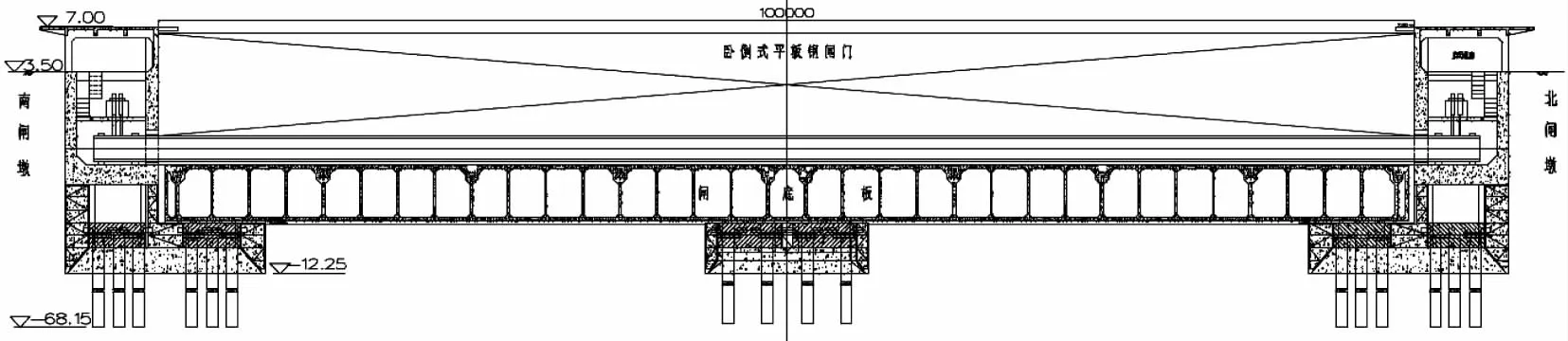
图1 水闸结构纵剖面图

图2 水闸结构横剖面图
径向等变形,需测量底轴转动过程中的圆心运动趋势、中间波纹管的同步性。经结构分析及模型简化,圆心变化测量测点分布于南北两端穿墙止水及中间波纹管处,如图3所示,中间波纹管转动同步性测点分布于中间波纹管南北两端,如图4所示。
2.2 测量技术方法
2.2.1全局测量坐标体系建立
为将底轴南、北两端的测量工作纳入一个全局统一坐标系,在底轴内建立测量控制网[9],如图5—6所示。底轴轴口两端布设不锈钢观测架A、B,用于安置全站仪或棱镜,同时在A、B处墙上布设8个棱镜(A1~A4、B1~B4)。考虑到观测场地狭窄,应拉大棱镜与全站仪的距离,高度角适中,棱镜张角尽量大。在底轴南岸A点安置全站仪,北端B点安置棱镜,采用全站仪多测回观测软件,自动观测5个棱镜(A1~A4、B)。同理在北端B点进行观测。
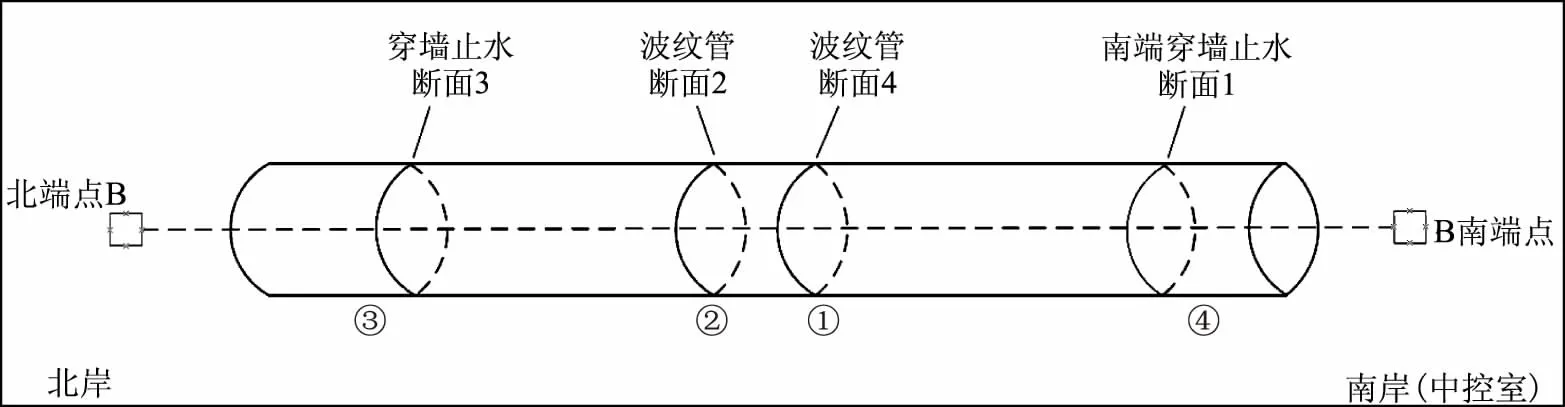
图3 底轴圆心变化测量断面模型

图4 中间波纹管南北两端同步性测量模型

图5 底轴坐标系统示意图
采用三维网严密平差方法[10],对多测回观测数据进行处理。定义A点的平面坐标为(0,0),以AB为x轴方向,y轴指向黄浦江侧。平差得到各点三维坐标见表1,平面坐标和高程中误差的均值为(0.40、1.50、0.79mm)。

图6 测量控制网示意图
2.2.2圆心变化测量方法
每个测试断面布设3个棱镜,在底轴轴口架设3台徕卡TS60全站仪[11],分别跟踪一个棱镜,如图7—8所示。3台全站仪测量坐标系由固定在墙上的4个棱镜和对岸棱镜通过后方交会方法确定,保证3台仪器测量坐标处于同一坐标系中。将坐标投影至o-yh断面,断面坐标系向东为y轴,向上为h轴,在断面内计算底轴圆心坐标。比较闸门处于各个开度时底轴圆心坐标,绘制底轴转动过程中圆心变化趋势曲线。底轴转动过程中,若未产生变形,则闸门处于各个开度时,底轴圆心坐标应一致。
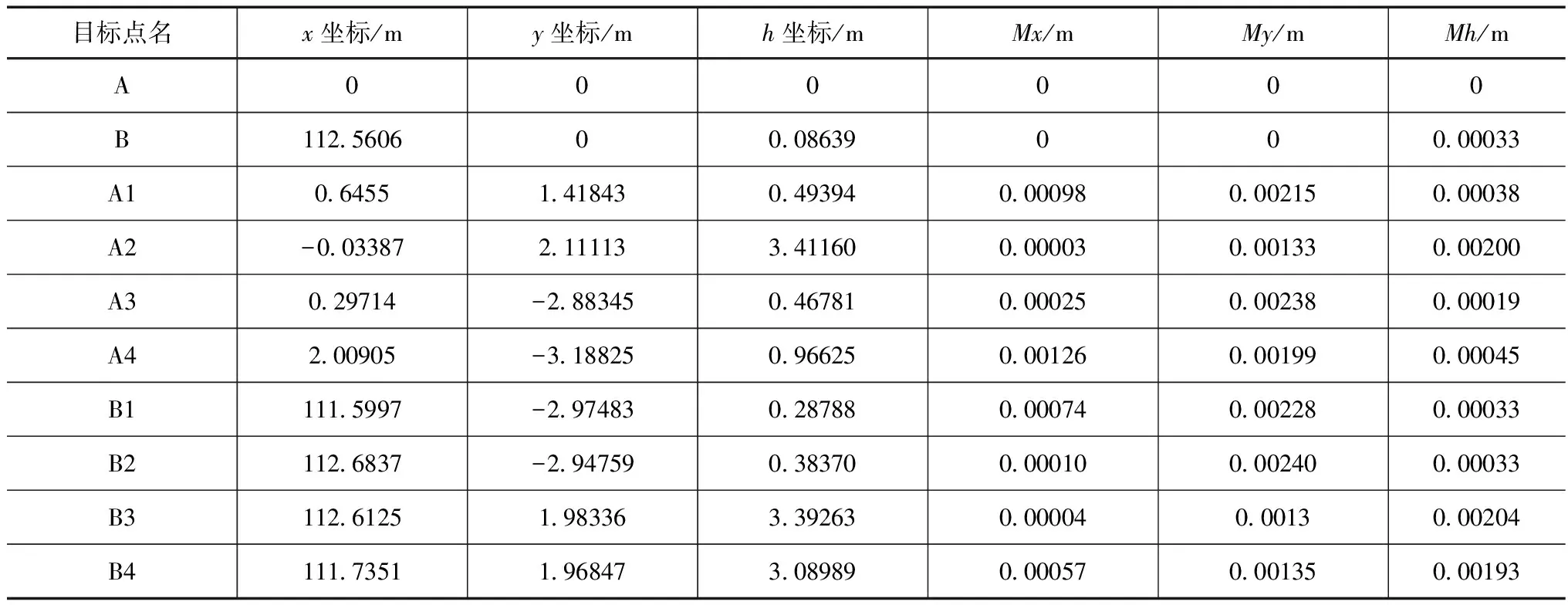
表1 控制点三维坐标
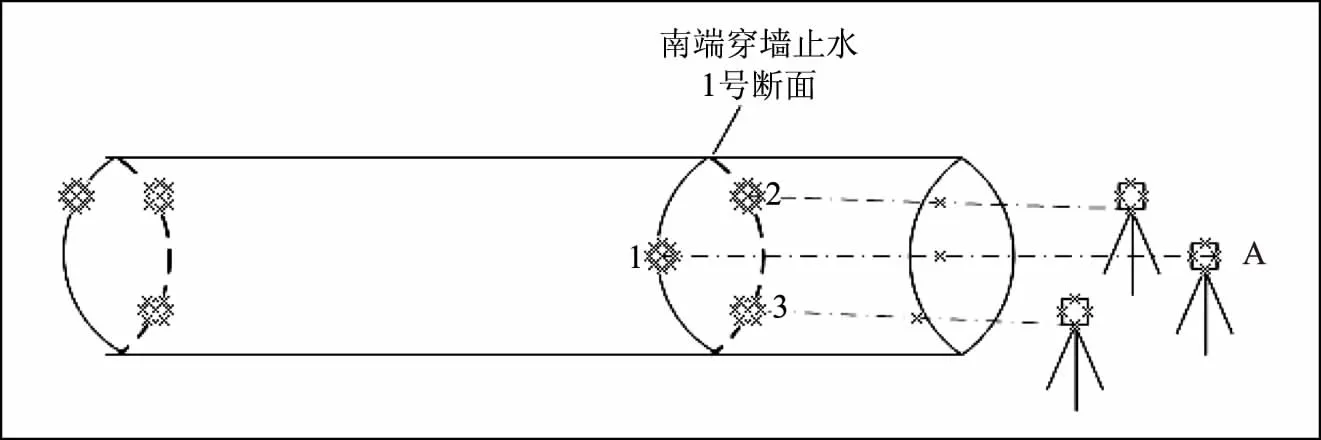
图7 圆心变化测量布置图

图8 圆心变化测量仪器安装实物图
2.2.3底轴中间波纹管同步性测量方法
(1)确定旋转轴,建立圆柱坐标系
在底轴南端分段布设4个棱镜,闸门处于挡水和卧底状态,分别观测其坐标,结果见表2。计算旋转轴在测量坐标系内的直线参数见表3。

表2 底轴南段的4个棱镜在闸门挡水和卧底状态的坐标 单位:m

表3 旋转轴的直线参数 单位:m
以x0、y0、h0为原点,建立圆柱坐标系,如图9所示,hh轴为旋转轴方向,xx轴垂直于旋转轴且在测量坐标系内向上,xx轴与h轴接近,yy轴在测量坐标系内向东且与xx轴正交,A-xyh为测量坐标系,同图5建立测量坐标系。
(2)测点布置及测量
南北底轴轴口A、B点各布置1台全站仪,中间波纹管南北两端各安装一个棱镜,底轴转动过程中每台全站仪跟踪一个棱镜,同步测量棱镜空间三维坐标(xyh)。
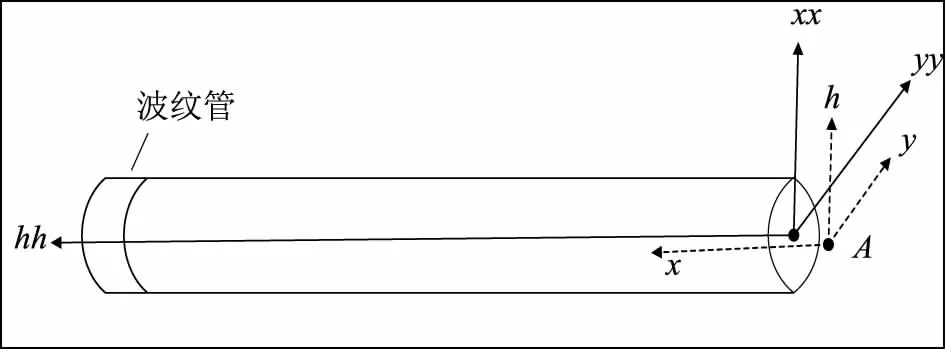
图9 圆柱坐标系示意图
(3)同步性计算
将2个棱镜的同步测量坐标(xyh)转换为圆柱坐标(xx、yy、hh),再换算成极坐标(p、sita、r),极坐标如图10所示,统计数据见表4。

图10 圆柱坐标系极坐标示意图

表4 棱镜空间三维坐标
两个测点圆柱极坐标的轴向、径向、切向3个分量之差如图11所示,即代表中间波纹管南北转动同步性,切向角度差乘以轴半径0.85m换算为切

图11 中间波纹管南北同步性分析图
向差。若底轴转动过程中,中间波纹管南北转动同步,则两个棱镜圆柱极坐标的3个分量之差(Δr、Δp、Δθ)应各为同一常数。
3 测量成果
3.1 测量水位信息
测量期间,内外河水位见表5。
3.2 底轴圆心变化测量结果
将底轴断面圆心坐标(y,h)作图,绘制圆心坐标的变化曲线,受文章篇幅限制,第一测回部分圆心位置变化如图12—15所示,☆为初始位置,Δ为最终位置,统计结果见表6。底轴转动过程中,南北两端穿墙止水处圆心较稳定,移动范围在mm级,数值在1.4~8.8mm之间,中间波纹管两侧处的圆心移动范围较大,达到cm级,数值在6.7~33.0mm之间。根据测试结果可知底轴旋转轴心不稳定,如图16所示,实际旋转轴并非为一固定轴线。

图12 断面1关闸底轴圆心位置分布变化(躺-立)

图13 断面2开闸底轴圆心位置分布变化(立-趟)

图14 断面3开闸底轴圆心位置分布变化(立-趟)
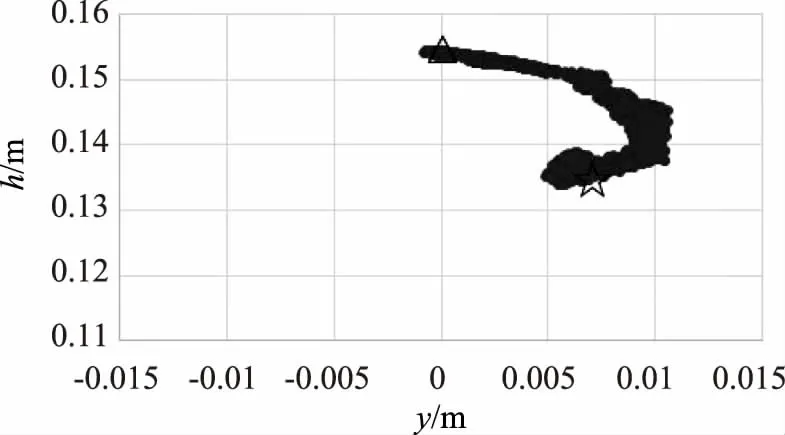
图15 断面4关闸底轴圆心位置分布变化(躺-立)

表5 观测期间内外河水位情况
表6 底轴圆心坐标统计结果 单位:m

图16 底轴不稳定示意
3.3 中间波纹管同步性测量结果
底轴中间波纹管南北同步性测量测试曲线如图17—18所示,同步性数据统计结果见表7。第一测回开闸初始径向距离差为-0.0423m,过程中最大变化幅度为4.7mm;初始切向距离差为0.0073m,过程中最大变化幅度为10.5mm;初始轴向距离差为0.5142m,过程中最大变化幅度为4.3mm;第二测回关闸初始径向距离差为-0.0414m,过程中最大变化幅度为4.4mm;初始切向距离差为0.0065m,过程中最大变化幅度为22.2mm;初始轴向距离差为0.5154m,过程中最大变化幅度为3.4mm。分析可知,底轴转动过程中,中间波纹管南北同步性,径、轴向同步性较好,变化幅度为mm级,数值在2.2~6.6mm之间;切向同步性较差,变化幅度为cm级,数值在10.5~22.2mm之间。
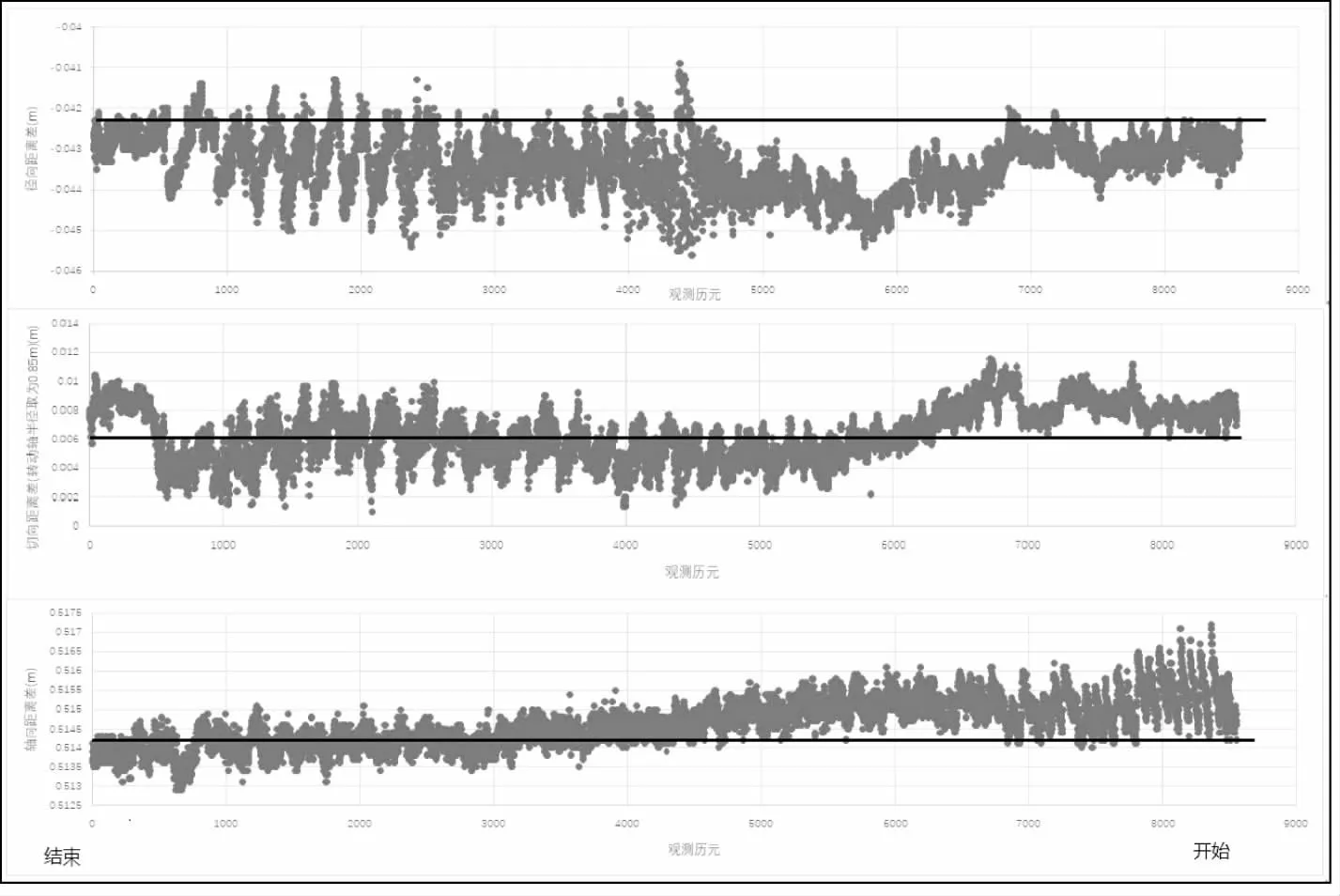
图17 开闸第一测回中间波纹管南北径向、轴向、切向同步性测试曲线

图18 关闸第二测回中间波纹管南北径向、轴向、切向同步性测试曲线

表7 同步性统计
4 验证性测量
由苏州河口闸整体三维有限元模型[12]及设计文件可知,整根底轴水平放在闸底板上,底轴每个断面的圆心高度一致。根据断面圆心测量统计结果可知两端圆心较中间圆心低,因此进行实测验证。选取底轴的两端和中部3个圆形断面,在底轴南侧A点架全站仪,调整全站仪的观测视线为水平状态。选取底轴南端的一个断面,钢尺倒挂紧贴底轴内侧量取断面的直径,全站仪打开激光器瞄准钢尺读取此时钢尺上激光点的值,盘左盘右测量取平均值;依次量取另外的两个断面,并记录读数。计算3处断面水平视线至圆心的距离,由表8及图19可知,底轴南侧穿墙止水处圆心较中间低4.71~5.45cm,底轴北侧穿墙止水处圆心较中间低3.31~4.05cm,即南北两侧的底轴中心轴线不平行且不重合。
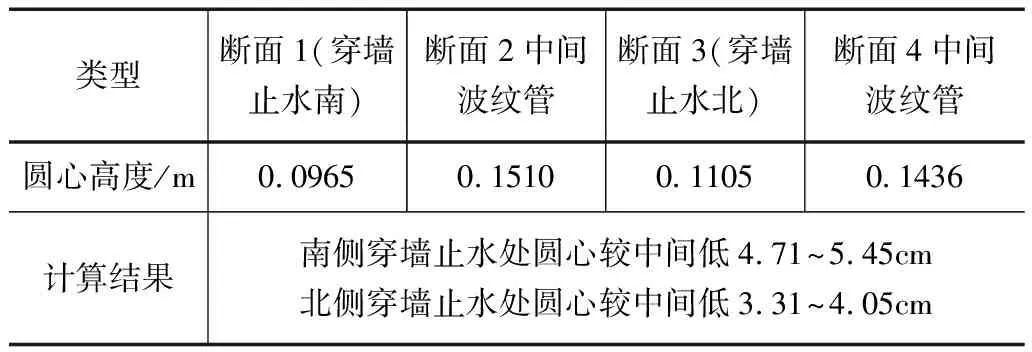
表8 断面圆心测量统计结果

图19 圆心位置关系实测结果
5 结语
(1)闸门底轴理论旋转轴是不存在的,受水位、启闭机工况等影响每次测量得到的是实际旋转轴,但底轴的实际旋转轴变动范围是有限的,采用全站仪进行底轴圆心变化跟踪测量及波纹管同步测量,分析底轴运行趋势是可靠且有必要的。
(2)底轴旋转轴不稳定对于底轴长期测量基准和分析基准的建立造成了一定的困难,可在长期测量基础上利用最小二乘圆柱拟合法建立底轴运动模型,得到底轴运动的最优轴线。该轴线可作为底轴监测数据分析的基准。
(3)闸门底轴位于苏州河河底,其环境比较潮湿,误差源主要为气象元素的测量误差,后期长期观测可通过小型百叶窗气象站完成气象数据修正。

