高阶常系数非齐次线性微分方程的新解法

丁小婷，姚晓闺，刘红琴

高阶常系数非齐次线性微分方程的新解法

丁小婷，姚晓闺，刘红琴

（陆军炮兵防空兵学院 基础部，安徽 合肥 230031）

通过引入常系数线性积分算子，得到了求解常系数非齐次线性微分方程的新方法，拓宽了教材中二阶常系数线性微分方程的求解范围，给出了更高阶的常系数线性微分方程的一般解法，将复杂问题简单化．通过例题验证了方法的可行性.

常系数；非齐次；线性微分方程；通解；积分算子

1 引言及预备知识

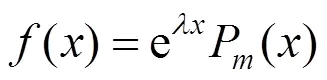
2 主要结果及证明

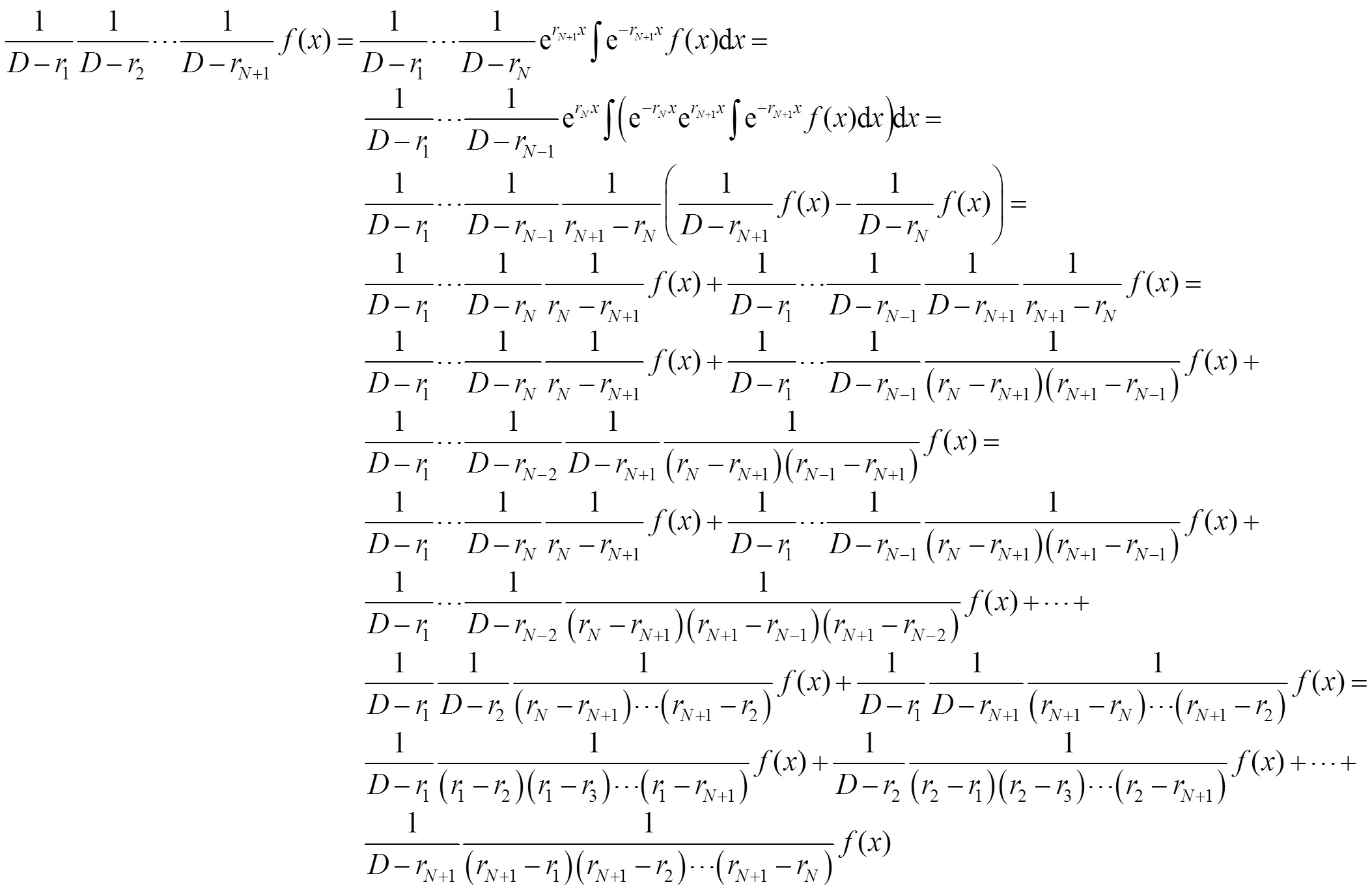
由数学归纳法可知，定理结论成立． 证毕．

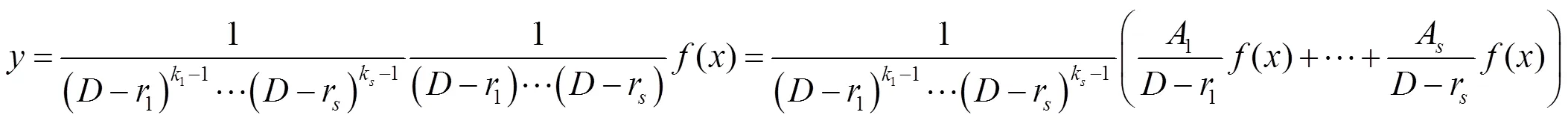
3　应用实例

[1] 同济大学数学系．高等数学：上[M]．7版．北京：高等教育出版社，2014．

[2] 丁同仁，李秉治．常微分教程[M]．北京：高等教育出版社，2000．

[3] 王高雄，周之铭，朱思铭，等．常微分教程[M]．北京：高等教育出版社，2012．

[4] 葛渭高，田玉，廉海荣，等．应用常微分教程[M]．北京：科学出版社，2004．

[5] 于亚峰．阶常系数线性微分方程的常数变异法[J]．贵州师范大学学报（自然科学版），2015，33（6）：83-86．

[6] 王钥．复高阶微分方程的解[J]．数学学报，2017，60（4）：651-660．

[7] 宋燕．高阶常系数非齐次线性微分方程的解法[J]．高等数学研究，2012，15（30）：22-23．

[8] 孙法国，任丽娜．四阶线性微分方程的算子解法[J]．西安工程大学学报，2009，23（6）：142-146．

[9] 郑华盛．高阶常系数非齐次线性微分方程的逆特征算子分解法[J]．大学数学，2014，30（4）：76-81．

[10] 宁荣建，时军．阶常系数线性微分方程和阶欧拉方程的积分因子解法[J]．大学数学，2017，33（5）：44-48．

A new method for solving high order non-homogeneous linear differential equation with constant coefficients

DING Xiaoting，YAO Xiaogui，LIU Hongqin

（Department of Basic Courses，Army Academy of Artillery and Air Defense，Hefei 230031，China）

By introducing constant coefficient linear integral operator，a new method for solving higher order non-homogeneous linear differential equation with constant coefficients was obtained．It widens the solution range of second-order linear differential equations with constant coefficients in the textbook，gives the general solution of higher order linear differential equations with constant coefficients and simplifies complex problems．Finally，the feasibility of the method is verified by an example．

constant coefficient；non-homogeneous；linear differential equation；general solution；integral operator

1007-9831（2022）03-0005-03

O175.1

A

10.3969/j.jssn.1007-9831.2022.03.002

2021-10-13

陆军炮兵防空兵学院2021年度教育教学研究项目（2021JGKT002）

丁小婷（1985-），女，安徽安庆人，讲师，硕士，从事微分方程研究．E-mail：540212180@qq.com