无网格动力分析的循环卷积神经网络代理模型1)

陈健 王东东 刘宇翔 陈 俊

(厦门大学土木工程系,福建厦门 361005)

(厦门市交通基础设施智能管养工程技术研究中心,福建厦门 361005)

引言

无网格法采用仅需位置信息的系列节点构造空间离散,具有离散形式灵活、形函数高阶光滑、计算精度高、后处理简洁等优点,因而在结构静动力分析方面得到了快速的发展和应用[1-9].但无网格形函数通常不是多项式、形式比较复杂,其影响域一般也大于传统有限元形函数,因而无网格法的计算效率相对较低[10-11].再者,无网格动力分析进一步将无网格空间离散和时间离散方法相结合,例如常用的Newmark 方法,需要逐步递推求解每个时间步的动力响应,更加剧降低了无网格法的计算效率[3,6].同时,每个无网格动力分析过程都是针对特定问题,给定条件的任何改变都需要对该问题重新进行递推动力计算,存在大量的冗余工作.因而提高无网格动力分析效率是无网格法研究领域的一个重要问题.

近年来,随着大数据与人工智能技术的迅速发展,数据驱动与人工智能计算力学的结合[12-13]逐渐兴起,有力促进了计算力学新方法的研究.例如,Oishi和Yagawa[14]利用机器学习模型处理复杂数据关系的强大能力,提出了一种基于人工神经网络的新型高效有限元刚度矩阵数值积分方法.李想等[15]探讨了机器学习与计算力学结合的不同形式.Tang 等[16]提出了一种基于数据驱动,能够将一维数据有效推广至三维情况的非线性弹性力学模型.Feng 等[17]将相场模拟与深度学习相结合,通过相场模拟准备结构裂纹扩展的图像数据,来训练卷积网络模型,从而判断出结构的剩余使用寿命.严子铭等[18]通过多种机器学习方法建立了页岩气采收率合理预测模型.阳杰等[19]应对数据驱动计算力学模型的训练阶段,提出了一种分层数据搜索方案,通过将训练集进行切割形成多层级子数据库,来降低模型训练过程中数据过滤的时间.黄钟民等[20]采用神经网络方法研究面内变刚度功能梯度薄板弯曲问题.

在提高无网格法的计算效率方面,除了发展高效无网格算法[6-10],机器学习领域的进展也为无网格法精度和效率的提升提供了新的途径.例如,Wang和Zhang[21]将机器学习中的全连接神经网络近似看作为形函数,提出了一种无网格形式的配点法.该方法无需事先假定形函数形式,其将网络损失函数采用变分形式构造,进而通过训练确定网络超参数最终获取数值解.Brink 等[22]将深度学习与配点法相结合,采用神经网络来确定基函数形式以及相关权重,在网络训练完毕后对非线性偏微分方程进行逼近求解.最近,刘宇翔等[23]基于卷积神经网络方法,提出了伽辽金无网格法形函数影响域的一种机器学习优化选择策略.在此基础上,本文通过研究无网格动力分析的机器学习代理模型,加速无网格动力分析的计算过程.

循环神经网络(recurrent neural network,RNN)是一类用于处理序列数据,具有记忆功能的递归神经网络,其内部信息通常按照数据序列顺序方向进行传递;由于其内置循环模块具有记忆性及参数共享等性质,因此在对序列信息的特征进行提取时具有良好的效果[24-25].该网络作为深度学习中的一类典型算法,被广泛应用于自然语言处理[26]、包含时间序列信息的数据特征提取[27]等.传统的循环神经网络在单个时间步上通常以一维向量的数据形式实现网络的训练和传递.然而,若将卷积神经网络(convolutional neural network,CNN) 引入循环神经网络,前者网络包含的卷积核具有权值共享特性,可以有效降低网络超参数训练量,防止过拟合情况发生,并且无需将多维数据信息展开为一维信息进行传递,充分保留了原始数据的空间信息.因此两种网络有机融合形成的循环卷积神经网络能够处理任意维度的数据形式[28],并充分提取数据在时间和空间上的双重特征,具有更广泛的适用性[29].

本文首先对比分析了无网格离散数据与深度学习训练样本、采用Newmark 方法的无网格动力分析流程与循环卷积神经网络序列信息传递模式之间的关系,揭示了无网格动力分析与循环卷积神经网络在计算流程与信息传递等方面具有输入和输出的内在一致性,建立了两者的本征联系.随后,基于该本征联系发展了与无网格法相匹配的循环卷积神经网络结构设计方法,进而提出了一种无网格动力分析的循环卷积神经网络代理模型.无网格动力分析的循环卷积神经网络代理模型充分吸收了无网格法节点模型离散灵活、数值样本精度高的优点,能够在保证精度的前提下显著提升无网格动力分析的计算效率.

1 无网格动力分析基本方程

1.1 无网格形函数

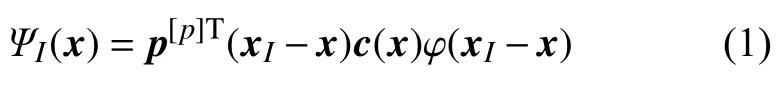
其中c(x) 为待定系数向量,φ(xI-x) 为核函数,本文中选为三次样条函数[1].p[p](x)为p阶基向量

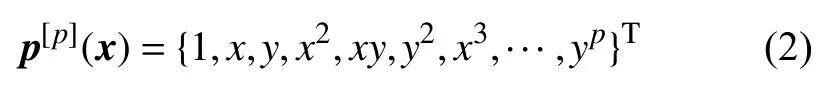
待定系数向量c(x)可通过施加下面的p阶一致性或完备性条件进行求解[2-3]

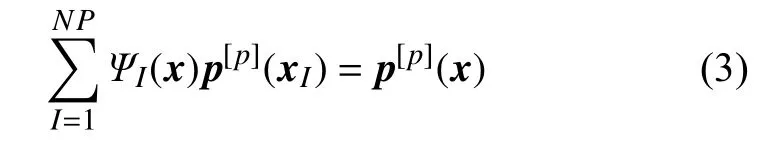
容易证明,式(3)等价于

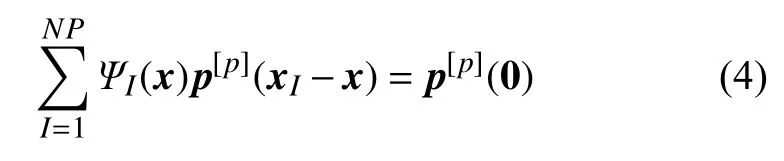
进一步将形函数表达式(1)代入式(4),有

式中A(x) 为矩量矩阵

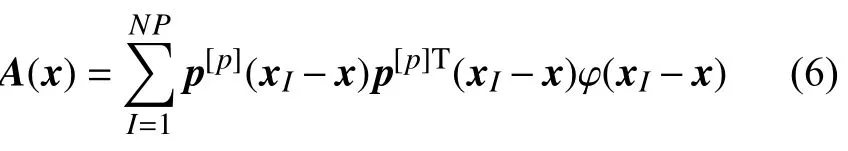
由式(5)可得c(x)=A-1(x)p(0),则式(4)定义的再生核无网格形函数变为

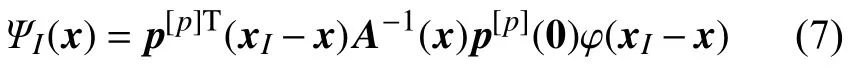
注意到无网格形函数 ΨI(x) 通常不具有插值特性,即 ΨI(xJ)≠δIJ,因而需要采用附加方式来施加位移边界条件[5].

1.2 弹性动力学控制方程及无网格离散

不失一般性,这里以弹性力学问题为例讨论无网格法动力分析的基本方程.对于空间区域 Ω 的弹性力学问题,其运动方程为

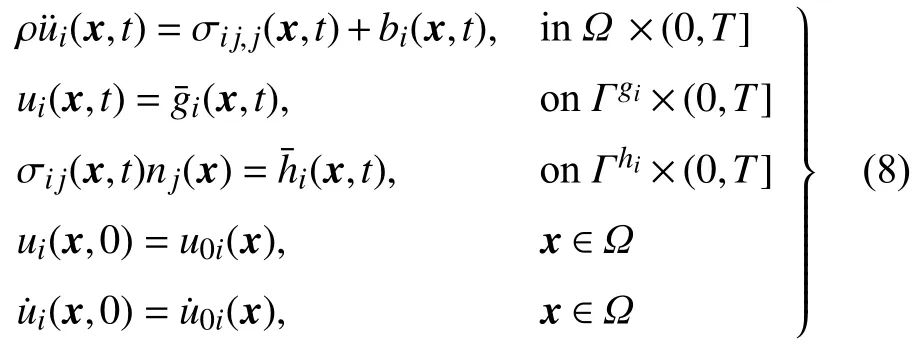
其中,i,j=1,2,···,nsd,nsd为空间维度,ρ为密度,ui为位移分量,σij为应力分量,bi为体力分量,u˙i和u¨i分别表示速度和加速度分量.T是动力分析总时长,和分别为强制边界和自然边界,nj为自然边界 Γhi的外法向量分量,和分别为强制和自然边界上给定的位移和面力分量,u0i和u˙0i为初始位移和速度分量.

如前所述,无网格形函数的非插值特性使得无网格法难以直接施位移制边界条件.针对该问题,本文采用Nitsche 变分方法引入位移边界条件,式(8)对应的等效积分弱形式为[30]

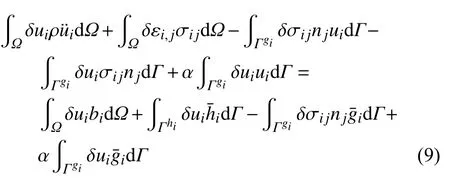
其中 α 为位移边界条件对应的罚因子.Nitsche 变分方法不仅保持了离散方程的对称性,同时降低了计算结果对罚因子的敏感性.

基于式(7)的无网格形函数,位移和加速度变量的离散形式为

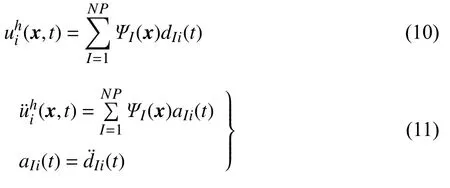
将式(10)和式(11)代入式(9),有

其中,a=为加速度系数向量,M和K为质量矩阵和刚度矩阵,f为力向量,它们分别对应的元素为

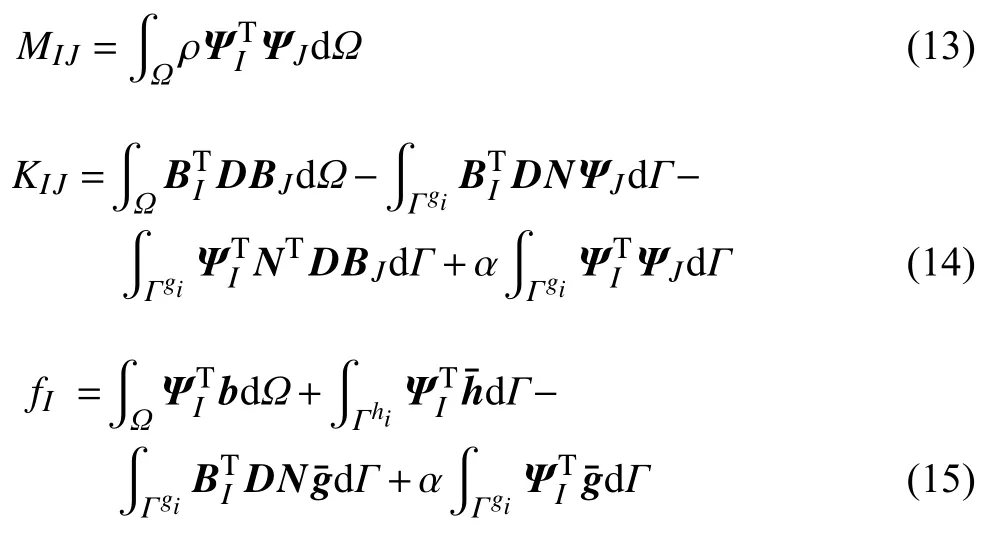
对于平面应力问题,式(13)～ 式(15)中的形函数矩阵 ΨI、位移梯度矩阵BI、方向矩阵N和弹性矩阵D分别为

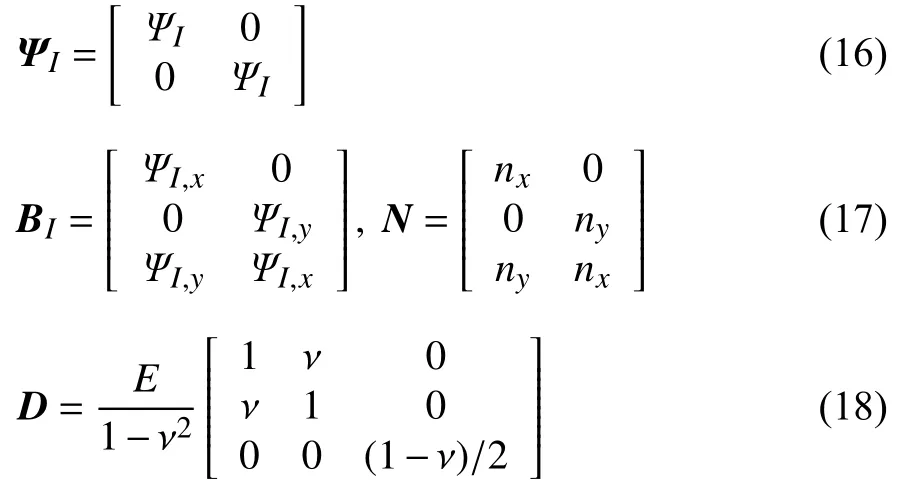
其中E和ν 表示弹性模量和泊松比.注意到式(13)中定义的质量和刚度矩阵都需要采用数值积分进行计算,但是由于无网格形函数不是多项式,因而传统高斯积分方法并不能保证无网格法数值积分的准确性.

为了提高计算效率,同时满足积分约束条件,即准确求解形式为p次多项式的解析解所需的积分条件,本文采用再生光滑梯度积分方法进行空间积分[10],将BI中的标准形函数梯度ΨI,x替换为再生光滑梯度[10].同时,为了保证数值实现的一致性,这里质量矩阵也采用再生光滑梯度积分方法进行数值积分.注意到再生光滑梯度积分方法的积分采样点具有全域等效积分点最少的特点,因此能够显著提高计算效率并保证最优收敛性[11].在再生光滑梯度理论框架下[10],无网格形函数的再生光滑梯度可以表示为

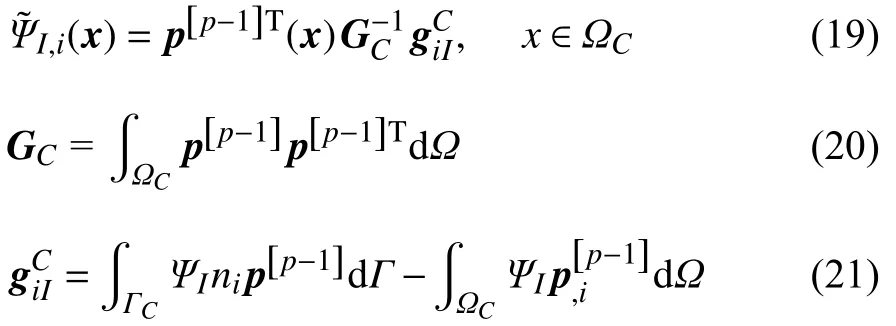
其中 ΩC为背景数值积分单元,ΓC为ΩC的边界,ni表示 ΓC的外法向量分量,p[p-1] 为(p-1) 阶基函数向量.方便起见,一般选三角形积分单元,此时GC可以解析计算.另一方面,对于向量,采用全域优化的内嵌一致的显式高效数值积分方法进行计算[10].

对于时间域,本文采用Newmark 法进行离散分析.便于时域积分起见,将时间域划分成一组等距的时间间隔,例如NT表示总的时间步数.Newmark 时间积分方法的预测-校正离散格式为[31]

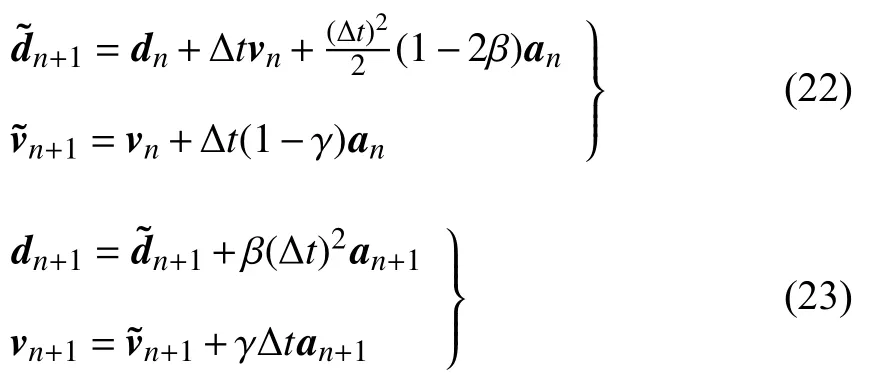
其中β和γ为积分参数,本文算例中取γ=1/2,β=1/4,此时Newmark 法即平均加速度法,具有二阶精度.将式(23)代入式(12)即可得到离散的无网格动力方程

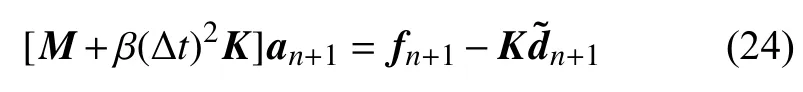
根据式(24)以及初始位移和速度条件,便可求出动力系统的整个时域响应.但是由于无网格法本身计算的复杂性,因此动力计算过程的效率较低,如何提升动力问题的计算效率是无网格法研究领域的一个重要问题.

2 全卷积与循环神经网络

2.1 全卷积神经网络

卷积层与转置卷积层是全卷积神经网络最具代表性的结构.与经典的卷积神经网络[17]相比,全卷积神经网络将前者网络结构中最后的全连接层部分替换为卷积层.如图1 所示,若卷积步长为1,其卷积层中的卷积运算过程为

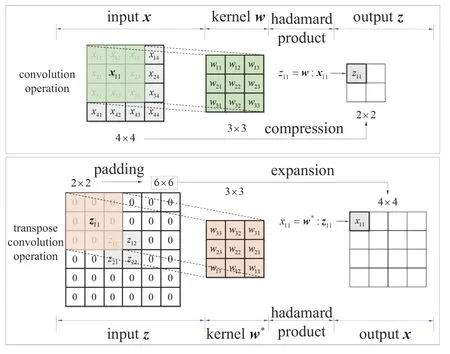
图1 全卷积神经网络中的卷积与转置卷积操作Fig.1 Convolution and transpose convolution operations in full convolution neural networks

其中xIJ表示矩阵x中位置为 (I,J) 的子矩阵,zIJ表示矩阵z中位置为 (I,J) 的元素;w为权重矩阵,又被称为卷积核,卷积核的尺寸与子矩阵xIJ的尺寸相同.式中“ :”表示双点积,即矩阵对应位置的元素相乘后再相加.

同时可见与卷积层相对应的转置卷积层中的运算过程,其计算方式是将输入样本尺寸通过填充0 元素进行放大后,再进行卷积操作.值得指出的是,转置卷积并不真正是卷积的逆运算,例如对于图中的输入样本x,经过转置卷积操作之后并不能恢复到原始的数值,只保留有原始的形状,即两种卷积过程只在形式上存在一定联系,而对应数值一般并不相同.

2.2 循环神经网络

循环神经网络(RNN)是一种应用于自然语言处理、语音识别等领域的特殊神经网络结构[25].与全连接神经网络和卷积神经网络相比,循环神经网络通过引入循环模块实现了一种“记忆”功能,即当前时间步的输出不仅与当前时间步的输入有关,还与之前所有历史时间步的输入-输出信息相关联.

同时,为了解决普通循环神经网络的长期依赖问题,在此引入长短期记忆神经网络(long short-term memory,LSTM)[24],以缓解随着循环次数增多而产生的梯度消失问题,进而更好地利用前面的历史信息来加强网络的学习.如图2 所示,LTSM 网络的特点在于通过其内部被称为“门”的结构,对信息进行选择性遗忘、增填及更新,其中包含“遗忘门(forget gate)”、“输入门(input gate)”和“输出门(output gate)”.循环模块中包含的 S和T 分别表示典型的S i g m o i d和T a n h 激活函数:S(x)=1/(1+e-x),T(x)=(ex-e-x)/(ex+e-x),网络中主要通过这两个激活函数对历史信息进行筛选控制.下面对各个“门”进行简要分析.

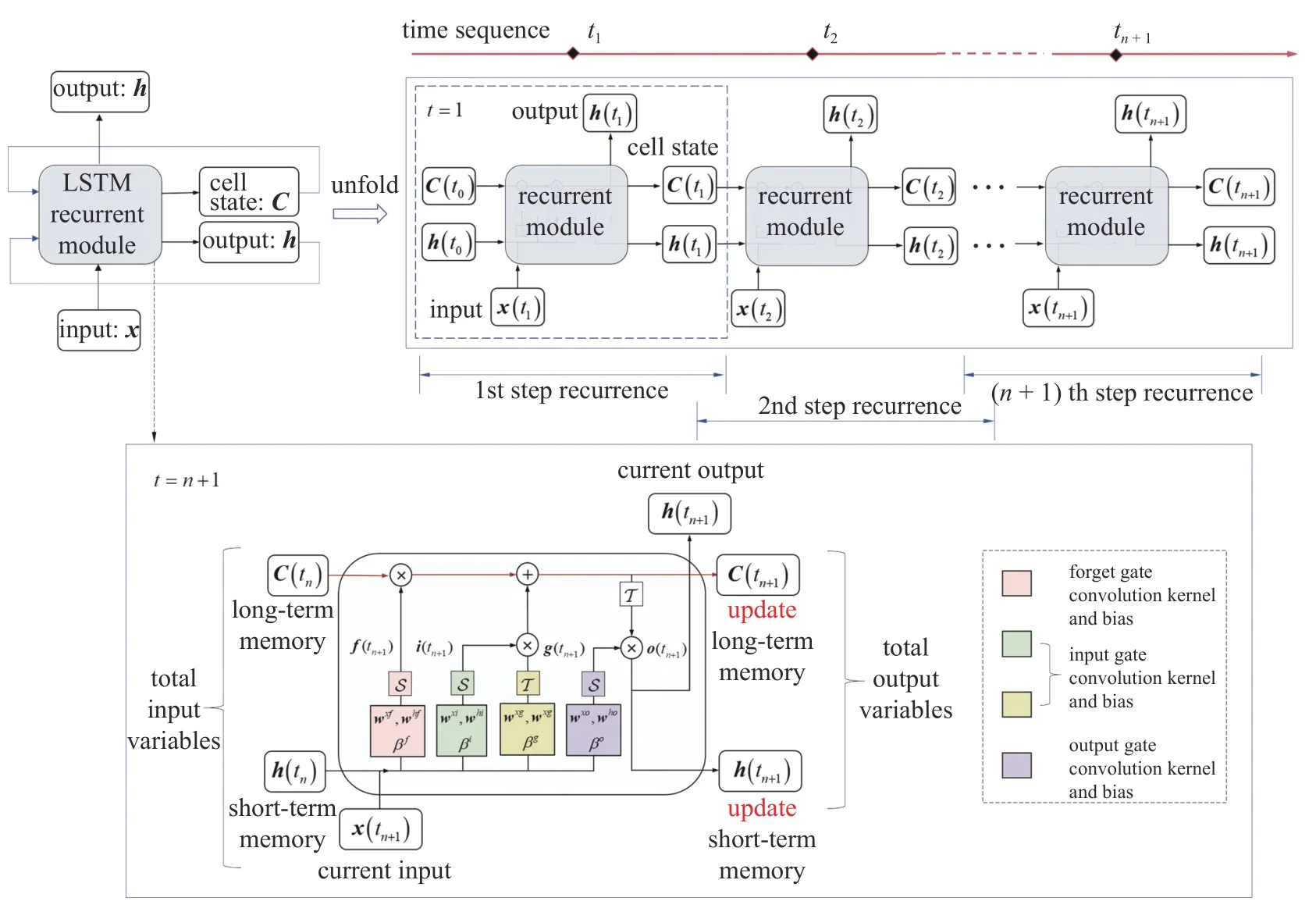
图2 LSTM 循环神经网络结构框架与循环模块Fig.2 Schematic illustartion of LSTM and recurrent module

首先,信息经过遗忘门的过程可描述为[25]

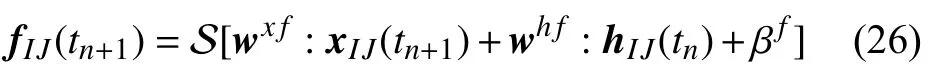
其中,xIJ(tn+1) 为时间步tn+1时刻输入变量x(tn+1) 的(I,J)子矩阵,hIJ(tn) 为上一时间步tn时刻输出变量h(tn)的 (I,J) 子矩阵.wx f和wh f为输入变量x和h对应的卷积核,βf为二者卷积核偏置之和.该过程读取上一时间步输出h(tn)和新时间步输入x(tn+1),通过学习训练输出数值为0～ 1 之间的遗忘因子f(tn+1),并与上一时间步的单元状态C(tn) 相乘实现选择性遗忘功能.

对于输入门,其功能是控制当前时间步单元状态C(tn+1) 的输入信息,在此过程中,输入变量x(tn+1),h(tn)通过卷积核及偏置wxi,whi,βi筛选,留下可进入的候补信息i(tn+1)

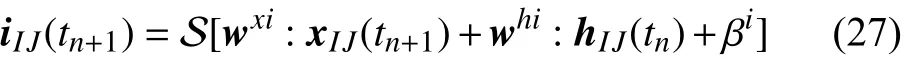
此外,通过卷积核wxg,whg及对应偏置量βg的筛选,留下可进入的候补信息g(tn+1) 为

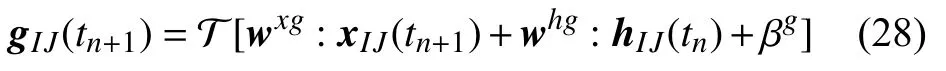
最后,输入变量x(tn+1)和h(tn) 经过“输出门”,通过卷积核wxo和who及偏置量βo来提取出直接组成最后输出h(tn+1) 的部分信息o(tn+1)

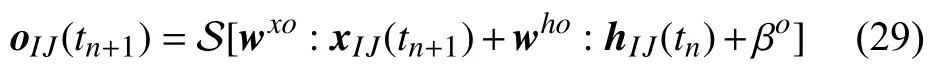
因此更新后的单元状态C(tn+1)和输出h(tn+1) 分别为

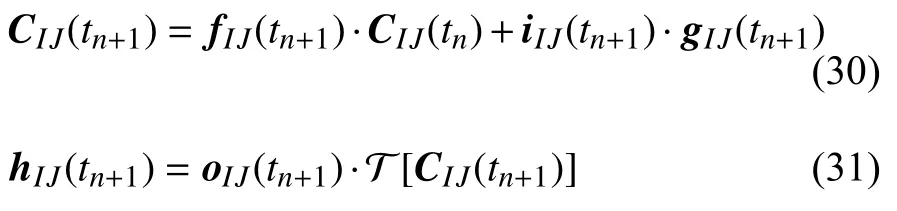
变量C(tn+1)和h(tn+1) 分别将作为长期记忆和短期记忆,进入到下一时间步的循环之中.

3 无网格动力分析的循环卷积神经网络代理模型

3.1 无网格数据与机器学习模型样本的匹配性

网络模型的预测能力依赖于训练数据集的质量.合适的数据集不仅需要数据内部存在本征联系,而且数据蕴含的多样性同样重要.在准备神经网络的训练数据集时,需预先确定训练样本的尺寸大小,与之对应的是相同尺寸大小的离散数据量和训练样本.同时,为了使得神经网络的预测能力具有高度泛化特性,需要在准备数据集时尽可能地考虑工况的多样性,例如边界条件施加方式、计算区域形状等,并通过不断模拟这些条件的变化来持续丰富数据集.

如图3 所示,无网格法仅通过节点离散进行计算分析,在空间离散形式上具有高度灵活性,能够确保节点数目与机器学习样本尺寸的匹配性,同时由于无网格形函数的高阶光滑特性,可获得高精度的数值结果样本.与之相对应,基于有序单元离散的有限元法,在节点数目确定后,对于不同计算模型,难以保证在离散分析过程中不出现为了匹配节点数目与机器学习样本尺寸而产生的单元畸变,从而导致结果样本精度的明显下降.

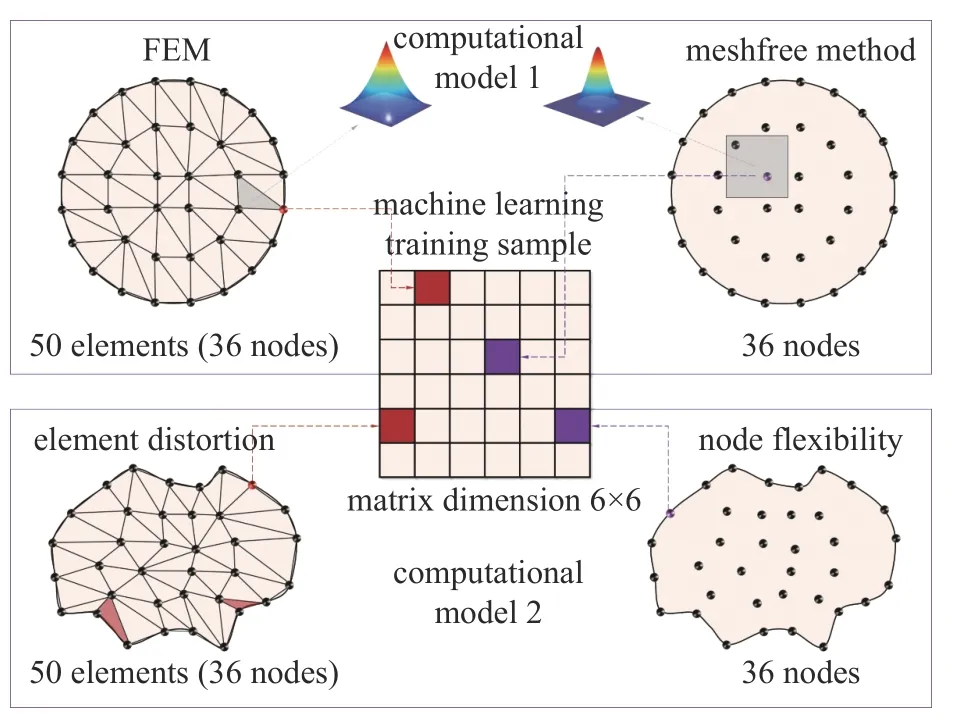
图3 数值计算产生数据与机器学习训练样本之间的对应关系Fig.3 Schemetic illustration of the corresponding relationship between the data generated by numerical simulations and the machine learning training samples

3.2 无网格动力分析与长短期记忆神经网络传递过程的本征联系

在采用Newmark 法的无网格动力分析中,可将整个流程分为计算阶段和传递阶段,两个阶段交替进行.

(1) Newmark 方法计算阶段

将每个新时间步的外荷载fn+1和上一时间步求得的位移、速度和加速度向量 (dn,vn,an) 作为输入,可以通过式(22)～ 式(24)得到该时间步的位移、速度和加速度 (dn+1,vn+1,an+1) .方便起见,将位移和速度更新过程表示为

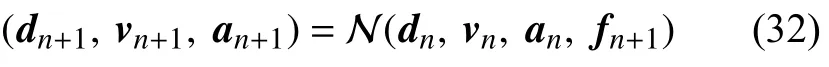
其中,N(·) 表示式(22)～ 式(24)的计算过程.

(2) Newmark 方法传递阶段

当从计算阶段求得第n+1 个时间步的位移、速度和加速度 (dn+1,vn+1,an+1),该信息将继续沿着时间坐标传递,参与到第n+2 个时间步的计算阶段,之后循环往复直至计算结束.

综合Newmark 法的计算阶段和传递阶段,可将采用Newmark 法的无网格动力分析作为一个在离散时间点上进行计算的序列问题,其中每一个时间步的计算都需要利用上一步计算得到的历史信息.

与采用Newmark 法的无网格动力分析相对应,长短期记忆神经网络同样可以分为计算阶段和传递阶段.

(1) LSTM 网络计算阶段

对于长短期记忆神经网络,在计算阶段中由上一步的输入变量Cn和hn,再结合新时间步的输入变量zn+1,给出该时间步的输出变量Cn+1和hn+1

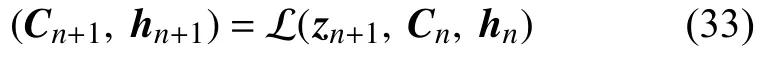
其中,其中 L(·) 表示式(26)～ 式(31)的计算过程.

(2) LSTM 网络传递阶段

在长短期记忆神经网络中,经过第n+1 次循环的计算阶段,可以得到单元状态Cn+1和输出变量hn+1,其中包含了经前若干模块逐个处理后的信息,然后继续将信息向第n+2 次循环传递长期和短期记忆.

图4 分别给出了采用Newmark 方法的无网格动力分析过程与长短期记忆神经网络传递过程.两者的对比分析表明,无网格动力分析与长短期记忆神经网络在计算流程与信息传递等方面具有内在一致性和本征联系,例如荷载与输入相对应,位移与输出相对应,加速度和速度与单元状态相对应,Newmark 时间积分与长短期记忆循环模块相对应等.此外,注意到无网格形函数的影响域和卷积神经网络核函数的感受野也存在相似关系[23].因此,可以利用该本征联系,发展无网格动力分析的循环卷积神经网络代理模型,从而提高无网格动力分析的计算效率.

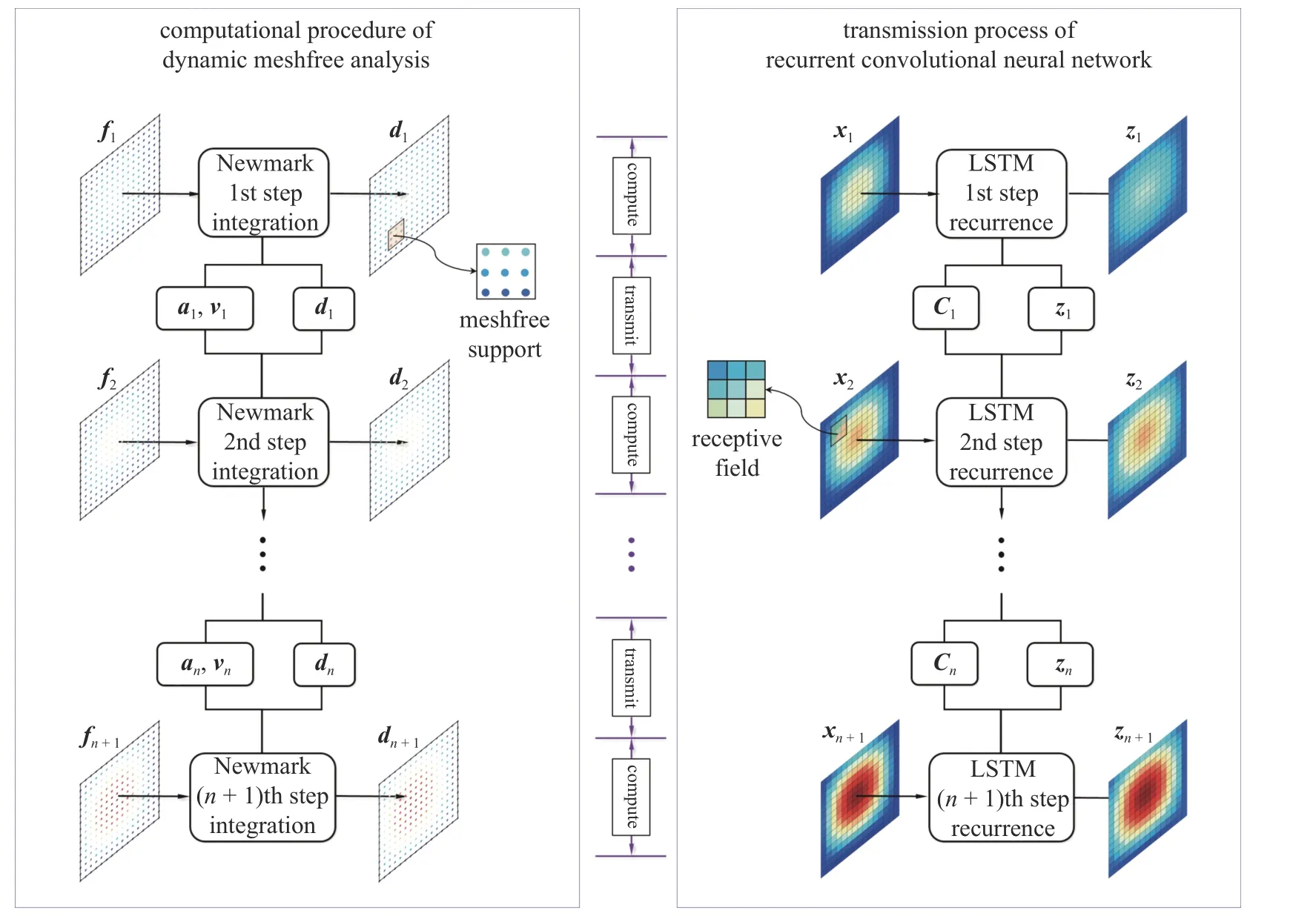
图4 无网格动力分析与长短期记忆神经网络之间的本征联系Fig.4 Intrinsic relationships between dynamic meshfree analysis and long short-term memory neural network

3.3 基于循环卷积神经网络的无网格法代理模型设计

将全卷积神经网络与循环神经网络进行结合,建立无网格动力分析代理模型,目的是分别提取数据的空间信息和时间信息,对无网格动力分析过程进行预测.针对代理模型构建,首先应匹配网络的输入输出样本尺寸和无网格离散形式.在网络训练过程中,将每个离散时间点上的力向量矩阵作为输入,以位移、速度、加速度等场变量的数值解矩阵作为输出进行学习.当所设计的神经网络训练完成之后,即可封装成为代理模型,然后向其输入任意离散时间步上的力向量矩阵,就可快速预测出当前时刻对应的无网格数值解.

图5 所示为无网格动力分析代理模型框架图,其中无网格动力分析的循环卷积神经网络设计借鉴了U-Net 网络结构中的卷积过程,同时引入长短期记忆循环模块.在该网络中,首先通过多个“卷积-激活函数-最大池化”模块,将输入信息进行压缩得到特征,然后将压缩后的特征输入至长短期记忆循环模块中提取时序信息,最后通过“逆卷积-激活函数-最大池化”模块过程将特征信息进行扩充得到输出,其中卷积与转置卷积模块使用的激活函数为Leaky ReLU 函数[32].采用MSE(mean squared error)误差来衡量迭代学习过程的收敛性,其定义为

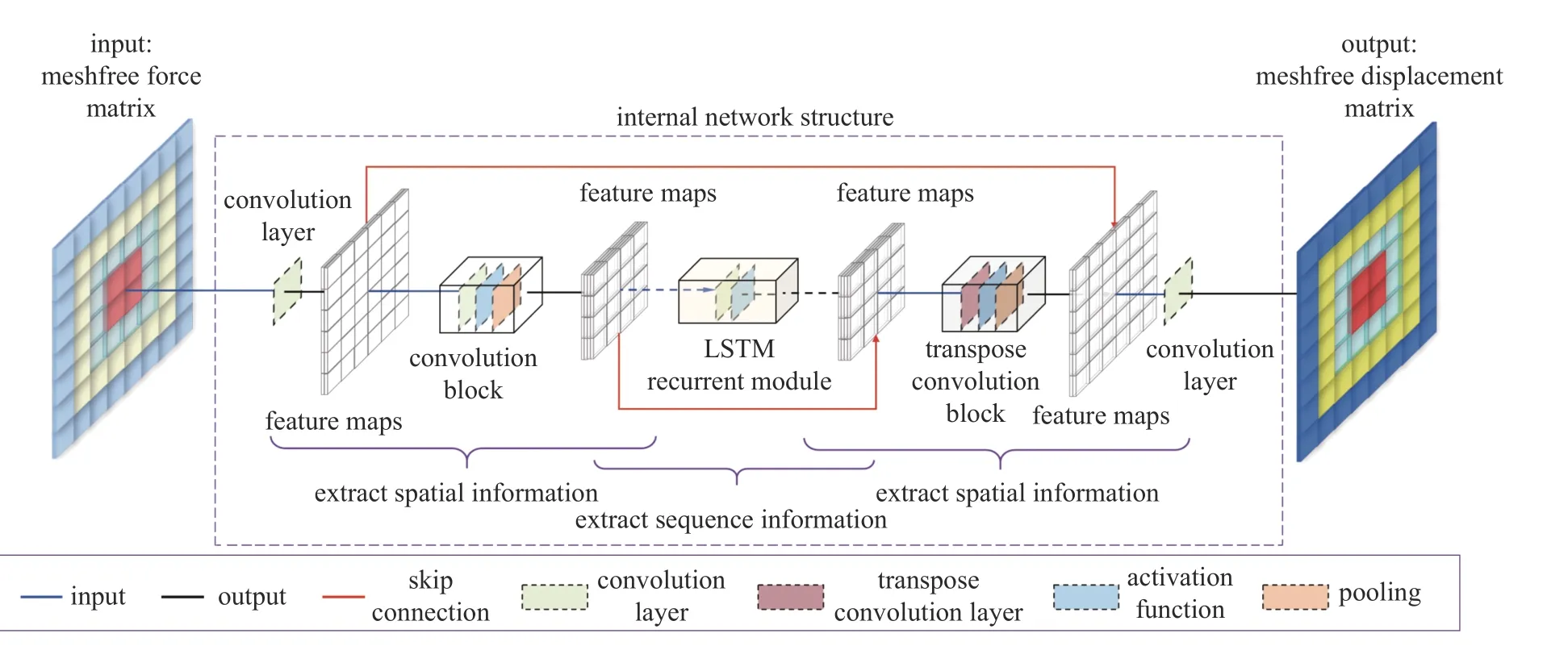
图5 无网格动力分析的循环卷积神经网络代理模型框架Fig.5 The structure of recurrent convolution neural network surrogate model for dynamic meshfree analysis

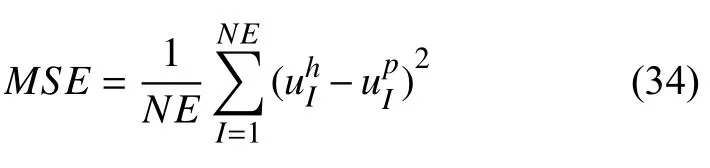
4 数值算例

4.1 数据集准备

为了说明无网格动力分析的循环卷积神经网络代理模型的构造过程和预测准确性,本文考虑图6所示的4 种不同区域的弹性力学问题作为训练目标,其中弹性模量和泊松比分别为E=2×107,ν=0.3 .算例均采用 32×32=1024 个节点的无网格离散,然后通过无网格计算准备训练数据,与神经网络的输入输出尺寸相匹配.这里考虑不同形状计算区域是为了增强网络的预测能力,提高代理模型的泛用性.本文代理模型的泛用性主要包含两方面,其一针对的是数据结构,即所提基于无网格法的代理模型可接受任意维度的数据.当求解区域的形状、边界条件等发生改变时,仅需重新准备相应数据集,无需改变网络结构便可进行训练,完成无网格动力分析数值解预测.其二针对的是求解问题类型,当数据集经过积累变得愈加丰富时,所能求解的问题类型也会随之增多.同时,本文考虑如下的多项式与三角函数两种不同形式的精确解

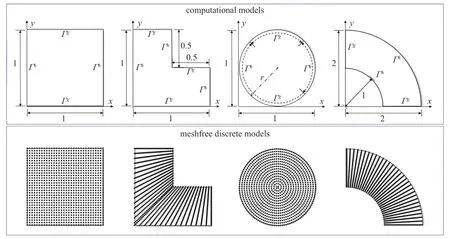
图6 无网格动力分析训练集包含的计算模型与离散模型Fig.6 Computational models and discretizations for the training set of dynamic meshfree analysis

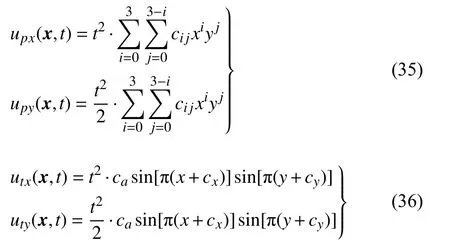
其中t∈[0,1].式(35) 中系数cij和式(36) 中系数{cx,cy,ca}均是定义在一定范围内的随机数,具体如下

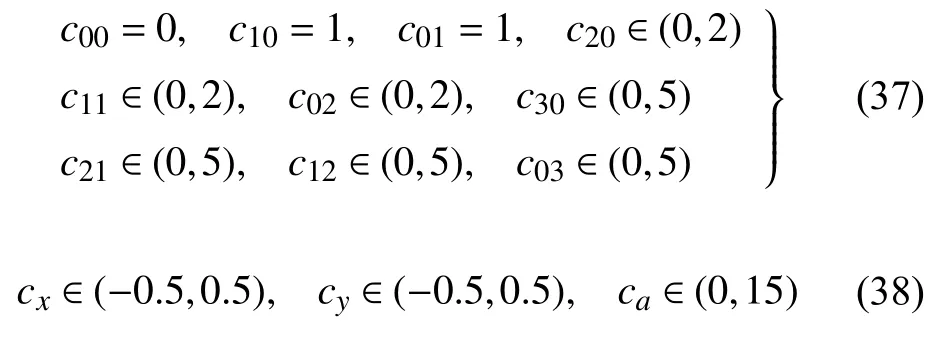
注意到这里给出精确解仅是为不同计算模型提供体力项和边界条件,而通过无网格计算生成的数值解,才是用于训练的数据集.

无网格计算中采用二次基函数,数值积分采用RKGSI 积分方法[10],时间积分步长为 Δt=0.002 s,总时间步数为500.为使网络模型更具有代表性,同时简化网络训练,每间隔50 个时间步提取一次信息,共计提取 11 个时间步的信息.此外,为统一输入输出矩阵尺寸,将尺寸为 2048×1 的每个时间步的力向量中每一个节点的值按节点位置排列成 2×32×32 的矩阵形式.由于共有11 个时间步信息,将这11 个时间步重新排列的力向量矩阵按时间顺序堆叠为11×2×32×32的矩阵.同样,无网格数值解也按时间顺序和节点位置排列成 11×2×32×32 的矩阵.至此,无网格动力分析的循环卷积神经网络训练方案中所有的输入输出信息,均已准备完毕.在本次训练中,对每一种不同的几何边界问题,多项式精确解与三角函数精确解均各计算1500 组样本,其中1200 组样本作为训练集,250 组样本作为验证集,50 组样本作为测试集,因此总训练集数目为4×1200×2=9600组,总验证集数目为 4×250×2=2000 组,总测试集数目为 4×50×2=400 组.

4.2 网络具体参数与训练情况

本文采用基于梯度下降算法的Adam 优化器进行网络参数训练.图7 给出了本文所提出的无网格动力分析网络代理模型的具体数据传递过程.同时,为保证参数训练效果,对网络参数采用Xavier 正态分布进行初始化处理,相应的网络代理模型参数收敛特性见图8.图8 结果表明,损失函数MSE的值随迭代次数的增加而逐渐减小,因此证明无网格动力分析网络代理模型的参数具有良好的收敛特性,其预测准确性随迭代过程不断提高.

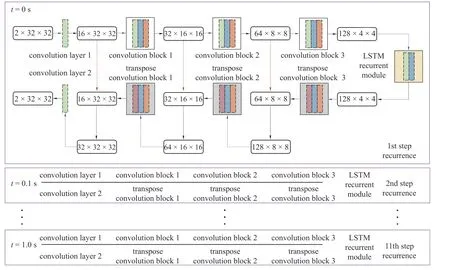
图7 无网格动力分析的循环卷积神经网络代理模型具体数据传递过程Fig.7 Detailed data transfer process of the recurrent convolution neural network surrogate model for dynamic meshfree analysis

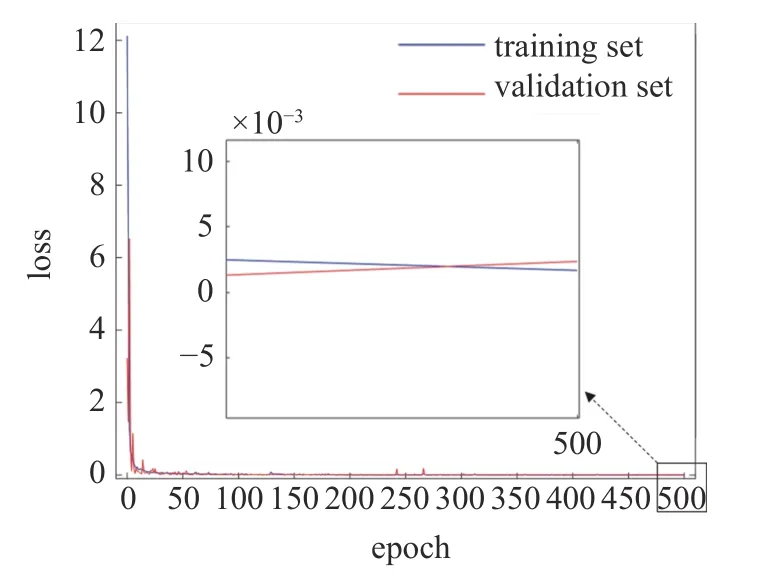
图8 无网格动力分析的循环卷积神经网络代理模型训练历史Fig.8 Training history of the recurrent convolution neural network surrogate model for dynamic meshfree analysis

4.3 预测结果

图9～ 图12 给出了基于无网格动力分析的循环卷积神经网络代理模型,对无网格动力分析数值解的预测结果.对于4 种不同形状区域的弹性力学问题,在t=0.6 s和t=1 s 两个时间节点分别列出了一组随机多项式测试样本的预测结果以及一组随机三角函数测试样本的预测结果.图中预测解和分别表示无网格动力分析的循环卷积神经网络代理模型预测所得到的x和y方向的位移结果,数值解和分别表示直接采用无网格动力分析方法得到的x和y方向的位移数值解,和表示代理模型预测结果与无网格法动力分析数值结果两者之间的差异.可以看出,对于解析解为多项式和三角函数的不同形状弹性力学问题,基于无网格动力分析的循环卷积神经网络代理模型得到的预测解和无网格动力分析数值解均吻合良好,表明本文所提的循环卷积神经网络代理模型能很好地预测弹性动力分析的无网格数值解.

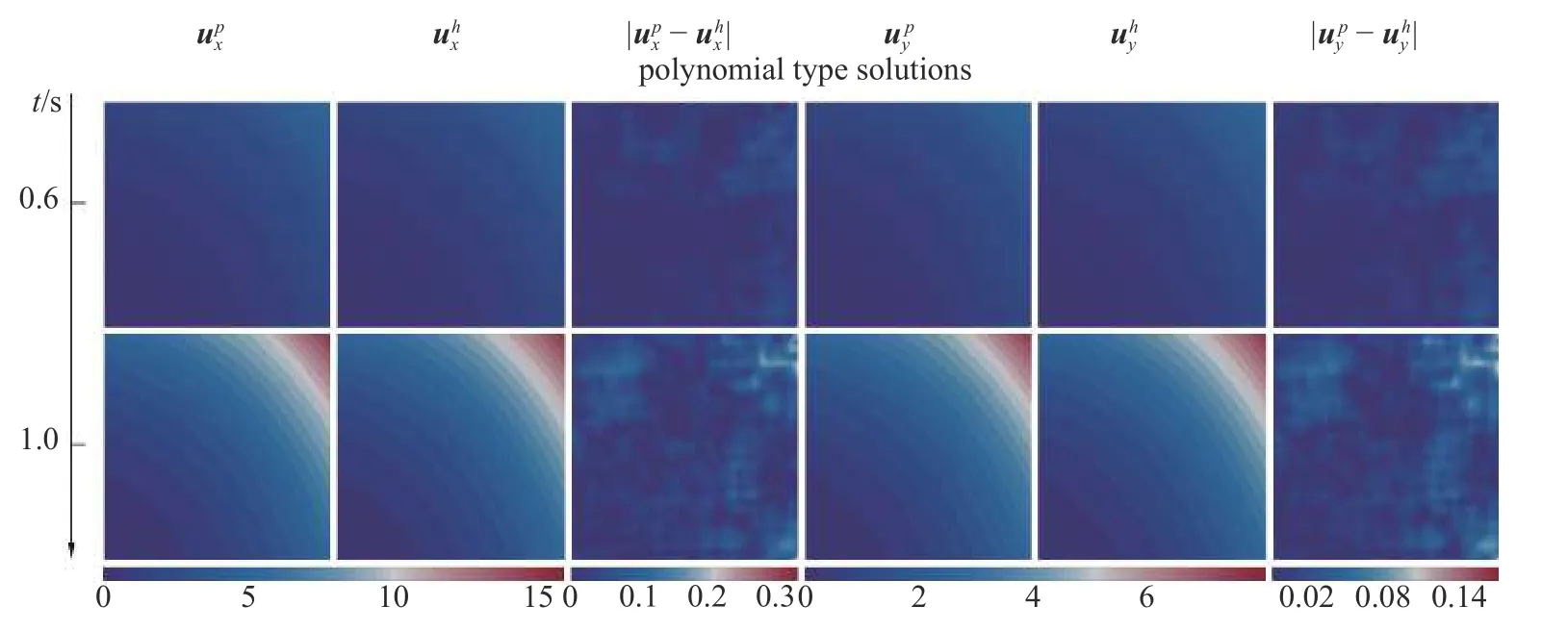
图9 方形区域弹性力学问题代理模型预测解与无网格数值解对比Fig.9 Comparison between the predicted solution of the recurrent convolution neural network surrogate model and the meshless numerical solution of the elasticity problem in the square region

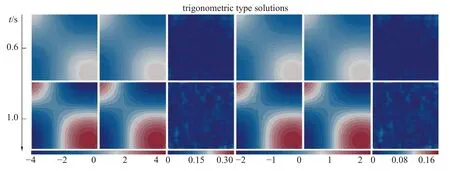
图9 方形区域弹性力学问题代理模型预测解与无网格数值解对比(续)Fig.9 Comparison between the predicted solution of the recurrent convolution neural network surrogate model and the meshless numerical solution of the elasticity problem in the square region (continued)

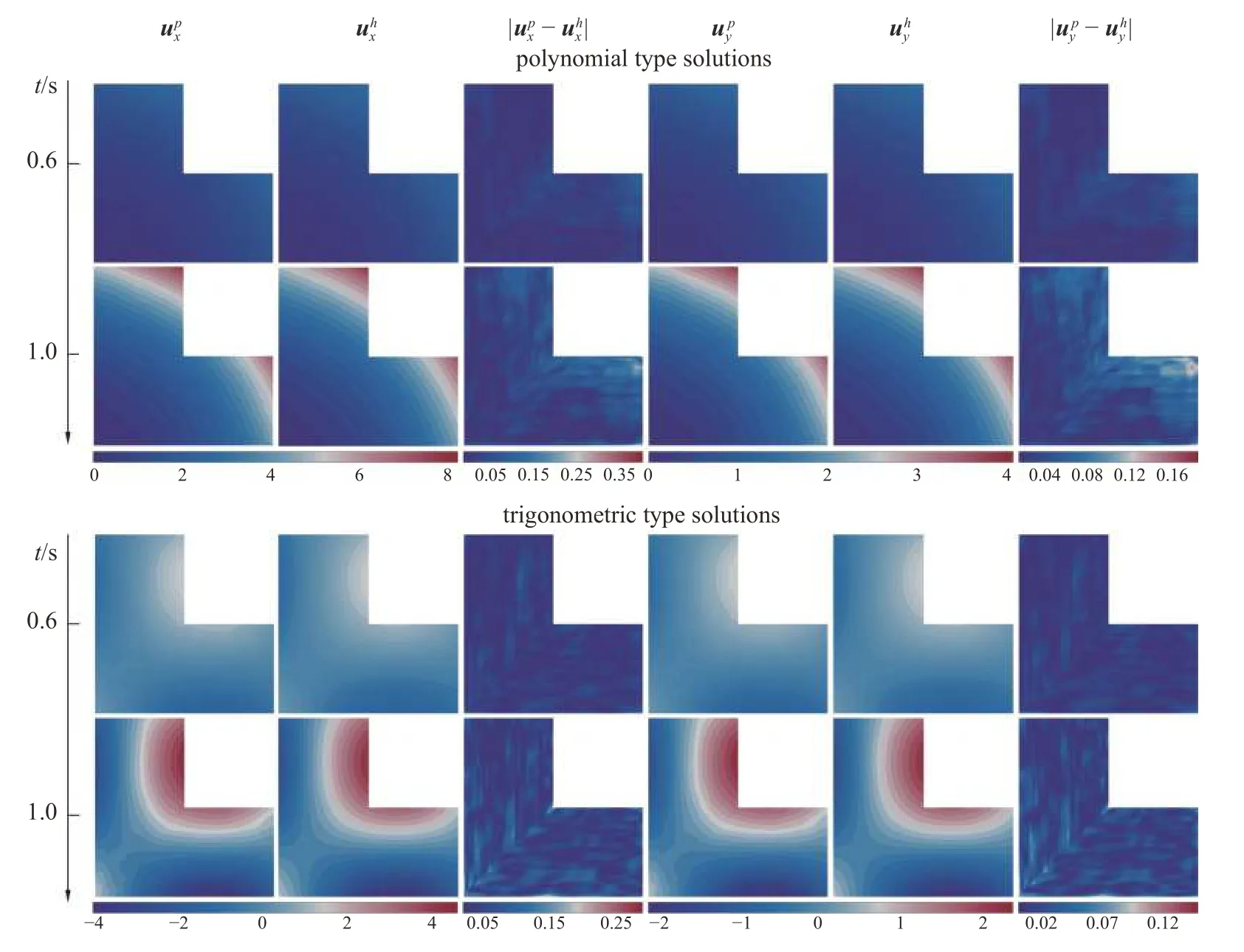
图10 L 形区域弹性力学问题代理模型预测解与无网格数值解对比Fig.10 Comparison between the predicted solution of the recurrent convolution neural network surrogate model and the meshless numerical solution of the elasticity problem in the L-shape region

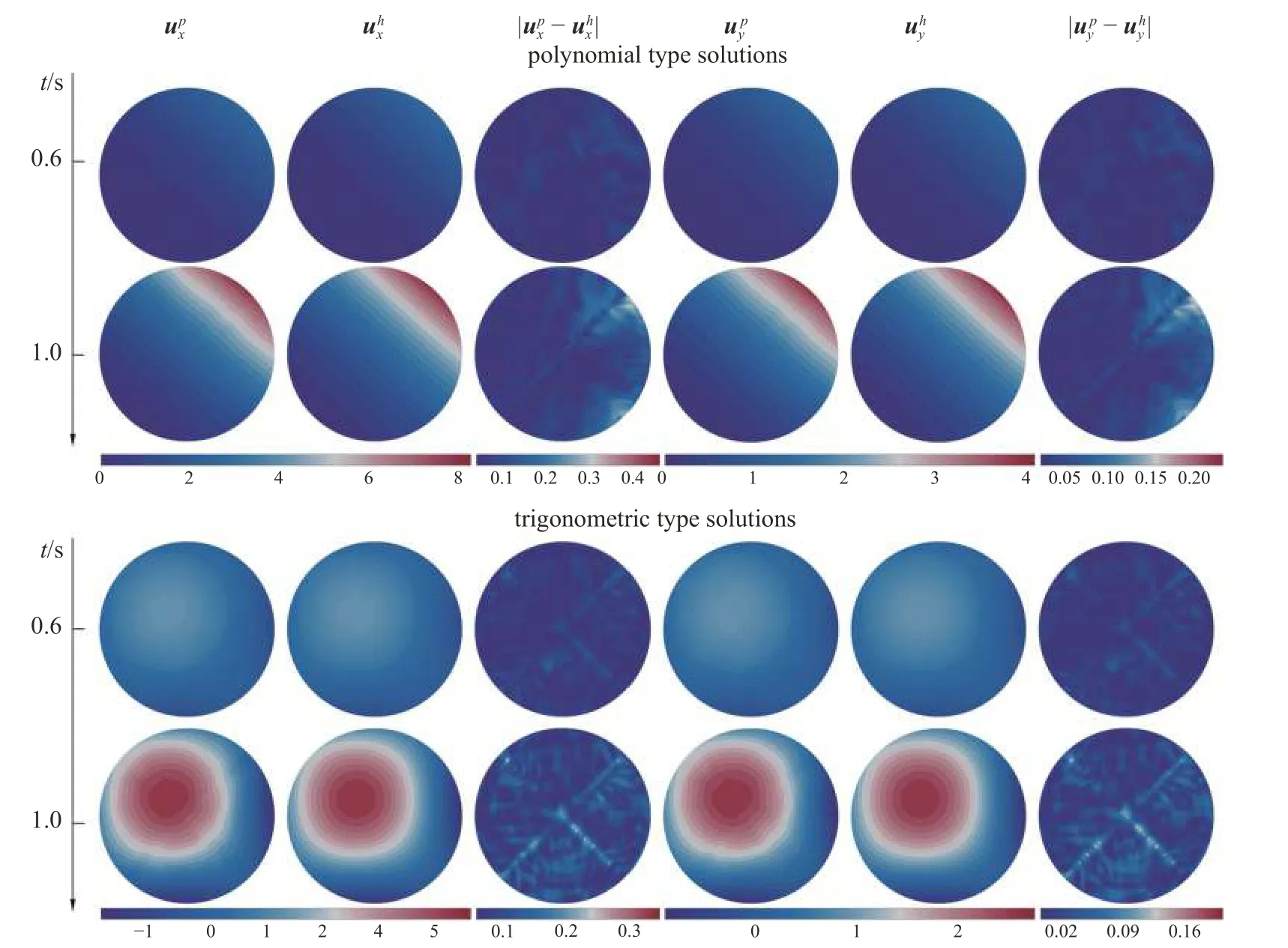
图11 圆形区域弹性力学问题代理模型预测解与无网格数值解对比Fig.11 Comparison between the predicted solution of the recurrent convolution neural network surrogate model and the meshless numerical solution of the elasticity problem in the circular region

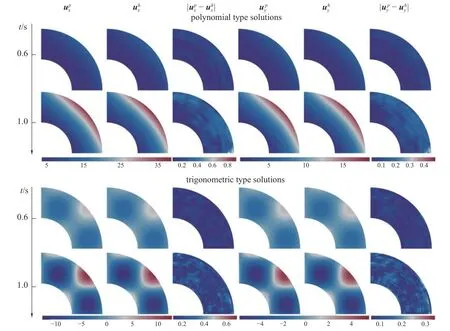
图12 四分之一环形区域弹性力学问题代理模型预测解与无网格数值解对比Fig.12 Comparison between the predicted solution of the recurrent convolution neural network surrogate model and the meshless numerical solution of the elasticity problem in the quarter annular region

表1 列出了无网格动力分析的循环卷积神经网络代理模型各个阶段的计算耗时,其中数值计算及训练数据产生使用Intel Core i5-10500 CPU 进行计算,代理模型训练及预测使用NVIDIA GeForce RTX 3060 进行计算.该代理模型的整个计算流程中包含数据集准备阶段、模型超参数训练阶段以及模型预测阶段.如表1 所示,线下准备训练集耗时占据了整个流程用时的90%以上,这也是机器学习的特征之一,即线下训练数据准备的复杂性与重要性.但当模型训练完成后,由采用代理模型与传统无网格法同时对400 组动力问题进行线上计算的所用时间比较可见,相比于传统的无网格动力分析,无网格动力分析的循环卷积神经网络代理模型可以大幅减少计算时间,显著提升计算效率.

表1 弹性问题下无网格法动力分析与循环卷积神经网络代理模型训练预测时间对比Table 1 Comparison of the training and prediction cost between dynamic meshfree analysis and recurrent convolution neural network surrogate model for elastic problems

5 结论

传统的无网格动力分析需要计算每一时间步上的结构响应,并通过循环传递到下一时间步实现整个时间域上的动力响应分析.由于无网格法形函数较为复杂,质量和刚度矩阵带宽也大于对应阶次的有限元法,因而动力分析效率较低.针对该问题,本文系统研究了无网格动力分析过程与长短期记忆神经网络学习预测过程之间存在的内在相似性和本征联系,同时充分利用无网格法在产生多样化训练样本数据方面的精度和离散灵活性优势,提出了卷积模块与循环模块并存的循环卷积神经网络作为无网格动力分析代理模型.基于无网格动力分析的循环卷积神经网络代理模型,可以高效便捷地获取任意时刻的无网格动力分析响应.文中通过4 种不同形状的弹性力学问题的数据学习,构建了相应的无网格动力分析的循环卷积神经网络代理模型.结果表明,在保证精度的情况下,本文提出的无网格动力分析的循环卷积神经网络代理模型可以大幅提高无网格动力分析的计算效率.