电磁搅拌条件下结晶器内钢液多相流动和卷渣现象的大涡模拟

李琪蓝，张立峰，陈 威，王亚栋，赵 震，张 静

1) 北京科技大学冶金与生态工程学院，北京 100083 2) 北方工业大学机械与材料工程学院，北京 100144 3) 燕山大学机械工程学院，秦皇岛 066004 4) 燕山大学车辆与能源学院，秦皇岛 066004

由于钢液的高温和不透明特性，在研究钢液流动的时候，工业测量变得非常困难，很难把连铸结晶器立体空间内的钢液流动测量出来，数值模拟仿真成为研究钢液流动的有利工具.结晶器内流动是一个复杂的物理现象，包含钢液、渣相和空气三相、高温传热且发生钢液和渣的凝固现象.关于结晶器内流动的研究自从20世纪80年代开始就得到了广泛的关注，建立的模型包括钢液单相模型、渣相-钢液或钢液-气相两相模型和空气-渣相-钢液三相模型.钢液单相模型主要应用于研究钢液流动、传热及凝固、气泡和非金属夹杂物的运动和捕获等现象.Thomas和Zhang[1]详细总结了结晶器区域内钢液流动现象的模拟研究.谭金池等[2]通过板坯结晶器三维稳态流场的计算，分析了钢液流股上下回流区的特征对流场的影响.李超与王斌[3]使用雷诺平均模拟（RANS）和大涡模拟（LES）探讨了模型对结晶器内钢液湍流流动特性的影响，在近壁处使用LES方法保证精度，在远壁处使用RANS降低计算量.Zhao等[4]通过瞬态大涡模拟和工厂试验研究了钢液的湍流流动和结晶器区域内钢液的热量传输.刘中秋等[5]研究了通过水口向结晶器钢液内吹入氩气后的非稳态湍流运动.陈威与张立峰[6]通过大涡模拟模型、凝固模型和离散相(DPM)模型的耦合计算，研究了湍流对夹杂物在结晶器内运动和去除的影响.单相模型主要用来研究钢液内部的流动现象，不能准确研究渣相和钢液界面处的物理现象.

两相模型和三相模型既可以研究钢液内部的流动现象，也可以研究渣相-钢液界面处的卷渣和渣滴的运动等现象.Anagnostopoulos与Bergeles[7]通过对比水-油模型的测量结果和渣相-钢液两相模型的计算结果，研究了流速和水口浸入深度对结晶器钢渣界面形状的变化.王军等[8]利用VOF多相流模型和Lagrangian离散相模型模拟了钢-渣界面的波动行为和界面形状.Sun等[9]采用VOF多相流模型研究了电磁搅拌和电磁制动对板坯结晶器内钢渣界面的影响.刘中秋等[10]基于k-ε湍流模型和VOF两相流模型对板坯连铸结晶器内的钢-渣界面的非稳态波动进行了研究.Chen等[11]耦合了LES模型、VOF多相流模型和离散相模型，在钢液-空气两相模型的基础上以离散相的方式注入氩气泡，研究了结晶器中钢液和弯月面的流动以及气泡分布.Wang与Zhang[12]研究了局部电磁制动对板坯连铸坯结晶器中渣相-钢液两相模型中流体流动、传热、夹杂物运动和氩气泡运动的影响.Chen等[13]建立了大涡模拟模型和VOF渣相-钢液两相流模型，通过用户自定义函数（UDF）计算了钢液中卷入渣滴的数量、大小、速度和概率，提出了卷入渣滴当量直径的分布公式.Zhang等[14]通过VOF模型和k-ε模型模拟了空气-渣相-钢液三相的流场、凝固和弯月面的现象.卢春晓等[15]耦合计算了空气-渣相-钢液三相的流动、传热与凝固，研究了板坯结晶器内弯月面处液态保护渣的流动行为.王林杰等[16]建立了方坯连铸结晶器内空气-渣相-钢液三相的三维流动、传热与凝固的耦合模型，研究了结晶器内钢液的瞬态流动及其对弯月面液面波动和保护渣流动的影响.

上述研究主要是研究结晶器内钢液的流动、传热、凝固或者夹杂物行为，有的也模拟了结晶器表面钢-渣两相界面的形状.对于渣滴从钢-渣界面处扭曲、撕裂和脱落然后进入钢液的运动行为的模拟仿真还不成熟.此外，在模拟钢液单相流动或者钢渣两相流动时，一般都假设渣相上面没有空气相，即计算域的上表面是平的，这会造成能量在计算域的顶部无法有效耗散，进而导致临近计算域顶面附近区域的流动比实际要剧烈、湍动能比实际要高.所以本文的研究对比了结晶器内钢液单相流动、渣相-钢液两相、空气-渣相-钢液三相的多相流动.

只有能够模拟各向异性流动的非稳态湍流模型才能模拟结晶器钢液面的卷渣行为，例如雷诺应力模型(Reynolds stress model)[20-21]和大涡模拟模型 (Large eddy simulation，即 LES)[15,22-27].本文的研究使用LES湍流模型来模拟结晶器钢液面的卷渣行为.

结晶器电磁搅拌在钢的连铸过程中被广泛应用，电磁搅拌对钢质量有利影响的报道已经很多[28-32].文献[33-34]指出，电磁搅拌可以显著减少皮下夹杂物和皮下气泡.但是，结晶器位置强烈的电磁搅拌必然会加剧钢液面的波动进而导致卷渣的发生，关于结晶器电磁搅拌对钢-渣界面卷渣的定量影响的模拟仿真还鲜有报道.

结晶器内钢液存在传热和凝固现象，关于结晶器内由传热引起的温度梯度对钢液流动产生的热浮力的影响已有研究进行了详细讨论[1,35-37].Lan[35]等得出了在钢包更换过程中，结晶器液相区范围由于受到热浮力的明显影响而会发生沿轴向缩小、沿径向扩大的结论.但是，此文中采用的钢液热膨胀系数为10-3K-1，比钢液实际的热膨胀系数大10倍，所以模拟结果和实际肯定不符合[36-37]，所以，此文错误的得出了热浮力明显影响结晶器内钢液流动的结论.Thomas和Zhang[1]的研究指出，热浮力对钢液流动的影响在结晶器内钢液的不同区域内是不同的：热浮力对钢液流动的影响主要在结晶器流股下方即强制流动较弱的区域，而在结晶器上部钢液的流动主要由浸入式水口射流引起的强制流动来驱动，所以，热浮力对钢-渣界面流动的影响是可以忽略的[1,36].结晶器电磁搅拌主要是对搅拌器所在的区域附近产生影响，且电磁力沿着连铸坯表面至中心呈现减小的趋势.弯月面处的凝固坯壳非常薄，仅仅会对铜板与钢液相和渣相接触的三相接触线处的流动速度有一定的影响，而对于三相接触线之外的钢渣界面上的流动不会产生很大的影响[38].本文主要研究钢渣界面处的卷渣行为，所以忽略了传热和凝固的影响.

本研究利用LES模型模拟湍流，利用VOF模型模拟多相流，分别研究了结晶器内钢液单相模型、渣相-钢液两相模型和空气-渣相-钢液三相模型3种情况下的三维瞬态流场分布、钢-渣界面液位波动和卷渣的现象，并讨论了结晶器电磁搅拌对卷渣的定量影响.

1 数学模型

1.1 电磁场控制方程

由于本研究中电磁场频率较低，故在讨论电磁作用的影响时，忽略了位移电流的影响[39-41]，在描述计算域中每一点的电磁场关系时，可通过简化的麦克斯韦方程组，式(1)～(4)，和媒质的本构关系式，式(5)～(7)求解：

式中：r为哈密尔顿算子，是某一物理量在空间三个坐标方向的偏导数的矢量和；H为磁场强度，A·m-1；E为电场强度，V·m-1；D为电通密度，C·m-2；B为磁通密度，T；J为电流密度，A·m-2；t为时间，s；ρV为电荷密度，C·m-3；ε为介电常数，C2·N-1·m-2；µ为磁导率，H·m-1；σ为电导率，S·m-1.

当求解分析谐波电磁场时，电磁力被分解为时间平均电磁力和脉动电磁力.在耦合计算过程中采用了时间平均洛伦兹力[39,41]，其表达式如下：

式中：Fmag为洛伦兹力，N；B*为B的共轭复数，Re为共轭复数的实部.在本研究中电磁场对多相流动的影响通过在动量方程加入电磁力源项来实现.

1.2 湍流流动控制方程

VOF多相流模型条件下的连续性方程为

式中，αq和uq分别为第q相的体积分数和速度.

在多相流动中，第q相的动量方程为：

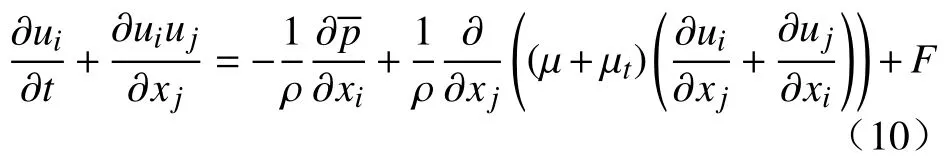
式中，F为电磁力源项，将X、Y两个方向的电磁力通过用户自定义函数（User defined function，UDF）加载到动量方程中.在搅拌电流为150 A、频率为2 Hz条件下的电磁力表达式如式(11)和(12)所示.

式中，FX和FY分别为X、Y方向的电磁力，N·m-3；X、Y、Z分别为宽度方向、厚度方向和拉坯方向的坐标，m.

大涡模拟湍流模型的基本原理是使用滤波函数分离大尺度脉动和小尺度脉动，对大尺度的大涡结构进行直接数值模拟求解，对小尺度湍流构造亚格子模型求解.相比于雷诺平均模拟，该模型可以更好地分辨在不同方向上各向异性的湍流，能够捕捉流场的非稳态信息.本研究采用Smargorinsky-Lilly[42]涡黏模式计算亚格子涡黏性系数，其计算方程如下：

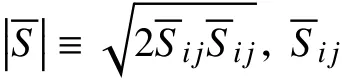
式中：κ为von Kármán常数；d为到最近的壁面的距离，m；CS为Smargorinsky常数，取0.18；V为计算单元的体积，m3.

1.3 计算域及网格

基于国内某厂的280 mm×250 mm大方坯连铸结晶器内的多相流动现象进行模拟研究，由于钢-渣液面运动剧烈，为了更加准确地捕获液位波动和卷渣，对钢-渣交界处的网格进行了细化处理.三相模型的计算域和局部网格设置如图1所示.模型包括直通式浸入式水口（水口浸入深度120 mm）、连铸机结晶器（顶部空气相高度为65 mm、渣相高度为35 mm）和部分二冷区.连铸机浇铸半径为10.25 m，具体模型尺寸和物性参数如表1所示.两相模型和单相模型在三相模型的基础上，分别省略了空气相和渣相.计算域总体积0.112～0.119 m3，网格数为33.5万～38.3万.

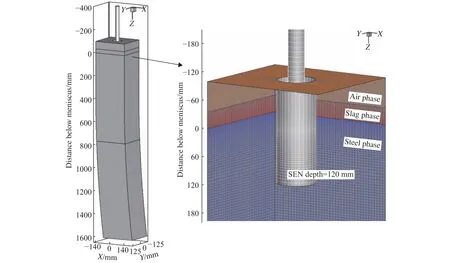
图1 空气-渣相-钢液三相模型的物理模型尺寸和网格设置Fig.1 Schematic of physical model size and mesh distribution of the steel-slag-air three-phase model

表1 模型尺寸及物性参数Table 1 Model dimensions and material parameters

电磁搅拌的安装位置如图2(a)所示.图2(b)显示了沿结晶器中心线上磁感应强度分布的计算值与使用高斯仪空载测量的测量值之间的对比.电磁感应强度沿拉坯方向先增大后减小，并在距离结晶器顶面700 mm左右处达到最大值.计算值与测量值基本吻合，进而验证了结晶器电磁搅拌模型的准确性.图3为结晶器垂直中心线上的电磁力分布，可以看出，改变电流强度大小和频率大小，结晶器内钢液受到的电磁力大小发生变化，电磁力随电流强度增大而增大，随电流频率增大而减小.由于Z方向上的电磁力远小于X、Y方向的电磁力，故可以忽略.

图2 电磁搅拌位置示意图及模型验证.(a) 电磁搅拌安装位置示意图; (b) 结晶器中心线处磁通密度测量值与计算值的对比Fig.2 Diagram of the M-EMS installing location and model validation: (a) M-EMS installing location; (b) magnetic flux density along the mold center vertical direction

图3 结晶器垂直中心线上的电磁力分布Fig.3 Distribution of the electromagnetic force along the vertical distance below the meniscus

1.4 边界条件

浸入式水口入口处采用速度入口边界条件，其速度大小根据质量守恒由拉速和连铸坯断面尺寸和钢液密度确定.计算域结晶器最上部采用自由边界条件，表面剪切力为零.计算域出口采用压力出口条件，回流温度通过设置UDF实现[12].其余壁面均采用无滑移边界条件.

本研究通过商业软件ANSYS FLUENT 17.0并UDF对以上方程进行求解，求解方法采用非迭代时间推进法(Non-iterative time advance)，压力-速度耦合采用PISO 算法，能量方程的离散采用的是二阶隐式格式.控制方程中的连续性和动量方程的计算残差控制在0.001以下.模拟计算的时间步长为0.005 s，结晶器内多相流动计算至110.0 s基本稳定后，取随后的30 s内的计算值进行时均处理.在32核64线程的计算机上，三相模型、两相模型和单相模型的运行时间分别为177、71和35 h.

2 结晶器钢液多相流动、液位波动与卷渣

图4显示了不同模型下钢液的时均速度分布，由于电磁搅拌作用加快了钢液的流动，钢液从浸入式水口射出后在结晶器电磁搅拌器附近的流动速度更大.整体而言，结晶器内钢液的速度分布在目前3种模型下差别不大.

图4 时均速度大小分布.(a)钢液单相模型; (b)渣相-钢液两相模型;(c)空气-渣相-钢液三相模型Fig.4 Distribution of time-average velocity magnitude: (a) steel-slag single-phase model; (b) steel-slag two-phase model; (c) steel-slag-air three-phase model

本文监测了钢液单相模型中P点（钢液面以下5 mm、厚度中心、宽度1/4）处钢液沿X、Y、Z3个方向的脉动速度，如图5所示.可以看出，3个方向的脉动速度值明显不同.P点处钢液沿X、Y、Z脉动速度绝对值的平均大小分别为0.020、0.029和0.012 m·s-1.因此，“各向同性”的k-ε湍流模型本质上是不能正确模拟结晶器内的非稳态湍流流动的，LES模型可以用来模拟结晶器内的非稳态湍流流动.

图5 监测点P点处钢液3个方向上的脉动速度Fig.5 Steel fluctuation velocity in different directions at monitored point P

对于钢液单相模型来说，可通过简单的势能关系，即式（15）估算钢液顶面的液面位置（Δz）[43]来近似描述 “弯月面”的形状.

式中：P(x,y)和Pmean分别为顶面各坐标点处的压力和整个顶面的平均压力，Pa；ρsteel和ρslag分别为钢液和渣的密度，kg·m-3；g为重力加速度，9.8 m·s-2.

对于渣相-钢液两相流动和空气-渣相-钢液三相流动行为，假定钢液体积分数（fsteel）为0.9的等值面为钢-渣界面，即钢液表面的弯月面.

图6显示了3个模型条件下弯月面的三维轮廓、时均速度分布及其中心线上的速度大小的定量结果.弯月面都呈现壁面处液位较高而中心处液位较低的液面形状.单相模型、两相模型和三相模型下弯月面的最大速度分别为0.227、0.166和0.168 m·s-1，整体平均时均速度分别为0.1373、0.0976和0.1029 m·s-1.两相模型与三相模型的平均时均速度非常接近，而单相模型较两相模型和三相模型的平均时均速度分别增大了40.67%、33.43%，这是因为渣相覆盖在钢液上层对钢液的流动产生了抑制效果，故多相模型预测得到的弯月面钢液速度较单相模型小.因此，钢液上表面的物相存在状态对钢液表面的速度产生了较为明显的影响.

图6 弯月面时均速度分布.(a)钢液单相模型; (b)渣相-钢液两相模型; (c)空气-渣相-钢液三相模型; (d) 弯月面在结晶器厚度中心线上的流动的速度大小Fig.6 Time-average speed distribution of the meniscus: (a) steel-slag single-phase model; (b) steel-slag two-phase model; (c) steel-slag-air three-phase model; (d) time-average velocity magnitude along meniscus width center line

由于钢液单相模型不涉及钢-渣液面波动和卷渣现象，本小节只对比讨论渣相-钢液两相模型和空气-渣相-钢液三相模型.如图7所示，本文沿着结晶器宽面中心线和窄面中心线，分别在距离浸入式水口外壁 4 mm处（P1、P4）、1/4断面处（P2、P5）、距离结晶器壁面 5 mm 处（P3、P6）的液位分布进行了实时监测.

图7 液位监测点Fig.7 Monitoring points of the surface level

图8为结晶器宽面中心面靠近水口P1点和结晶器壁面处P3点的液位波动分布.本文首先使用Savitzky-Golay滤波方法[44-45]对监测点的液位进行了平滑处理，然后使用原始液位减去平滑后的数据来计算液位波动值[45-46].由于结晶器电磁搅拌器安装在结晶器下部靠近出口的位置，整体液面波动并不剧烈，在150 A、2 Hz的电磁搅拌条件下液面波动范围在±5 mm内.由图8可见，两相模型和三相模型靠近水口处的液位波动最大值分别为3.6和1.9 mm，靠近结晶器壁面处的液面波动最大值分别为3.0和0.4 mm.即靠近水口处液位波动较靠近结晶器壁面处更加剧烈，且两相模型计算得到的液位波动较三相模型也更加剧烈.

图8 不同监测点处的液面波动.(a) P1; (b) P3Fig.8 Surface fluctuations at different monitoring points: (a) P1; (b) P3

由于在目前工况下的卷渣程度较轻，很难通过数值模拟结果直接显示卷渣程度的差异，本研究通过卷渣速率[15]来定量评估卷渣的剧烈程度，卷渣速率的定义为：

图9为通过钢液顶面下方40 mm处即Z=0.04 m平面的渣相质量随时间的变化曲线，曲线的斜率就是卷渣速率.在电流强度为150 A、电流频率为2 Hz的电磁搅拌条件下，两相模型与三相模型通过Z=0.04 m平面的卷渣速率分别为0.00118和0.00040 kg·s-1.渣相-钢液两相模型的卷渣速率明显大于空气-渣相-钢液三相模型的卷渣速率，即两相模型预测的卷渣比三相模型更加剧烈.

图9 通过Z=0.04 m平面的净渣相质量Fig.9 Net slag mass through the horizontal plane of Z=0.04 m below the mold top surface

湍动能是用来表征湍流的参数之一，本文根据湍动能的定义式（18）[47-48]来计算大涡模拟模型计算下的湍动能分布.

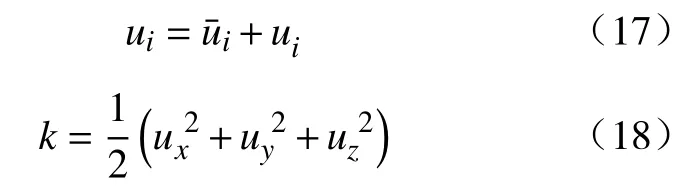
式中，ui，i和ui′分别为x、y、z3 个方向上的瞬时速度，平均速度和脉动速度，m·s-1；k为湍动能，m2·s-2.

钢-渣界面处的湍动能分布如图10所示，两相模型下钢-渣界面的湍动能明显大于三相模型.钢-渣界面宽度中心线的液位轮廓和湍动能数值如图11所示.可以看出两相模型的液面较三相模型稍微平缓，靠近壁面处两相模型的液位略低于三相模型，而靠近水口处两相模型的液位略高于三相模型.两相模型和三相模型钢-渣界面的湍动能最大值均出现在水口附近和结晶器壁面附近，平均湍动能分别为0.00110和0.00074 m2·s-2.可以看出，渣相-钢液两相模型条件下，计算得到的钢-渣界面处的湍动能偏大，因此造成预测的卷渣速率偏大.

图10 钢-渣界面的湍动能分布.(a) 渣相-钢液两相模型; (b) 空气-渣相-钢液三项模型Fig.10 Turbulence kinetic energy distribution on steel/slag interface: (a) steel-slag two-phase model; (b) steel-slag-air three-phase model

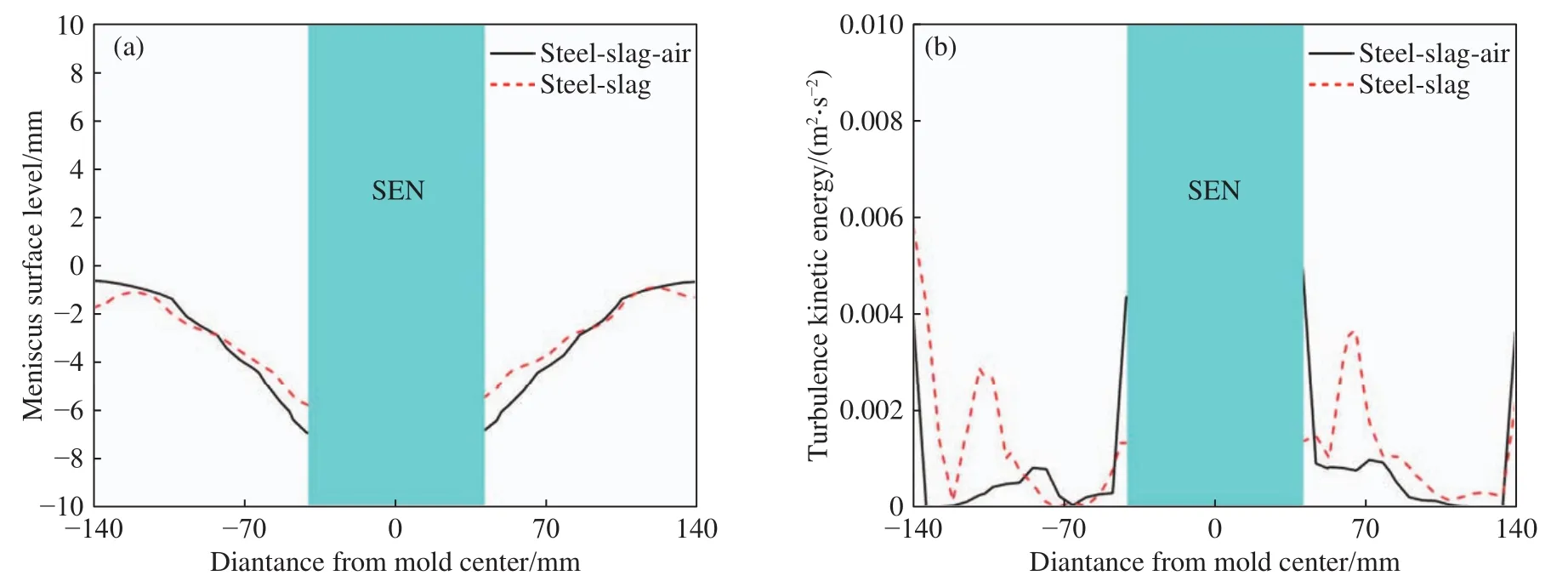
图11 钢-渣界面宽度中心线.(a) 液面瞬时位置; (b) 湍动能值Fig.11 Along steel/slag interface: (a) surface transient level position; (b) turbulence kinetic energy

3 电磁搅拌参数对卷渣的定量影响

3.1 搅拌电流大小

电流为300 A、频率为2 Hz电磁搅拌条件下弯月面的时均速度如图12所示.单相、两相和三相模型弯月面的整体平均时均速度分别为0.2519、0.1987和0.2000 m·s-1.与电流为150 A、频率为2 Hz条件下的规律相同，两相模型与三相模型的平均时均速度相近，而单相模型的平均时均速度较其分别增大了26.8%和24.6%.相比于电流150 A、频率2 Hz电磁搅拌下的弯月面速度分布，电流强度的增大使得电磁搅拌作用增强，钢液电磁力增大，弯月面的平均时均速度也明显增大.

图12 电流300 A,频率 2 Hz的电磁搅拌条件下弯月面宽度中心线处时均速度Fig.12 Time-average velocity magnitude along meniscus width center line

图13为电磁频率为2 Hz，电流强度分别为150和300 A时通过结晶器顶面以下0.04 m平面的净卷渣质量.300 A条件下两相模型和三相模型的卷渣速率分别为0.00600和0.00578 kg·s-1.随着电流强度的增大，卷渣速率增大.这说明有更多的渣被持续卷入结晶器钢液中，被凝固坯壳捕获后会形成连铸坯的内部缺陷.

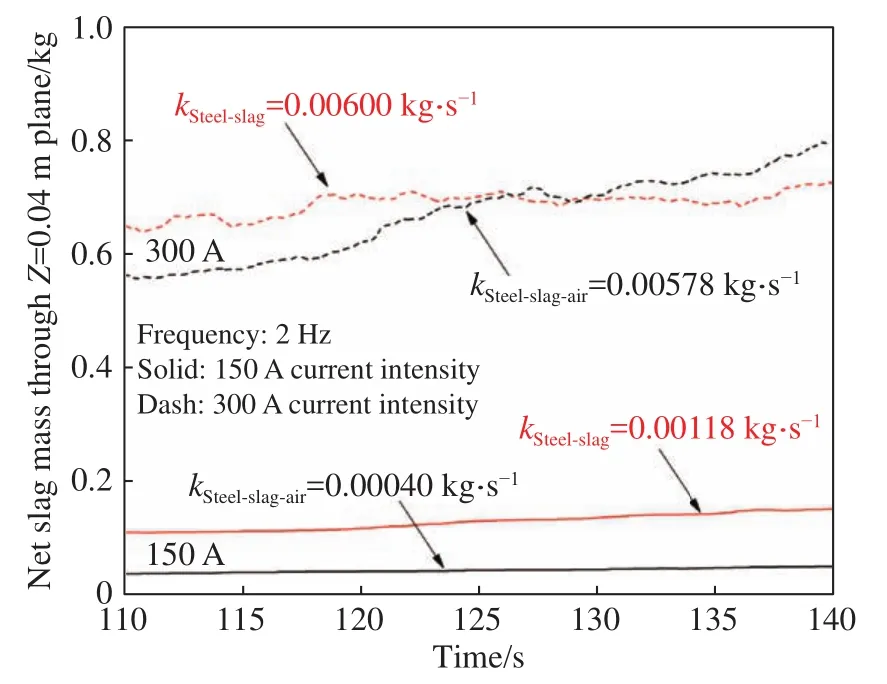
图13 不同电流强度下通过Z=0.04 m平面的净渣相质量Fig.13 Net slag mass through the horizontal plane of Z=0.04 m below mold top surface under different current densities

3.2 搅拌电流的频率

图14为电流150 A、频率4 Hz电磁搅拌条件下弯月面的时均速度分布.单相、两相、三相模型弯月面的整体平均时均速度分别为0.0992、0.0688和0.0725 m·s-1.单相模型较两相模型和三相模型的平均时均速度分别增大了44.19%和36.83%.相比于电流150 A、频率2 Hz的电磁搅拌（图12），随着电流频率的增大，磁感应强度减小，钢液所受电磁力减小，这导致弯月面的平均时均速度明显减小.

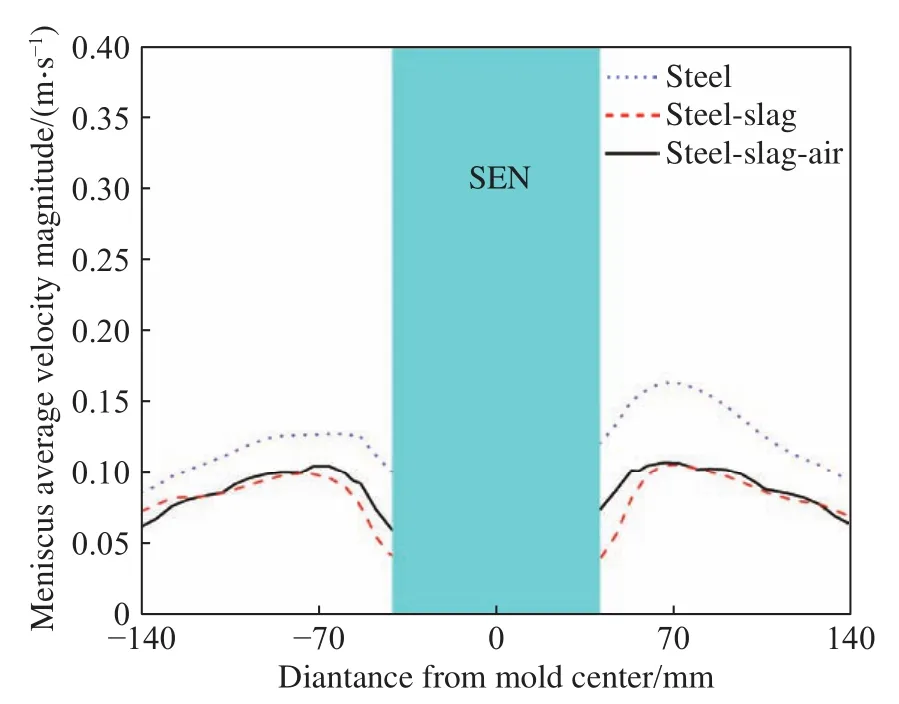
图14 150 A, 4 Hz下弯月面宽度中心线处时均速度大小Fig.14 Time-average velocity magnitude along meniscus width center line under 150 A current intensity and 2 Hz frequency

如图15所示，保持电流强度为150 A，当电磁搅拌频率增大到4 Hz时两相模型和三相模型的卷渣速率分别为0.00121和0.00014 kg·s-1，相较于频率为2 Hz时，两相模型的卷渣速率差别不大，而三相模型的卷渣速率明显减小.

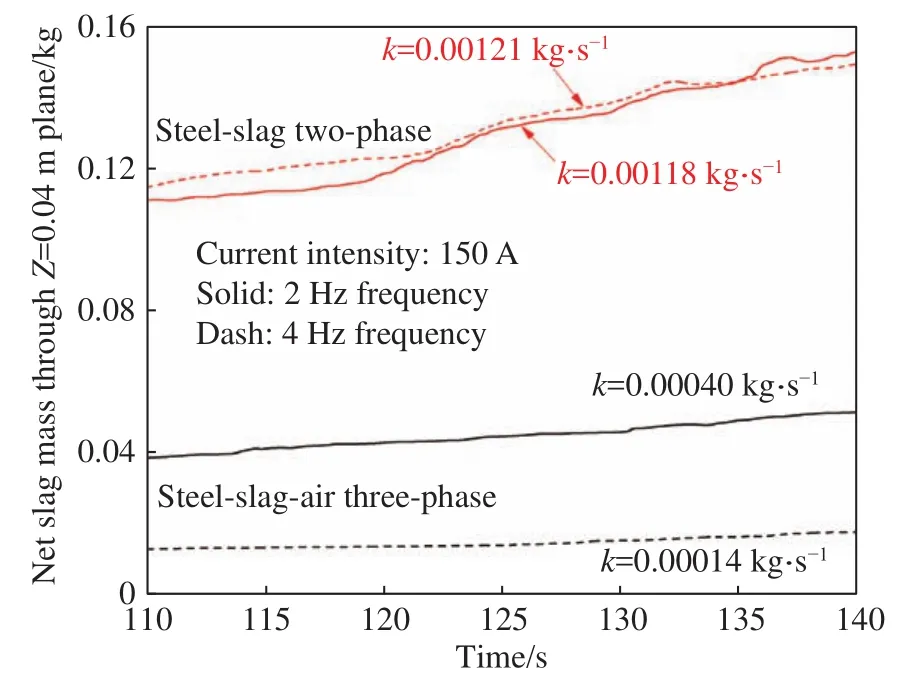
图15 不同电流频率下通过Z=0.04 m平面的净渣相质量Fig.15 Net slag mass through the horizontal plane of Z=0.04 m below mold top surface under different current frequency

综合以上结果，当搅拌电流强度增大到300 A时，渣相-钢液两相模型和空气-渣相-钢液三相模型的卷渣速率分别为150 A条件下的5倍和15倍；当电流频率增大到4 Hz时，渣相-钢液两相模型的卷渣速率变化很小，空气-渣相-钢液三相模型的卷渣速率降低为2 Hz条件下的1/3.改变电磁搅拌参数对三相模型的卷渣速率影响更大，这说明在模拟有M-EMS条件下结晶器内的卷渣现象时，应选择空气-渣相-钢液三相模型更为准确.

4 连铸坯中卷渣类夹杂物的工业 CT 检测

基于已有研究的对连铸坯内部质量的工业CT检测经验[49]，采用高分辨率微焦点CT系统对连铸坯内部的缺陷进行了扫描，假设球形度大于0.6的缺陷为卷渣类夹杂物缺陷.将连铸坯距离外弧不同位置处切割出7 mm×7 mm×10 mm的样品分别送入X-CT设备（YXLON FF35 CT），在200 kV加速电压、120 μA束流的条件下放大20倍后进行检测.结晶器使用不同搅拌电流强度条件下的连铸坯皮下卷渣类大颗粒夹杂物的形貌示于图16.

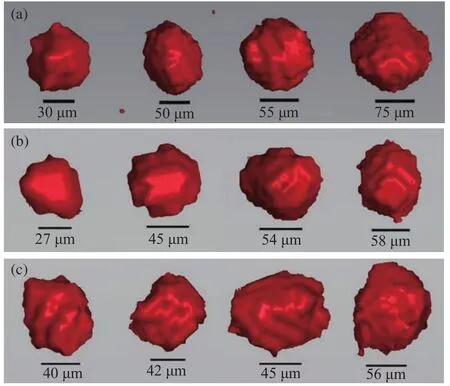
图16 不同电流强度下的夹杂物形貌.(a) 100 A; (b) 300 A; (c) 600 AFig.16 Morphologies of slag entrainment inclusions with M-EMS of different current intensities: (a) 100 A; (b) 300 A; (c) 600 A

图17为不同电流强度下卷渣类夹杂物的体积分数.可以看出，随着电流强度的增大，卷渣类夹杂物的体积分数也增大.这是由于电流强度的增大加强了电磁搅拌的搅拌强度，导致卷渣带入的大颗粒夹杂物数量增多.所以，结晶器电磁搅拌过于剧烈会导致卷渣过多，连铸坯的夹渣类缺陷更加严重.以上3种不同模型结果表明改变电磁搅拌参数对三相模型的卷渣速率影响更大，这与不同电磁搅拌参数下CT检测结果变化相一致.因此，在模拟有结晶器电磁搅拌情况下结晶器内的卷渣现象时应该选择空气-渣相-钢液三相模型更为准确.

图17 不同电流强度下卷渣类夹杂物的体积分数Fig.17 Volume fraction of inclusions from slag entrainment in the CC bloom varied with different current intensities M-EMS

5 结论

（1）3种模型条件下，结晶器钢液内部的流动差别较小，但是在钢-渣界面处的行为差别较大；与其他两种多相模型相比，钢液单相模型的顶面速度明显较大，平均速度为0.1373 m·s-1，渣相-钢液两相时钢渣界面的平均速度为0.0976 m·s-1，平均湍动能为0.00110 m2·s-2，空气-渣相-钢液三相时渣钢界面的平均速度为0.1029 m·s-1，平均湍动能为0.00074 m2·s-2.

（2）弯月面靠近水口处的液面波动比靠近结晶器壁面处更加剧烈，渣相-钢液两相模型的计算结果比空气-渣相-钢液三相模型下的液面波动更为剧烈，渣相-钢液两相时水口处的液面波动最大达到3.6 mm，空气-渣相-钢液三相时最大达到1.9 mm.

（3）在电流150 A、频率2 Hz的结晶器电磁搅拌下，渣相-钢液模型和空气-渣相-钢液三相模型的卷渣速率分别为0.00118和0.00040 kg·s-1.在模拟或预测结晶器钢-渣界面的卷渣时，如果应用渣相-钢液两相模型，因为渣的上表面已经固定为平面，无法产生波动变化；即渣相上表面由于波动而耗散的能量改变为在钢-渣界面处发生扰动，所以会造成卷渣速率偏大；在预测结晶器钢-渣界面的卷渣时必须使用空气-渣相-钢液三相进行模拟.

（4）在频率为2 Hz的搅拌条件下，搅拌电流强度从150增大到300 A，渣相-钢液两相模型的卷渣速率增大到0.00600 kg·s-1，空气-渣相-钢液三相模型的卷渣速率达到0.00578 kg·s-1；在150 A搅拌电流情况下，搅拌频率从2 Hz增大到4 Hz，渣相-钢液两相模型的卷渣速率略微增大为0.00121 kg·s-1，空气-渣相-钢液三相模型的卷渣速率减小为0.00014 kg·s-1.结晶器钢-渣界面卷渣随着结晶器电磁搅拌的电流增大和频率降低而增大，且改变电磁搅拌参数对三相模型的卷渣速率影响更大.

（5）通过工业CT检测发现，连铸坯内卷渣类夹杂物的体积分数随电磁搅拌电流强度的增大而增大，而三相模型随电磁搅拌参数变化更明显，因此应选择三相模型进行卷渣预测.

致谢

感谢燕山大学高钢中心（HSC），河北省先进制造用高品质钢铁材料制备与应用技术创新中心，河北省先进制造用高品质钢铁材料开发与智能制造国际联合研究中心的资助.