基于公共投放区的空面多目标攻击研究

张艳霞， 吕 辉， 孙兆雨

(1.光电控制技术重点实验室，河南 洛阳 471000； 2.中国航空工业集团公司洛阳电光设备研究所，河南 洛阳 471000；3.陆装驻洛阳地区航空军事代表室，河南 洛阳 471000)

0 引言

空面多目标攻击一次进入可同时攻击多个地面/海面目标，减少开舱次数、载机滞空时间和攻击航路，降低投弹时被探测概率，可大大提高整体作战能力。目前的多目标攻击主要实现方式有：基于智能算法进行寻优的多目标攻击模型[1]，其综合运用蚁群算法、遗传算法和粒子群算法，该算法依赖于多次迭代计算，更新时间不可控，难以直接应用于机载实时计算环境；多目标可攻击扇区瞄准法[2]，该算法实现在攻击一个指定目标的同时，能够攻击其他多个目标，适用于空战环境，但在空面攻击时效能较低。基于协同攻击区的空空作战已较为成熟[3-4]，而基于公共投放区的空面多目标攻击技术研究较少，因此，本文提出一种基于公共投放区的空面多目标攻击技术。主要方法为：某航向下，根据攻击列表顺序，依次求解列表中各目标投放区与多目标公共投放区(初始为NTB(当前列表中第一个目标)投放区)的交集，若交集满足同时攻击条件，则更新为多目标公共投放区，列表遍历完成后，得到该航向下可同时攻击的一个多目标批次，依次遍历进入航向，得到能够攻击最多目标的一个多目标攻击批次，将对应的进入点及进入航向作为攻击占位信息，同理，对攻击列表中剩余目标进行求解，直到列表中无剩余目标，即可得到多个攻击批次划分结果及对应攻击航路。

1 多目标作战场景

一次多目标攻击过程如图1所示。

图1 编队多目标攻击过程Fig.1 Process of multi-target attacks

假设本次攻击规划为图1中的5个目标，根据分配给5个目标的武器类型，计算相应的单目标投放区[5]，进而计算多目标公共投放区，可以看出T1和T2存在公共投放区，且可投放航路符合连续投弹条件，T3,T4,T5存在公共投放区，且可投放航路符合连续投弹条件，故将5个目标分为2个攻击批次。可见，公共投放区求解是一种进行多目标攻击的求解途径。

2 公共投放区模型研究

2.1 公共投放区

公共攻击区是以载机为中心的各个目标实时攻击区的公共部分，但该方法计算得到的多目标公共攻击区为不规则的立体空间，难以进行数学描述，不易用于工程应用[6]。

将攻击区从以载机为中心映射到以地面目标为中心，求得各目标的投放区，进而得到公共投放区，可更直观地完成多目标攻击过程，如图2所示。

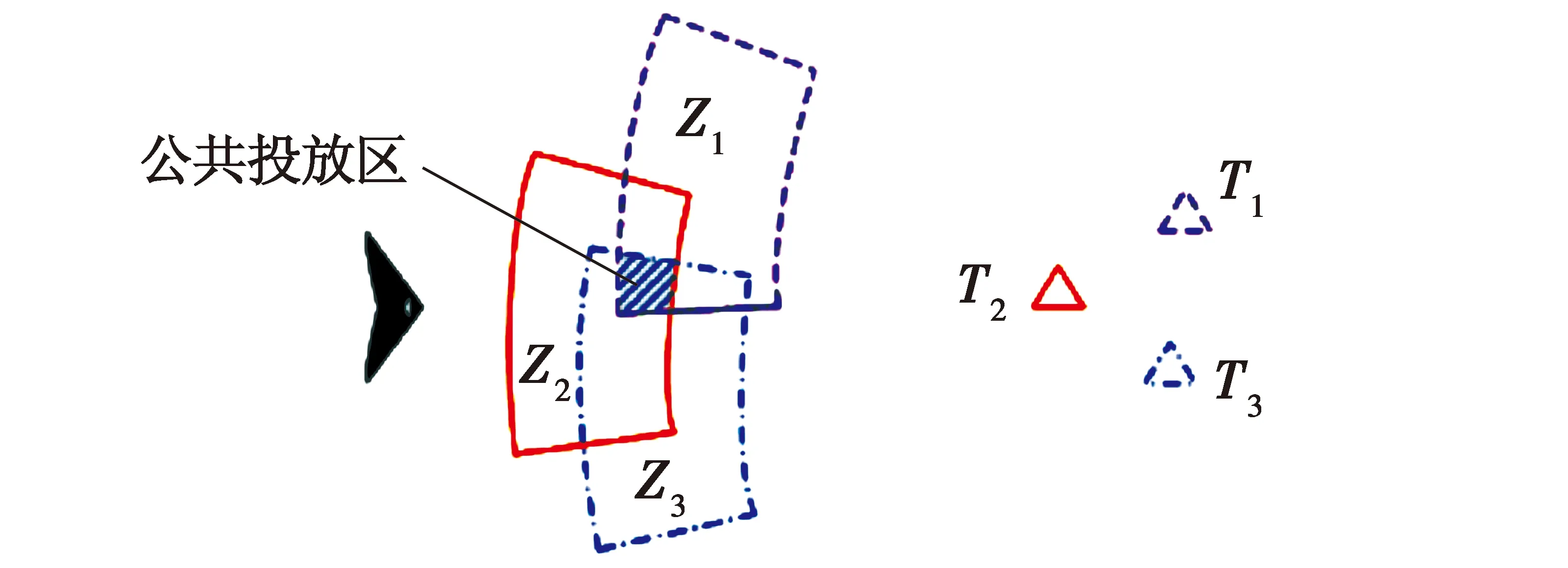
图2 多目标攻击公共投放区Fig.2 Public release zone of multi-target attacks

多目标可投放区是指在单机多目标攻击过程中，存在于预定攻击的目标集合周围的一个空间区域，载机在该区域内，只要满足投放高度、速度和姿态等约束条件，同时投放的多枚制导炸弹就能以给定精度、落角命中各自的目标，而在此区域外进行投放，就无法保证所有制导炸弹都能有效地命中目标。

2.2 公共攻击区求解模型研究

单目标投放区可以为一个多边形区域，那么公共投放区求解问题就可以看作是两个任意多边形求解问题。

以多边形1(ABCDEFGH)和多边形2(A1B1C1D1E1F1G1H1)为例说明多边形交集求解模型,如图3所示。

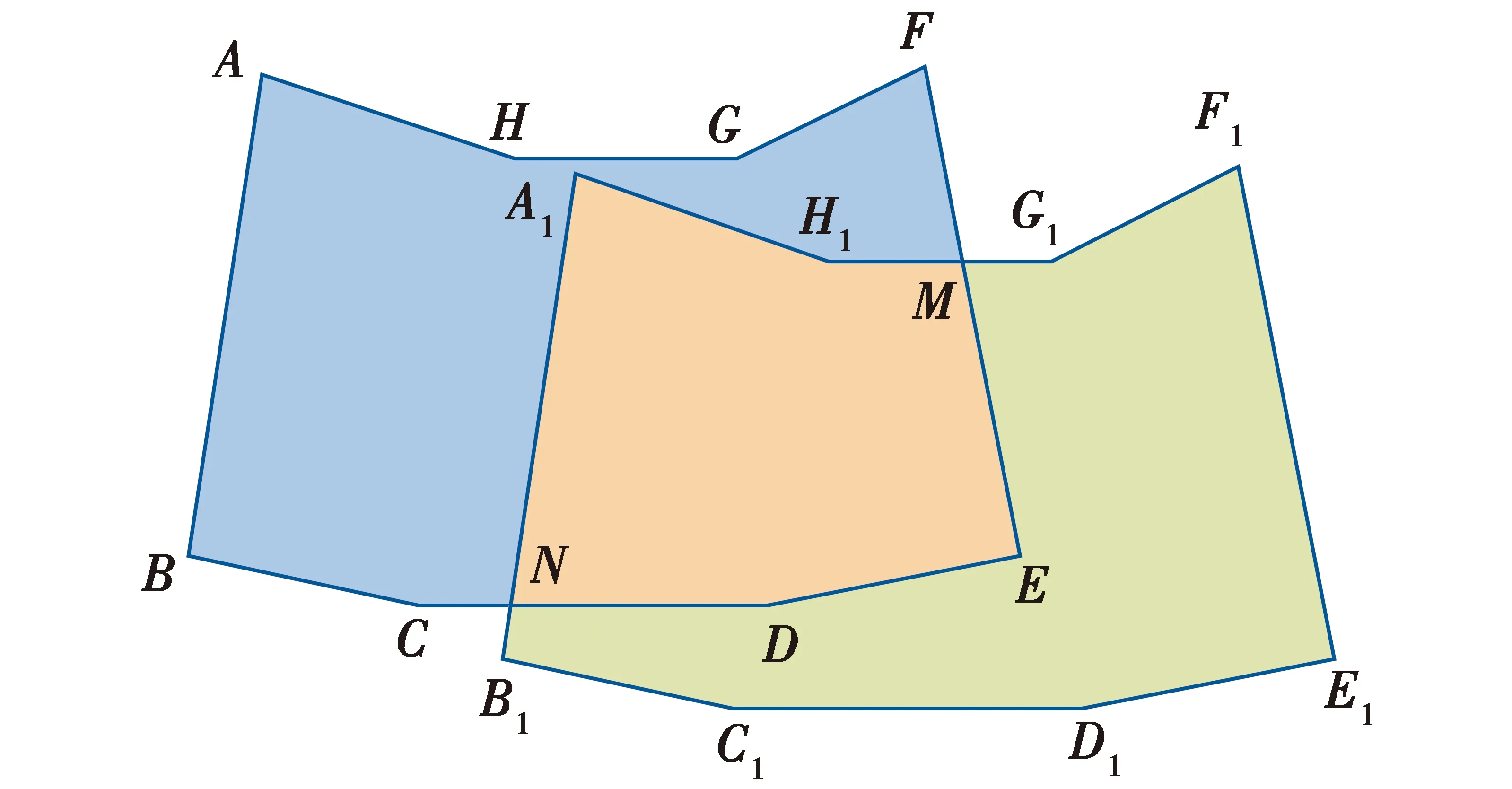
图3 多边形交集示意图Fig.3 Intersection of polygons

求解步骤如下：

1) 将两个多边形各点存储在链表中；

2) 首先遍历两个多边形各边求解的交点，若存在交点，则分别链接至对应顶点后；

3) 遍历各顶点计算公共区域，找到两个多边形公共顶点存储为交集区域的起始点，即为图中的N；

4) 求解公共投放区，从交集的表头N开始判断N和N的next1点D(在多边形1中的下一个点)的中点是否在多边形2中，若在，则链接该点，否则，改变方向，向next2点(在多边形2中的下一个点)扩展，判断M和M的next2点H1的中点是否在多边形1中，若在就继续扩展，到A1点后，A1的next2点N为起始点，多边形闭合，求解完毕。

2.3 最长攻击航路及进入点计算

假设公共投放区在NTB直角坐标系的位置如图4所示，求解进入该公共投放区的最长进入航向及对应的进入点，分为以下两种情况。

图4 最长航向计算示意图Fig.4 Calculation of heading with the longest attacking route

1) 载机航向可偏移。

在规划航路阶段，载机未进入完成该批次攻击占位，其进入点可在[Zmin,Zmax]区间内变化，求解时每隔一个ΔZ，作一条平行于X轴的直线，求解该直线与投放区的交集并从小到大排序得到交点为：x0，x1，…，x2k+1，，则对应的航路段长度为

L=L0+L1+…+Li+…+Lk

(1)

式中：

Li=x2i+1-x2i。

(2)

通过比较求得所有交线中最长的航路段长Lmax及对应的进入点坐标(x2i,z2i)及离开点坐标(x2i+1,z2i+1)。

2) 航向不可偏移。

当设定载机进入航线，在飞行航线上进行多目标攻击，此时，载机航向不可偏移，求解时，求过载机当前位置的直线z=zNTB与投放区的交集，并求解对应的最长的航路段长Lmax及对应的进入点坐标(x2 i，z2 i)及离开点坐标(x2i+1,z2i+1)。

3 多目标攻击模型研究

3.1 多目标攻击模块作战使用

多目标攻击模块与其他模块的交互关系如图5所示。

图5 多目标攻击模块与其他模块的交互关系Fig.5 Interaction between multi-targetattacking module and other modules

火控解算模块根据雷达、光雷传感器及友机、指挥中心获取的目标信息，惯导、GPS、大气机获取的载机信息，外挂获取的武器信息,以及指挥中心或长机获取的任务信息进行威胁评估，进而进行编队内目标分配，各目标攻击武器类型匹配，然后，多目标攻击模块根据当前攻击列表及匹配武器类型，进行NTB与其他目标公共投放区的解算，求解在满足攻击NTB目标的同时，兼顾攻击更多目标的目标集合及攻击进入点与最优进入航向，进而生成攻击航路，引导战斗机攻击占位[7-8]。火控解算模块将解算的多目标攻击结果、攻击航路、进入航向、攻击提示信息、攻击决策信息以及评估信息送显示器显示，在网络化复杂战场中，为飞行员提供更多、更有效的引导信息，辅助飞行员作战[9]。

3.2 多目标攻击模型研究

基于公共投放区的多目标攻击求解过程如图6所示。

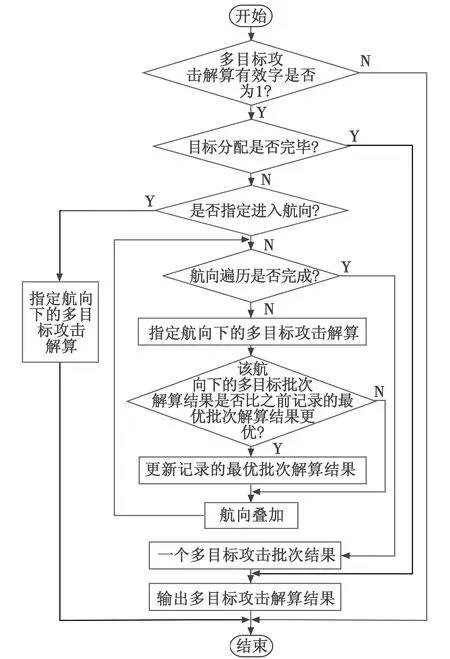
图6 多目标攻击解算流程Fig.6 Calculation of multi-target attacks

当输入的多目标攻击解算有效字为1且目标未分配完毕时，进行本次多目标攻击解算，若指定进入航向，进行该航向下的多目标攻击解算，否则，遍历进入航向，若本次航向下的多目标攻击结果比之前记录的解算结果更优(可同时攻击目标数目更多，或同样目标数目下可投放航路段更长)，更新记录的多目标解算结果，否则解算结果保持不变，航向遍历完成后，得到本次多目标解算结果，包括公共投放区信息、可同时攻击的目标数、目标编号、进入航向、进入点等。同理，依次求解剩余目标可同时攻击批次信息，直至攻击列表所有目标被分配完毕，即可得到多个攻击结果及对应攻击进入点及进入航向，引导飞行员或无人机攻击占位。

由图6可知，多目标攻击解算中的关键计算模型为指定航线下的多目标攻击解算，其解算流程如图7所示。

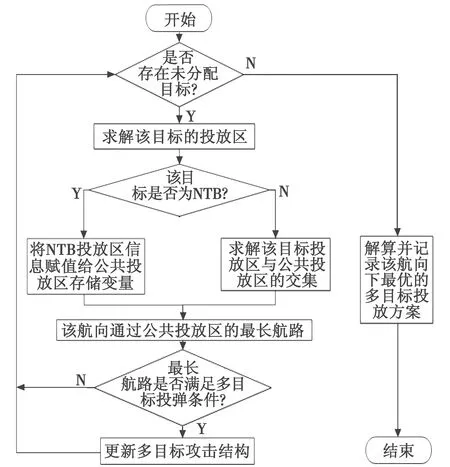
图7 指定航向下的多目标攻击解算流程Fig.7 Calculation of multi-target attacks on designated heading

首先计算NTB目标的投放区，作为公共投放区的初始解，再遍历计算非NTB目标的投放区，并将其与公共投放区进行交集运算，若交集不存在，则直接跳过该目标，若交集存在，则计算该航向通过公共投放区的最长航路，若最长航路满足多目标投弹条件，则更新计算结果，否则公共投放区保持不变；遍历完所有目标后，输出该航向下最优的多目标投放方案。

4 仿真研究

设计多目标攻击仿真软件，软件根据输入参数文件计算多目标攻击结果，并进行界面显示，验证模型设计的正确性及合理性[10]。

4.1 同种武器多目标攻击仿真(仿真1)

假设飞机携带5枚相同的卫星制导炸弹，攻击5个目标，仿真结果如图8所示。

图8 多目标攻击仿真1结果Fig.8 Multi-target attacking result of Simulation 1

图8中，红色区域为求解的公共投放区区域，蓝色线为进入航线，结果显示，本次可同时攻击5个目标以及可同时攻击的目标编号、进入航线、进入点信息等。

4.2 不同武器多目标攻击仿真(仿真2)

假设飞机携带3枚不同的制导炸弹，攻击3个目标，仿真结果如图9所示。

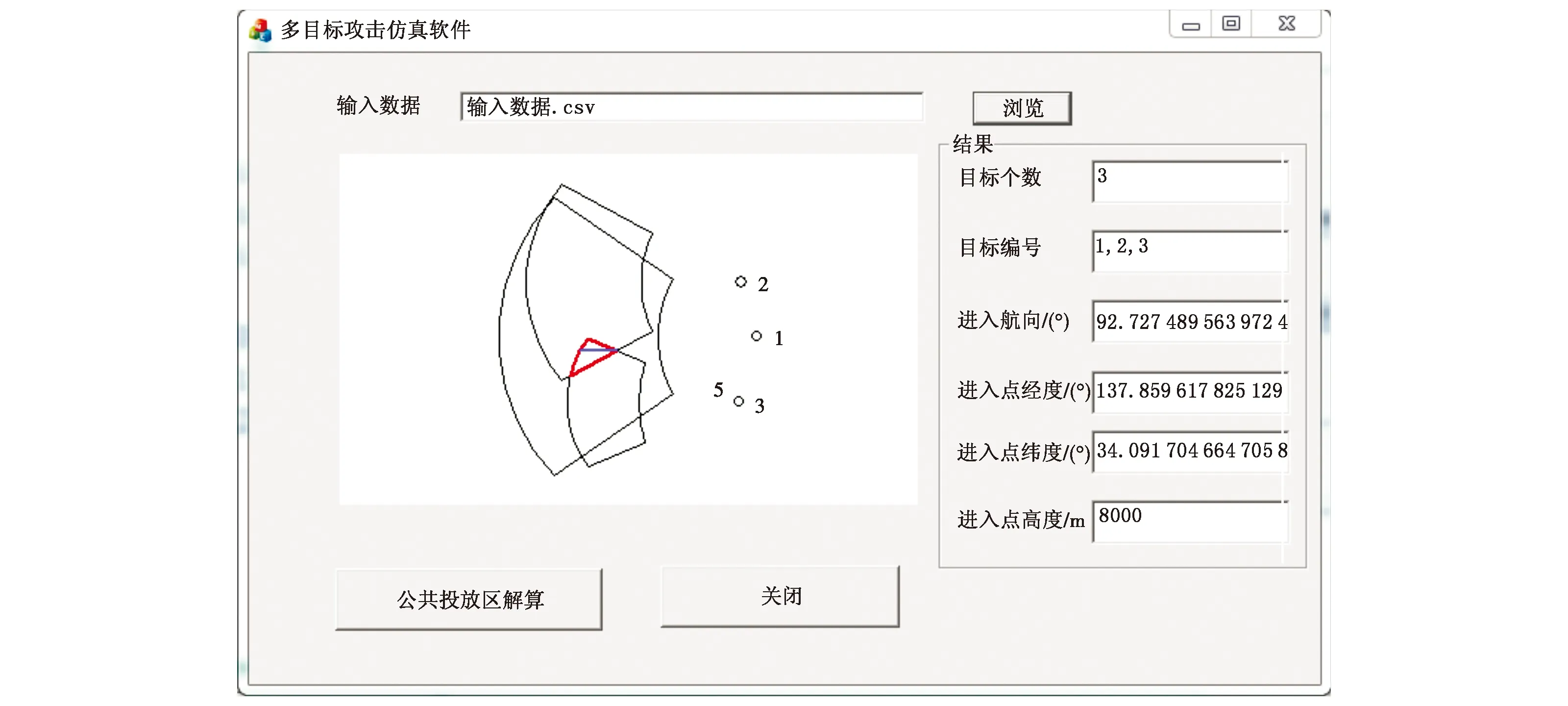
图9 多目标攻击仿真2结果Fig.9 Multi-target attacking result of Simulation 2

5 结论

多目标攻击的仿真试验结果说明公共投放区算法模型正确可行，系统能够正确进行多目标攻击解算，解算结果正确，达到了预期的试验目的。在待攻击目标中，依次进行多目标攻击解算，可将所有目标划分为可同时攻击的多个多目标批次，根据各批次对应的进入点，进而得到多目标攻击区航路，解算结果可以引导飞行员攻击占位及多目标攻击。