基于改进NURBS曲线插补算法的食品分拣机器人轨迹规划
姚学峰 李 超
(1. 沈阳职业技术学院,辽宁 沈阳 110045;2. 辽宁科技大学,辽宁 鞍山 114051)
随着工业4.0时代的来临,各国都着眼于制造业的转型升级,提高制造和自动化水平[1]。在包装、医药、食品等领域,大量的抓取和搬运需要反复进行。Delta机器人以其高刚度、高运动速度、高承载比等优点在食品、医疗等轻工业中得到广泛应用[2]。为了实现Delta机器人的稳定高速运行,充分发挥其高速运行的性能特点,有必要在工作环境中进行轨迹规划,以实现机器人的轨迹最优。
目前,国内外研究人员对并联机器人的轨迹规划方法做了大量的研究,并取得了一些优秀的成果。常用的轨迹规划方法有多项式插值、B样条曲线和Bezier曲线等[3]。韩基伟等[4]提出了一种基于过渡圆弧的Delta机器人运动轨迹规划方法。结果表明,该机器人运动稳定,无抖动缺陷,具有良好的动态特性。张浩宇等[5]提出了一种神经网络与NURBS算法相结合的轨迹规划方法。结果表明,该策略的迭代次数和执行时间相对较低,位置偏差控制在0.01 mm以内,方向偏差控制在0.01°以内。刘现伟等[6]提出了一种基于叠加摆线运动规律的Delta机器人运动轨迹规划方法。结果表明,该轨迹规划方法相比于传统方法运动更加平稳、运行效率更高。刘现伟等[7]提出了一种基于合成运动的Delta机器人运动轨迹规划方法。结果表明,基于合成运动的圆弧轨迹运动特性曲线比传统方法轨迹运动特性曲线更平滑、更自然,角加速度峰值和终端加速度峰值分别降低了60%和80%。但上述研究也存在一些问题,如曲线连接不光滑、计算复杂等,需要进一步提高适应性。
研究针对Delta并联机器人的最优运动时间,拟提出一种基于NURBS插值算法和改进遗传算法的食品分拣机器人轨迹规划方法,并采用改进的遗传算法对NURBS样条曲线进行优化,通过仿真验证该方法的可行性,以期为食品分拣机器人的研制提供一定的参考。
1 系统概述
图1所示高速并行食品分拣机器人的系统结构。系统主要由两部分组成:上位机系统和下位机系统。其中,下位机控制系统是Delta机器人的核心指令部分[8]。其主要功能是驱动机器人本体以稳定、协调、快速的方式完成既定的运动规划和抓取任务,满足工作要求。上位机系统的主要功能是可视化、模型分析、数据集成处理以及与下位机的信息交互。
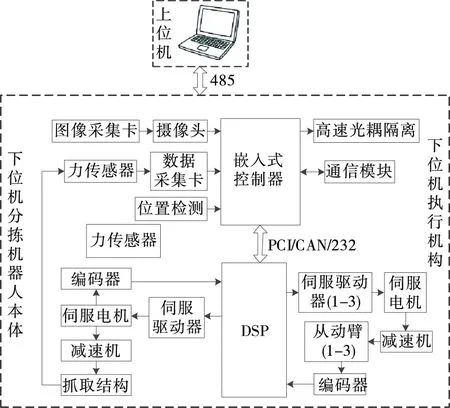
图1 系统结构Figure 1 System structure
食品分拣机器人的本体结构主要由三部分组成(见图2):静平台、动平台和3个运动支链[9]。动、静平台通过运动支链链接,静平台由电机座和固定座组成。动平台安装执行器,主要完成物体抓取等操作。3个运动支链完成关节运动到空间位置的转换。
图3为机器人的简化模型。对运动支链进行简化,简化为LA和LB。在动平台和静平台上,3条支链的连接点以120°均匀分布,分别对动平台和静平台进行简化,得到两个外圆半径为R,r的等边三角形机构。

图3 机器人简化模型Figure 3 Food sorting robot model

2 轨迹规划
为了规划一条平滑的轨迹,并使任务时间最小化,提出了一种通过改进遗传算法来优化NURBS曲线。
2.1 优化模型
2.1.1 目标函数 能耗和时间在Delta机器人轨迹优化中应用最为广泛,文中采用最小时间法,其优化函数如式(1)所示[10]。
(1)
式中:
T——规划时间,ms;
hi——第i段曲线时间,ms;
n——型值点数。
2.1.2 约束条件 文中考虑插值点处的速度约束,如式(2)所示[11]。
(2)
式中:
Vmax——运行最大速度,mm/s;
ρi——曲率半径,mm;
hmax——弓高误差,μm;
An,max——法向加速度对速度的最大限值,mm/s2;
Ts——插补周期,ms。
2.2 NURBS曲线插补算法
NURBS作为通用数学描述方法,用于生成和表示曲线、曲面。NURBS曲线的一般形式定义如式(3)所示[12]。
(3)
式中:
u——曲线的控制变量,u∈[0,1];
n——插值点数;
k——插值基函数次幂;
ωi——权值因子,ω1>0,ωn>0,其余均≥0;
Ni,k(u)——基函数。
节点向量选择如式(4)所示[13]。
U=[u0,u1,…,uk,uk+1,…,un,un+1,…,un+k+1]。
(4)
其中仅规定开始节点向量和终止节点向量的选择。通常选取u0=u=…=uk=0,un+1=…=un+k+1=1,有许多方法可以选择中间n-k个向量。
Ni,k(u)基函数有许多表达式,文中采用deboor-Cox递归定义,如式(5)所示[14]。
(5)
从式(5)可以看出,插补过程用t表示u,然后对坐标点{F(t0),F(t1),…,F(tn)}进行计算。
插补是通过弦长直线来近似曲线,实际插补是求Δu的过程,可用式(3)和式(6)获得所有插补点F(ui)[15]。
ui+1=ui+Δu。
(6)
如前所述,插补可以被视为将u看作是t的映射。同时,由于采用了离散控制系统,得到了这种形式的离散形式。文中采用二阶泰勒方法。
将u关于t的函数在时刻ti处展开,如等式(7)所示[16]。
(7)
由于插值时间非常短,因此省略余项O(t-ti)3,且取t=ti+1,插补周期Ts=ti+1-ti。将式(7)变换为如式(8)所示[17]。
(8)
插补的关键是求u对于t的一阶导数和二阶导数。如式(9)所示,速度可被视为曲线长度对时间的导数[18]。
(9)
如果已知当前插值点ui,则可以获得下一个时刻插值点的坐标ui+1。其中ui=u(ti),ui+1=u(ti+1)表示离散点的坐标,计算如式(10)所示[19]。
(10)
基于二阶泰勒展开法插补算法流程图如图4所示。

图4 算法流程图Figure 4 Algorithm flow chart
2.3 优化的NURBS曲线
为了规划一条平滑的轨迹并尽可能缩短完成任务所需的时间,提出了一种通过改进遗传算法来优化NURBS曲线。文中采用一种改进的遗传算法来加速种群的进化,可以取得更好的效果且降低运行时间。
2.3.1 初始化种群 初始种群分布要尽可能的均匀,以覆盖所有类型的情况。这里,使用累积弦长法根据式(11)生成初始种群[20]。
(11)
式中:
Pi——型值点;
el——均匀递增的实数序列。
由式(11)可以得到种群的初始值,分布也较为均匀。
2.3.2 优化交叉和变异概率 为了实现保留最优个体的目标,需要遵守两个约束:① 尽可能多地保留最优个体的基因来产生下一代,确保优秀基因的遗传[21];② 优秀个体的变异概率要尽可能低,以避免破坏优良基因[22]。为了满足上述两个条件,对交叉和变异概率进行优化,如式(12)和式(13)所示。
(12)
(13)
式中:
pc1、pc2——交叉概率;
pm1、pm2——变异概率;
fmax、fmin——种群个体的最大和最小适应度;
favg——种群个体的平均适应度;
f——变异个体的适应度;
f′、f″——选择个体中最大和最小适应度。
实现步骤:
步骤1:对优化的问题进行描述,确定目的和适应度函数。
步骤2:问题编码。选择适当的编码方法进行编码。
步骤3:初始化。通过优化方式产生生成一个约定大小的种群。
步骤4:计算适应度。计算群体中各染色体的适应度。
步骤5:通过遗传操作(选择、交叉、变异),生成新的个体。
步骤6:更新种群。将新产生的个体添加到种群中,并删除原个体以获得新的种群。
步骤7:确定终止条件。新生成的种群用于确定是否满足预置的终止条件,满足则优化结束。否则,重复上述过程。优化算法流程图如图5所示。

图5 优化算法流程图Figure 5 Flow chart of optimization algorithm
3 仿真结果与分析
3.1 仿真参数
为了评估所提规划方法的性能,验证所提方法的有效性,仿真设备为联想PC,操作系统为Windows 10 64位旗舰,CPU为Intel I5 2450m,频率为2.5 GHz,内存为8 GB。利用仿真工具MATLAB完成仿真。如表1所示NUBRS曲线参数(型值点和权值)。每个点的权重初始化为1。

表1 NUBRS曲线参数Table 1 NUBRS curve parameters
仿真过程中必须遵循一定的参数约束,具体参数约束情况如表2所示。

表2 约束情况Table 2 Constraints
3.2 仿真分析
采用改进遗传算法来优化NURBS曲线,对并联机器人进行轨迹规划仿真,并与改进后的NURBS曲线进行比较。通过插补点和权值产生NURBS曲线,采用二阶泰勒方法生成离散点信息,采用改进遗传算法优化NURBS曲线。不同规划算法的比较如图6所示。根据上述数据,得到一条NURBS曲线,即图中的虚线。改进遗传算法优化的曲线为图中的实线。

图6 分拣机器人笛卡尔空间轨迹Figure 6 Cartesian space trajectory of sorting robot
从图6可以看出,优化前后的曲线都经过了类型值,有效满足了笛卡尔空间的插补要求。优化后的规划轨迹更平滑、更短。通过运动学反解,将笛卡尔空间坐标信息转化为关节空间坐标信息。优化前关节空间曲线轨迹如图7所示。表3为通过型值点的时间(优化前)。图8为优化后关节空间曲线轨迹。表4为通过型值点的时间(优化后)。
由图7和图8可以看出,改进遗传算法优化后的关节空间机器人曲线比优化前的NURBS曲线更加平滑。由表3和表4可以看出,优化后机器人通过型值点的时间由3 230 ms降低到3 070 ms,相比于优化前降低了160 ms,时间优化率提高了5.0%左右。说明该轨迹规划方法可以有效地提高食品分拣机器人的稳定性和效率。
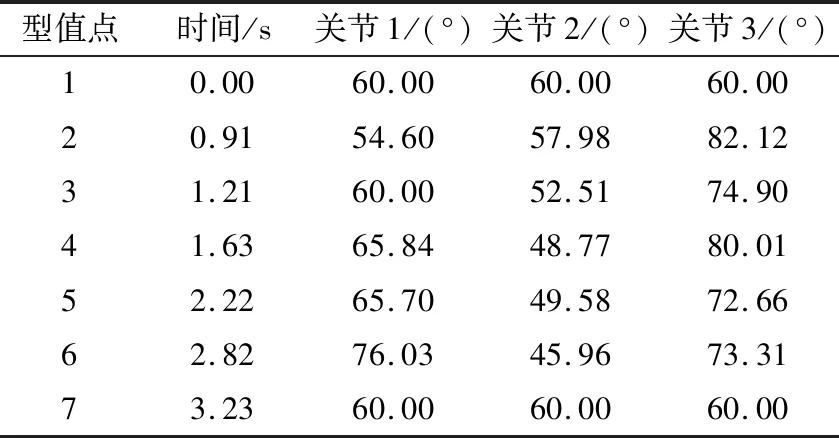
表3 优化前关节型值点时间Table 3 Joint type value point time before optimization
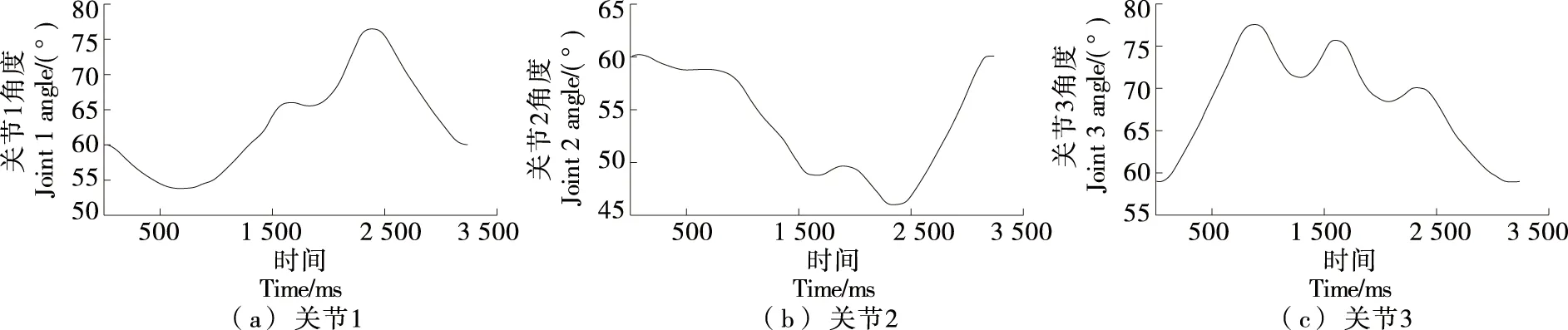
图7 优化前分拣机器人关节空间角度变化Figure 7 Changes of joint space angle of sorting robot before optimization

图8 优化后分拣机器人关节空间角度变化Figure 8 The joint space angle changes of the sorting robot after optimization

表4 优化后关节型值点时间Table 4 Optimized joint type value point time
4 结论
文中以运行时间最优为目标,提出了一种结合NURBS插值算法和改进遗传算法的食品分拣机器人轨迹规划方法。采用改进的遗传算法优化NURBS曲线。结果表明,文中所提优化方法在关节空间的机器人曲线比优化前更加平滑,运行时间从优化前的3 230 ms降低到优化后的3 070 ms,在一定程度上提高了食品分拣机器人的稳定性和效率。文中食品分拣机器人的轨迹规划方法尚处于起步阶段,仅对轨迹规划方法进行仿真分析,后续将进行试验分析,不断提高轨迹规划方法的性能,完善食品分拣机器人系统。

