基于三方程VLES模型的进水池吸气涡数值模拟

黄先北 郭 嫱 仇宝云

(扬州大学电气与能源动力工程学院， 扬州 225127)

0 引言

开敞式进水池(后文简称进水池)是轴流泵站常用的进水形式，主要特征在于水面上方与空气直接接触，形成典型的自由界面。受进水池结构以及水位变动的影响，喇叭管淹没深度往往不足而导致池内存在明显的漩涡，引起振动、噪声以及泵效率下降[1-4]。若漩涡将水面上方空气吸入，轴流泵站进水池则形成吸气涡，进一步加剧了泵的振动与噪声，同时易导致空化与气蚀[5-6]。因此，研究进水池吸气涡意义重大。

分析吸气涡特征及机理，关键在于准确获取吸气涡流场结构。随着计算流体动力学(Computational fluid dynamics，CFD)技术的快速发展，近年来已有不少研究采用该技术[7-13]对吸气涡进行数值模拟。影响模拟精度的因素主要有湍流模型、网格数和模拟时间[7-16]。

除上述因素之外，还应考虑吸气涡现象中水与空气的交界面捕捉方法。根据现有研究，耦合水平集与流体体积(Coupled level-set and volume-of-fluid， CLSVOF)方法较优[10,14,17-18]。

本文以文献[19]的进水池为研究对象，基于非常大涡模拟(Very large eddy simulation，VLES)模型，从网格数量级以及模拟的物理时间两方面进行分析，为进水池吸气涡的准确模拟提供参考。

1 数学模型

1.1 非常大涡模拟

基于涡粘假设，不可压流动的雷诺平均Navier-Stokes方程形式为

(1)

式中u——速度矢量，m/st——时间，s

ρ——密度，kg/m3p——压力，Pa

ν——流体的动力粘度，Pa·s

νt——涡粘系数，Pa·s

S——应变率张量，s-1

St——动量源项，m/s2

考虑到吸气涡有局部旋转效应，应在模型中加以体现。为计算νt，文献[20]提出的三方程k-ω-v2模型为

(2)

(3)

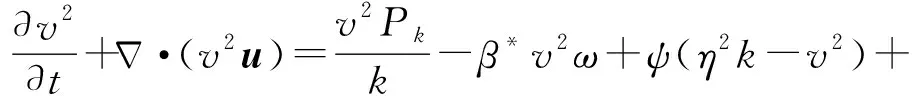
(4)

其中

α=0.44-0.116F1
σω=0.856-0.356F1
βω=0.082 8-0.007 8F1
ψ=0.162ω
σk=1-0.15F1

式中k——湍动能，m2/s2

Pk——湍动能生成率，m2/s3

F1——耦合函数

ω——湍动能比耗散率，s-1

β*——模型系数，取0.09

CDkω——交叉耗散项，s-2

v2——垂直于壁面方向的雷诺正应力，m2/s2

ψ——修正的比耗散率

η——涡粘系数修正率

涡粘系数定义为

(5)

式中a1——模型系数，取0.31

S——应变率张量的模，s-1

F2——模型转换函数

为了实现混合RANS/LES，基于文献[15]的方法，将涡粘系数修正为

(6)

其中

(7)

式中γ——模型系数，取0.002

n——模型系数，取2

Lc——截断尺度，m

Li——湍流积分尺度，m

Lk——Kolmogorov尺度，m

Δx——网格在x方向的尺度，m

Δy——网格在y方向的尺度，m

Δz——网格在z方向的尺度，m

1.2 S-CLSVOF

本文采用文献[21-22]简化后的版本，命名为Simple coupled level-set and volume-of-fluid(简称S-CLSVOF)。为便于编译该方法，本文选用开源CFD软件OpenFOAM-2.2.x，其中液相体积分数的输运方程为

(8)

式中αl——液相体积分数，%

uc——压缩速度，m/s

采用均相流模型处理液相、气相，即两相的速度与压力相等。

为了将体积分数与动量方程相耦合，将表面张力作为式(1)的动量源项，定义为

(9)

其中

(10)

(11)

γ=1.5xΔ

(12)

式中σ——表面张力系数，N/m

φ——流场中某点至交界面的无量纲距离

xΔ——距离交界面最近的网格尺度，m

2 进水池算例描述

2.1 几何与网格

进水池的几何如图1所示。为便于模拟，将进水池分为进水管域、空气域以及水域，各域之间采用交界面连接。除图1所示的几何参数外，喇叭口直径为0.15 m，同时，进水管中心偏离进水池中心线，距离两侧壁面分别为0.14 m与0.16 m，水位为0.23 m。

图1 进水池几何与计算域划分Fig.1 Geometry and calculation domain division of intake

为了分析网格数量级对计算结果的影响，本文采用网格数分别为1.61×106(M1)与1.03×107(M2)的两套网格，如图2所示，对应的平均y+分别为13～40、9～20。

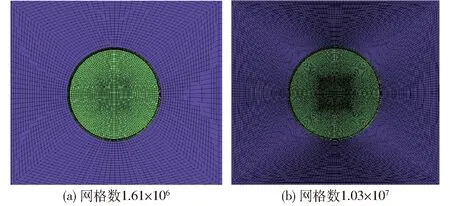
图2 进水管附近的网格分布(俯视图)Fig.2 Grid distribution near intake pipe (bottom view)

2.2 边界条件与数值算法

由于进水池被划分为3个域，不同域之间采用任意网格交界面(Arbitrary mesh interface，AMI)[23]进行处理。进口采用均匀来流速度，设定为0.241 5 m/s；出口采用流量出口，设定为0.016 7 m3/s，空气域上边界为总压边界，等于大气压；其余边界为固壁，采用壁面函数处理近壁面流动。

压力-速度求解采用PISO(Pressure-implicit with splitting of operators)算法，梯度与散度项采用二阶精度的“Gauss linear”格式进行离散，时间离散采用二阶精度的“backward”格式，时间步长为1×10-4s。

3 结果分析

3.1 网格的影响

本文以如下步骤对两套网格进行计算：基于M1计算14 s(此时吸气涡达到稳定)；以上一步的结果作为初始条件，基于M1与M2进行计算，2 000步(即0.2 s)后开始求平均，采用5.5 s内的结果作时间平均。

图3所示为喇叭口下方15 mm的线段上的速度分布，该线段与喇叭口中心线位于同一平面，如图3a所示。

由图3b、3c可见，两套网格均可捕捉到与试验[19]较为一致的速度分布规律。图3b所示的速度峰值与试验值之间存在错位，这与文献[19,24]中的CFD结果相似，推测该错位是试验中存在数值模拟中未体现的外界扰动。

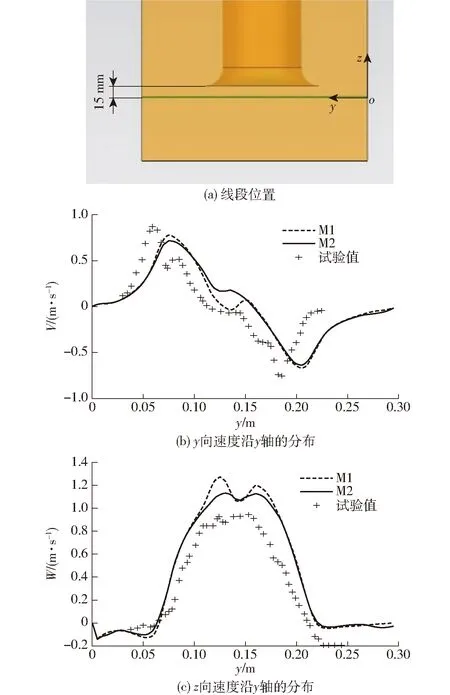
图3 喇叭口下方的速度分布Fig.3 Velocity distribution below bell mouth

图4所示为基于两网格预测的瞬时流线与水的体积分数等值面，其中流线的起点位于水面，等值面根据文献[12]的研究取αl=95%。为便于分析，图中还用箭头显示了吸气涡附近流线的总体趋势。

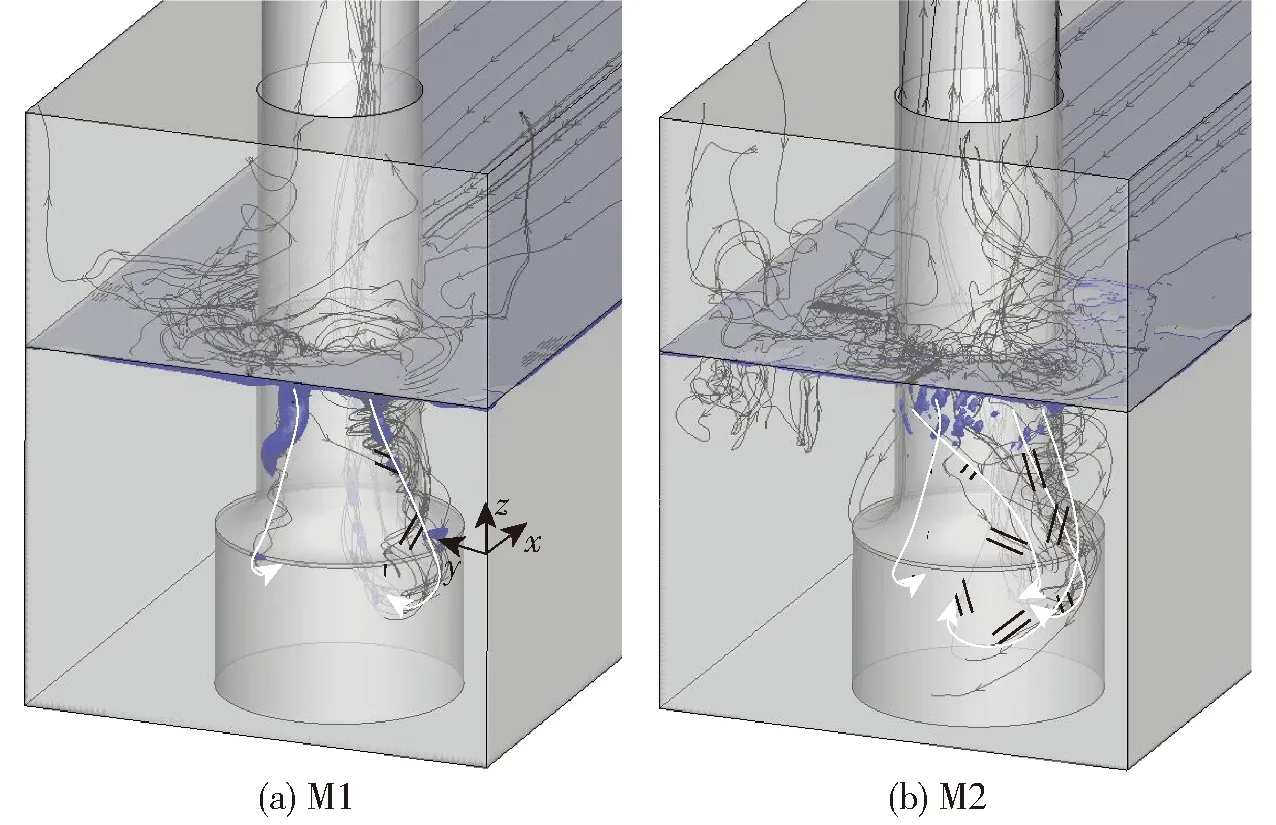
图4 瞬时吸气涡形态与流线对比(t=19.7 s)Fig.4 Comparison of instantaneous air-entrained vortex shape and streamlines

显然，尽管位置略有差异，但两套网格均预测到了水面附近的吸气涡。此外，与M1不同的是，M2所得吸气涡更加破碎，这是因为随着网格密度的增加，原本表征同一体积分数的网格被分成多个更小的网格，在迭代与插值算法的作用下，这些更小网格上的体积分数不再是同一数值，从而导致等值面变得更加零碎。为了更好地显示吸气涡，应发展一种可同时体现水面凹陷(体积分数)与漩涡的吸气涡识别准则。

为了更好地表征吸气涡的程度，采用相对吸气率，定义为

(13)

式中αl,ave——计算域出口的平均液相体积分数，%

图5所示为相对吸气率随时间的变化，为便于显示，图中曲线上两点之间的时间间隔为200时间步，即0.02 s。由图5可见，M1所得β的变化幅度高于M2，但二者的变化规律相近。计算时间平均相对吸气率，M1为2.59×10-4，M2为2.44×10-4，二者差异不大。

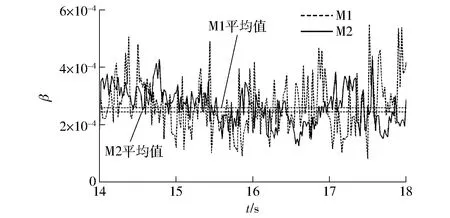
图5 不同网格计算所得相对吸气率随时间的变化曲线Fig.5 Variation of relative air-entrainment rate along with time on different meshes

综合以上分析，网格数量级达到O(106)时可以较好地捕捉到吸气涡流场的速度分布，同时也可以体现吸气涡的程度。后文将基于M1作进一步分析。

3.2 计算时间的影响

为检验计算时间的影响，基于M1网格计算至60 s。图6所示为β从t=0 s至t=60 s的变化情况。从图中可见，吸气率在0～3 s内逐渐增大，这是因为吸气涡逐步形成，具体见文献[12]。此外，由图6可知，尽管将计算延长至60 s，吸气率的变化从t=3 s开始并未出现明显的上升或下降，而是呈现出类似周期性的变化规律。

图6 M1计算所得相对吸气率随时间的变化曲线Fig.6 Variation of relative air-entrainment rate along with time on M1

为验证吸气涡在t=14 s以内是否已达到稳定，分析不同时刻下吸气涡的位置，如图7所示，吸气涡位置取自其中心坐标。从图7可见，预测得到的吸气涡存在两个集中区域，其一位于(-0.06 m,0.08 m)附近，与试验值一致，但CFD预测到了另一个位于(-0.05 m, 0.15 m)附近的吸气涡。文献[19,24]中的CFD结果同样出现了该现象，推测与上文一致，是因为试验中存在数值模拟中未体现的外界扰动。对比3～14 s以及14～60 s之间的吸气涡位置可知，计算时间的延长并未改变吸气涡的分布规律。因此，吸气涡从t=3 s开始处于稳定变化的状态，与图6吸气率的变化规律一致，而延长计算时间不会改变吸气涡的程度(相对吸气率)以及位置。

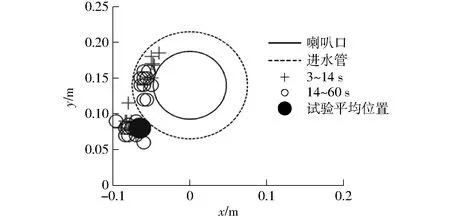
图7 自由水面上吸气涡的位置示意Fig.7 Sketch of air-entrained vortex locations on free surface

根据进水池设计标准[25]，特定形式的表面涡需至少观测10 s。因此，对于本算例而言，吸气涡稳定之后再计算10 s即可满足要求(即t=13 s)。

3.3 VLES模型特性分析

由前文结果可见，VLESk-ω-v2预测结果与试验及文献[19,24]基本一致。为分析该模型的特性，有必要分析吸气涡附近的Fr与Li，这两个变量分别代表了解析程度与湍流积分尺度。

图8所示为自由水面上Li与Fr的分布。由图8a可见，湍流尺度沿流动方向有降低的趋势，且涡心附近的值略低于周围区域。由图8b可见，进水管附近的Fr为1，说明此处为RANS模式。对于VLES或其它混合RANS/LES方法而言，降低计算量最有效的方法就是保证近壁区为RANS模式，因为RANS对近壁面网格要求较低，可以极大地降低近壁面网格密度。

对比图8a与图8b可见，二者的分布规律基本相反，即Li较高的位置则Fr较低。根据式(6)，Li越高，则Fr越低。图8所示的规律表明，在既定网格下，Fr主要受Li的影响，此时湍流积分尺度越大，则Fr越低，表明湍流的解析度越高。观察图8b可见，Fr在流动的上游较低(除壁面附近以外)，说明此时湍流基本被解析，而在进水管附近，Fr总体高于上游，这是因为存在流动分离而存在小尺度湍流结构，模型难以完全解析。

图8 自由水面上瞬时Fr、Li与流线分布(t=19.7 s)Fig.8 Instantaneous Fr and Li and streamline distributions on free surface

总体而言，本文采用的VLES模型在Li的主导下，保证了近壁区的RANS模式以及湍流核心区的混合RANS/LES模式。

4 结论

(1)VLES所得结果与试验值基本一致，且网格数量级达到O(106)时即可较好地捕捉到吸气涡的流场结构与程度。

(2)数值计算可以由相对吸气率随时间的变化规律判断吸气涡是否达到稳定，根据标准要求，在此之后计算10 s即可，进一步延长计算时间并不影响吸气涡的程度与位置。

(3)既定网格下，VLES模型的解析度主要受湍流积分尺度的影响，近壁面为RANS模式，保证了相对较低的计算量，而在湍流核心区为混合RANS/LES。