具有混合执行器故障的多智能体分布式有限时间自适应协同容错控制
张 普, 薛惠锋, 高 山, 左 轩
(西北工业大学自动化学院, 陕西 西安 710129)
0 引 言
近年来,多智能体系统协同控制技术在人工智能发展中具有重要作用,吸引了大量学术界和工业界学者的研究目光。其在军事和民用方面均有广泛的应用,例如无人机集群、机器人协作,森林火灾救援等方面。这些应用对多智能体系统协同控制技术的可靠性和控制精度均有较高的要求,然而,随着智能体系统的复杂程度逐渐增大,系统发生故障的可能性也越来越频繁。尤其是执行器故障问题,如果不能及时地进行有效的容错处理,不仅智能体系统的协同性能受到影响,甚至会导致整个目标任务的失败。基于此,本文着眼于研究多智能体系统中执行器发生故障时的协同容错控制技术。
目前,学者们基于先进控制理论已经提出了很多关于具有执行器故障的多智能体系统的容错控制方法。文献[4]采用一种分层容错控制策略,底层为故障检测、隔离及重构,上层为预测与补偿故障,为一类四旋翼无人机编队解决了执行器卡死故障。文献[5]针对严参数反馈非线性系统,提出了一种完全分布式自适应容错控制器,解决了部分失效型执行器故障问题。文献[6]设计了一种鲁棒自适应容错控制律,补偿执行器偏置故障和部分失效执行器故障。文献[7]提出了一种事件触发容错控制方法,用于解决执行器故障问题。文献[8]基于自适应滑模观测器,构建了一种分布式协同容错控制器,补偿执行器失效故障和偏置故障。文献[9]提出了一种基于在线重构的自适应协同容错控制策略,用于补偿异构多智能体系统的时变失效故障和加性执行器故障。文献[10]采用delta算子的方法设计了一种H/H模型预测容错控制方案,解决时变执行器故障问题。文献[11]设计了一种基于虚拟执行器的协同容错策略,通过对称控制器和观测器相结合,来隐藏执行器故障对系统的影响。在上述研究中,大多是基于执行器故障模型中具有一种或两种类型故障展开的研究。然而,在实际工程中,非线性多智能体的执行器故障类型不仅未知,而且不止一种或两种,并可能伴随有混合故障类型的现象。此外,除了未知故障问题,系统模型中的控制增益参数一般也不具有先验性。因此,有必要针对同时具有未知混合执行器故障及未知动态控制增益的非线性多智能体系统的容错控制问题展开深入研究。
值得关注的是,上述研究主要针对未知故障和未知控制增益参数所引起的多智能体系统不稳态性能,没有涉及到瞬态性能问题,即有限时间内稳定问题。而在诸多有关多智能体系统的实际工程应用中,诸如无人机、航天器以及机器人的姿态等,不仅需要有效克服执行器故障所引起的系统不稳定,并且需要系统在有限时间收敛到零或者零点的邻域内,最终使多智能体系统实现渐近稳定。因此,尽管上述文献提出了很多解决多智能体系统执行器故障的容错控制方法,然而很少能够在有限时间内有效地解决具有混合执行器故障和未知控制增益的多智能体系统协同容错问题,并且保持沿预设编队轨迹运动。
因此,本文针对一类高阶严反馈非线性多智能体系统,基于动态面控制和自适应反推技术相结合,提出了一种自适应协同容错控制策略,解决系统模型中含混合执行器故障和不确定非线性参数问题。主要贡献有以下几点:
(1) 考虑了混合执行器故障,针对一类更具一般性的具有未知混合执行器故障的干扰高阶非线性多智能体系统,提出了一种新颖的基于动态面控制的自适应容错控制策略。在文献[4-11]中,作者仅能解决一种或两种执行器故障。与上述文献相比,本文所提方法同时考虑了不同类型的执行器故障,在拓宽应用潜力方面具有重要意义。
(2) 与现有文献的神经网络估计技术相比,本文所提的径向基函数神经网络(radial basis function neural networks, RBFNNs)自适应技术,不仅能够在线精确估计不同类型故障,实时补偿未知的混合执行器故障,并对系统模型中的未知动态参数实现局部最优估计。因此,所提方法在混合故障情形下依旧能够保持良好的容错能力。
(3) 与现有方法相比,所设计的分布式有限时间控制器,基于有限时间理论与一致性协议,能够确保多智能体系统在有限时间达到稳定状态,并以预设队形运动。
1 预备知识
1.1 图论及通讯条件
一个有向网络可以用=(,,)表示,是用于建立智能体之间通讯模式的数学工具。其中={,,…,}是个节点的集合,⊆×是有向边的集合,=()×∈×是加权邻接矩阵,满足>0。而且,中有向边表示一个有序点对(,),即从到的有向信息流,也就是说节点可以获得节点的信息。当且仅当中存在有向边(,),邻接矩阵中的每个元素>0,否则=0(≠;,=1,2,…,)。此外,本文均不考虑自环,即=0(=1,2,…,)。若邻接矩阵满足=,则称该特殊情况下的=(,,)为无向网络。
信息交互是多智能体系统实现协同控制的必要条件。
1.2 RBFNNs理论
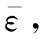
()=()+()
(1)
式中:∈⊂表示RBFNNs的输入向量;=[,,…,]表示权重向量;表示隐藏层;()是径向基函数向量。
本文所选的径向基函数为高斯函数,其表达式为
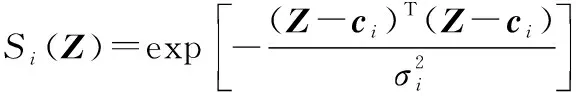
(2)
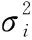
理想的权重是由最小估计误差优化而来。
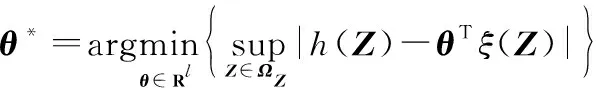
(3)
式中:表示实数。基于理想权重,()是给定的光滑函数,对式(1)进一步求解,可得未知的非线性函数如下:
()=()+()
(4)
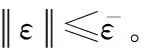
1.3 有限时间理论
原点是有限时间稳定平衡的,当且仅当原点是Lyapunov稳定且存在原点的开邻域⊆和一个被称为设定时间的正定义函数():→使得对于所有(0)∈{0},有
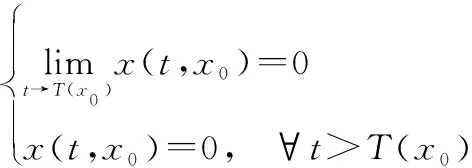
(5)
此外,如果原点在=上是有限时间稳定的,则原点是全局有限时间稳定平衡的。而且,原点的有限时间稳定性也意味着原点的渐近稳定性。

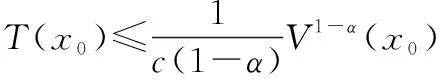
(6)
对于非线性系统,假设存在一个连续光滑正定函数()和标量>0, 0<<1,>0使得
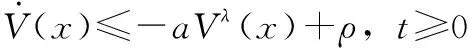
(7)

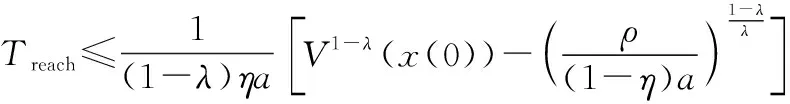
(8)
对于,∈,0<<1,有如下不等式成立:
(+)≤+
(9)
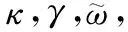
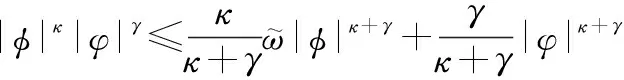
(10)
2 系统模型
2.1 执行器故障模型
智能体的执行器故障主要是由于智能体出现老化、损伤,通讯失效以及传感器失效等形成部分失效故障、完全失效故障、偏置故障、卡死故障等4种故障,其数学模型如下:
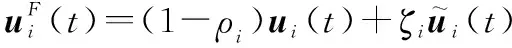
(11)
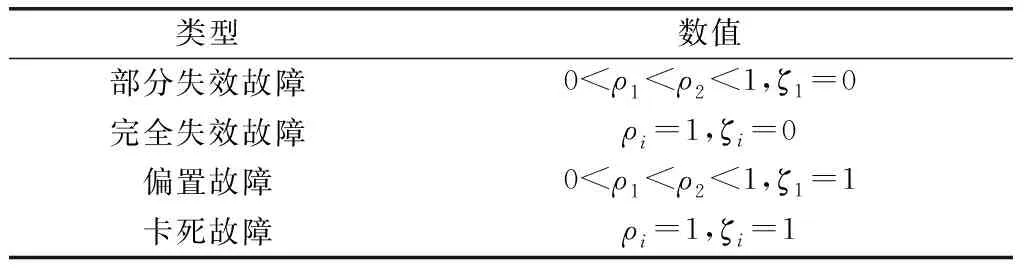
表1 执行器故障类型Table 1 Actuator failure types
综合分析,可得系统执行器故障模型如下:
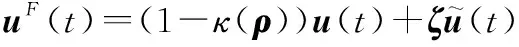
(12)

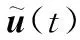
多智能体编队系统在实现预期控制目标过程中,当某一个智能体的执行器出现部分失效故障时,多智能体系统由于通信的中断,有可能引起执行器不能正常运行,表现为部分失效现象。
多智能体编队系统预设的队形编队运动,每个智能体的轨迹均为一条光滑的函数,存在一个正常数,使得满足以下紧集:
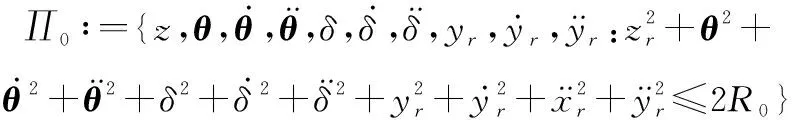
(13)
2.2 多智能体模型
考虑一类包含个智能体的多智能体系统,每个智能体具有不确定性的严反馈非线性动态性能,模型表示为
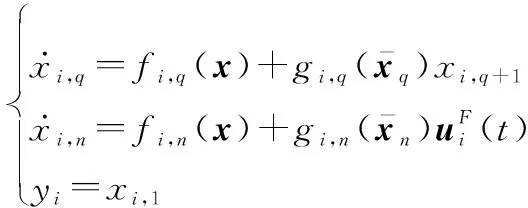
(14)
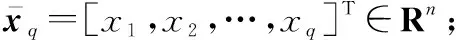
时变参考轨迹是连续有界的,则控制系统式(14)是一个闭环稳定系统且能够追踪给定的参考轨迹信号。
3 跟踪控制律设计
基于执行器故障模型式(12)和系统模型式(14)进行容错控制律设计,其过程如下。
定义跟踪误差:
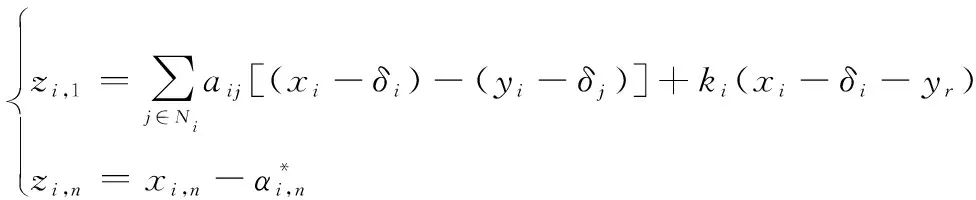
(15)
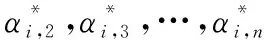
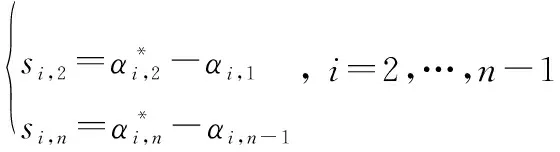
(16)
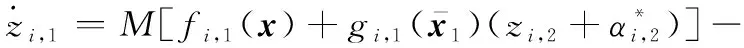
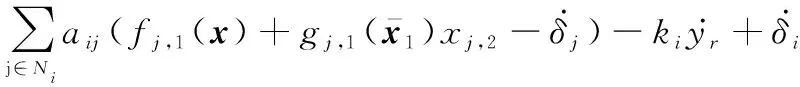
(17)
式中:=∑∈+。
根据RBFNNs,式(17)可进一步改写为
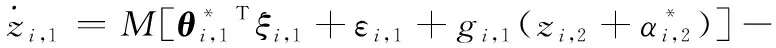
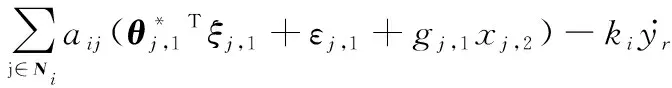
(18)
构建Lyapunov函数如下:
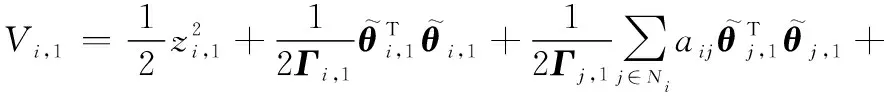
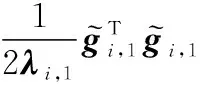
(19)
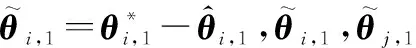
对式(19)时间求导,得
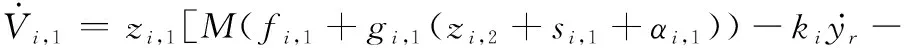
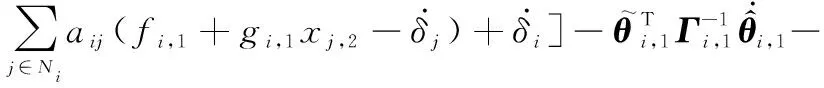
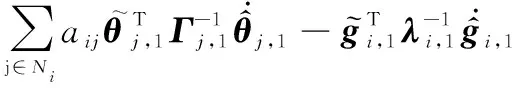
(20)
应用第12节的RBFNNs,对未知函数,1和,1逼近处理,得
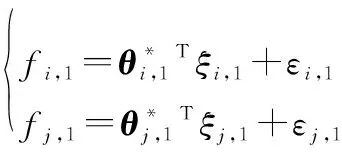
(21)
根据引理5和Young’s不等式,可知
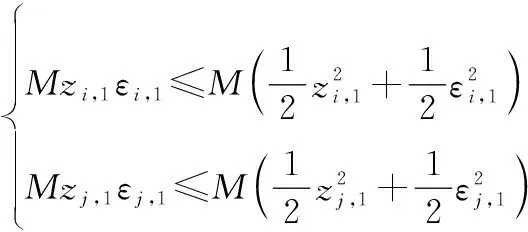
(22)
将式(21)和式(22)代入式(20),可得
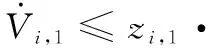
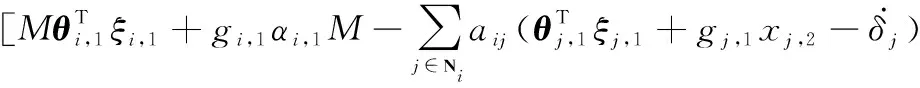
4)训练方式、手段及步骤:将学生分成几个小组(5人一组),每个小组确定说话的类型,小组内进行谈论,要求每位学生都参与,说话时间至少3分钟;小组训练结束后,教师在随机抽取各小组几名学生,进行即兴说话,学生和老师按照既定标准进行的评分和点评。
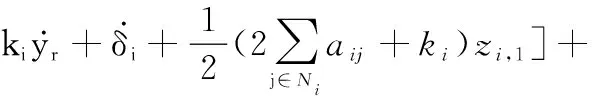
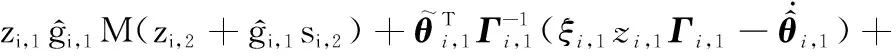
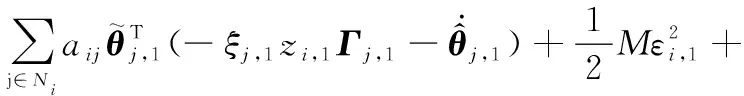
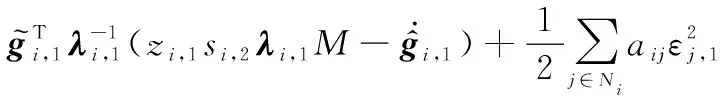
(23)
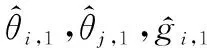
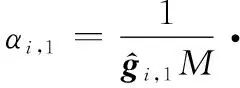
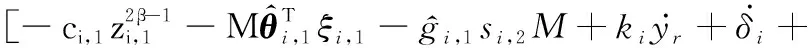
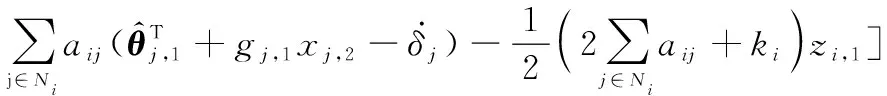
(24)
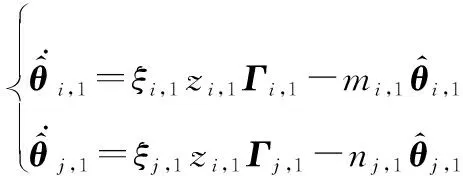
(25)
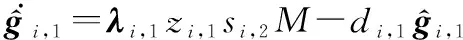
(26)
式中:,1、,1、,1、,,为设计常数。
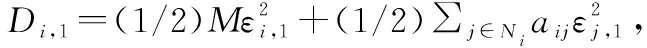
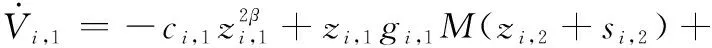
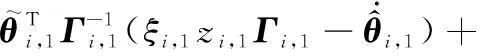
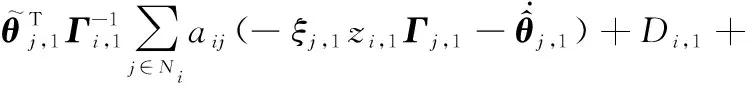

(27)
将式(25)和式(26)代入式(27),则有
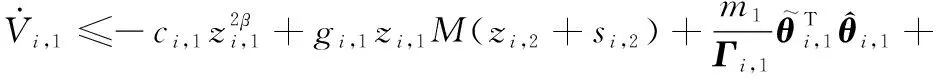
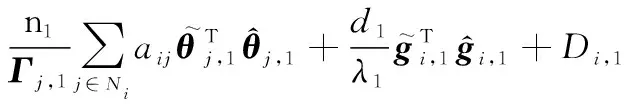
(28)
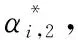
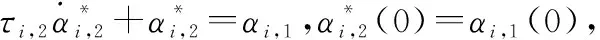
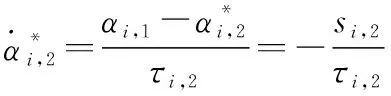
(29)
由此可知
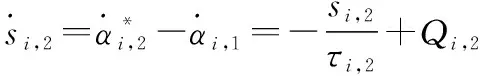
(30)
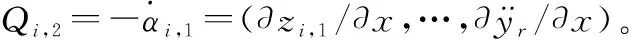
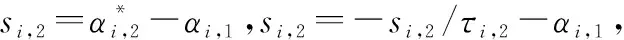
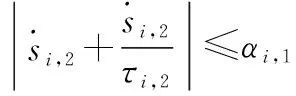
(31)
根据引理4和引理5,则有
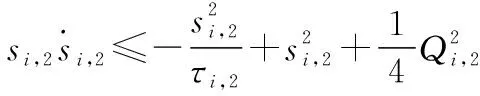
(32)
定义新误差如下:
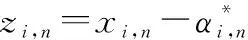
(33)
对式(33)求导,可得
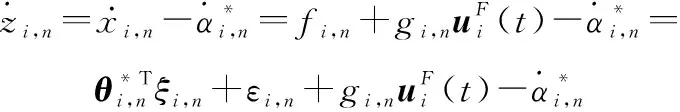
(34)
同理,选取构建Lyapunov函数如下:

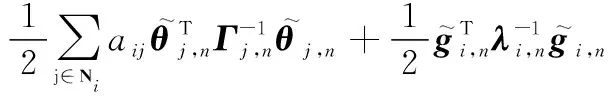
(35)
对式(35)时间求导,可得
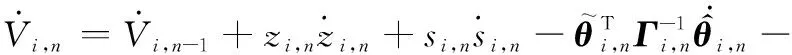
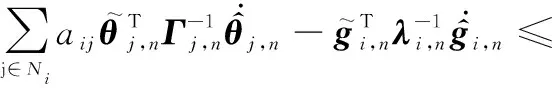
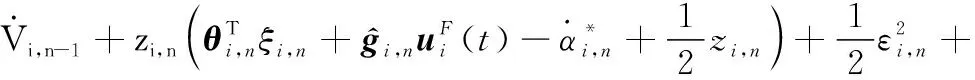
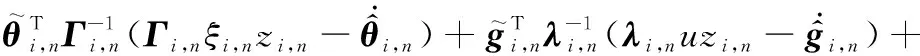
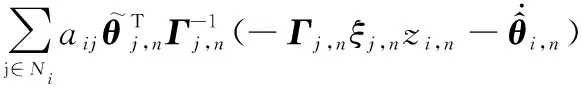
(36)
根据式(12),式(36)进一步化简为


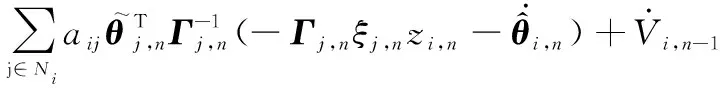
(37)
根据RBFNNs逼近理论,可得
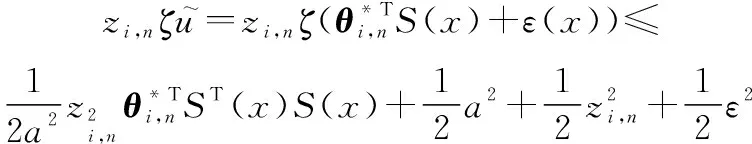
(38)
联立式(37)和式(38),可得
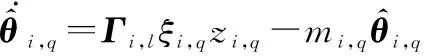
(39)

(40)
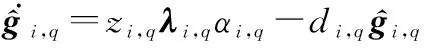
(41)
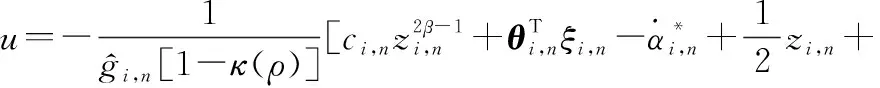
(42)
将式(39)~式(42)代入式(37),可得
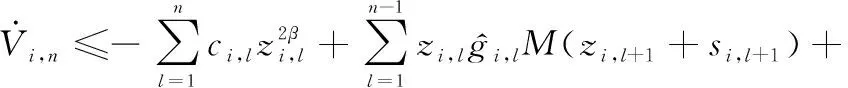
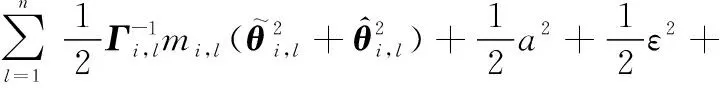
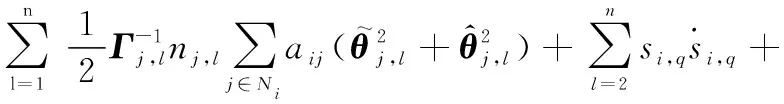
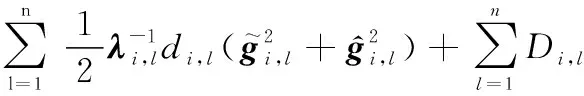
(43)
根据引理4和引理5,可得
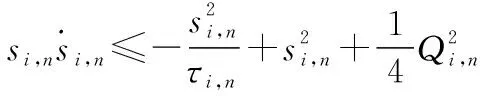
(44)
将式(44)代入式(43),则有
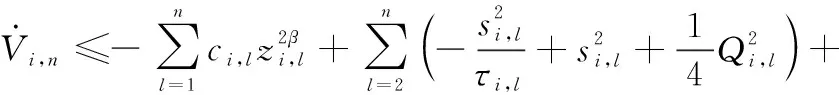
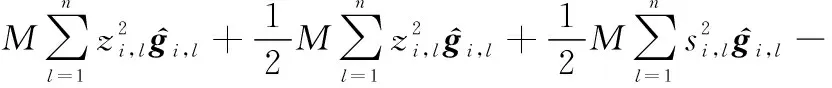
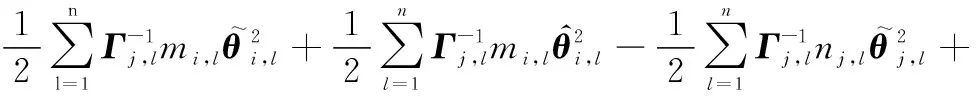


(45)
根据引理5,对式(45)进行变换,则有
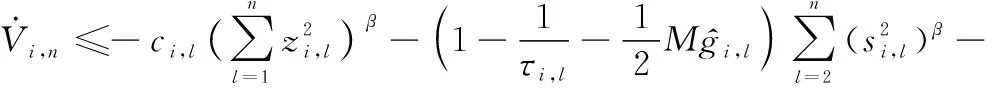
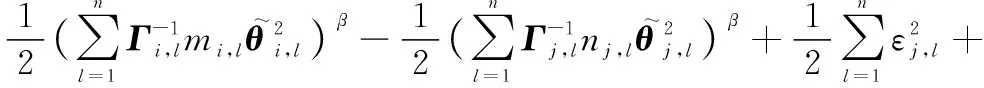
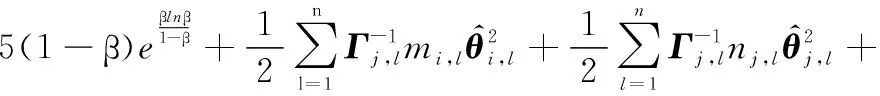
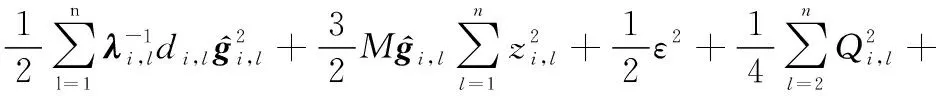
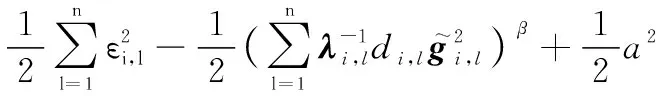
(46)

根据有限时间定理,式(46)可进一步简化为
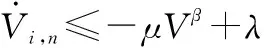
(47)
式中:
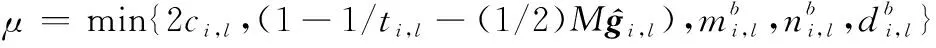
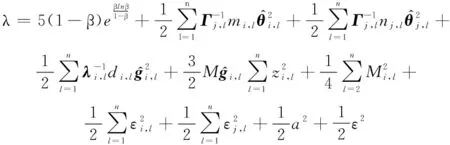
于是,可进一步得出给定时间如下:
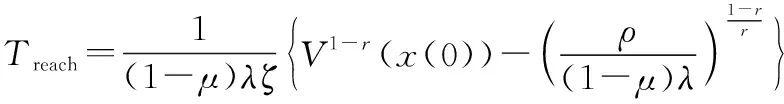
(48)
4 稳定性分析
高阶非线性多智能体系统式(13)在满足假设1至假设3的前提下,利用分布式动态面控制和分布式自适应控制,能保证控制系统目标的实现,即高阶非线性多智能体系统式(14)的状态能最终以预设队形实现渐近一致追踪的目的。
为了分析所设计控制律的稳定性,构建整个闭环系统的Lyapunov函数如下:
=1+2
(49)

对式(49)求导,可得
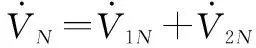
(50)
于是,可得

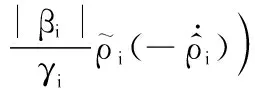
(51)
根据引理5、追踪误差式(15)、边界误差式(16)、RBFNNs式(1)以及有限时间理论式(5),式(51)可进一步重写为
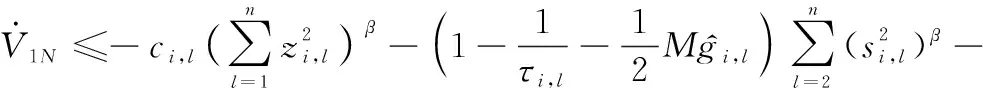
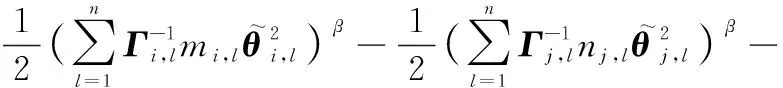
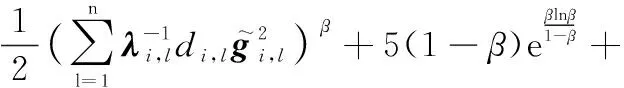
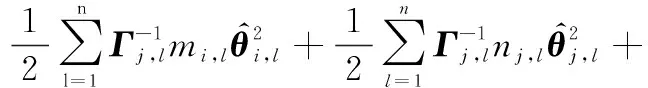
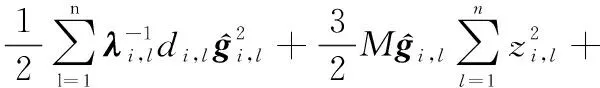
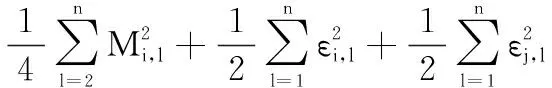
(52)
同理,2的导数如下:
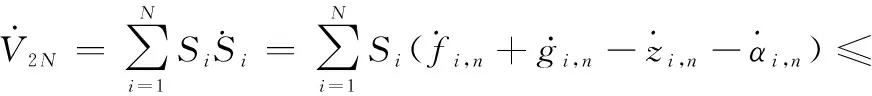

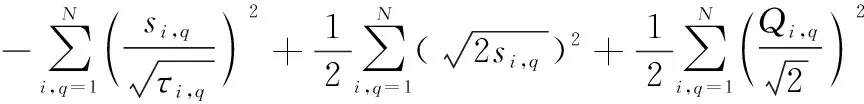
(53)
式中:
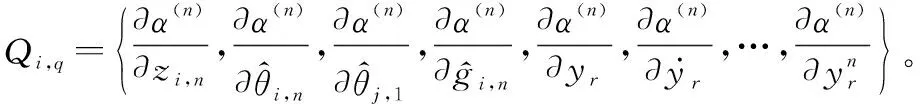
于是,联立式(52)和式(53),可得
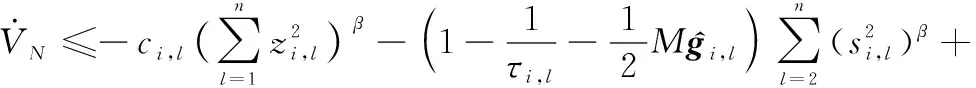
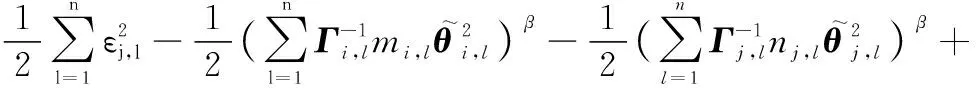
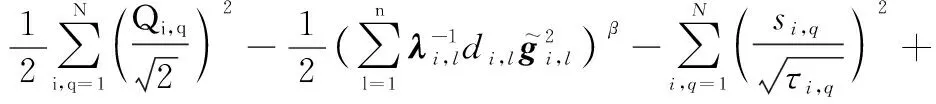
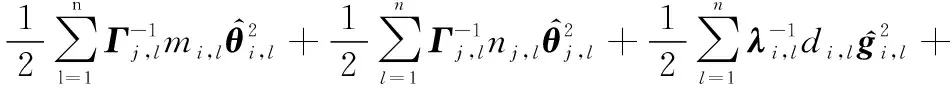
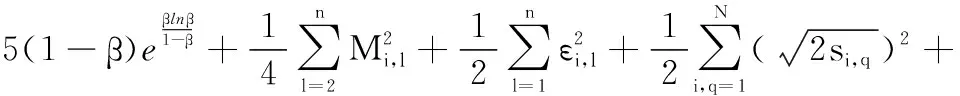
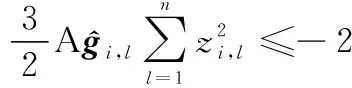
(54)
式中:
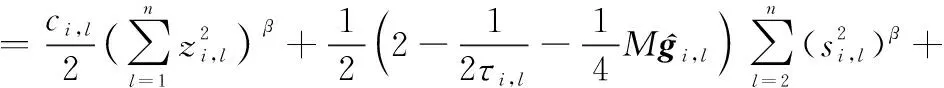
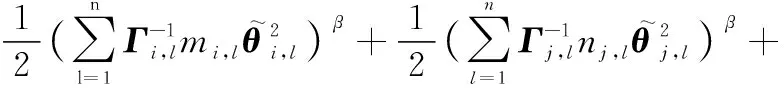
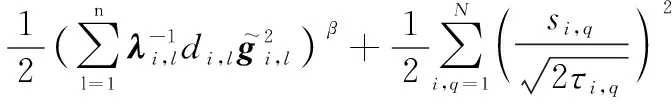
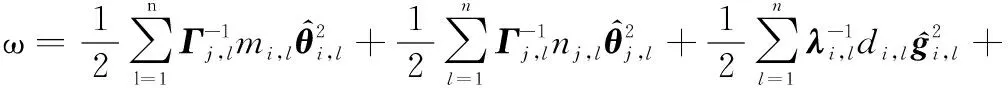
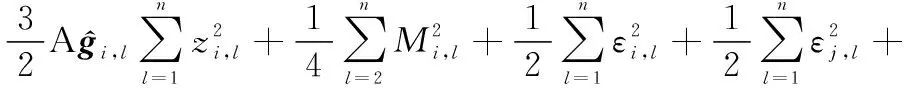
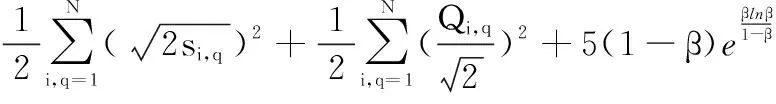
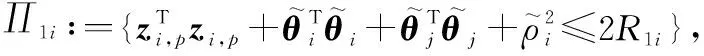
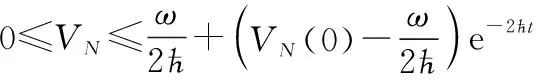
(55)
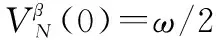
因此,当时间足够大时,多智能体系统的跟踪误差,,…,在有限时间收敛,而且均为有界的,从而实现多智能体系统在执行器故障的情形下有限时间集结预设队形,并保持该队形追踪运动目标。
证毕
5 仿真实验
在本节中,采用由(=10)个智能体组成的多智能体系统有向拓扑结构,其中包括一个领航者和-1个跟随者(见图1)。
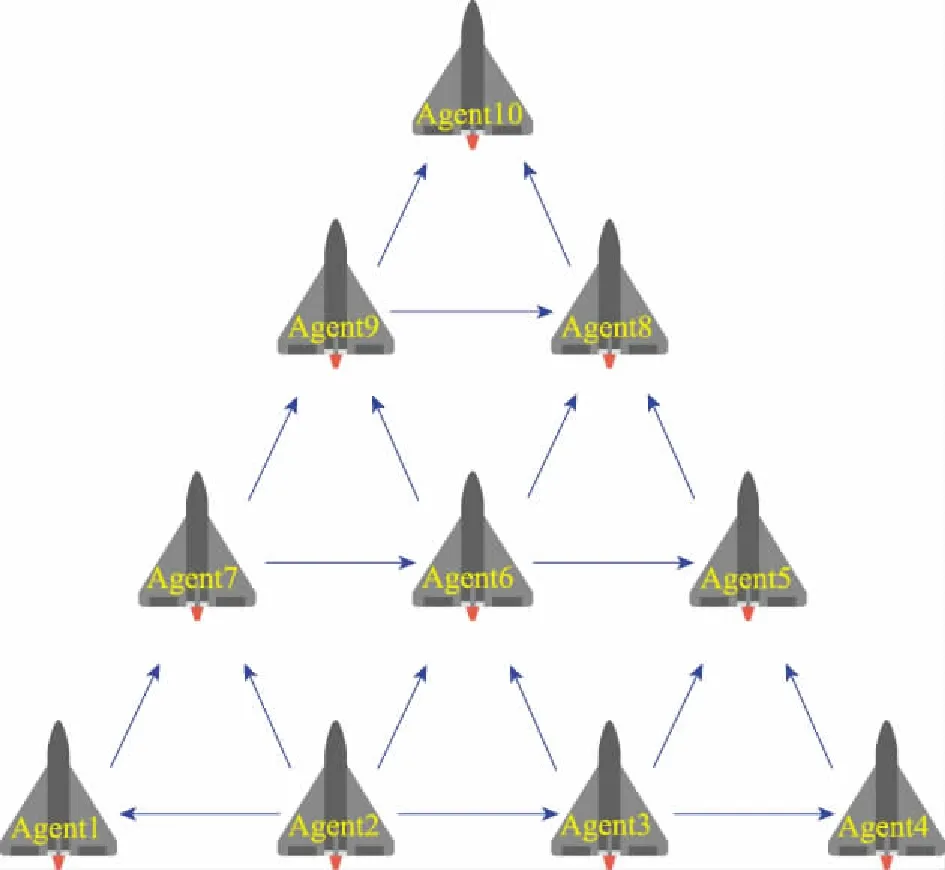
图1 多智能体系统网络拓扑结构图(N=10)Fig.1 Multi-agent systems network topology diagram (N=10)
多智能体系统在执行器故障情形下编队飞行过程中,需要彼此之间进行信息的交互与共享,才能实现协同飞行。根据第21节图论知识,智能体#与智能体#之间信息存在信息的交互,则邻接矩阵中的元素(,)=1,2,3,…,10取值取决于它们之间的方向,即=1,否则=0。基于此,可得邻接矩阵和度矩阵:

于是,进一步可得拉普拉斯矩阵=-。同时,设定每个智能体的质量=10 kg,每个智能体的集结速度=2 m/s,集结的角速度=59°/s。期望的参考轨迹=2 cos,=98 m/s。此外,选取=002,根据式≥(2),可取=002。控制参数可选取为=15,=20,=30,=25;=002,=004,=002,=002;=diag{3},=diag{10},=diag{5},=diag{8};====0005;同时需要逼近的两个参数为和,逼近的函数为,以及(,),重构函数(,)=(,5sin(15))。除此之外,多智能体系统的初始位置、线速度以及角速度,如表2所示。
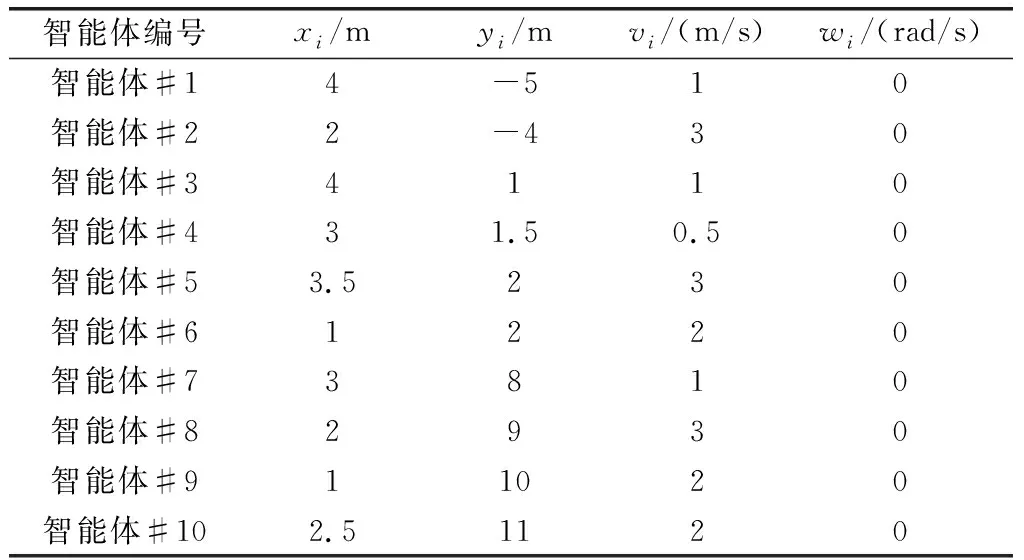
表2 多智能体系统的初始状态Table 2 Initial state of the multi-agent systems
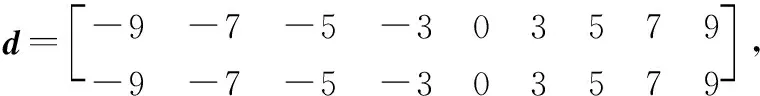
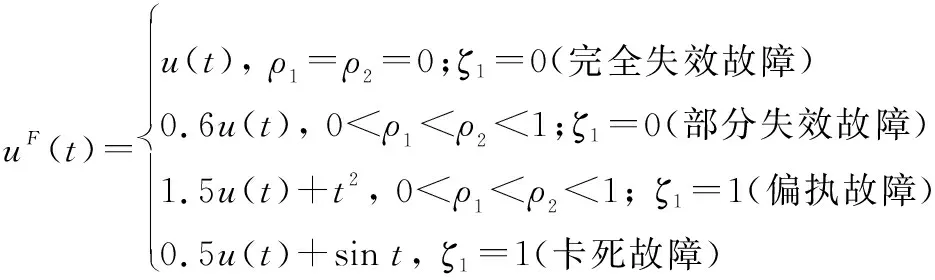
(56)
除此之外,在仿真过程中,考虑的两个算例,如下所示。
考虑以下非线性系统
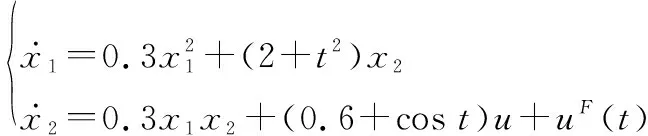
(57)
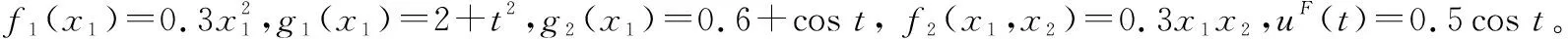
根据以上非线性系统、初始条件以及前述假设,其仿真结果如图2~图5所示。

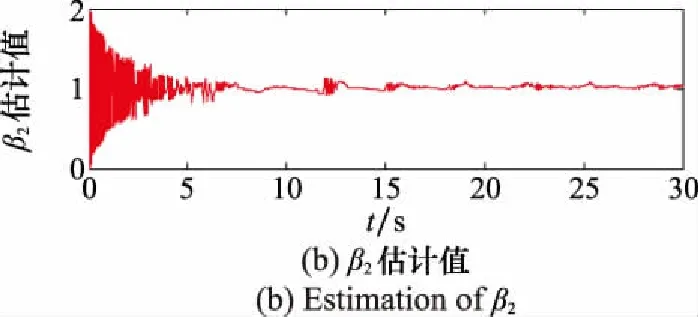
图2 控制参数β1和β2的估计值曲线图Fig.2 Estimation curves of control parameters β1and β2
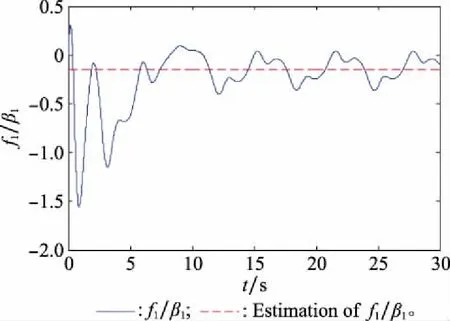
图3 f1/β1的神经网络逼近Fig.3 Neural network approximation curve of f1/β1
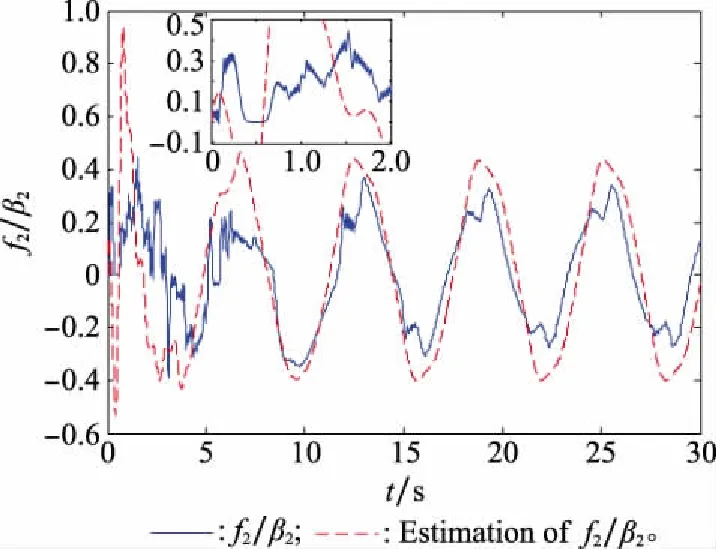
图4 f2/β2的神经网络逼近Fig.4 Neural network approximation curve of f2/β2
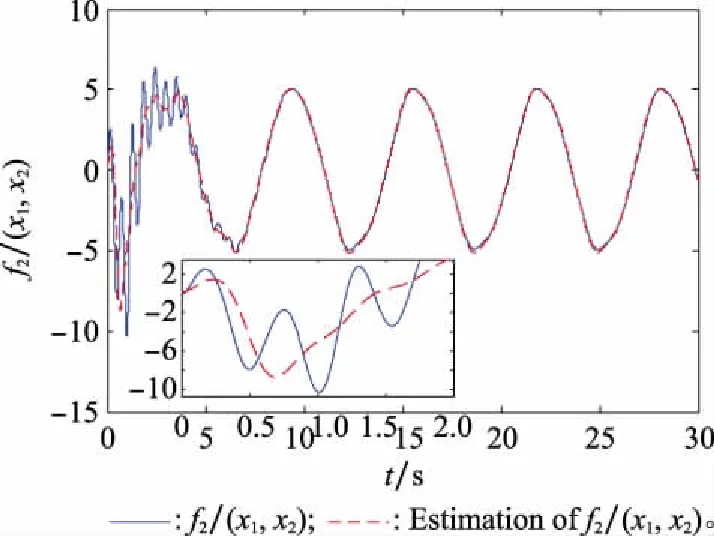
图5 f(x1,x2)的神经网络逼近Fig.5 Neural network approximation curve of f(x1,x2)
由仿真结果可知,所提出的RBFNNs可以有效逼近未知非线性项,使得在控制器设计过程中避免对高阶系统多次求导。而且,对含有执行器故障的多智能体系统,具有良好的容错效果。
为了进一步说明所设计的控制律的有效性,将其应用于由10个机器人组成的编队,进行容错控制研究,每一个机器人的动力学模型如下:
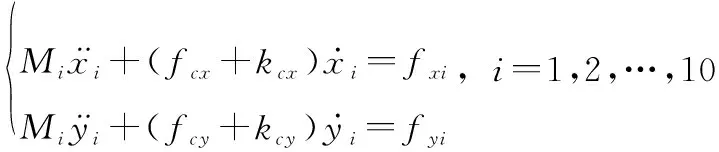
(58)
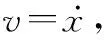
为了减少参数估计数量,作以下变换:
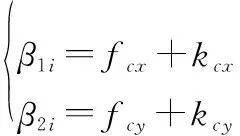
(59)
在本节中,采用相同的仿真环境,控制参数和初始条件,其仿真结果如图6~图9所示。

图6 机器人编队运动轨迹曲线图Fig.6 Trajectory curve of robot formation
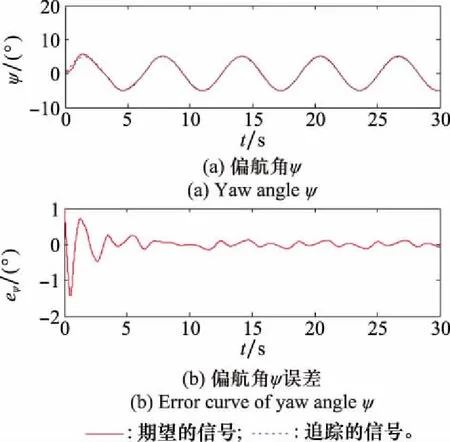
图7 机器人偏航角及其误差曲线图Fig.7 Yaw angle and error curves of the robot
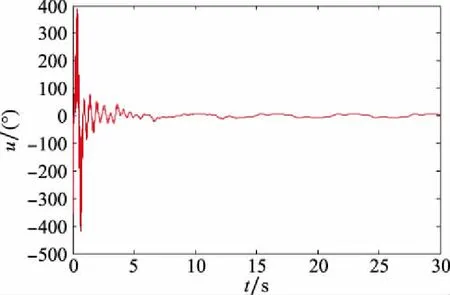
图8 机器人#1控制输入信号u变化曲线图Fig.8 Control input signal variation u curve of robot#1
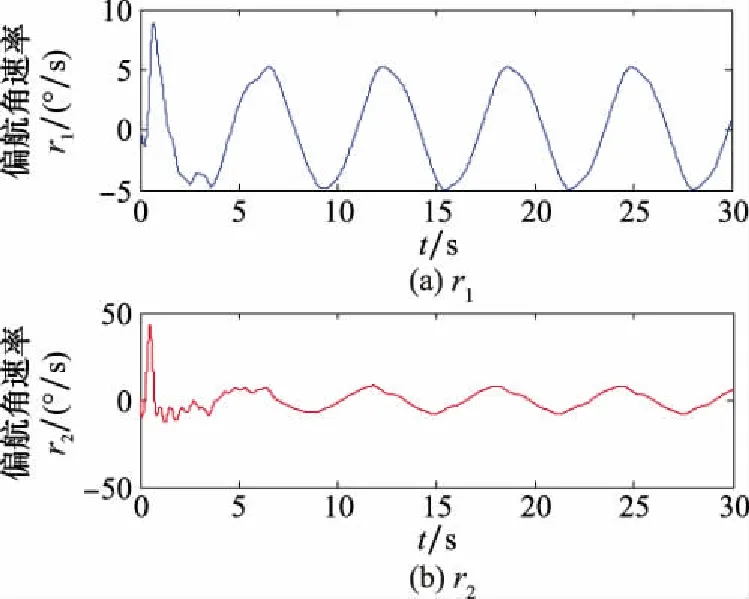
图9 机器人#5在控制参数β1和β2的偏航角速率r1和r2的变化曲线图Fig.9 Variation curves of the yaw rate r1 and r2 of robot #5 in control parameters β1 and β2
由仿真结果可得,所提出的控制方法,能够提高具有执行器故障的多机器人编队的容错能力,同时也能够有效实现其追踪运动目标的目的。此外,所提出的控制方案,能够使得机器人编队系统在整个追踪过程中,具有良好的容错效果。
6 结 论
本文提出了一种基于RBFNNs的动态面协同容错控制方法,能够有效解决故障情形下系统参数不确定以及系统瞬态不稳定问题。首先,利用RBFNNs对系统模型中的未知光滑非线性函数进行了实时估计。其次,采用反推技术与动态面技术相结合,设计了容错控制器,该控制器能够在执行器发生卡死故障和部分失效故障与外部干扰作用下实现多智能体的稳定控制,并保证智能体之间的一致性。随后,利用有限时间理论,实现了系统在预设时间内快速恢复稳定性能的需求。下一步的研究方向聚焦于以下两个方面:带有恶性攻击下的多智能体系统协同一致跟踪控制研究;基于弹性事件触发机制下带有恶意攻击的多智能体编队系统的协同容错跟踪控制研究。

