卫星网络时隙分配算法与路由规划优化
王瑞松, 马若飞, 王 琦, 钟志聪, 刘功亮,*, 张 杨
(1. 哈尔滨工业大学(威海)信息科学与工程学院, 山东 威海 264209;2. 北京跟踪与通信技术研究所, 北京 100094;3. 航天东方红卫星有限公司, 北京 100094)
0 引 言
相对于地面网络,卫星网络具有覆盖面超广、速度快等独特优点。尽管卫星网络建设费用昂贵,但因其具有独特的优势而一直备受关注。一方面,虽然5G网络正在不断完善,但边缘地区以及海上用户服务一直没能得到很好的解决。因此,为了进一步提升用户的服务质量,一些学者提出了星地一体化网络来解决这一问题。另一方面,卫星网络与人们息息相关并且已经应用到生活中的方方面面,如导航服务、地球观测、深空探测等。因此,研究高效的卫星网络信息传输方法是非常重要的。然而,对卫星网络的研究也存在着一些挑战。
(1) 网络的动态性。每个卫星都按照自己的轨道进行周期性的运动,因此卫星之间的相对位置是动态变化的,也就是网络拓扑是时变的。考虑到地球的遮挡,这种动态性会影响到卫星间的可见性,从而使得链路被迫中断,进而对网络性能产生巨大影响。
(2) 资源的限制性。卫星网络的资源相比地面网络是极其匮乏的。受限的资源包括能量、轨道、频率、天线数目等。如何充分利用有限的资源来完成高质量的服务是一个值得研究的问题。
正如上面所说,卫星网络拓扑的动态性刻画一直是当前研究的重点。作为新兴的方法,时间演化图是当前最有效的工具之一。文献[7]提出了小卫星网络的资源冲突分析框架。首先将卫星网络周期划分为多个时隙,每个时隙假设网络拓扑是不变的。此时,每个时隙的网络拓扑可以相应地转换为一个静态图。然后,考虑到卫星网络“接收-储存-转发”的特殊机制,引进了储存弧将每个时隙的静态图连接起来,从而形成一个整体的网络拓扑图。利用时间演化图,文献[8]和文献[9]分析了卫星网络中的任务调度问题,包括卫星建链与任务路由等问题。尽管时间演化图对于动态网络拓扑的处理取得了很好的效果,但是该方法难以面对长时间的拓扑变化。这是由于图的规模随着时间而不断增加。为了降低图的复杂度,文献[10]提出一种时间聚合图的方法。虽然图的规模始终固定,但是网络的拓扑变化通过边上的权重来刻画。边上的权重不再是一个数值,而是一个关于时间序列的向量,每个节点也赋予一个向量来刻画每个时隙卫星的储存能力。相比于时间演化图,时间聚合图的复杂度降低了,但一些图论知识并不能直接应用。对于一些经典问题,如最大流问题,一些新的求解方法需要进一步研究。因此,文献[10]和文献[11]分别研究了“单源单目的”和“两源两目的”两种场景下最优任务流分配算法。
前面的工作在动态网络拓扑处理方面已经做出了先锋性的工作,接下来重点研究的问题则是如何优化网络拓扑,也就是如何更好地规划星间链路的建立以便于提升网络的性能。一些学者针对不同的应用场景已经进行了初步研究。在文献[12]中,作者提出了一个理论模型用来估计两个地面用户之间的星间链路的跳数,并且给出了跳数的空间分布特性。文献[13]提出了一个协作方案,允许卫星在与地面站接触之前使用星间链路作为辅助方式来卸载数据。这样卫星将根据它们与地面站接触的时间长度合理地分配数据量。在文献[14]中,作者研究了星间链路卫星导航网络中的应用,并且在全球导航卫星系统精确定轨的测距约束下优化了网络时延与吞吐量。文献[15]考虑了地球自转和平面间相位差,给出了一种优化的星间链路建立方法来最大化可用链路。一些学者还研究了星间链路在卫星光网络中的应用。文献[18]研究了一种基于编码辅助技术的全球导航卫星系统星间链路自适应窄带干扰抑制方案,从而保证星间链路的可靠性。因此,星间链路的优化是十分必要的,这也促使了本文的研究。
对于给定的网络拓扑,路由协议设计则是影响网络性能的关键因素。然而,随着卫星网络规模的不断增大和任务类型的复杂性越来越高,路由问题也面临更多挑战。为了克服这些难点,各种先进的路由技术被研究。例如,文献[19]采用了一种时态网格模型来描述大规模网络的时变拓扑。然后,取代了传统的坐标定位方法,卫星可以通过网格来进行定位。文献[20]提出了一种基于网络编码的协同路由方法。通过编码的方法,数据可以通过多条路径协同传输从而加快传输速度。文献[21]提出了联合路由和调度的跨层机载处理设计,推导了联合分组路由和波束调度的最佳策略。文献[22]分析了“存储-转发”模式下最优路由的计算复杂度,证实了获得最优路由是十分困难的。文献[23-25]从能量的角度设计了路由算法。文献[26]用增强学习的方法求解了多目标路由规划。文献[27]则研究了超大规模卫星网络下的路由分发机制。文献[28-30]从服务质量、实时性以及安全性的角度对路由方案进行了研究。
综合上面的分析,本文研究了星间链路规划和路由规划。首先,利用时间演化图的方法,将卫星网络的动态性变化刻画在一张静态图上。然后,着重考虑卫星网络的资源限制条件,提出一种基于最大加权匹配的建链方法。为了降低求解算法的复杂度,利用拉格朗日松弛法来设计一个低复杂度的分布式算法。然后对于给定建链方法,设计不同优先级任务的路由规划。从仿真结果来看,通过提出的算法得到的解与最优解基本没有差别。
1 系统模型
本文考虑了一个一般的动态卫星网络,包含多个轨道,每个轨道上又分布着多个卫星,用来覆盖全球的区域。假设整个卫星网络由个卫星组成。由于卫星的轨道是确定的且卫星的运转是周期的,因此卫星网络的拓扑变化也是周期的。所以只需要研究卫星网络在一个周期内的拓扑状况就可以了,也就是[0,]。
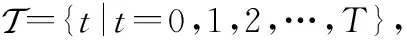
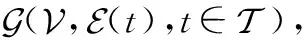
图1给出了卫星网络时间演化图的具体例子。其中红色的弧表示储存弧,黑色的表示链路弧。由于链路弧是双向的,在演化图中两个节点之间的建链是对称的。储存弧是单向的,表明数据只能从当前时隙储存在下一时隙,而不能反向为之。具体地,假设源节点为第2个节点,目的节点为第5个节点,所有边权重都一样。通过最短路径算法可以得到最优结果为第2个节点首先传到第4个节点,节点数据在第4个节点缓存一个时隙,接着下一时隙第4个节点传到第5个节点。
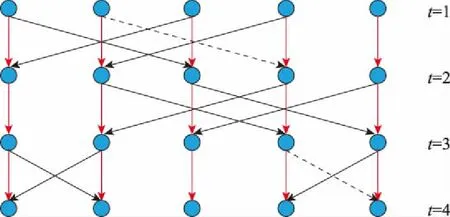
图1 卫星网络时间演化图Fig.1 Time evolution graph of satellite network
2 算法设计
2.1 基本约束
首先,考虑网络中的数据流在每个网络节点的流通情况。对于给定的时间扩展图,由于卫星网络中的数据流通采用的是“接收-储存-转发”的机制,因此对于每个时隙而言,每个卫星接收到的数据量加上上一时隙缓存下来的数据量应该等于当前时隙发送出去的数据量加上未发送而储存在该节点中的数据量。因此,可以给出以下约束:
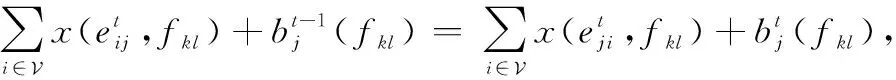
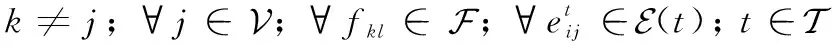
(1)
对于任务的起始点来说,任务的发出总量应该等于当前时隙任务成功发送出去的数据量加上储存在节点的数据量,具体地,
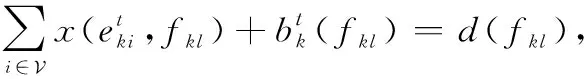
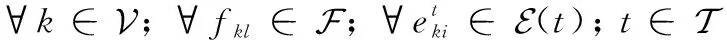
(2)
对于任务的目的节点来说,任务只允许到达目的节点并存储,而不允许再次发送,因此需要将目的节点的发送量设为0。
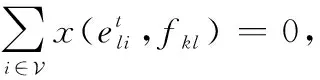
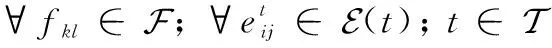
(3)
根据前文叙述,由于资源的限制,对每个时隙而言,即使每个卫星可能与多个卫星可见,但是每个卫星只能与一个卫星进行建链。即
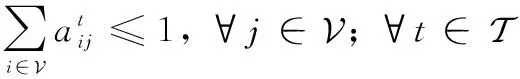
(4)
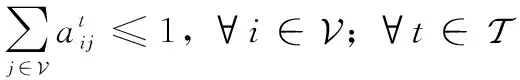
(5)
考虑到网络传输机制的特殊性,每条链接都是一个双向链接。相应地,在图中也就是无向边。因此,有如下约束:
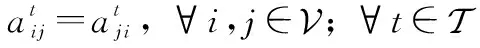
(6)
然而,考虑到链路资源的限制,对于给定的时隙,如果两个节点建立链路,则传输的总数据量不能超出链路最大传输能力;如果两个节点没有建立链路,则不能传输数据。对于这一限制,可以通过如下约束来表示:
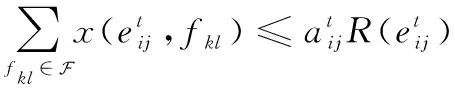
(7)

2.2 目标函数与模型

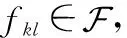
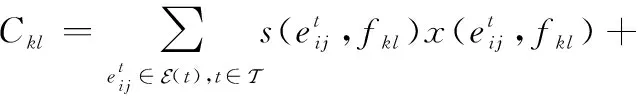
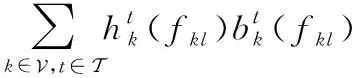
(8)
本文致力于一个公平性的资源分配规划,也就是最小化每个卫星节点花费的最大值。

(9)
通过上面的叙述,最终的优化问题可以表示如下:
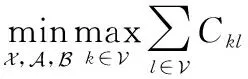
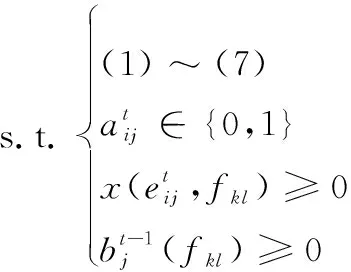
(10)
通过上面给定的变量与约束条件,最终将卫星网络中资源分配优化问题建模为一个整数线性规划问题。这样一个优化问题的求解是十分困难的。穷举法是处理整数规划的一个可行方法,但是穷举法的求解复杂度为指数复杂度,仅对于规模较小的整数规划是很有效的。对于上述的大规模优化问题而言,即便是能够将最优解找出,付出的计算代价也是十分大的,并且计算时间过长从而难以满足实时性的要求。因此,计算才是该问题的最大难点。为了保证在实际应用中的可行性,本文将原问题分解为两个子问题,分别为时隙分配方案设计与路由规划设计。虽然这并不是等价的转化,但是分解后的求解效率显著提升。
3 时隙分配方案设计
本节将上面的整数线性规划问题分解为两个问题,分别为时隙分配方案设计与路由规划设计。对于时隙分配方案,本节采用了最大加权匹配与拉格朗日松弛相结合的方法来设计低复杂度的算法。
本文提出的算法充分利用了卫星网络拓扑的已知因素,包括星间可行性关系、轨道、星间距离等。在初始阶段,通过地面站或者高轨控制卫星将网络的全局信息发送给每个卫星。然后,每个卫星可以独立地运行提出的算法,计算出整个网络的时隙分配结果,并且所有卫星计算的结果都是相同的。将当前计算的结果作为下一次算法运行的初始条件,则算法可以一直运行下去,并能保证所有卫星的同步。通过这样的方式就可以实现网络的全局控制而不需要特意的控制器。
3.1 基于匹配理论的方案
对于卫星系统时隙分配而言,一方面,在每个时刻,给定卫星可见性分析表,尽管每颗卫星可能与多个卫星可见,但每颗卫星仍然只与一颗卫星建立链接;另一方面,由于数据的发送通常需要多跳才能到达,而每个时隙最多只能完成一跳传输,网络中数据传输的性能要求往往取决于多个时隙的联合分配结果。
根据上面的模型与问题分析,可以看到时隙分配方案在一个周期内是相关的。每个时隙的匹配结果不仅受到之前时隙的匹配结果的影响,而且将影响到后续时隙的匹配结果。然而,对于一个长周期内的时隙分配而言,直接求解是十分复杂的。因此,有必要将问题的求解在时间上进行分解。
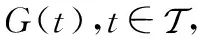
给定一个无向图,如果存在一个子图⊂使得图中每个节点只与一个节点相邻,则称其为一个匹配。如果||最大,则称其为最大匹配。其中||表示图中边的总数目。
然而,最大匹配仅仅能保证每个时隙卫星之间尽可能建链,但是不能保证网络数据传输的性能。因此,为了保证数据传输的性能,需要介绍最大加权匹配的概念,通过对每个边进行赋权来尽可能达到数据传输的一定性能。最大加权匹配的概念如下。
给定一个无向图,如果存在一个子图⊂使得图中每个节点只与一个节点相邻,则称其为一个匹配。如果图的总权重值最大,则称其为最大加权匹配。
对于最大加权匹配,下面给出一个图来展示具体的流程。如图2所示,根据网络的可见性分析,首先建立网络的拓扑连通关系,然后根据一定的规则,对每条边进行一定的权重设置。当权重设置完毕之后,通过特定的算法求解最大加权匹配,得到最终结果。
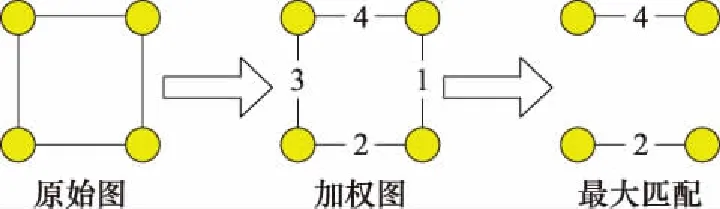
图2 最大加权匹配流程图Fig.2 Maximum weighted matching flow chart
图2中的最大加权匹配主要涉及到两方面的内容,分别为权重的设置和最大加权匹配的求解。对于权重的设置而言,考虑到每个时隙的匹配具有时间相关性,为了将时间上的耦合分解,这里将时间上的相关性转换到权重的设置上,从而实现时间上的分离。也就是说,当前时隙每条边权重的设置要根据之前时隙的边匹配情况来设置。下面将描述具体的赋权规则。
3.2 权重设置规则
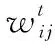
(1) 持续建链规则。如果上一时隙卫星节点没有与其他节点进行建链,则在上一时隙卫星所储存的任务就会有一定程度的堆积。考虑到这种情况,这里采取了一种补偿机制,也就是这类卫星节点优先与其他节点建立链接, 则权重赋值数学表示如下:
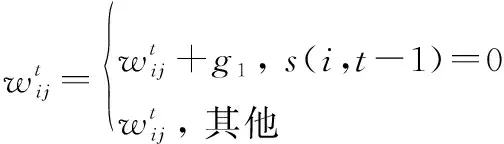
(11)
(2) 不重复链路建立。如果两个卫星上一个时隙或在一定时间内已经建立过通信链路,则在当前时隙倾向不再重复建立链路。这是因为不同数据的目的节点也是不同的,更换链路有助于保证资源分配的公平性,避免某一数据长时间等待。因此,对于重复的链路,在边的权重赋值上进行减少,在规定的时间内,建链次数越多,则权重越小。最终权重赋值数学表达为
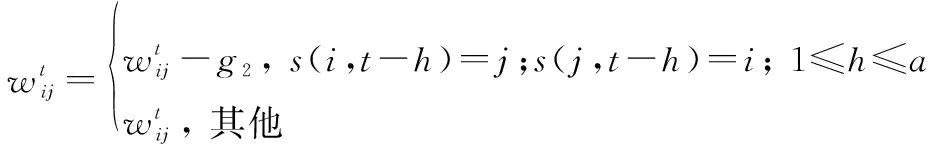
(12)
式中:是一个正常数,表示时间的范围。
(3) 跨轨道建链。网络中卫星分布在不同的轨道上,每个卫星都需要向其他所有卫星发送信息。为了保证信息能够均匀地发送,卫星建链对象应该考虑轨道之间的差异性。为了尽可能使网络连通,给定上一时隙卫星匹配对象的轨道,则在当前时刻卫星旨在与其他轨道的卫星进行建链。具体的权重赋值规则表示如下:
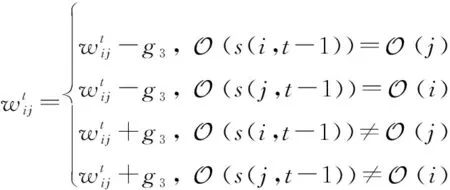
(13)
(4) 短距离建链。这一权重赋值在时间上并没有相关性,仅仅考虑网络传输的可靠性,即卫星之间相同情况下以短距离传输为准则,则权重赋值数学表示如下:
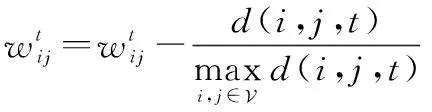
(14)
式中:,,是正常数,表示权重更新步长。上面4个链路加权规则可以分为3个优先级。其中,持续建链规则为第一优先级;不重复链路建立规则和跨轨道建链规则为第二优先级;短距离建链规则为第三优先级。在持续建链规则中,如果上一时隙卫星节点没有与其他节点进行建链,则在上一时隙卫星所储存的任务就会有一定程度的堆积。因此,为了公平性原则,务必要保证卫星在当前时隙成功建链。所以,在持续建链规则中的权重更新步长是比较大的,以此来体现其高优先级。对于两个第二优先级的规则,从本文的角度来说,两者并没有什么特别的差异性。这两个规则本质上都是保证卫星建链的多样性。因此,将这两个规则设为同一优先级。对于处在最低优先级的短距离建链规则,这个规则的设计初衷是防止出现两个相同的权重值。原因是相同的权重值在问题求解时会导致多个解的产生。对于相同权重值的情况,我们倾向于短距离的链路,因为这样的链路通常通信质量更有保障。因此,考虑到优先级的差异性,在最终确定权重的时候只要保证一个原则即可,那就是第一优先级的权重更新步长要大于第二优先级的权重更新步长,第二优先级的权重更新步长要大于第三优先级的权重更新步长。也就是说,要满足>>1,>>1。
3.3 基于拉格朗日松弛的求解算法
通过上面的赋权规则,已经对每条边上的权重做了设置,整个时隙分配问题可以转化为每个时隙上的一个最大加权匹配问题。对于这样一个问题,本文采用了基于拉格朗日松弛的求解方法,设计了一个低复杂度的算法。
最大加权匹配问题可以建模为一个0~1线性规划问题。具体地,给定当前时隙演化图中边的权重,则最大加权匹配问题可以转化为如下优化问题:

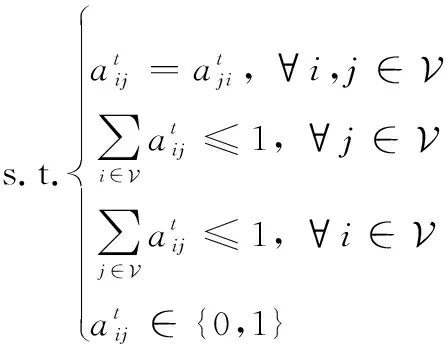
(15)
对于这样的一个整数线性规划,虽然最优解可以通过分支定界法来求得,但是求解复杂度极高。因此,本文采用拉格朗日松弛的方法设计一个低复杂度算法并求得一个次优解。

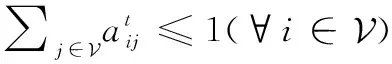

证毕
根据以上说明, 优化问题(15)等价于如下问题:

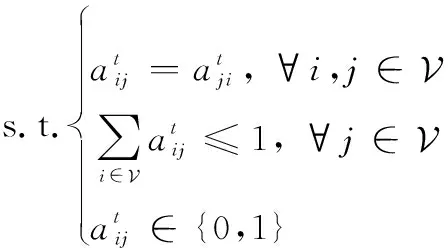
(16)
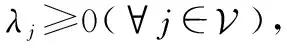
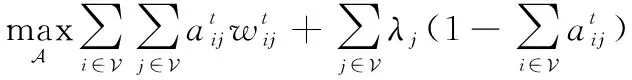

(17)
将问题进行整理可以得到
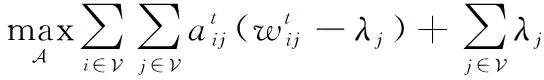
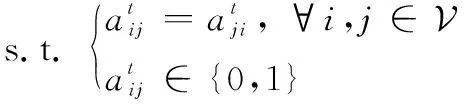
(18)
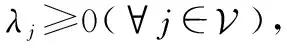
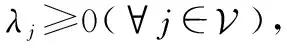
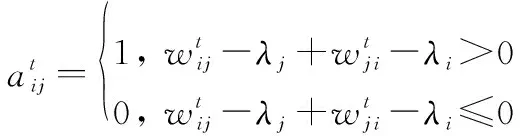
(19)
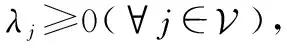
证毕

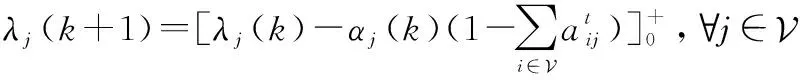
(20)
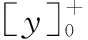

(21)
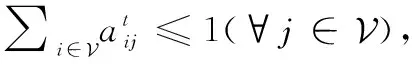
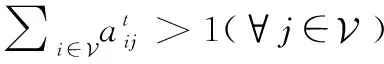

(22)

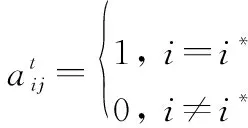
(23)
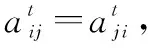
通过上面的置零操作,已经得到了一个可行解。但是,这个可行解里面可能存在多个未匹配节点。因此,为了进一步提升性能,可以对未匹配的节点进行一次检测,重新再做一次匹配。具体地,从得到的解中提取出与任何节点都没建链的节点集合,记录彼此之间的权重值,构成新的权重矩阵。执行上面的步骤求得新集合的最大加权匹配结果,将匹配结果添加到原来求解的结果中去。如果还有未匹配的节点,则继续执行上面的步骤,直到最终匹配结果不再改变。具体的内容可以参考下面的算法1。

算法 1 时隙分配求解算法1. 输入:初始的权重矩阵, 拉格朗日乘子, 时间长度T, 最大迭代次数Imax, 门限值ε, 卫星可见性分析表。2. 输出:每个时隙的卫星匹配建链表##拉格朗日松弛算法求解过程(3~15行)3. 根据式(11)~式(14)更新权重矩阵4. fort=1:T5. fork=1:Imax6. 根据式(19), 计算时隙分配结果7. 计算问题(17)中的目标函数值F(i)8. if |F(k)-F(k-1)|/F(k)<ε9. 停止迭代10. else11. 根据式(20)更新拉格朗日乘子12. end13. end 14. 根据式(22),计算新的权重矩阵β15. 根据式(23),对结果进行处理##优化解提升过程(16~22行)16. while存在卫星尚未匹配17. 对权重矩阵,删除已匹配卫星对应的行与列,形成新的权重矩阵18. 执行步骤3~步骤15, 获得新的匹配结果,更新匹配表19. if匹配表不再变化20. 跳出循环,输出最终匹配表21. end22. end23.end
3.4 算法分析
从算法1可以看出,对于给定的时间长度,所提出的算法是对每个时隙进行求解的。对于每个时隙而言,总共的变量数为个,其中为卫星数目,对于每一次的迭代,只需要对每个变量进行直接更新就可以,且算法在有限步内收敛,因此每个时隙的求解复杂度为(),整个算法的复杂度为()。
提出的时隙分配算法主要应用了卫星网络拓扑的可预测性。尽管卫星网络是动态变化的,但是它与普通的时变网络是不同的,由于轨道是固定的,卫星每时每刻的位置都是可以提前计算的。算法的实际应用可通过两种方法实现。第一种方法是地面站将一段时间内的时隙分配结果提前计算好,然后将其发送给每个卫星。这样虽然会增加卫星通信成本,但是增加不是很显著,这是因为一段时间内只需要通信一次即可。另一种方法是每个卫星独立地执行相同的算法,不需要进行信息的交换与收集就可以得到相同的结果。采用这个方法不需要任何通信成本,但是每个卫星需要付出计算成本。
4 延迟最小化的路由方案
4.1 路由算法设计
通过上面的时隙分配方法,可以得到每个时隙各个卫星的建链情况。然后,通过储存弧,可以将一个周期内动态图转化为一个静态图。在知道网络全局信息的前提下,多个信息流的路由规划可以通过求解一个大型线性规划来得到相应的路由。然而,对于卫星网络而言,每个卫星都掌握整个网络的全局信息是十分困难的。相反,每个卫星通常只知道临近卫星的信息或者不知道任何卫星的具体信息。
给定网络拓扑图,对于单个的任务流,其路由问题可以转化为网络中的最短路径问题。 Dijkstra最短路径算法是求解单源单目的数据流的一个最优路由算法。给定每条路径的权重,Dijkstra算法即可在多项式复杂度内找到从源节点到目的节点的最优路径。
本文考虑以延迟作为每条路径的花费。因此,根据前面提出的网络模型,定义每一条边的权重为当前链路的传输时延:

(24)
对于每个数据流来说,由于链路容量限制,不一定在同一时隙全部到达目的节点。因此对于每个节点,还需要设置一个虚拟目的节点,用来连接每一个时隙的节点。此虚拟节点与每个时隙对应节点进行建链,每条链路的权重设置为0,表示该数据流在任意时隙到达都可以。另一方面,考虑到不同的数据流之间是有差异性的,先入先出的规则不再适用,而改为高优先级数据先出,低优先级数据后出。数据的优先级是根据业务的类型来确定的。例如,卫星网络中支持的业务包括自主导航业务、遥测回传业务、全球短报文业务、其他扩展服务业务等。与之对应,星间链路支持传输的数据类型包括:自主导航数据、遥控数据、遥测数据、确认数据、扩展应用数据、备用数据类型等。这些数据的服务质量要求也不完全相同。像导航业务这种对实时性要求很强的通常优先级较高,需要尽快传输。而像一些长期观测业务则对实时性要求不强,只需要能够最终能够准确传到目的地即可,因此这类业务优先级则较低。
当一个数据流产生时,源节点首先为每个数据根据其优先级依次进行路由规划。然后,每个数据按照相应的路由进行发送。然而,当卫星节点发送数据的时候,由于链路弧容量有限,不能保证所有的数据都能在此时隙成功发送。当产生拥塞时,高优先级的数据首先进行发送,剩余的低优先级的数据由于当前时隙发送失败从而导致原来的路由不再适用。为了保证剩余的缓存包能够成功发送出去,则当前的卫星节点必须为它重新规划路由。为了保证数据的成功发送,卫星接收到的数据包应该包含以下基本信息:基本数据,目的节点,数据包长度,初始路由,优先级等。具体的步骤可以参考算法2。

算法 2 不同优先级数据包的路由算法1. 输入:时隙分配表, 数据包基本信息2. 输出:每个数据包的路由表3. 检测当前节点中缓存中的数据, 选取出当前时隙可以发送的数据4. 将这些数据包按照优先级从高到低排序, 并假设总数目为M,包的长度为p(m)5. form=1:M6. ifC>p(m)7. 准备发送该数据包,更新链路容量C=C-p(m)8. else9. 该数据包进行等待, 重新规划路由10. end11. end
4.2 算法扩展
尽管算法2考虑了以延迟为目标的路由设计方案,但是该算法仍可以进一步扩展从而可以满足业务多样性的要求。主要从两方面进行扩展:一个是权重函数的设计;另一个为业务优先级的权衡。
首先是权重函数的设计,权重的设计根据目标的不同可以进行自适应更改,并不一定非要将延迟作为链路的权重。比如,将跳数作为评判链路的准则,权重的赋值规则就可以更改为
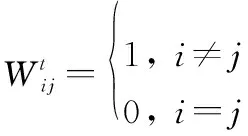
(25)
式中:≠表示数据要经过一跳来进行发送,因此将权值设置为1;而=表示数据将会缓存而等待下一个时隙发送,因此将权值设置为0。更进一步,一些业务对跳数和时延具有双重要求,则在权重设计时通过加权的方法兼顾考虑,通过设置权重因子的大小,自适应加权规则如下:
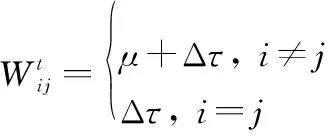
(26)
当业务产生的时候,卫星可以根据数据类型的不同,自适应地选择赋权规则,然后执行该路由算法。
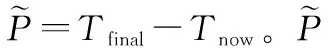
5 仿真分析
如图3所示,通过STK软件,本文建立了一个由32颗中轨卫星组成的网络。网络包含4个轨道,每个轨道上均匀地分布着8颗卫星。对于这样一个网络,卫星之间的距离比较大,通信成本比较高,不适合过多地进行信息交换。此网络正好适用于本文提出的低通信成本算法,因此本文将其作为代表来评估算法的性能。根据第2节的网络模型描述,卫星网络运行周期被划分为多个时隙,在每个时隙内,每个卫星至多与一个卫星建立链接。一旦链路建立,则链路一直持续到该时隙结束,单个时隙内不允许重新建链。在当前时隙,如果任务不能完全发送,则储存到本地储存器并等待下一时隙建链后发送或者继续储存。详细的参数设置请参考表1。
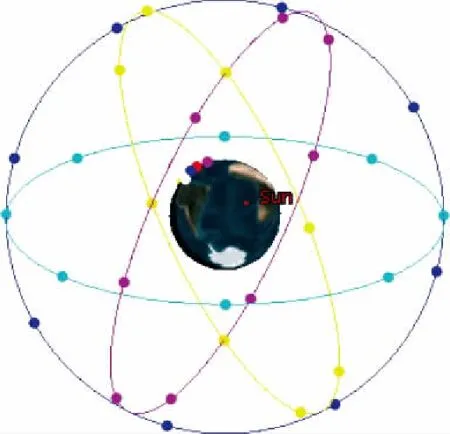
图3 卫星网络组成图Fig.3 Satellite network composition
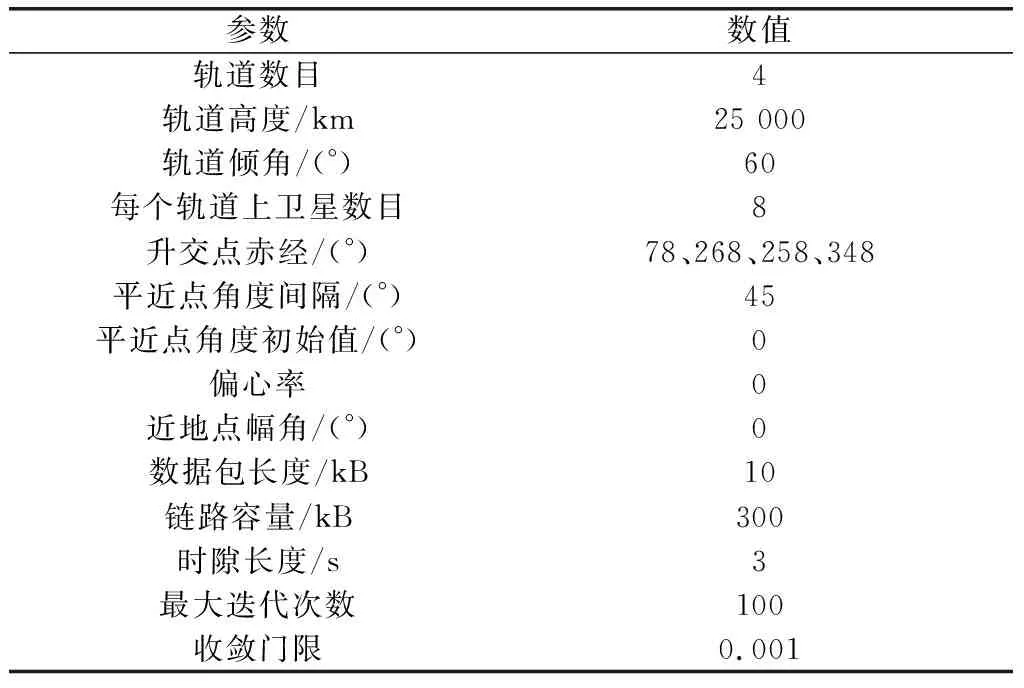
表1 仿真参数
为了展示提出算法的性能,在仿真时将本文提出的算法与对应的算法进行了对比。仿真图中的“基于拉格朗日松弛的方案”为本文提出的算法的性能,而“基于最优匹配的方案”是相应的对比算法。
基于最优匹配的方案采用整数规划算法(例如,分支定界法、枚举法等)求解对应的匹配问题式(16),因此得到的是一个最优匹配方案,其他部分与算法1和算法2的操作部分一样。
在图4和图5中,假设每个卫星都要向剩余的31个卫星传递相同优先级的数据。卫星与卫星之间发送的数据量为1~6数据包。图4和图5给出的是所有任务的平均时延和平均跳数。从图4中可以看出,平均时延随着数据包数量的增长而快速增长。原因是随着数据包数量的不断增长,同一时隙共同发送的数据增多。然而,链路容量是有限的,因此这就导致了数据发送时产生拥挤,一部分数据被迫只能暂时缓存在中继节点并重新规划路由,进而导致了任务时延的增加。另外,从图中可以看出,本文提出的“基于拉格朗日松弛的方案”与“基于整数规划的方案”具有相近的性能。
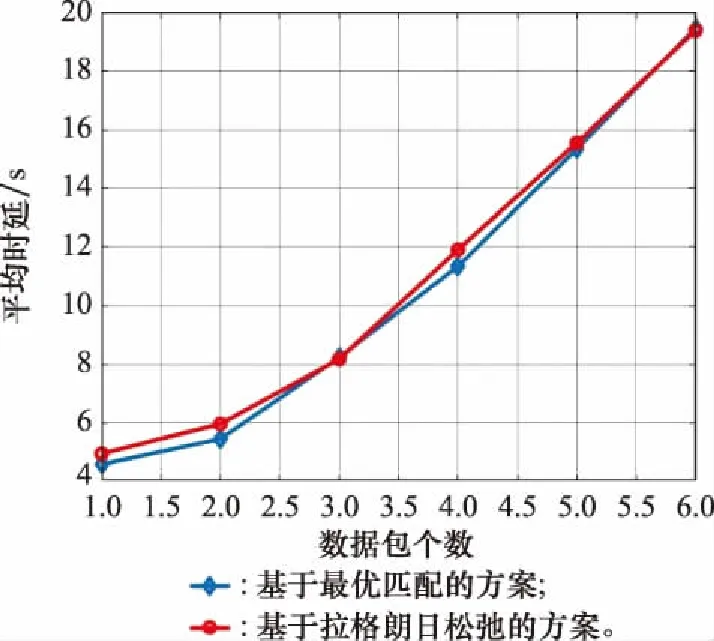
图4 数据包数目与平均延迟的关系Fig.4 Number of data packets vs delay
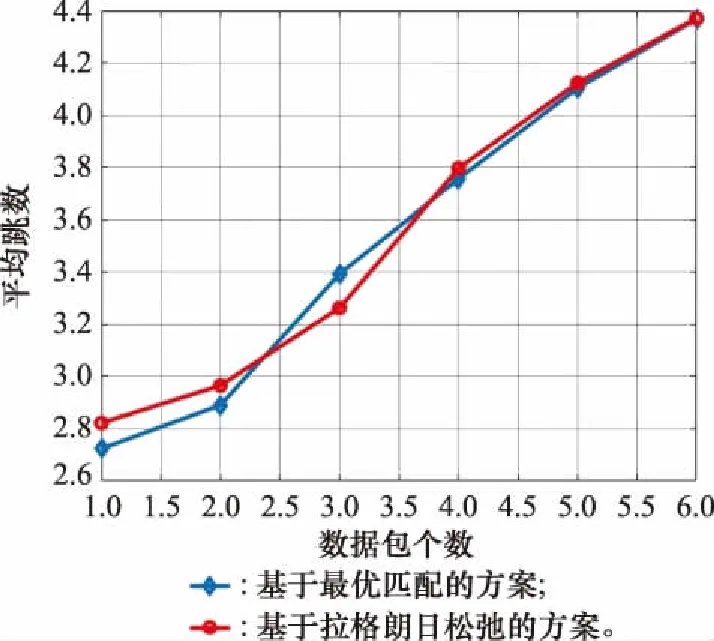
图5 数据包数目与平均跳数的关系Fig.5 Number of data packets vs average number of hops
与图5的场景基本相同,假设每个卫星都要向剩余的31个卫星传递相同优先级的数据,每个卫星发送的数据包个数分别为2和4。图6展示了缓存溢出比率与缓存容量的关系,其中缓存溢出比的定义如下:


图6 缓存溢出比与缓存容量的关系Fig.6 Overflow ratio vs storage capacity
可以看出随着缓存溢出比要求的不断降低,对卫星缓存容量的要求也不断降低。例如,当发送的数据包个数为2,缓存溢出比要求为0.1的时候,要求缓存容量为630 kB;而当缓存溢出比要求为0.3的时候,要求缓存容量为520 kB,下降了21%。另一方面,缓存容量还与整个网络中的总数据量息息相关。例如,当缓存溢出比要求为0.3的时候,对于发送2个数据包的情况,要求缓存容量为520 kB;而对于发送4个数据包的情况,要求缓存容量为1 250 kB,提升了1.4倍。
图7与图8分别展示的是不同优先级数据的平均时延与平均跳数性能。在这个场景下,每个卫星都要向其他31个卫星发送具有不同优先级的数据, 每个优先级数据包的个数为1。从图7可以看出,平均延迟随着数据优先级的降低而不断升高。这是因为高优先级的数据优先发送,当链路容量不足时,低优先级的数据被迫只能等待。所提出的“基于拉格朗日松弛的方案”与“基于整数规划的方案”具有相近的性能。
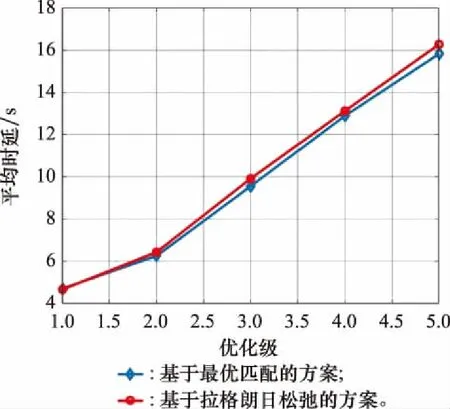
图7 不同优先级数据的平均延迟Fig.7 Average delay of data with different priorities
在平均跳数方面,根据图8,可以看出随着数据优先级的降低,平均跳数呈现先增加后减小的趋势。原因是对于高优先级的数据,享有绝对的资源占有权,因此可以随时发送,但是随着优先级的降低,数据必须为高优先级的数据让路,从而导致数据不断地切换中继卫星,进而使得跳数加大,最后,对于优先级极低的数据来说,由于链路容量限制,数据不得不一直在一个卫星中持续缓存,直到其他高优先级数据传输完毕,此时网络不再拥塞,数据可以直接发送,因此这一部分数据只会在延迟上增加,在跳数上并没有增加。
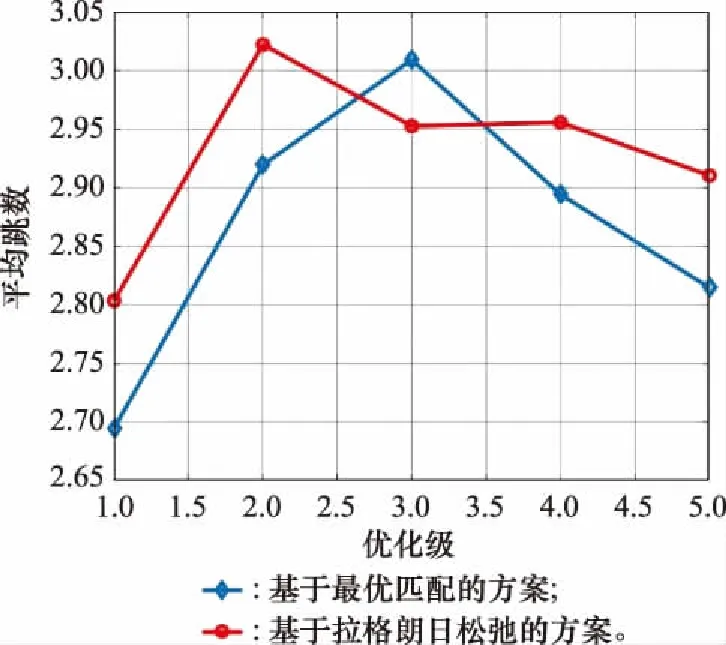
图8 不同优先级数据的平均跳数Fig.8 Average number of hops of data with different priorities
图9展示的是基于拉格朗日松弛的求解算法的收敛性,对比了通过整数线性规划求得的最优解与用拉格朗日松弛方法所得到的解的差异性。可以看出,拉格朗日松弛方法提供的是原问题的一个上界,通过不断迭代,逐渐逼近最优解。
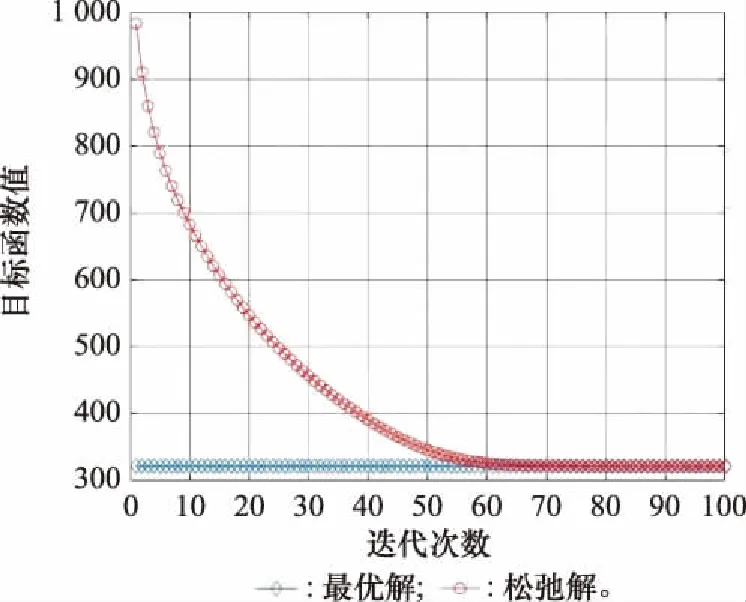
图9 算法1的收敛性Fig.9 Convergence of Algorithm 1
6 结 论
本文研究了卫星网络中的资源调度问题,包括时隙规划与路由规划。对于时隙规划,综合考虑轨道、距离、时间相关性等具体细节,致力于最大化网络的连通性,最终将其建模为最大加权匹配问题。为了减少问题求解复杂度,本文提出基于拉格朗日松弛的分布式算法来设计时隙规划。仿真结果表明,提出的算法与最优解之间的间隙几乎为零,从而展示了提出算法的有效性。基于给定的时隙规划,本文进一步考虑了多优先级业务的路由问题。仿真展示,高优先级业务传输时延较低,但在跳数方面没有太大的差别。

