生物组织多光谱偏振特性研究
乔文龙,周 亮,刘朝晖,龚勇辉,姜 乐,吕媛媛,赵鹤童
1. 中国科学院西安光学精密机械研究所,陕西 西安 710119 2. 中国科学院大学,北京 100049 3. 酒泉卫星发射中心63636部队,甘肃 酒泉 732750
引 言
偏振不同于光波的相位和振幅,是光波横波性的有力证明。 偏振光在生物组织中传播时,会根据不同散射体系的特征,呈现出相应变化规律。 在生物检测领域越来越多的使用偏振技术,如使用穆勒(Mueller)矩阵来检测皮肤组织是否发生癌变也逐渐趋向成熟[1-2]。
Borovkova等使用多波长穆勒偏振成像结合适当的图像后处理来检测组织中的恶性肿瘤[3]。
Valery等对偏振光与生物组织的相互作用进行了详细的研究[4]。 Zhang等研究了585 nm偏振光在生物组织中的传输特性[5],Valery与Zhang等都是针对单一波长的偏振光进行了研究。 随着计算机技术不断发展许多研究采用仿真方法来模拟光在散射介质中的传播。 Adam等使用一种分形传播方法(FPM)能够准确有效地模拟聚焦光束的衍射效应,以及组织中存在的散射、折射光束转向和光束焦点像差的微观不均匀性[6]。 Soichi Otsuki等仿真研究了偏振光在双折射混浊平面介质中的多次散射[7]。 Shen等使用MC方法仿真研究了相干光在散射介质中的传输特性[8]。 Periyasamy等在MC方法的基础上仿真研究了光线在生物组织中的传输过程[9]。 Zhou等使用MC方法对容积脉搏波(PPG)的光谱特性进行了仿真研究[10],对于偏振光在生物组织中的多光谱特性未说明。 Nozomi Nishizawa等使用MC方法对圆偏振光在伪组织和癌变组织中的散射过程实现了仿真研究[11]。
综上所述,大部分研究人员都只对单一波长、单一偏振态的偏振光在生物组织中的传播规律进行了研究,而对偏振光在生物组织中的多光谱特性研究较少。 为了阐明不同颜色、偏振态偏振光在生物组织中的传播特性,在上述学者研究的基础上,引入了四种典型偏振态和可见光及近红外光谱维度,以期实现对生物组织中光学传播特性更全面、精确的表征。
利用MC方法,对400~1 000 nm波段范围内的偏振光在散射介质中的传输特性进行了仿真研究,并结合实验得出结论,随着波长的增加线偏光经组织后向散射出射后的偏振度整体呈上升趋势,圆偏光呈下降趋势,但圆偏光后向散射出射后整体的偏振度要高于线偏光。 表明,圆偏光比线偏光在组织中传播时具有更好的偏振保持性,更强的传播能力,更能反映深层组织的生理信息。 该研究可为多光谱偏振生理信息获取及相关技术提供一定的理论支持。
1 理论基础
1.1 组织模型
光的散射主要与生物组织复杂的结构特性有关。 不同生物组织的尺寸分布如图1所示。 常见的组织成分如细胞外液的折射率为1.35~1.36,细胞质是1.36~1.375,细胞核、线粒体和细胞器是1.38~1.41,黑色素是1.6~1.7。 多数生物组织平均折射率位于1.34~1.62范围内。 其中细胞核和线粒体是主要的散射体[12]。

图1 生物组织的尺寸分布Fig.1 Size distribution of biological tissues
由于线粒体和细胞核的尺寸范围为1~10 μm,因此在仿真中设置组织模型中的散射微粒直径为a=2 μm,折射率为ns=1.59,背景介质的折射率设置为nb=1.33接近皮肤组织的微循环层,组织模型示意图如图2。
1.2 散射模型
瑞利理论(Rayleigh theory)和米氏理论(Mie theory)都是基于Maxwell方程建立的并用于描述平面单色光波被单个粒子散射的情形[12]。 瑞利散射理论主要适用于散射粒子尺寸远小于波长的散射事件,米氏散射理论更适用于一般性的散射。 米氏理论揭示了散射程度与散射粒子半径a、入射波长λ和相对折射率nrel之间的关系。 其中,关于尺寸参数和相对折射率的定义如式(1)
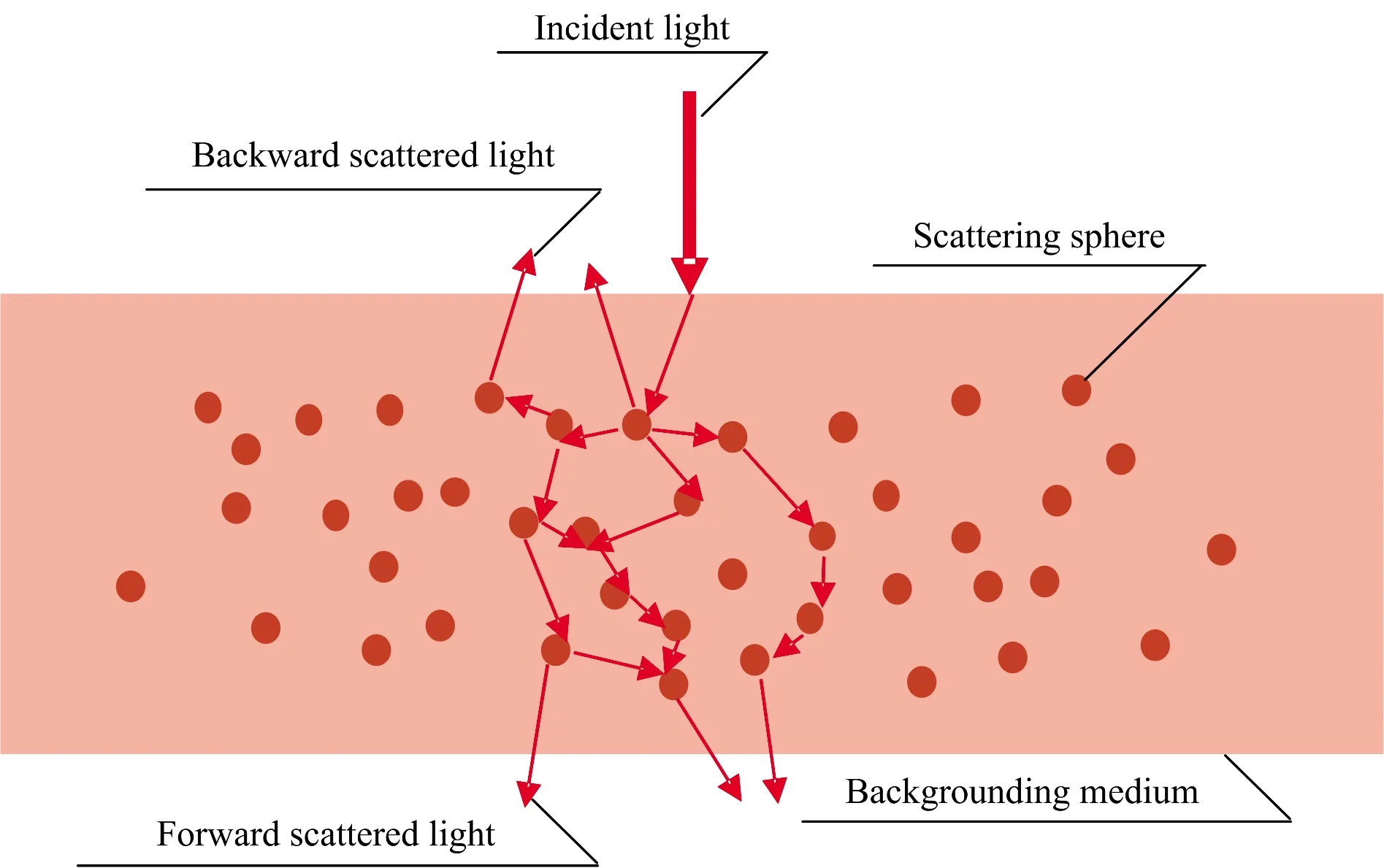
图2 单层生物组织模型示意图Fig.2 Schematic of single-layer tissue model
(1)
尺寸参数X是一个无因次量,当其小于1时,使用Rayleigh散射理论,瑞利散射理论的散射强度与散射角度和波长之间的关系由式(2)决定
(2)
式(2)中,Io为散射以后的出射光强,Ii为入射光强,θ为散射角(θ=0°为前向散射,θ=180°为后向散射),c0是体积为V的悬浮粒子浓度,r为散射颗粒到观察点的距离,α是半径为a/2的球体极化率,定义为
(3)
当微粒直径为20 nm,波长为600 nm时,尺寸参数X=0.139 28,此时散射的强度随散射角的变化规律如图3。

图3 单个微粒瑞利散射模型Fig.3 Rayleigh scattering model of single particle
从图3中可以看出瑞利散射具有前向和后向散射强度对称分布的特性。 由Mie散射理论可知在距离散射体r处的场点p的散射光强分布由式(4)决定。
(4)
I(θ,φ)=|S1(θ)|2sin2φ+|S2(θ)|2cos2φ
(5)
其中λ为入射光波长,I0为入射光强,Isca为散射光强,θ为散射角,φ为偏振光的偏振角。S1(θ)和S2(θ)为振幅函数。
(6)
(7)
其中an和bn为与贝塞尔和汉克尔函数有关的函数
(8)
(9)

(10)
(11)
在相同λ和nb条件下,将微粒直径尺寸扩大为500 nm,则尺寸参数X变为3.481,此时散射强度随散射角的变化规律如图4。

图4 单个微粒米氏散射模型Fig.4 Mie scattering model of single particle
从图4的模拟结果中可知米氏散射的散射光线展现出强烈的前向散射特性。
1.3 偏振光的表示
偏振光可以使用Jones矩阵、邦加球和Stokes矢量来表示,Jones矩阵只能表示偏振度为1的完全偏振光,对于偏振度小于1的偏振光无法完整表示;邦加球表示法涉及到相位信息的获取,虽然可以完整的表示偏振光,但由于在实际操作过程中很难保留相位信息,因此,该方法在实验中很少采用。 Stokes矢量包含四个元素,采用6种不同偏振态光线的强度信息来描述偏振光,可以表示任意一种偏振态的光线,易于实验测量。 Stokes矢量的定义如式(12)
(12)
式(12)中,IH,IV,Iπ/4,I-π/4,IR和IL分别代表水平线偏振光强度、垂直线偏振光强度、45°度线偏振光、135°线偏振光、右旋和左旋圆偏振光。I为总的光强,偏振度是描述光线偏振程度的物理量,多数偏振光往往是几种偏振态叠加的结果,Stokes矢量法对于偏振度的定义如式(13)—式(15)
(13)
(14)
(15)
其中DOP,DOLP和DOCP分别为偏振度、线偏振度和圆偏振度。
2 实验部分
2.1 Monte Carlo方法
Monte Carlo方法是一种基于概率统计的数学物理模拟方法,得益于计算机的计算速度和计算精度的不断提升,使得Monte Carlo方法在各个物理仿真实验中越来越多的被使用,尤其在生物医学领域、光学领域等。 该方法的仿真准确度取决于样本数量的大小,样本数量越大仿真结果越接近于真实现象。 本工作基于单个微粒散射理论,采用Monte Carlo方法模拟了100万个带有偏振信息的光子在前述生物组织模型中的传输特性。
2.2 多光谱偏振特性仿真
选择波段范围为400~1 000 nm包含了可见光和近红外部分,光谱分辨率为10 nm,散射微粒分布密度为0.01 particle·μm-3,仿真样品厚度设置为1 mm。 入射光线的偏振态为: 水平线偏振、垂直线偏振、45°线偏振和右旋圆偏振光。 如图5为偏振光经前述组织模型后向散射出射光偏振度随波长变化的仿真结果。
仿真结果表明不同偏振态的光线经组织后向散射出射后,其偏振态会发生改变,线偏振光(水平线偏振、垂直线偏振、45°线偏振光)随着波长的增大其偏振度整体上升,右旋圆偏振光随着波长的增加其偏振度整体下降。 同时,圆偏振光的偏振度整体要高于线偏振。 表明,圆偏振光在生物组织中具有更好的偏振保持性。
3 结果与讨论
实验选用白色LED灯为光源,用450, 525, 550, 590, 610, 650和690 nm滤光片进行滤光,两组线偏振片和右旋圆偏振片分别为起偏和检偏器用于改变光线的偏振态,彩色相机用来记录手掌的偏振图像。 由于仿真结果显示前述三种偏振态的线偏光偏振度变化与波长的关系较为接近,因此为了简化实验,仅以水平线偏振光和右旋圆偏振光来研究线偏光与圆偏光在生物组织中的传输特性,实验系统如图6。
入射光与探测器之间的夹角φs为21°。 光波可以分解成任意两个正交偏振波,根据能量守恒定律有
I=IH+IV=Iπ/4+I-π/4=IR+IV
(16)

图5 (a) 水平线偏振光,(b) 垂直线偏振光,(c) 45°线偏振光,(d) 右旋圆偏振光Fig.5 (a) Horizontally polarized light, (b) Vertically polarized light, (c) Linearly polarized light, (d) Right-handed circularly polarized light
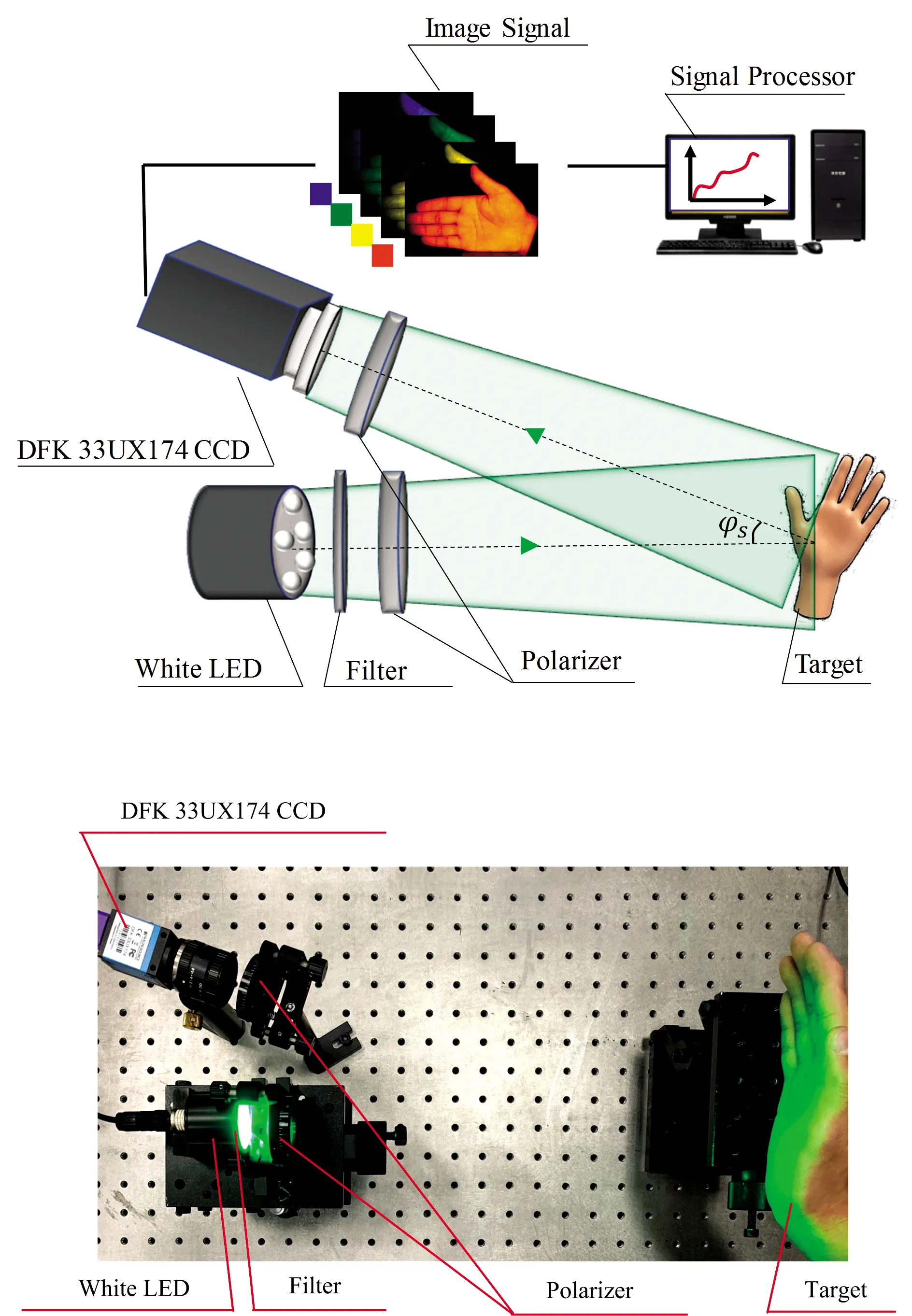
图6 实验系统Fig.6 Experimental system
则式(10)可以进一步写为
(17)
因此在实验过程中只需获取目标IH,IV,Iπ/4和IR的偏振图像即可实现偏振信息的斯托克斯矢量表示;强度I的计算由式(18)决定,N为像素数,IR,IG,IB分别为R通道、G通道和B通道的像素值。 实验结果如图7所示。
(18)
实验在避免了环境光干扰的情况下进行,图像尺寸为1 920×1 080像素,相机光圈数为16,曝光时间为33 ms。 利用前述方法对实验结果进行处理得到450~690 nm波段内水平线偏振光入射和右旋圆偏振光入射时偏振度随波长的变化情况如图8、图9所示,图8为水平线偏振光入射时后向散射光偏振度随波长的变化情况,图9为右旋圆偏振光入射时后向散射光偏振度随波长的变化情况。
从图8(a)和图9(a)中可以分别对比两种偏振态的仿真数据和实验数据,仿真得到的水平线偏振光偏振度在0.09~0.12之间,实验得到的水平线偏振光偏振度在0.13~0.26之间。 仿真得到的右旋圆偏振光的偏振度在0.63~0.67之间,实验得到的右旋圆偏振光偏振度在0.53~0.56之间。

图7 实验结果Fig.7 Experimental results

图8 (a) 水平线偏振光入射偏振度随波长的变化, (b) 归一化偏振度随波长变化Fig.8 (a) Variation of DOP of horizontally polarized light, (b) Variation of normalized DOP with wavelength
可见,仿真数据与实验数据本身存在差异,因为仿真数据属于理想近似,将复杂的生物组织进行了简化,而实际实验时影响因素较多,如采用的光源光谱特性、彩色相机的光谱响应和噪声、以及滤波片和偏振片的光学特性与理想值存在差异等导致仿真结果与实验结果在幅值上有所不同。 实验过程中利用Stokes矢量法计算光线偏振度时,由于各参量之间的线性关系可以一定程度使这些误差相互抵消。 将两种偏振状态的仿真数据和实验数据进行归一化处理,如图8(b)和图9(b)所示,可以发现仿真数据和实验数据在偏振度随波长的变化趋势上保持一致。 对比水平线偏振光与右旋圆偏振光偏振度的幅值可以得到右旋圆偏振光的偏振度整体上高于水平线偏振光,但线偏振光的偏振度随着波长的增加呈上升趋势,圆偏振光的偏振度随着波长的增加呈下降趋势。

图9 (a) 右旋圆偏振光入射偏振度随波长的变化和(b) 归一化偏振度随波长变化
4 结 论
建立了单层组织模型,结合Rayleigh 和Mie散射模型采用Monte Carlo方法对生物组织的多光谱偏振特性进行了仿真和实验研究。 模拟了微粒尺寸为2 μm的生物组织在400~1 000 nm波段范围内的后向散射光的偏振特性,同时进行了实验验证,结果表明,圆偏振光的偏振度整体上高于线偏振光,但线偏振光的偏振度随着波长的增加呈上升趋势,圆偏振光的偏振度随着波长的增加呈下降趋势,这也揭示出圆偏振光在生物组织中具有更好的偏振保持性和更强的传播能力。 该研究明确了圆偏振光和线偏振光在生物组织中传输时的多光谱特性,为多光谱偏振生理信息获取提供了一定的理论参考。

