台风期间浮标和潜标上ADCP的空间变化、数据误差及校正

柯道勋，张 翰，唐佑民,5，左军成，许东峰，杨成浩，姚志雄，沈浙奇，田 娣

(1.河海大学海洋学院，江苏 南京 210098; 2.卫星海洋环境动力学国家重点实验室，浙江 杭州 310012;3.自然资源部第二海洋研究所，浙江 杭州 310012; 4.南方海洋科学与工程广东省实验室(珠海)，广东 珠海 519082; 5.北大不列颠大学环境科学与工程学院，大不列颠哥伦比亚，乔治王子城 V2N4Z9; 6.上海海洋大学海洋学院，上海 201306)

0 引言

声学多普勒流速剖面仪(Acoustic Doppler Current Profiler，ADCP)是一种测量流速的海洋声学仪器，主要通过回声的多普勒频移计算流速[1-2]。ADCP测量数据时会因自身系统和外部扰动出现误差。自身系统因素包括电子元件在水中的热噪音、波束相干和定位系统误差等[3]。唐华亮 等[4]发现ADCP相关幅值和良好率参数越高，测量数据的可信度越高。外部扰动包括周围环境的噪音污染、海表和海底的折射、波浪破碎及其加速度、悬浮物(浮游生物、沉积物、气泡等)散射和湍流压力等[5]。刘娜 等[6]发现生物附着使得ADCP测量盲区增大。CHEN et al[7]发现ADCP朝上观测时，表层数据精度较其他水层低一个数量级，原因是朝上观测时，声波受海-气界面的反射，回波信号偏大。针对ADCP数据的质量控制，已有一些方案：余军强 等[8]设计了ADCP流量测验辅助程序，可以在保障观测精度的同时提高观测效率；TRUMP et al[9]根据船底的GPS数据来校准ADCP的罗经，使罗经标准误差显著降低；CHIAO et al[10]利用一种基于多分辨率的三维插值法来提高模式数据的分辨率。

台风会引起上层海洋剧烈变化，如导致海表面波振幅显著增大[11-12]；导致海表水体辐散，引起局地上升流和后续的近惯性流[13-14]；改变混合和上升流等过程，影响上层海洋温盐结构[15-16]。同时，台风也会导致浮标、潜标系统上ADCP等仪器在水平和垂向上的位置发生较大改变，使测量数据产生误差。目前对走航ADCP观测资料的质量控制已有较多研究[17-18]，但对于台风等强扰动下浮标、潜标等观测系统上 ADCP 资料的误差和校正还缺少关注。

本文通过一套几何算法计算了台风前、后浮标和潜标上的ADCP空间变化和由此导致的流速误差，并进行相应的校正。通过台风期间观测系统上ADCP数据的质量控制，可以有效减小观测误差，提高数据的准确性，为分析海洋变化过程提供支撑。

1 数据介绍

1.1 浮标和潜标数据

浮标和潜标布放在南海北部，共设4个站位，各站均布放浮标和潜标两种观测系统，具体信息详见表1。

表1 浮标和潜标组成的布放站位信息Tab.1 Information of the deployed stations consisted in buoys and moorings

浮标投放时绳子采用“松弛”设计，即绳长大于水深，底部用重块固定。GPS安装在高度为4 m的浮标支架上，采样时间间隔为1 h。ADCP安装在浮标底部，高度为0 m，发射频率为150 kHz，向下采样，采样时间间隔为3 min，垂向分辨率为8 m，盲区为 14 m，厚层为232 m。

潜标系统处于水下，绳子通常处于绷紧状态，总长度小于水深，底部用重块固定。潜标上有2个 ADCP，都固定在同一个ADCP专用浮球上，分别进行向上和向下观测，发射频率分别为300 kHz 和 75 kHz，采样间隔分别为3 min和15 min，垂向分辨率分别为4 m和16 m，盲区分别为6 m和24 m，厚层分别为116 m和544 m。

1.2 台风数据

本文选取2014年台风海鸥(1415)进行研究，台风最佳路径数据集分别来自联合台风预警中心(Joint Typhoon Warning Center, JTWC)，中国气象厅(China Meteorological Agency，CMA)和日本气象厅(Japan Meteorological Agency，JMA)。JTWC、CMA和JMA数据的时间间隔均为6 h。

9月10日台风海鸥以热带低压的形式出现在帕劳岛附近，9月11日—14日向西北移动，移动过程中强度逐渐增强成台风，9月15日到达南海北部的4个观测站位，到达的时间、距离、移速等信息见表2。9月15日下午18时，海鸥的最大持续风速达到最大，为42 m/s，9月16日登陆，9月17日减弱为热带风暴并逐步消亡。

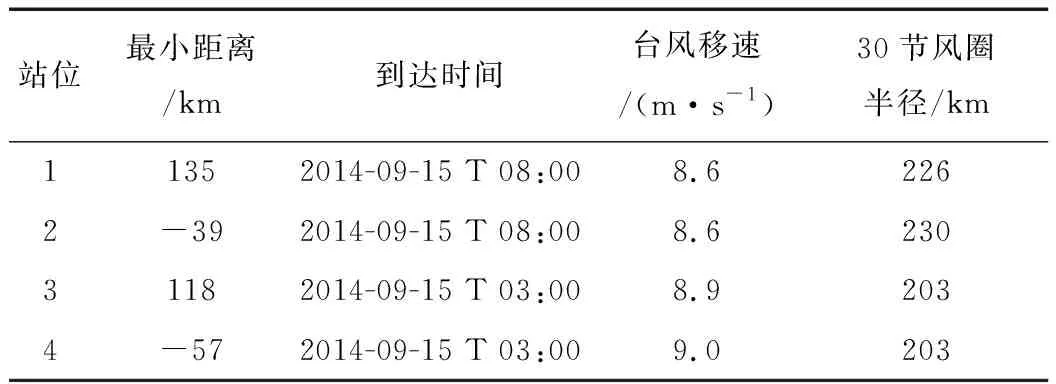
表2 台风到达观测站位时的相关参数Tab.2 Parameters of typhoon at the time reaching stations

2 台风期间ADCP数据处理方法

2.1 浮标上ADCP的空间变化、流速误差和数据校正

2.1.1 ADCP的水平位移

图1显示了浮标垂直和非垂直状态下ADCP的空间变化。垂直状态下ADCP的水平位移等于浮标系统的总绳长减去水深，即等于浮标多余绳子的长度。非垂直状态下浮标平台上ADCP的水平位移由浮标平台上GPS测的经度和纬度计算得出，计算公式为

(1)

(2)

Y(t)=2πr[latGPS(t)-lat0b]/360

(3)

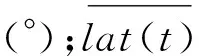
图1 垂直状态(a)及非垂直状态(b)下浮标系统上ADCP的空间变化Fig.1 Spatial variation of ADCP on buoy system in vertical stage (a) and non-vertical stage (b)

2.1.2 水平流速误差和水平校正

ADCP水平位移的变化会给流速测值带来误差。ADCP的水平流速误差为ADCP的水平移动速度，计算公式为

(4)

(5)

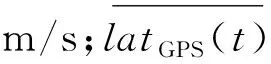
ADCP流速水平校正的目的是得出真实水平流速，即水平流速的校正值。浮标上水平流速校正值等于ADCP水平流速测值加上ADCP平移速度，其表达式为

(6)

式中：urb(t,z)、vrb(t,z)分别是纬向和经向流速的水平校正值，z表示水深；uob(t,z)和vob(t,z)是纬向和经向流速的测值。

2.1.3 垂向位移和垂向流速误差

浮标上的ADCP随波浪起伏产生垂向位移和垂向移速，垂向移速即为垂向流速的误差。垂向移速为垂向位移的时间导数，表达式为

(7)

Svb(t)=Hm(t)+D0

(8)

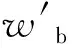
2.2 潜标上ADCP的空间变化、流速误差和数据校正

2.2.1 潜标上ADCP的空间变化

台风导致潜标ADCP发生空间变化，变化参数包括水平位移增量、垂向位移增量、ADCP相对于重块的水平位移和绳子倾角。位移增量反映ADCP在其观测深度范围内的运动状况。绳子倾角反映水平位移和垂向位移的比例，其中水平位移越大，倾角越大。

如图2所示，潜标ADCP位移增量可通过下式计算：

(9)

Dr(t)=max[D(t)]-min[D(t)]

(10)

dy(t)=D(t)-min[D(t)]

(11)

式中：dx(t)表示水平位移增量，单位为m；Dr(t)表示深度范围，单位为m；D(t)表示某时刻观测深度，单位为m；min[D(t)]表示最小观测深度，max[D(t)]表示最大观测深度，单位为m；dy(t)为ADCP的垂向位移增量，单位为m。从公式(9)可以看出，dx(t)随着dy(t)的增大而减小。当D(t)=max[D(t)]时，在公式(11)中dy(t)达到最大值Dr(t)，在公式(9)中 dx(t) 达到最小值0；当D(t)=min[D(t)]时，在公式(11)中dy(t)达到最小值0，在公式(9)中dx(t)达到最大值Dr(t)。垂直状态下，潜标ADCP深度与最小观测深度min[D(t)] 相等。

台风期间某一时刻仪器的垂向位移计算公式如下

Svm(t)=Ln+dy(t)

(12)

式中：Ln为垂直状态下ADCP到重块的距离，为常数，单位为m。

潜标上重块附近绳子倾角θ(t)的计算公式为

(13)

式中：Shm(t)为潜标的水平位移，单位为m。

2.2.2 潜标上流速误差和校正

潜标上的ADCP产生水平和垂向位移，导致流速测值在水平和垂直方向产生误差。潜标上ADCP的水平速度误差为

Uhm(t)=dShm(t)/dt

(14)

(15)

式中：Shm(t)为ADCP相对于重块的水平位移。

潜标上ADCP水平流速校正公式为

urm(t,z)=uom(t,z)+Uhm(t)sinθom(t)

(16)

vrm(t,z)=vom(t,z)+Uhm(t)cosθom(t)

(17)

式中：urm和vrm分别为纬向流速和经向流速校正值；uom和vom分别为纬向流速和经向流速测值；θom为ADCP测得的第一层流速的方向，正北方向为零。

潜标上ADCP的垂向移速为其垂向流速误差w′m，表达式如下

w′m(t)=dD(t)/dt

(18)

潜标上垂向流速的校正值wrm表达式如下

wrm=wom+w′m

(19)

式中：wom为ADCP垂向流速测值，单位为m/s。

图2 垂直状态(a)及非垂直状态(b)下潜标系统上ADCP的空间变化Fig.2 Spatial variation of ADCP on mooring system in vertical stage (a) and non-vertical stage (b)

2.2.3 潜标上ADCP的倾斜误差

图3所示为ADCP的结构和角度变化。如图所示，ADCP换能器发出声波的厚度由几十个深度单元组成，这个厚度称为厚层(Bin)，为设定常数，单位为m。当ADCP向下(上)观测时，观测剖面等于观测深度和厚层的和(差)。换能器与声波之间有一段距离没有声波覆盖，这段距离称为盲区(Blank)，为设定常数，单位为m。设定的盲区越大，ADCP换能器离测量水柱的距离越大，因此其测得的数据精度越高。ADCP 在测流的过程中会发生倾斜，影响其厚层在垂向上的投影，进而影响数据质量。倾斜校正是厚层投影到垂向上的过程，即对厚层Bin的校正，校正公式如下

Bin′(t)=Bincosθt(t)

(20)

式中：θt是ADCP倾角，Bin′是校正厚层。倾角θt的计算公式[19]为

θt(t)=sin-1[sinθp(t)sinθr(t)]

(21)

式中：纵摇(θp)是朝向在Y-Z面上的夹角(俯仰角)，横摇(θr)是朝向在X-Z面上的夹角(横滚角)(图3b)。由于换能器与主体成20°的夹角，因此当θp和θr大于20°时，认为ADCP测值无效。

图3 ADCP的结构(a)与纵摇和横摇(b)Fig.3 The structure (a), pitch and roll (b) of ADCP

3 台风期间ADCP数据处理结果

3.1 浮标ADCP数据的处理结果

3.1.1 ADCP的水平位移

浮标上ADCP的水平位移会给ADCP数据带来误差。图4为台风前后浮标的水平运动轨迹。浮标均围绕重块P(0，0)运动，其中1号浮标的轨迹形成2个小圆形(图4a)，2号～4号浮标的轨迹则形成1个大圆形(图4b～4d)。有两种方法可以确定重块的经纬度。第一种传统方法是以表1中站位的布放经纬度作为重块的经纬度；第二种方法是以GPS所测经度和纬度的中值作为重块的经纬度，这种方法称为中值法。采用传统方法结合公式(1～3)算出的1～4号浮标的最大水平位移(也称为水平位移半径)分别为4.9、6.3、5.88 和5.69 km，均超出了浮标挂绳的总长度4.5 km。由中值法结合公式(1)计算的最大水平位移半径分别为3.12、2.58、2.61和2.47 km，处于浮标总长度的范围内，因此中值法计算的最大水平位移更切合实际。

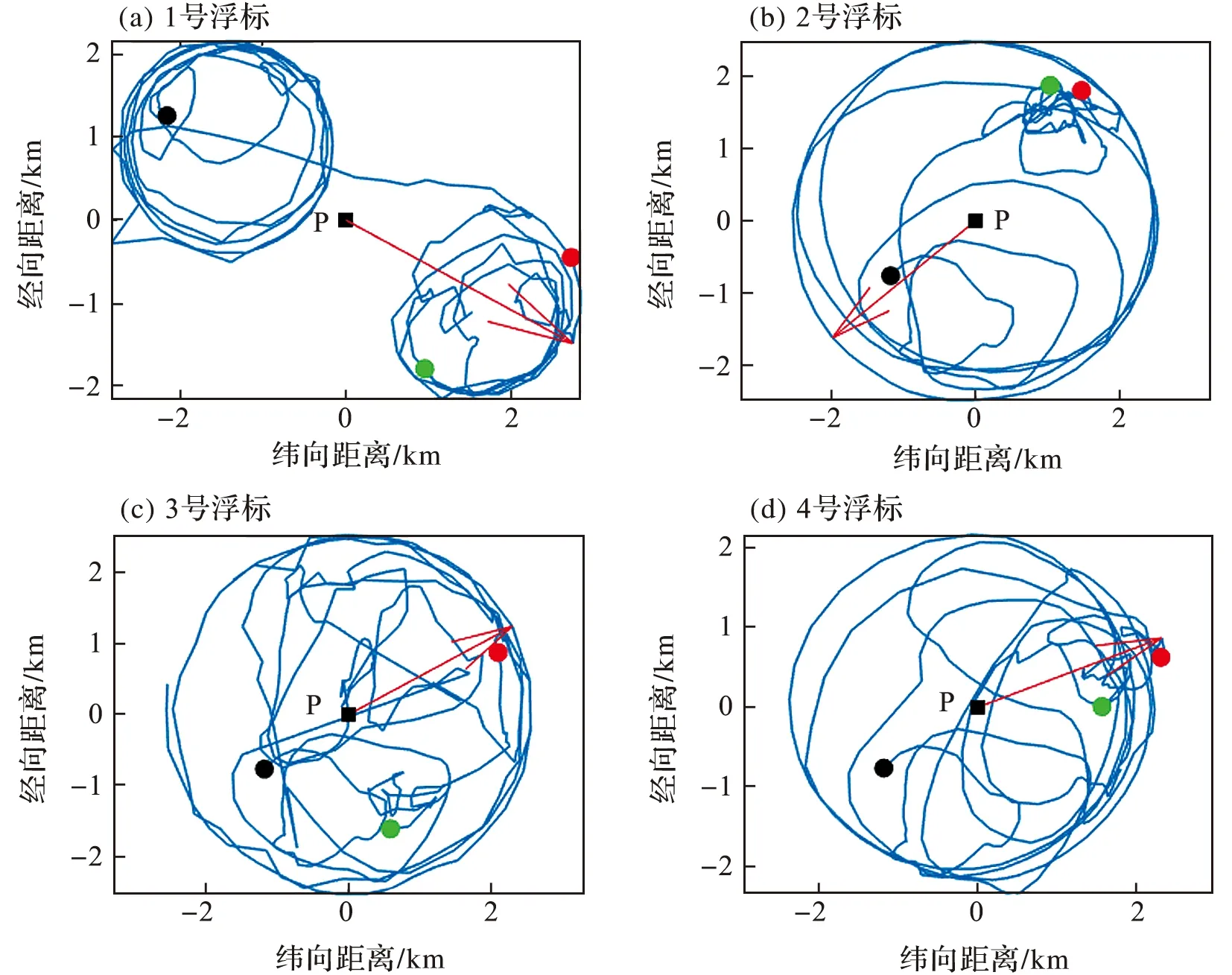
图4 各浮标的水平位移Fig.4 Horizontal displacements of each buoy

3.1.2 ADCP的水平流速误差以及水平校正

图5所示为浮标的水平移速，即ADCP的水平流速误差。由图可知，1号浮标水平流速的误差在台风前后都有周期性的变化。1～4号浮标上ADCP对应的水平流速误差最大值分别为0.20、0.27、0.21和 0.22 m/s。如图5b～5d所示，2～3号浮标的水平流速误差在台风过后的几天内均表现为大约1.5 d的近惯性周期运动，这反映了台风引起的近惯性流对浮标的推动作用。

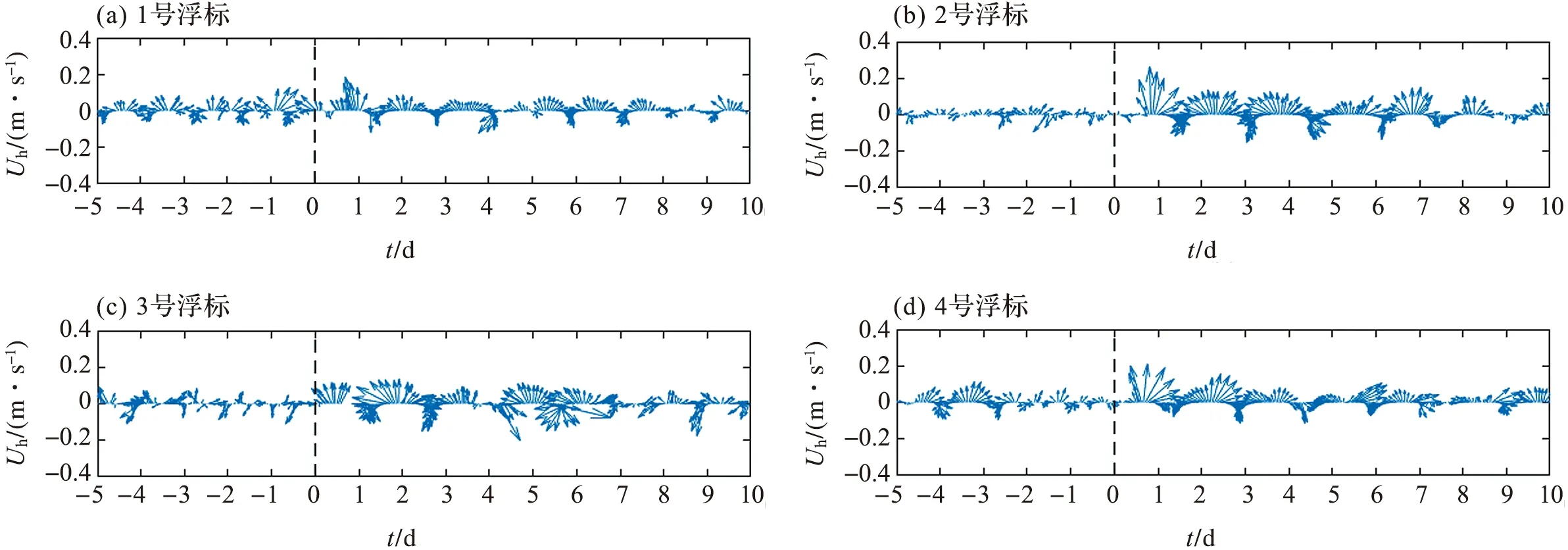
图5 各浮标上ADCP的水平流速误差矢量Fig.5 Horizontal velocity bias vectors of ADCP on each buoy

以2号浮标为例，比较水平校正前后浮标ADCP的水平流速。如图6所示，台风前，ADCP流速的水平校正值和测值差别不大。台风后，混合层(0～50 m)的流速水平校正值稍微大于测值，而温跃层(100～280 m)流速水平校正值显著大于测值(图6b中黑色方框内的流速)，这表明在台风过后对ADCP温跃层流速的水平校正非常有必要。

图6 2号浮标在混合层(a)和温跃层(b) ADCP水平流速的测值和校正值Fig.6 Observed value and correction value of horizontal speed in mixed layer (a) and thermocline (b) of ADCP on Buoy 2

3.1.3 浮标ADCP的垂向变化

台风后，各浮标处的最大波高显著增大，浮标上ADCP会有10余米的垂向位移。以1号浮标和3号浮标为例，台风后最大波高分别为18 m和 14 m，大约4 d后波高衰减成台风前的状态(图7a和7b)。垂向流速的误差如图7c和7d所示，在台风过后的1 d内，随着波高迅速增长，流速误差为正，但最大值仅为 5×10-4m/s；之后，随着波高逐渐降低，流速误差减小为负值，台风过去后4 d左右误差恢复至台风来之前的状态。4 d后的波高再增长来自后续热带气旋凤凰(1416)的影响，这里不再讨论。

图7 1号浮标和3号浮标处测量的最大波高及ADCP垂向流速误差Fig.7 Maximum wave height and vertical current velocity bias of ADCP on Buoy 1 and Buoy 3

3.2 潜标ADCP数据的处理结果

3.2.1 ADCP的空间变化

图8是潜标上ADCP的空间参数随时间的变化过程。1～4 号潜标上ADCP的垂向位移增量(dy)的最大值分别为32、179、133和152 m，ADCP相对于重块的水平位移(Shm)的最大值分别为916、1 501、1 332 和 1 354 m，绳子倾角(θ)的最大值分别为35°、24°、21°和22°。1号潜标上ADCP的水平位移增量在台风前2 d开始增大(图8a)，垂向位移增量开始减小(图8b)。2～4 号潜标上ADCP的水平位移增量在台风过后开始减小(图8e、8i和8m)，垂向位移增量开始增大(图8f、8j和8n)。1号潜标上ADCP的位移增量较小是因为其观测水深随时间的变化幅度较小。2号潜标上ADCP的位移增量较大是因为其离台风中心较近。

图8 各潜标上75 kHz ADCPs的空间参数Fig.8 Spatial parameters of 75 kHz ADCPs on each mooring

3.2.2 ADCP的水平流速误差

潜标上ADCP水平流速误差来自ADCP的水平移动。如图9所示，台风前后潜标上ADCP的水平流速误差变化不大，1～4 号潜标的水平流速误差的平均值和标准差分别为0.001±0.001、0.006±0.005、0.006±0.006和0.006±0.006 m/s。由于潜标上ADCP的水平流速误差相对于ADCP测值较小，因此这里不进行水平流速校正。

图9 各潜标上ADCP的水平流速误差Fig.9 Horizontal velocity bias of ADCPs on each mooring(正值/负值表示ADCP做远离/靠近重块运动。)(The positive/negative values represent that the ADCPs move away from/close to the concrete block.)

3.2.3 ADCP的垂向流速误差以及垂向校正

图10为2号潜标上ADCP的垂向流速误差以及垂向流速的校正值和测值。如图10a和10b所示，ADCP垂向流速误差的振幅在台风过后有轻微的增大，由于300 kHz ADCP和75 kHz ADCP安放位置相近且都在潜标上，因此垂向流速误差振幅接近。由于300 kHz ADCP观测的水层范围为温跃层 200～300 m，其垂向流速测值比垂向流速误差大一个数量级(图10c)，因此垂向校正后的流速与测值差别不大；75 kHz ADCP所测的水层范围为中层300～800 m，其垂向流速测值与垂向流速误差量级相同，因此垂向校正后的流速在台风过后的几天内显著增大，这说明垂向校正对中层流速的作用不可忽略。

图10 2号潜标上300 kHz和75 kHz ADCP的垂向流速误差、测值和校正值Fig.10 Vertical velocity bias, observed value and correction value of 300 kHz ADCP and 75 kHz ADCP on Mooring 2

3.2.4 ADCP的倾斜误差

如图11a所示，台风过后ADCP的纵摇和横摇增大。由于纵摇和横摇变化的幅度较小(变化范围在-5°～5°之间)，因此由公式(21)计算的 ADCP 倾角的量级更小(变化范围在-0.1°～0.1°之间，图11 b)，再由公式(20)可知，ADCP倾角对厚层的影响非常小，因此ADCP倾斜校正对数据的影响可以忽略。

图11 2号潜标上300 kHz ADCP的纵摇、横摇和倾角Fig.11 The pitch, roll and tilt angle of 300 kHz ADCP on Mooring 2

4 结论

本文基于2014年9月台风海鸥期间，南海北部的浮标和潜标上的声学多普勒流速剖面仪(ADCP)数据，提出了一套几何算法来计算台风过程中 ADCP 空间变化，并进行了误差分析以及相关的数据校正。计算结果显示：(1)浮标上ADCP水平位移可达 2.61 km，水平流速误差可达0.27 m/s，并在离台风较近的站位中出现近惯性振荡的信号；水平校正计算后发现，在台风过后的几天内混合层的流速变化不显著，而温跃层流速的水平校正值显著大于其测值；由于波浪的作用，浮标上ADCP的垂向位移可达10余米，但垂向流速误差较小，最大仅为5×10-4m/s，在垂向流速校正中可忽略。(2)台风导致潜标上ADCP的最大水平位移可达1.5 km，绳子倾角可达35°，ADCP 最大垂向位移可达179 m，由于近惯性波的作用ADCP空间参数具有近惯性 ；校正计算发现，潜标上ADCP的水平流速误差和倾斜误差均较小，可忽略不计，但垂向校正对台风过后几天内中层流速的作用不能忽略。

本文提出的ADCP数据质量控制方案能有效减小观测误差，更准确地反映海洋流场在极端情形(如台风期间)下的变化，可为更好地研究海洋变化过程服务。