HY-1C卫星运行轨道的计算研究

刘建阳，毛志华*,2,3,4，施 逸

(1.上海交通大学海洋学院，上海 200240； 2.卫星海洋环境动力学国家重点实验室，浙江 杭州 310012；3.自然资源部第二海洋研究所，浙江 杭州 310012； 4.南方海洋科学与工程广东省实验室(广州)，广东 广州 511458； 5.浙江大学海洋学院，浙江 舟山 316021)

0 引言

2018年9月7日，我国成功发射了海洋水色卫星HY-1C，用于探测全球水色、水温等，其在海洋污染、环境监测、海岸带动态监测等方面发挥着重要作用[1]。这些卫星产品数据需要经过资料处理才能获取，卫星轨道数据是资料处理过程涉及的重要参数，会直接影响卫星产品的质量，所以获取高质量HY-1C卫星产品数据离不开卫星运行轨道的高精度计算。在导航定位系统无法工作或接收导航信息有误的情况下，也可以利用搭载的算法继续进行轨道计算，提高HY-1C空间生存能力[2]。

刁宁辉 等[3]利用两行报(Two-Line Orbital Element，TLE)数据结合SGP4模型计算TERRA卫星轨道，并与STK(Satellite Tool Kit)模拟结果进行对比分析，位置和速度误差精度分别达到10 m和厘米每秒级别。刘卫 等[4]对SGP4/SDP4模型预报进行可靠性验证，分析出模型对低、中、高轨卫星预报误差的放大规律。韩蕾 等[5]利用SGP4模型实现了快速预测空间碎片轨道，初步评估的误差满足一定精度要求，SGP4模型避免了数值积分模型的初值精度要求高、运算速度慢等缺点。刘一帆[2]分析北美空防司令部NORAD双行元轨道预报模型，采用历元状态滤波建立了星上自主中长期轨道预报方法，并以太阳同步轨道卫星为例对算法进行仿真验证，算法精度满足要求。车通宇 等[6]采用SDP4模型、HPOP模型、历书星历3种方法对北斗导航卫星进行轨道预报，根据GFZ(Helmholtz-Centre Potsdam-German Research Centre for Geosciences)公布的精密星历评估3种预报：SDP4模型运算速度较快；预报3 d内的轨道，HPOP模型效果最好；预报时间超过3 d，SDP4模型精度更优。李征航 等[7]利用广播星历参数计算GPS卫星轨道，考虑摄动因素的影响，对计算的参数进行了摄动校正。

本文基于卫星轨道算法的研究现状，把轨道计算方法应用在HY-1C卫星上，并且通过比较2种算法的轨道误差，分析出摄动因素对轨道计算有很大的影响，在卫星运行轨道的高精度计算研究上具有一定的创新性。

1 数据与卫星轨道算法

1.1 两行报数据

两行报也称为卫星星历，是一种轨道编码方式，仅可以表述绕地飞行物体的轨道，由两行构成：第一行是描述卫星基本信息的7个参数；第二行是以轨道根数为主的9个参数，依次表示HY-1C卫星编号、轨道倾角i、升交点赤经Ω、轨道偏心率e、近地点角ω、平近点角M、当日绕地飞行圈数、发射至今飞行总圈数、校验位。HY-1C的两行报是本文研究卫星轨道算法的重要数据基础，下载自国家卫星海洋应用中心官方网站(http:∥www.nsoas.org.cn/)。

卫星轨道的6个基本参数定义如图1所示。图1a 中，OXYZ坐标系为地心惯性坐标系，X轴为地心指向春分点的方向矢量，P点为轨道近地点，S点为卫星位置，卫星轨道平面与赤道平面的夹角表示轨道倾角i，轨道升交点与春分点的地心夹角表示升交点赤经Ω，升交点与近地点的地心夹角表示近地点角ω。图1b 为轨道平面图，D点为地球，O点为椭圆中心，a、b分别为椭圆轨道的长半轴、短半轴，c为焦距的一半，c与a的比值表示轨道偏心率e；经过椭圆的近地点、远地点作虚线所示的辅助圆，经过S点垂直于长轴的直线交辅助圆于Q点，选取R点使得扇形POR与扇形PDQ的面积相等，则∠POR表示平近点角M。

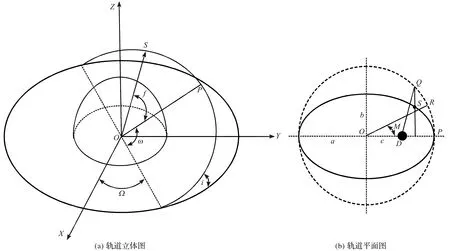
图1 HY-1C卫星轨道基本参数图示Fig.1 Diagram of HY-1C satellite orbit basic parameters

卫星运行轨道计算涉及的主要参数从两行报中提取，根据参考时间以及对应的轨道根数，使用合适的轨道算法模型可以计算出卫星在任意时刻的位置和速度。本文使用的是2021年8月1日的两行报，从该两行报中可以读取参考时间以及参考时间对应的轨道根数，两行报数据含义如表1所示。

表1 2021年8月1日HY-1C两行报数据含义Tab.1 The meanings of HY-1C TLE data on August 1, 2021

1.2 未考虑摄动的HY-1C卫星轨道算法

1.2.1 HY-1C卫星位置计算

本研究算法中HY-1C卫星位置的计算过程分为两步：第一步计算HY-1C在轨道平面的二维坐标，第二步计算HY-1C在WGS-84地心旋转坐标系下的三维坐标[8]，位置计算流程如图2所示。

图2 HY-1C卫星位置计算流程图Fig.2 Flow chart of HY-1C satellite position calculation

未考虑摄动力对卫星角速度的影响，则HY-1C卫星平均角速度为

(1)

式中：g为地球重力系数，a为卫星轨道长半轴。

对观测时间进行相对于参考时间的归一化处理，归一化时间记为tk。 HY-1C在辅助圆上的虚拟对应点R以平均角速度绕椭圆中心飞行，其与近地点之间的椭圆中心夹角表示平近点角，平近点角与时间呈线性相关，已知参考时间对应的平近点角为M0，则观测时间平近点角Mk为

Mk=M0+ntk

(2)

根据开普勒第二定律的推导[9]，偏近点角Ek与平近点角Mk满足公式(3)，当|Ek-Mk|>10-9时，运用公式(3)进行迭代计算，以此获得高精度的偏近点角Ek：

Ek=Mk+esin(Ek)

(3)

式中：e为两行报中的轨道偏心率。

用公式(4)和公式(5)联立成方程组，推导出真近点角fk，然后结合近地点角ω0计算观测时间的纬度幅角，即升交角距uk：

(4)

(5)

(6)

uk=fk+ω0

(7)

根据轨道长半轴a、轨道偏心率e、偏近点角Ek，计算观测时间径向rk，由几何关系可推导出径向rk在轨道平面系X、Y轴的分量，记为轨道平面的二维坐标(xk，yk)：

rk=a(1-ecosEk)

(8)

xk=rkcosuk

(9)

yk=rksinuk

(10)

Ω0e为参考时间对应的升交点赤经，tGAST表示最近星期日零点对应的格林尼治真恒星时(Greenwich Apparent Sidereal Time，GAST)，经过UTC(Universal Time Coordinated)时间转儒略日、儒略日转GAST两步转换而得。Ωe_dot为地球自转角速度，星历参考时间t0表示从最近的星期日零点到两行报参考时间所经历的秒数，则观测时间升交点赤经Ωk为

Ω0=Ω0e-tGAST

(11)

Ωk=Ω0-Ωe_dottk-Ωe_dott0

(12)

HY-1C卫星在地心旋转坐标系CGCS2000中的位置(Xk，Yk，Zk)为

Xk=xkcosΩk-ykcosiksinΩk

(13)

Yk=yksinΩk+ykcosiksinΩk

(14)

Zk=yksinik

(15)

式中：轨道倾角ik未考虑摄动校正，在数值上等于两行报中的轨道倾角。

对于从CGCS2000到WGS-84的坐标系变换，如果计算结果精度在厘米级别，则需要依次进行框架转换、历元转换、公式转换，最终实现CGCS2000坐标系与WGS-84坐标系的互换，否则二者不需进行转换，近似认为一致[10-11]。

1.2.2HY-1C卫星速度计算

结合位置计算中的参数，进一步计算出观测时间对应的偏近点角变化率Ek_dot、升交角距变化率uk_dot、径向变化率rk_dot以及升交点赤经变化率Ωk_dot：

(16)

(17)

rk_dot=aeEk_dotsin(Ek)

(18)

Ωk_dot=Ωdot-Ωe_dot

(19)

式中：Ωdot为参考时间对应的升交点赤经变化率。

则HY-1C在轨道平面系下的速度(xk_dot，yk_dot)为

xk_dot=rk_dotcosuk-rkuk_dotsinuk

(20)

yk_dot=rk_dotsinuk+rkuk_dotcosuk

(21)

在WGS-84坐标系中，观测时间对应的HY-1C卫星速度(Vk_X，Vk_Y，Vk_Z)为

Vk_X=xk_dotcosΩk-YkΩk_dot-
(yk_dotcosik-Zkik_dot)sinΩk

(22)

Vk_Y=xk_dotsinΩk+XkΩk_dot+
(yk_dotcosik-Zkik_dot)cosΩk

(23)

Vk_Z=yk_dotsinik+ykik_dotcosik

(24)

1.3 SGP4模型算法

Ken Cranford在1970年开发了适用于近地卫星的SGP4模型[12]，该模型简化了Lane和Cranford的广泛分析理论，首先从卫星变化的运动形式中计算平均运动的数值，用于确定卫星是近地运行还是深空运行，进而判断是否采用SGP4模型。SGP4模型适用于轨道周期小于225 min的近地卫星，HY-1C绕地周期约为100.4 min，可以使用该模型。

HY-1C卫星在太空中会受到各种摄动力的影响，其绕地运行不是简单的二体椭圆运动，SGP4模型考虑了地球非球形引力摄动、大气阻力摄动、日月引力摄动以及长短周期摄动项的影响[2-3,13]。为了减少各种摄动因素对卫星轨道的影响，需要对卫星所受的几个摄动力建立力学模型详细分析。地球引力模型采用BROUWER[14]在1959年提出的引力摄动解决方案；大气阻力模型与大气密度关系最密切，采用功率密度函数[15]；日月引力模型用于准确地计算出日月位置。

读取两行报数据，基于SGP4模型进行卫星轨道计算。首先初始化SGP4，设置始末时间和时间步长；其次利用SGP4模型计算出观测时刻惯性坐标系下的卫星轨道数据；最后根据格林尼治真恒星时进行地心惯性到地心旋转坐标系的转换。SGP4模型算法步骤：(1)计算卫星运行平均速度和轨道长半轴；(2)计算地球非球形引力和大气阻力摄动；(3)计算长周期摄动项；(4)计算短周期摄动项[2]。

2 结果验证

从2021年8月1日两行报中知悉“YYDDD”格式的参考时间为21213.33333333，与该时刻等价的UTC时刻为2021- 08- 01 08:00:00。用前文所述的两种算法计算HY-1C在各个观测时间对应的卫星位置和速度，观测时间从参考时间开始设置，以1 s时间步长进行递增，设置86 401个观测时间，共计24 h。最终呈现从 2021- 08- 01 08:00:00 UTC开始，至2021- 08- 02 08:00:00 UTC结束，以1 s时间步长递增，共计 86 401 个观测时间对应的86 401组HY-1C卫星位置、速度数据。

卫星轨道模拟最常用的仿真软件STK是由美国AGI公司开发的成熟系统分析软件，用于分析复杂的陆地、海洋、航天等任务，以及提供各种精确的分析报告和易于理解的图表[16]。STK的核心能力是生成位置、速度等数据，其复杂的轨道模型算法能够精确、迅速地确定任意时刻的卫星轨道数据，从而模拟出各种类型轨道。

使用STK 11.2.0版本软件，在STK软件中插入两行报文件，设置同样的时间步长与始末时间，共计 86 401 个观测时间点，进而模拟出24 h内卫星轨道数据。针对此时的卫星场景，先设置坐标系为地心地固坐标系，即WGS-84坐标系，然后导出星历表，从该星历表中提取卫星轨道数据作为参考标准[17]，用于与两种算法计算结果进行对比分析，验证误差精度。利用STK软件获取HY-1C卫星轨道参考数据的流程如图3所示。

图3 HY-1C卫星轨道参考数据获取流程图Fig.3 Acquisition flow chart of HY-1C satellite orbit reference data

2.1 未考虑摄动的算法验证

未考虑摄动因素的简便算法需要计算两个重要数据作为输入参数：参考时间与该GPS周开始时刻的间隔秒数，以及GPS周开始时刻对应的格林尼治真恒星时。GPS时间由GPS整周数以及GPS周秒数组成，每星期日零点作为每个GPS周开始时刻，两行报参考时间2021- 08- 01 08:00:00 UTC转化为从最近的星期日零点度量至参考时间的间隔秒数，作为星历参考时间，即参考时间与该GPS周开始时刻的间隔秒数。两行报参考时间对应的该GPS周开始时刻为2021- 08- 01 00:00:00 UTC，根据1.2.1节中的步骤即可转化为格林尼治真恒星时。

该方法计算的HY-1C卫星轨道数据与STK参考值相比，卫星位置误差如图4所示。横坐标表示观测时间与参考时间的间隔秒数，选择24 h内的观测时间进行比较，最大间隔秒数为86 400 s；纵坐标表示与参考值相比位置计算结果的误差；红、蓝、绿、黑曲线分别表示位置X误差、位置Y误差、位置Z误差及位置误差。从图可以看出，各位置分量误差较大，都近似呈正弦震荡趋势，位置X、Y误差振幅先增后减，依此循环，位置Z误差振幅逐渐增大。根据黑色曲线趋势可知随着观测时间的增加，HY-1C卫星轨道位置误差呈波浪形增加。如图5所示，24 h内的HY-1C速度误差同样较大，与位置误差变化趋势近乎一致，速度误差同样随时间推移而显著增加。

图4 24 h内未考虑摄动的HY-1C卫星位置误差Fig.4 Position errors of HY-1C satellite within 24 h without considering perturbation

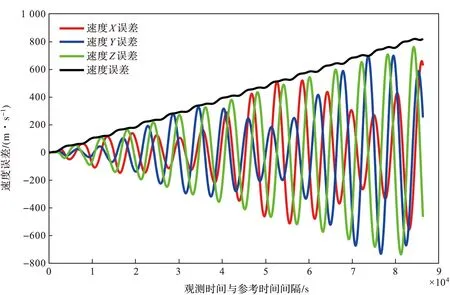
图5 24 h内未考虑摄动的HY-1C卫星速度误差Fig.5 Velocity errors of HY-1C satellite within 24 h without considering perturbation

选择1 h即3 600 s内的观测时间，将HY-1C卫星位置、速度的计算值与参考值进行比较，误差如 图6 所示。列举出观测时间从 2021- 08- 01 08:00:00 UTC开始到2021- 08- 01 08:30:00 UTC结束的16组HY-1C卫星轨道误差，时间间隔2 min，如表2所示，包括各个分量误差以及总误差。分析表2中误差数据可知0.5 h内的位置误差未超过10 km，速度误差未超过10 m/s。结合图6中0.5 h内误差曲线相对较为平缓的特征可知，未考虑摄动的简捷算法在短时间内可以进行轨道的粗略估计，轨道数据误差满足一定的精度要求。

表2 未考虑摄动的16组HY-1C卫星位置、速度误差Tab.2 16 sets of position and velocity errors of HY-1C satellite without considering perturbation

续表2

2.2 SGP4模型算法验证

SGP4模型算法计算的HY-1C卫星轨道数据与STK参考值相比，位置误差如图7所示。结合误差数据分析可知：24 h内HY-1C卫星位置误差未超过 68 m，误差很小，随着观测时间增加，位置误差总体呈震荡缓慢增大趋势；各分量误差也震荡缓慢增大，Z方向误差明显大于X、Y方向误差，Z方向误差小于65 m，X、Y方向误差小于32 m。速度误差如图8所示：24 h内HY-1C卫星速度误差很小，未超过 0.051 m/s，速度误差随观测时间增加总体呈震荡缓慢增大趋势。为了对轨道误差及其分量有直观的认识，统计24 h内前、后各10组观测时间对应的 HY-1C 位置、速度误差数据(表3和表4)，位置、速度误差均非常小，且总体呈缓慢增大趋势。

图6 1 h内未考虑摄动的HY-1C卫星位置、速度误差Fig.6 Position and velocity errors of HY-1C satellite within 1 h without considering perturbation

图7 24 h内HY-1C卫星SGP4模型位置误差Fig.7 SGP4 model position errors of HY-1C satellite within 24 h

图8 24 h内HY-1C卫星SGP4模型速度误差Fig.8 SGP4 model velocity errors of HY-1C satellite within 24 h

表3 HY-1C卫星前10组SGP4模型位置、速度误差Tab.3 The former 10 sets of SGP4 model position and velocity errors of HY-1C satellite

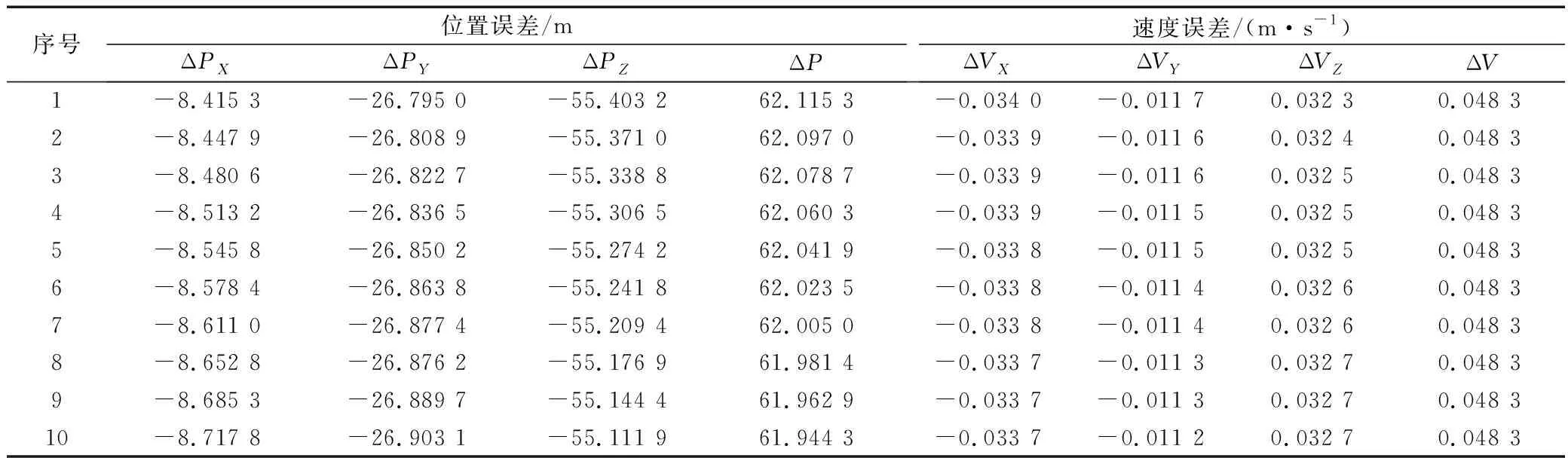
表4 HY-1C卫星后10组SGP4模型位置、速度误差Tab.4 The latter 10 sets of SGP4 model position and velocity errors of HY-1C satellite

3 误差影响分析

GPS、北斗等全球导航定位系统卫星轨道的计算方法中有一种是采用基于广播星历的公式法。根据参考时间的6个椭圆轨道根数以及3个长期项摄动参数和6个周期性摄动参数，计算卫星位置和速度，即对本文中第一种方法加以考虑摄动影响，对计算的各星历参数进行校正，最后计算的卫星位置精度可达10 m，卫星速度精度可达毫米每秒级别[18-19]。因此第一种方法是可行的，且考虑摄动因素时轨道计算误差很小，同时结合本文两种算法误差对比，可分析出影响HY-1C卫星轨道计算精度的因素。

第一，摄动因素的影响。HY-1C处在太阳同步轨道上，轨道倾角约为98.49°，离地面高度小于 1 000 km，属于近地卫星轨道。近地卫星轨道所处的高度较低，处在大气层的电离层中，会受大气阻力的干扰，大气摄动带来轨道衰退，甚至会影响卫星在轨时间；地球是个质量不均匀的椭球体，卫星轨道受地球非球形引力的摄动影响很大，如扁率引起的短周期摄动振幅可达数公里、引力场田谐调和项引起的短周期摄动振幅约半公里等[2]；同时还受到日月引力相对较小的影响。

第二，观测时间距参考时间越远，两种算法计算的卫星轨道数据误差也越大。从两行报中提取的轨道根数是针对参考时间而言，观测时间距参考时间越远，观测时间对应的轨道根数变化越大，相对而言，作为参考的两行报精度和可靠性就越差，即便对观测时间计算的星历参数进行校正，以参考时间轨道根数为基准的轨道计算误差也必然呈增大趋势。

4 结论

本文根据两行报数据，利用两种算法计算卫星轨道：一种是未考虑摄动的简便算法，另一种是SGP4模型算法。利用STK软件和两行报，模拟出真实卫星轨道数据即卫星位置、速度，作为参考标准与上述两种算法计算结果进行比较，以此验证算法精度，分析误差变化趋势以及重要影响因素，得出如下主要结论。

(1)未考虑摄动的算法在0.5 h内的位置和速度误差分别小于10 km和10 m/s，满足一定的精度要求，可以用于轨道的粗略估计；超过0.5 h，轨道误差随时间显著累加。

(2)SGP4模型算法精度非常高，24 h内位置误差小于68 m，速度误差小于0.051 m/s，可以用于HY-1C卫星轨道数据的精确计算。

(3)两种算法的卫星轨道计算误差都随观测时间的增加而震荡增大。

(4)摄动因素对卫星轨道精确计算有明显影响，建立各种摄动力数据模型可以准确地分析摄动因素对卫星运行的影响，减小轨道计算误差。