基于潮间带现场数据的底部切应力算法对比

孙剑雄,张文祥,史本伟

(华东师范大学河口海岸学国家重点实验室，上海 200241)

0 引言

底部切应力是泥沙起动、输运的主要驱动力，是水动力和泥沙输移模型中的关键参数。底部切应力的准确计算对河口海岸地区的泥沙输移、底床侵蚀淤积速率研究十分重要。通过直接测量法和理论公式计算法可得到底部切应力。直接测量法是通过测量应力板的形变量来获得底部切应力大小[1]，潮汐涨落变化引起的水面波动会使正压力发生改变，从而会影响应力板的测量精度。国内外学者将微型热敏式切应力仪应用到底部切应力的直接测量，并取得了一些突破[2-3]，但研究主要基于室内水槽实验。由于野外现场水体环境复杂，难以通过直接测量法获得准确的底部切应力，可通过测量水体底部边界层内脉动流速大小[4-6]结合公式计算底部切应力，理论公式有6种:(1)平均对数流速剖面法(Mean Log-profile Method, LP-mean)；(2)最大对数流速剖面法(Maximum Log-profile Method, LP-max)；(3)湍流动能法(Turbulent Kinetic energy Method, TKE)；(4)垂向湍流动能法(Modified Turbulent Kinetic energy Method, TKEW)；(5)雷诺应力法(Reynolds Stress Method, RS)；(6)惯性耗散法(Inertial Dissipation Method, ID)。每一种理论方法都是尽可能地简化了现场条件：LP-mean法和LP-max法需满足流速剖面在近底边界层内符合对数分布[7-9]；TKE法、TKEW法、RS法和ID法是根据湍流脉动流速来确定底部切应力[6,10-14]，因此和湍流紊动有关。与深水环境相比，真实浅水环境水动力条件复杂，波浪对水动力的影响显著，准确计算底部切应力很困难。前人虽已通过以上理论方法来计算底部切应力[6,15-16]，但应用这些方法计算河口海岸地区底部切应力时，不同方法的计算值差异较大。如魏东运[17]利用TKE法、TKEW法以及RS法分析了长江口水下20 m处因水动力引起的底部切应力，结果表明：长江水下三角洲和临近海域在空间上处于侵蚀的状态。该结论和前人的研究[18-19]结果明显不符。本文以苏北潮滩和崇明东滩等典型的浅水环境为例，先后布设了3个观测站点连续采集现场流速、波浪信息，应用6种理论方法分别计算底部切应力，对不同方法得出的结果进行对比与分析，以期选出相对适用于河口海岸潮间带浅水环境下底部切应力的公式。

1 数据与方法

1.1 样品采集与处理

江苏斗龙港地处长江口和废黄河口之间，面对着世界范围内非常独特的辐射沙脊群(图1a)。斗龙港现场观测站点为N，该地区属于不规则半日潮，多年平均潮差为2.42 m[20]，坡度平缓(仅为0.18‰～0.22‰)[21-22]，底床沉积物由50%以上的淤泥(中值粒径范围 8～63 μm)和 30%～40%的细砂混合物(中值粒径范围 63～125 μm)组成[21]。

图1 研究区域测站布设图Fig.1 Station layout map in study area

崇明东滩邻近东海(图1b)，同属于不规则半日潮，多年平均潮差为2.67 m，最大潮差为 4.6～6.0 m[23]，-5 m以上平均坡度为0.24‰。崇明东滩两侧以往复流为主，中部以旋转流为主，崇明东滩底床沉积物中值粒径为 10～45 μm[24]。向海方向植被带(海三棱藨草)与光滩分界明显。M1观测点布设在植被带与光滩的交界处，M2观测点布设在潮间带下半部光滩，M1与M2直线距离2 km。

在各观测站位直径3 m范围内现场采集5个 1 cm 层厚的底质样品进行均匀混合，室内利用激光粒度仪进行粒度分析，用于LP法计算底部剪切应力和临界侵蚀剪切应力。依据文献[25] 中的沉积物粒度测量前处理方法，在实验室内将现场采集的底质样品混合均匀后，称取0.5 g样品放置于试管内。向试管内加入质量分数为30%的过氧化氢(H2O2)，静置 24 h，去除样品中的有机质，将试管放入高速离心机(Avanti J-15)分离液体和固体颗粒(3 000 r/min，10 min)后倒出上清液。向试管内加入质量分数为 10% 的稀盐酸(HCL)，使其充分去除样品中的碳酸盐，静置24 h后，再次离心并倒去上清液。加入实验用超纯水对样品反复润洗至pH为7，再向试管内加入0.05 mol/L的六偏磷酸钠(NaPO3)6溶液并进行超声振荡5 min，用于分散样品颗粒。使用一次性塑料滴管吸取搅拌均匀的样品，加入到马尔文2000型激光粒度仪进样槽内进行分析测试。经过粒径分析测定，N测站、M1测站和M2测站的底质样品中值粒径分别为68.56、12.89和45.02 μm。

1.2 数据采集与处理

测量仪器安装在自制门型观测架上。声学三维高频流速仪ADV(Acoustic Doppler Velocimetry, Nortek,1～64 Hz)用于获取高频流速时间序列(包括水流的三维时均流速和脉动流速)，并记录探头距离底部床面的高度。波潮仪(RBR-wave, RBR, 1～16 Hz)用于获取波浪数据(包括有效波高、最大波高和有效波周期)和水深。数据采集信息、仪器布设高度以及参数设置如表1所示。

表1 数据采集信息以及仪器安装、设置详情Tab.1 Data collection information and instrument installation and setting information

由于ADV在测量过程中会受到仪器姿态、水体气泡以及湍流脉动强度等因素影响，数据的有效性需要进行分析与判断[26]。首先对ADV原始数据质量进行控制，剔除回声强度≤20 dB和相关系数≤70%的无效数据；其次采用相空间阈值法[27](Phase-space-thresholding, PST)寻找毛刺点并剔除，再根据前后数据进行多项式拟合替代毛刺点；最后进行滤波处理，采用正反傅立叶变换进行高通滤波，通过相位法分离波浪的影响。

1.3 底部切应力计算方法

底部切应力τc通过现场测量的平均流速和湍流脉动流速结合经验或者半经验公式计算获得，前人已经研究出多种利用现场流速数据计算底部切应力的理论方法。在本研究中，运用以下6种方法计算底部切应力。

1.3.1 平均对数流速剖面法(LP-mean)

对数流速法作为经典理论之一被广泛运用于计算底部切应力，该方法基于对数流速剖面的存在来计算底部切应力，假设垂线流速符合对数分布：

(1)

由于潮间带地区水深较浅，根据VOULGARIS et al[28]的研究对底部剪切应力进行水深校正：

(2)

式中：ub*为经过水深校正后的摩阻流速，h为研究区域的水深。

摩阻流速u*作为回归参数可以通过流速拟合求解，再根据公式(2)进行水深校正，切应力τc和经过水深校正后的摩阻流速ub*的表达式为

(3)

式中：ρ为流体密度。

1.3.2 最大对数流速剖面法(LP-max)

1.3.3 湍流动能法(TKE)

τc=Cρq

(4)

式中：C为常系数(C=0.19)；q为湍流动能，q=

1.3.4 垂向湍流动能法 (TKEW)

为了减小波浪轨道流速对TKE法计算底部切应力的影响，HUNTLEY et al[31]建议计算湍流动能q时使用受波浪轨道运动影响较小的垂向脉动流速w′，当仅使用垂向脉动分量计算底部切应力时，常系数C取值为0.9[6]。因此TKEW法计算公式为

(5)

1.3.5 雷诺应力法 (RS)

雷诺应力法计算公式为

(6)

式中：u′和w′分别为水平脉动流速分量和垂向脉动流速分量，上标“—”表示取其平均值。

1.3.6 惯性耗散法 (ID)

惯性耗散法是利用湍流脉动能谱估算湍流应力，最初是由DEACON[32]提出用于估算大气边界层的底部压力，后来被CHAMPAGNE et al[33]修正后用于河流及河口地区的研究。前人运用该方法对大陆架上的底部切应力进行了计算[31]。如果湍流能谱的测量是在恒定应力层内进行的，那么该方法行之有效。在对数层内，湍流动能的产生和耗散之间存在平衡，在惯性子区间内产生和消散的湍流能量的波数能被很好地分开，在该区间内没有能量的吸收和耗散，从低波数到高波数的能量通量就等于耗散率ε，三维惯性区间的能谱就表示为

(7)

式中：E(k)为波数谱，k表示惯性子区间内的波数，α为三维Kolmogorov常数。在惯性子区间内一维波数谱表示成：

(8)

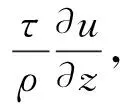
(9)

湍流的测量通常呈现出时间序列的形式，提供的是频率谱而不是波数谱。为了将波数谱转换成频率谱，需要引用泰勒“冻结湍流”理论[34]，该理论认为波数谱Øii(k)和频率谱Øii(f)存在下述关系：

(10)

摩阻流速u*的表达式为

(11)

式中：z为采样点距离底床高度，Øww(f)为垂向紊动频率谱，α3(≈0.68)为常系数。

按照公式(2)对摩阻流速u*进行水深校正，可以计算出底部切应力τc：

(12)

1.4 临界侵蚀剪切应力计算方法

临界侵蚀剪切应力作为底床沉积物起动的阈值，对判断沉积物是否起动有着指示性作用。GUO[35]提出了一种利用沉积物粒径计算临界侵蚀剪切应力τce的方法：

τce=τ*cD(γs-γ)

(13)

式中：τ*c为无量纲的临界剪切应力或临界希尔兹参数，γs为沉积物比重(取值2 650 N·m-3)，γ为水的比重(取值1 000 N·m-3)。

(14)

式中：D*为无量纲的沉积物直径；D为沉积物直径，单位：m；v为水的运动粘度系数(取值1.36×10-6m2·s-1)；g为重力加速度(取值9.81 m·s-2)；Δ为沉积物与水的比重之比(Δ=γs/γ)。

(15)

(16)

式中：R*c为颗粒临界雷诺数。

2 结果

2.1 斗龙港N测站

2018年6月26日—6月29日野外观测期间在N测站共采集到6个完整的涨落潮周期数据。该测站观测到最大水深为1.4 m，有效波高在 0.1～0.2 m之间，在各个潮周期内有效波高存在随着水深增大而增大的趋势，达到最大水深时有效波高值最大(图2a)。涨潮与落潮平均流速相当(≈0.15 m/s)(图2b)；u、v方向上的流速波动明显，u方向上的流速大小为 0～0.25 m/s，v方向上的流速大小为 0～0.2 m/s，w方向上的流速则较为稳定，为 0～0.002 4 m/s(图2c)。图2d～2i 为6种不同方法计算底部切应力的结果：LP-mean法切应力均值为 0.040 8～0.072 9 N/m2；LP-max法切应力均值为 0.356 7～0.572 9 N/m2；TKE法切应力均值为 0.596 1～1.037 1 N/m2；TKEW法切应力均值为 0.097 1～0.219 9 N/m2；RS法切应力均值为0.066 2～0.121 7 N/m2；ID法切应力均值为0.065 8～0.210 3 N/m2(表2)。N测站临界侵蚀剪切应力τce=0.160 0 N/m2，LP-max法和TKE法计算结果大于τce。在整个观测期间，N测站底部床面高度变化不大，T1潮周期内底床在缓慢淤积，淤积量在 4 mm 之内；T3潮周期后段以及T4潮周期底床在缓慢侵蚀，侵蚀量也在4 mm之内，底部床面高度较为稳定。

图2 江苏斗龙港N测站现场观测数据及剪切应力图Fig.2 Field observation data and shear stress diagram at N site in Doulong Port, Jiangsu Province

2.2 崇明东滩M1测站

2021年6月20日—6月22日野外观测期间在M1测站共采集到5个完整的涨落潮周期数据。该测站位于潮间带上部，淹没时间短、水深浅，观测到最大水深为1.1 m，有效波高主要处于0.05～0.24 m之间，与N测站观测到的波高数据基本一致，T2潮周期内有效波高较大，超过0.2 m(图3a)。M1测站平均流速小于N测站，整个观测期间平均流速变化范围小(<0.08 m/s)(图3b)；u、v方向上的流速小于N测点，u方向上的流速大小为0～0.15 m/s，v方向上的流速大小为0～0.05 m/s，w方向上的流速稳定，为 0～0.009 m/s(图3c)。图3d～3i为6种不同方法计算底部切应力的结果：LP-mean法底部切应力均值为0.005 3～0.018 1 N/m2；LP-max法底部切应力均值为0.469 8～0.945 8 N/m2；TKE法底部切应力均值为0.769 5～2.649 7 N/m2；TKEW法底部切应力均值为0.135 8～0.530 3 N/m2；RS法底部切应力均值为0.292 9～1.024 7 N/m2；ID法底部切应力均值为0.247 1～1.728 5 N/m2(表2)。M1测站平均流速小于N测站，但湍流脉动能量较高，LP-mean 法计算结果小于N测站，TKE法、TKEW法、RS法、ID法计算结果则高于N测站。M1测站临界侵蚀剪切应力τce=0.048 5 N/m2，远远小于N测站，除了LP-mean法计算结果小于τce之外，其余各方法计算结果均远大于τce。在整个观测期间，M1测站仪器探头距离底部床面高度稳定在278 mm，前后波动不超过4 mm。

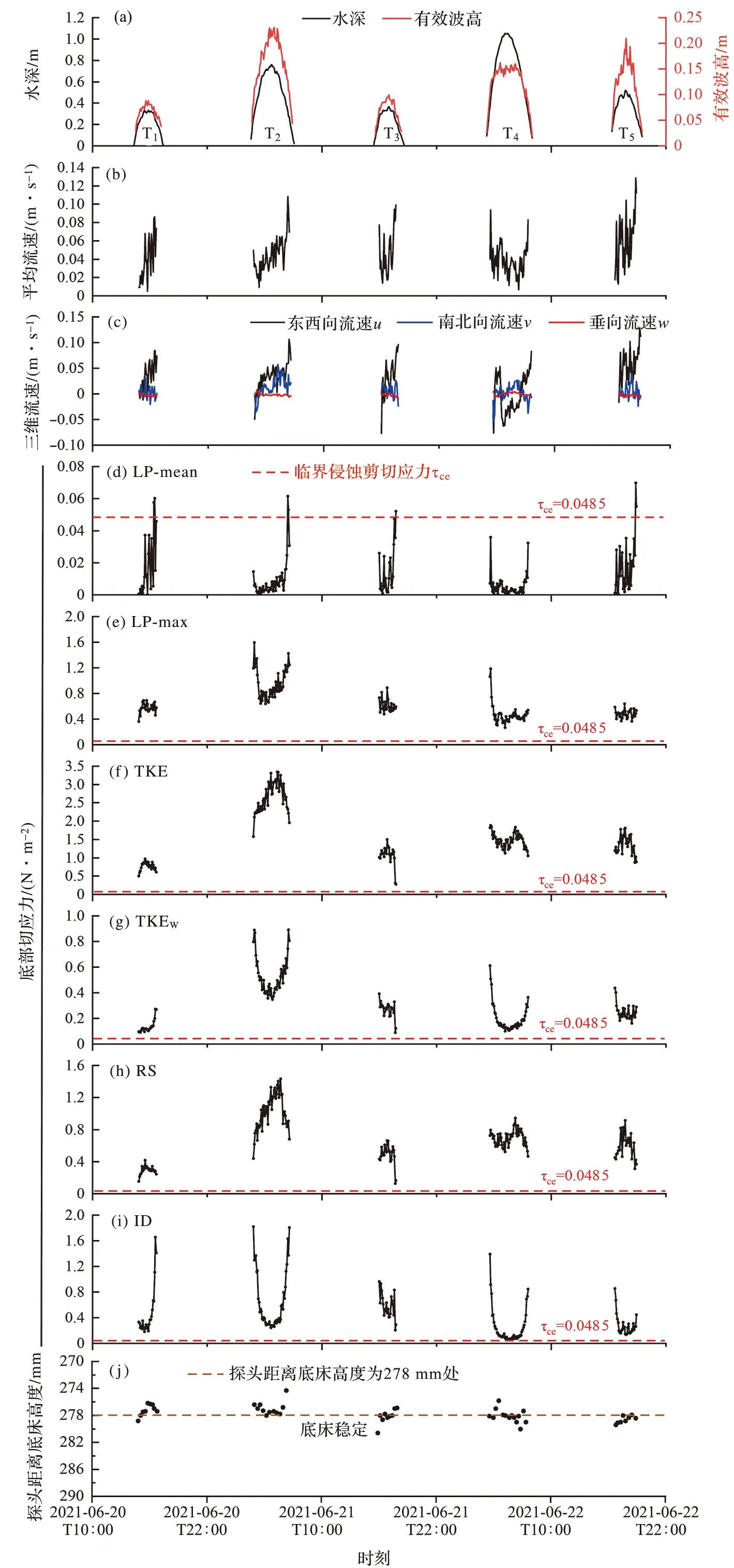
图3 崇明东滩M1测站现场观测数据及剪切应力图Fig.3 Field observation data and shear stress diagram at M1 site in the Eastern Chongming Shoal

2.3 崇明东滩M2测站

2021年7月26日—7月28日野外观测期间在M2测站共采集到4个完整的涨落潮周期数据。该测站位于潮间带下部，淹没时间长于M1测站、淹没水深更大，观测到最大水深为2.5 m，有效波高主要处于0.2～1.0 m之间，约为M1测站的4倍(图4a)。平均流速变化范围为0.3～0.7 m/s，约为M1测站的9倍(图4b)；u方向上的流速大小为0～0.4 m/s，v方向上的流速大小为0～0.6m/s，w方向上的流速稳定，为0～0.008 m/s(图4c)。图4d～4i为6种不同方法计算底部切应力的结果：LP-mean法底部切应力均值为 0.215 6～0.451 7 N/m2；LP-max法底部切应力均值为2.568 1～3.877 4 N/m2；TKE法底部切应力均值为9.971 2～14.148 6 N/m2；TKEW法底部切应力均值为1.404 5～2.752 4 N/m2；RS法底部切应力均值为0.785 0～2.476 0 N/m2；ID法底部切应力均值为 0.389 5～0.808 7 N/m2(表2)。M2测站平均流速以及湍流脉动能量远大于M1测站，各方法计算结果均大于M1测站，TKE法最大值甚至达到 24.909 0 N/m2。M2测站临界侵蚀剪切应力τce=0.127 4 N/m2，各方法计算结果均远大于τce。M2测站ADV未能记录到有效的底部床面高度变化数据。

图4 崇明东滩M2测站现场观测数据及剪切应力图Fig.4 Field observation data and shear stress diagram at M2 site in the Eastern Chongming Shoal

表2 各个潮周期底部切应力平均值Tab.2 Average values of bottom shear stress in different tide periods

3 讨论

本文利用6种理论方法计算底部切应力，其中LP-mean法是基于平均流速，LP-max法是基于最大瞬时流速，其余方法是基于湍流脉动(TKE法、TKEW法、RS法和ID法)。

M1测站底部床面较为稳定，除了LP-mean法之外，其余各方法计算结果均远大于临界侵蚀剪切应力τce。由于τce是通过沉积物粒径计算而来，其不仅与沉积物粒径有关，还与沉积物的形状、电化学性质以及湍流脉动相关[36]。M1测站沉积物中值粒径为 12.89 μm，属于黏性细颗粒，该测站τce计算值过小，不具备参考价值。在M1测站，LP-mean法相比其它方法而言，不能很好地估算底部切应力，计算结果和其它方法没有很好的相关性，计算的切应力比其它方法要低得多(表2)。SALEHI et al[10]利用LP-mean法同样也产生了较低的估值。从计算公式上分析，LP-mean法利用平均流速求解底部切应力，受控于平均流速的变化，尤其是 M1测站，平均流速变化仅为0.01～0.08 m/s，这是造成LP-mean法计算结果偏低的主要原因。此外，LP法与采样点距离底部床面高度z相关，理论上z不能够随着时间发生变化[12]，而实际上，潮间带底部床面高度是变化的。由SHI et al[37]实测潮间带底部床面高度变化可知，在一个潮周期内，底部床面高度的变化在厘米级，对于极端事件而言(如台风、风暴潮等)，底部床面高度变化甚至有可能达到10～20 cm。其次，LP法的应用需要假设流速呈现对数分布，但是现场流速状态并非如此，非稳定流、水体的层化、风应力加强后的波浪效应以及地形影响引起的二次流均会造成底部流速不符合对数分布。M1测站位于崇明东滩植被带与光滩交界处，植被带起到了缓流的作用，细颗粒沉积物容易在附近沉降，不仅会造成底部床面高程变化，还会影响底部边界层流速的对数分布规律。但是对于本研究中底部床面高度而言，M1测站底部床面前后变化稳定在4 mm之内，N测站底部床面侵蚀淤积总量在8 mm之内，对LP法计算影响有限。

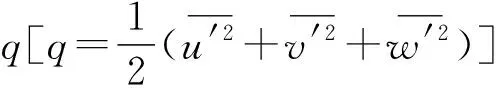
M2测站观测的有效波高最大，在所有观测潮周期内都能达到0.6 m，最高超过1.2 m。TKEW法采用受波浪影响较小的垂向脉动流速w′计算底部切应力，减小了波浪对计算结果的影响，在M2测站有效波高持续高于0.2 m的情况下，计算结果依然稳定。这与SALEHI et al[10]的研究发现一致，他们认为在有波浪的情况下，TKEW法是最合适的方法。N测站T4潮周期后半段底部床面缓慢侵蚀，TKEW法、RS法以及ID法计算结果在T4潮周期后半段均大于τce，在其它潮周期均略小于τce，符合底部床面高度变化规律。但是RS法在M2测站不适用，波浪作用会打破底部床面存在恒定应力层的假设条件。此外RS法对仪器探头的姿态较为敏感，在波浪和水流分别占主导地位时，仪器探头每1°的倾斜将分别导致156%和10%的误差[38]。M2测站的强烈波浪作用会引起仪器探头位置发生轻微偏移，可能会引起底部切应力结果误差。在较大波浪的环境下，ID法计算结果比RS法更加可信。HUNTLEY et al[31]利用ID法描述了加拿大大陆架底部切应力，认为在波流共存且水深条件充足的情况下，通过湍流波动谱来计算底部切应力是非常实用的。本研究得出了相近的结果，在水深充足的条件下，ID法计算结果不受有效波高波动的影响，计算结果十分稳定，不过在涨潮初期和落潮末期水深条件不足时，ID法计算结果偏大。总之，在潮间带浅水环境中底部切应力的计算存在着复杂性和不确定性，各方法在以波浪为主导的浅水环境中的应用还不尽完善。

4 结论

本文通过3个不同环境的野外站点获取现场观测数据，根据6种不同的理论方法计算底部切应力并进行对比与分析，主要结论如下。

(1)潮间带浅水环境条件复杂，受到平均流速、仪器探头距离底部床面高度以及波浪强弱变化的影响，LP-mean法会低估底部切应力。

(2)潮间带浅水环境波浪作用明显，流速变化幅度较大，LP-max法和TKE法会高估底部切应力。

(3)通过对TKE法进行改进，TKEW法利用受波浪影响较小的垂向脉动流速计算底部切应力，更适用于波浪作用强烈环境下底部切应力的计算。

(4)波浪作用会造成RS法计算结果产生误差，存在较大波浪时，ID法计算结果比RS法计算结果更加可信，但是在水深条件不足时，ID法会高估底部切应力。

本文只对3个不同环境潮间带浅水区域底部切应力进行了研究，对于近岸河口区以及潮下带区域，由于受水深、流速、波浪等多种因素的影响，不同方法计算结果会产生差异，各种理论方法在不同环境中的适应性还有待进一步研究。